“双创”背景下“高等数学”课程中旋转体体积可视化教学设计
宣晶雪 张权
齐齐哈尔大学理学院 黑龙江齐齐哈尔 161006
随着科技的发展和社会的进步,“双创”教育已成为教育改革的必然趋势[1]。为满足社会需求,我国愈加注重创新战略型人才的培养。全国各高等院校积极响应,高校教师纷纷推进“双创”理念融入课堂的工作。“双创”教育即为创新和创业教育[2]。旨在高等教育教学环节的主渠道中,以基础理论知识为载体,恰当合理地在日常教学中融入“创新创业”理念,加强培养青年学子科技创新实践的能力,推动其积极加入社会各项实践活动,获取创业知识与经验。促使青年学子基础理论知识与创新实践能力协同并肩,促进其蓬勃发展。
“高等数学”作为各高校理工科类别的一门既基础又重要的理论课程,具有理论知识冗杂繁多、概念抽象难以理解、逻辑思维需求较高的特点[3]。除此之外,“高等数学”学科更善于传授理论基础,对创新能力的培养与创业知识的传播并不透彻。所以,这就需要高校教师们对现有的教学模式进行改革,将“双创”教育理念合理恰当地融入教学工作中,深度培养并锻炼青年学子的创新能力,鼓励其积极创业。
将“双创”教育理念合理恰当地融入“高等数学”日常教学中,青年学子们无疑是最大获益者。一方面保证了教育资源多样性、教育方式多元化、教育模式生动化、教学内容印象化,在学科知识体系的基础上,理论联系实际,结合创新创业理念进行拓展,促使青年学子在大脑皮层留下深刻的印记,有效激发学习兴趣。另一方面,“双创”教育理念在传播给青年学子创新意识、创业知识的同时,也在一定程度上推动其逻辑思维能力的发展。在科研知识创新探索过程中,青年学子逐步形成缜密的逻辑思维,保持良好的自主探究能力和独立思考问题的习惯,培养其多方位、多元化、多维度看待事情。“高等数学”作为理工科类别必不可少的专业基础学科,旨在培养思维方式多元化、思想品德高尚化、创新能力科研化的战略型人才。所以在教学过程中,教师要将学生放在教育的主体地位上[4],充分探索学生的主动性。根据课程内容合理布置思考问题,引导学生用创新的理念解决问题,注重强化学生的创新意识,锻炼其创新能力。教学方式也要多样化,可根据课程需要通过多媒体展示知识内容[5],尤其是视频图例等,能够直观清晰展示课程内容。开设多样的实践活动,培养青年学子动手动脑能力,师生共同探究,教学相长。考核方式多元化发展,可在平台多设置探究活动,并记录成绩作为考核的一部分,在教学考核中无形促进其创新意识的养成与能力的提升。
1 课程目标
1.1 知识目标
(1)理解与掌握薄片法与柱壳法的方法和思想。
(2)熟练掌握绕x轴,绕y轴旋转体的体积公式。
1.2 能力目标
(1)通过可视化培养学生空间架构想象能力;通过薄片法、柱壳法探究培养学生逻辑推理的能力;通过概念知识讲授培养学生领悟理解能力。
(2)通过小组讨论培养学生自主学习、团结合作、善于观察总结、乐于探索的能力。
1.3 情感目标
(1)通过引入神舟飞船视频,培养学生乐于奉献、科技强军、航天报国的爱国主义情怀。
(2)通过问题探究培养学生勤于动脑,善于思考,从多维角度看待问题的态度。
2 教学过程设计
2.1 问题探究
多媒体展示旋转体图片,神舟飞船视频以及雷达卫星图片并设置思考问题:(1)它们都是怎样的几何体?(2)何为旋转体?
引导学生分小组自主探究并查阅相关资料,了解旋转体的定义,并以小组为单位进行汇报。
探究结果汇报:
旋转体定义:旋转体是由一个平面图形或是一条平面内的曲线,围绕着平面内任何一条直线旋转一周而形成的几何体,平面内这条直线就称之为旋转轴[6]。
以动画形式直观演示矩形、直角三角形、直角梯形绕其一条直角边旋转一周而成的旋转体,如图1所示。并计算其旋转体体积。

图1 旋转体展示图
(1)矩形围绕其一条直角边旋转一周所形成的旋转体称之为圆柱体,圆柱的体积为:V圆柱=底面积×高。


进行总结,并设置问题:圆柱、圆锥和圆台都是中学学过的规则的体,所以它们的体积容易计算。那么,如果是曲边梯形围绕坐标轴旋转一周所形成的不规则的体,其体积应该如何计算?
2.2 重难点探究与分析
给出具体问题案例,设置问题探究,引导学生分小组讨论。
2.2.1薄片法
设曲线y=f(x)是一条连续的曲线,且f(x)≥0,现有一个曲边梯形,由曲线y=f(x),x=a,x=b以及y=0所围成,现令这个曲边梯形绕x轴旋转一周[4],其所形成的不规则旋转体的体积应如何计算?
图2为可视化曲边梯形图片,提示学生采用微元法的方式来计算,并引导学生回顾微元法思想和计算方法,其具体思想是化“不规则”为“规则”。

图2 薄片法旋转体图
探究结果检验:
①分割:在区间[a,b]上任意插入n-1个分点,记a=x0,x1,x2…xn-1,xn=b,则区间[a,b]被分成n个大小相等的小区间,并记做[x0,x1],[x1,x2]…[xn-1,xn],并令xi-xi-1=dx(0≤i≤n)。
②近似替代:取任意一个小区间[x,x+dx],其中dx是非常微小的量,对于窄曲边梯形ABCE而言,可近似用窄矩形ABCD替代。窄矩形ABCD绕x轴旋转一周所形成的旋转体为圆柱体。圆柱体中的高即为[x,x+dx]的区间长度dx,圆柱体的底面半径为x点处对应的函数值f(x)。那么,圆柱体的体积等于底面积×高,即为πf(x)2dx,即小区间[x,x+dx]所对应的体积微元dv为dv=πf(x)2dx。

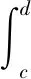
例1:计算由曲线y2=x且x∈[0,1]与y=0所围成的曲边梯形分别绕x轴y轴各旋转一周所形成的旋转体体积。
图3为可视化曲边梯形形状,直观演示其分别绕x轴,y轴旋转而成的旋转体。并引导学生回顾根据薄片法得到的绕x轴和绕y轴旋转体的体积公式。


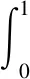
根据牛顿——莱布尼茨公式求解上式,得:
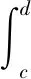
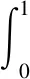
根据牛顿——莱布尼茨公式求解上式,得:
2.2.2柱壳法
设置问题,引导学生分小组探究:仍是上述曲边梯形,由曲线y=f(x)(f(x)≥0),x=a,x=b以及y=0所围成,现令其绕y轴旋转一周,所形成的不规则旋转体的体积应如何计算?
图4为柱壳法对应旋转体演示过程图。以小组汇报的形式,鼓励学生创新探究,检验探究结果,并计入考核成绩。通过可视化的方式,引导学生共同分析汇报内容如下:

(a)

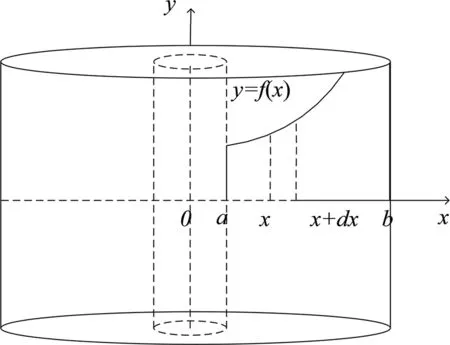
图5 柱壳法旋转体图
例1中曲线y2=x且x∈[0,1]与y=0所围成的曲边梯形绕y轴旋转一周所形成的旋转体体积可采用柱壳法方法计算。

根据牛顿——莱布尼茨公式求解上式,得:

2.3 总结归纳
通过引导青年学子以共同回忆的方式来梳理旋求转体体积的知识脉络,进行归纳总结,使青年学子清晰直观地掌握课程核心内容。
3 课后检验
通过探究式的自主学习过程,以及对旋转体体积公式的掌握,完成布置的课后任务,并在规定时间内提交,完成布置的知识测评。
4 课程思考拓展
(1)寻找生活中旋转体的案例,例如圆形水杯、椭圆形的橄榄球等,并尝试是否能计算出其体积?
(2)布置思考任务:若某立体不是旋转体,但该立体垂直于某一定轴的各个截面面积AX已知[6],则该立方体的体积应如何来计算?
“高等数学”这门学科不单单传授给学生科学文化知识,更要锻炼学生逻辑思维能力,培养学生良好的创新意识和高尚的道德情操。本文基于“双创”背景下,以“高等数学”课程中求旋转体体积为例进行教学设计。摒弃传统教学模式,对讲授方法与讲授内容进行革新。借助于多媒体渠道,通过“探究式+可视化”的教学方式,分别介绍了薄片法、柱壳法以及其分别对应的绕x轴,y轴的旋转体体积公式。数形结合的可视化让学生直观感受到旋转体空间立体构架,更易接受并理解深刻。分小组探究讨论充分发挥了青年学子自主式学习,提升其学习热情与积极性。积极探索课程教育学新领域,这种教育革新更适应社会需求,保证了“双创”教育理念下创新型战略人才的培养与快速发展,在一定程度上推动了“高等数学”课堂教学质量的提升。

