隐函数求导数的五种方法
张亚龙 高改芸 刘爽
北京科技大学天津学院 天津 301830
隐函数求导数是多元函数微分法应用的重要内容之一,也是高等数学中的一个难点。利用多元复合函数求偏导,对于初学者容易出错。利用隐函数求导数可以求解空间曲线的切线与法平面、空间曲面的切平面与法线和多元函数的极值、最值等。将一元函数求导数和多元复合函数求偏导数的方法,应用到求隐函数导数中。高等数学的教材中只给出了公式法求多元隐函数导数,本文总结出五种方法求隐函数导数,这样面对隐函数求导问题时,我们可以选择较多方法求解,便于对隐函数求导数的应用。
一、隐函数存在定理
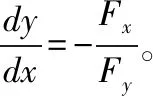
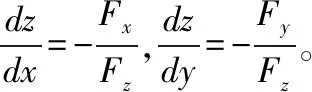
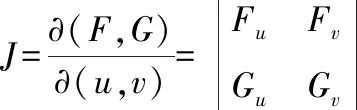
二、一个方程确定的一元隐函数和二元隐函数求导
(一)显化法
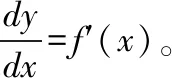
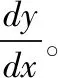

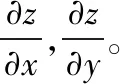
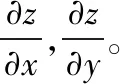
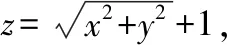
说明:利用显化法求隐函数的导数,要求给定的方程可以显化,即自变量与因变量可分离,但对于绝大部分情况是难以显化或无法显化的,如由方程ez-xyz=0确定的隐函数,此时显化法失效。
(二)直接法

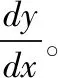
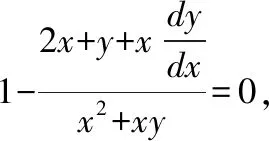
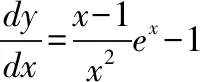
将直接法推广到二元隐函数中,设方程F(x,y,z)=0,确定的隐函数z=f(x,y),对方程两边直接关于自变量x或y求导,此时z是x,y的函数,求偏导数时,需要把z看作x,y的函数。
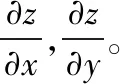
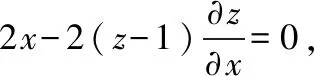


(三)公式法
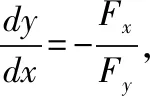
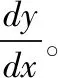
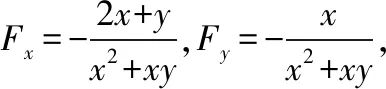

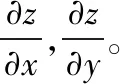
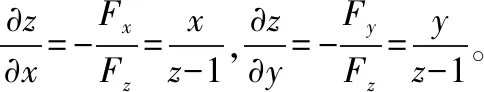
说明:公式法首先需要令函数F(x,y)或F(x,y,z),不需要考虑函数之间的复合情况,只需熟记公式,只要将F看成x,y或x,y,z的函数,对其求偏导数。而直接法需要弄清楚各变量的复合情况,进行复合函数求偏导,难度相对于求简单的偏导数有所提升,但直接法的解题思路非常重要,可用于求解隐函数组导数。
(四)微分法
设方程F(x,y)=0,确定函数y=f(x),利用微分形式不变性,对方程两边同时求微分,此时需要将F看成关于x,y的一个二元函数。
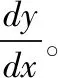
设方程F(x,y,z)=0,确定隐函数z=f(x,y),利用全微分形式不变性和全微分的叠加原理,对方程两边同时求全微分,此时需要将F看成关于x,y,z的一个三元函数。
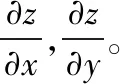
说明:不难看出,全微分法求偏导数时,需要熟练应用微分运算法则与全微分形式不变性。实际中,大部分读者不善于用全微分形式不变性求解,通过求解上题,用微分法求解过程简单,与显化法、直接法相比较,建议使用微分法求解。
(五)对数求导法
对于某些隐函数求导的问题,直接用上述四种方法求解时,过程相对复杂,此时需要在方程的两边同时取对数,然后利用复合函数求偏导法则求出隐函数导数,这种方法称为对数求导法。一般适用于当方程中含有幂指函数的项的情形。
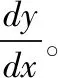
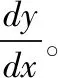

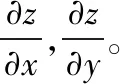
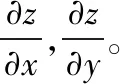
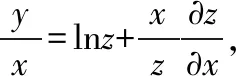
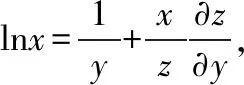
说明:例8和例9都是先对方程两边同时取对数,然后利用直接法求解。实际中,也可以取对数之后,然后在两边取微分,利用微分法求解。方程两边同时取对数的目的是为了求导简单,本质上我们还是需要利用直接法或微分法求解。
三、方程组确定的一元隐函数和二元隐函数求导
设方程F(x,y,z)=0,G(x,y,z)=0,确定的一元隐函数为y=y(x),z=z(x),下面分别利用直接法、公式法和微分法求解此类隐函数导数。
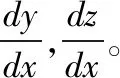
解1 直接法
方程组两边同时对x求偏导,得:
即:
则:
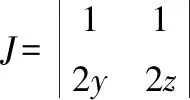
所以:
解2 公式法
令F(x,y,z)=x+y+z,G(x,y,z)=x2+y2+z2,分别对F,G求关于x,y,z的偏导数,得Fx、Fy、Fz与Gx、Gy、Gz,进而得出:
代入公式,得:
解3 微分法
说明:通过例11的三种解法,我们不难发现,对于由方程组确定的一元隐函数,利用微分法求解,优点突出,可以有效地避开函数各个变量之间的复合关系,将每个变量都看成自变量,求微分即可。公式法需要记忆公式,但是由方程组确定的隐函数公式相当复杂,无论对教师还是学生优先使用微分法,次之使用直接法与公式法。
设方程F(x,y,u,v)=0,G(x,y,u,v)=0,确定的二元隐函数为u=u(x,y),v=v(x,y),同样利用直接法、公式法和全微分法求解此类隐函数导数。

解1 直接法
方程组两边同时对x求偏导,得:
即:
则:
所以:
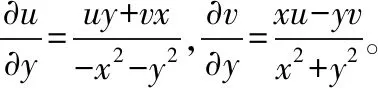
解2 公式法
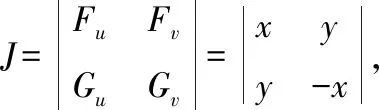
解3 全微分法
对两个方程两边同时求全微分,得:

整理得:
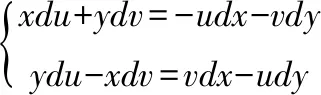
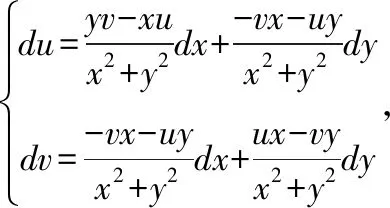
说明:通过例12的解题过程,不难发现全微分法优势更加突出,对于解方程的过程也相对简单。公式法需要记忆公式,直接法需要解两次方程组,而且在求偏导数时容易出错,因此全微分法最简单。
通过对一个方程确定的隐函数求导和方程组确定的隐函数组求导对比,利用直接法、公式法、微分法三者的计算量和复杂程度区别不是很明显。但是对于方程组确定的隐函数来说,微分法优势突出,过程比直接法与公式法简单,计算量小,不管函数和自变量如何变化,各变量之间的复合情况,始终将函数和自变量同等地位处理,从而提高正确率。
结语
本文给出求隐函数导数的五种方法,不仅可以解决一元隐函数求导问题,同时也适合于多元隐函数求导,对于在求解的过程中,每个方法都有优缺点。显化法、直接法、微分法、对数求导法都不需要记公式,但显化法要求给定的方程可以显化,对于很多方程是不可以或者不容易显化的,所以对于隐函数求偏导,一般情况下不使用显化后再求偏导数的方法。直接法需要知道函数中各个变量的复合情况,明确各变量之间的关系,利用复合函数求偏导计算隐函数的导数,容易出现错误,但是直接法的适用性很强,因此也会被广泛应用,并且公式法可以由直接法推得。公式法需要构造函数F(x,y)或F(x,y,z),对函数F(x,y)或F(x,y,z)求偏导数即可,此时需要将F看作x,y或x,y,z的函数。计算过程简单,但需要熟记公式。微分法不需要关心变量之间的关系,利用微分叠加原理和全微分不变性,对方程两边求全微分。微分法求隐函数导数是一种简单、易懂的方法,且不容易出错。对数求导法需要方程中含有幂指函数的形式,局限性比较大,但计算过程相对简单。
对于由方程组确定的隐函数,全微分法优点更突出,既不需要记忆复杂公式,也不需要考虑函数变量之间的复合关系,以不变应万变,通俗易懂,直接利用微分形式不变性求解隐函数导数。因此,无论是方程还是方程组确定的隐函数,利用微分法最简单。实际中,大部分学生没有利用微分法求解隐函数导数,所以教师应在高等数学课堂上对全微分法进行重点讲解与应用,使学生能够熟练应用微分法求解隐函数导数,让求隐函数导数不再是高等数学中的一个难点问题。

