可解译深度网络的多光谱遥感图像融合

余典，李坤，张玮，李对对，田昕*，江昊

1.武汉大学电子信息学院，武汉 430072; 2.中国资源卫星应用中心，北京 100094

0 引 言

受限于传感器光学系统设计的局限性，遥感图像空间分辨率和光谱分辨率之间存在相互约束的关系。例如，多光谱图像(multispectral image, MSI)具有较高的光谱分辨率和较低的空间分辨率，而全色图像(panchromatic image, PAN)则具有较高的空间分辨率和单一光谱信息。多光谱图像融合，又称Pansharpening，将同一时区、同一目标的低空间分辨率MSI和高空间分辨率PAN，按照一定算法进行信息提取和运算结合，可以融合生成高空间分辨率的MSI，从而在光谱特性和空间结构方面均可以达到对成像目标更为准确地识别，极大提升了定量分析的精度和可靠性。近半个世纪以来，多光谱图像融合可在同时搭载MSI和PAN的遥感卫星中直接应用(如IKONOS、QuickBird、Gaofen-2等)，在自然灾害监测、军事侦探、土地测量和农业分析等多个领域发挥出巨大应用价值(王海荣 等，2021；Pohl和van Genderen，1998；焦姣和吴玲达，2019)。

1 相关工作

目前代表性的多光谱图像融合方法主要包括：成分替换方法(component substitution, CS), 多分辨率分析方法(multi-resolution analysis, MRA)、变分模型优化方法(variational model optimization, VO)以及深度学习方法(deep learning, DL)(胡鑫，2021)。CS方法首先通过矩阵分解将MSI分离出空间和光谱信息，进一步将PAN与MSI的空间信息叠加后进行相应逆变换得到融合MSI。Tu等人(2001)首先提出了一种基于IHS(intensity hue-saturation)空间映射的多光谱图像融合的方法。进一步地，非线性IHS变换(Ghahremani和Ghassemian，2016)和非线性主成分分析(principle component analysis, PCA)变换(Licciardi等，2012)分别用于成分替换，从而有效提升融合性能。虽然CS方法可以有效增强空间细节，但是往往存在较强的光谱失真。MRA方法则是通过对MSI和PAN进行多尺度分解，在不同尺度下融合相应的分解系数以得到融合图像。例如，采用非下采样轮廓基函数方法进行多尺度分解，克服了小波基下采样过程中带来的失真问题(da Cunha等，2006)。其他常用的多尺度分解方法包括Laplacian金字塔分解方法(Do和Vetterli，2002)、Morphological filter方法(Aiazzi等，2006)和基于注入系数的方法(Garzelli等，2018；Restaino等，2020)。相对于CS方法，MRA方法可以获得更佳的光谱信息，但是其空间细节清晰度相对较差。

VO方法首先建立融合图像与源图像MSI和PAN之间的函数关系(又称先验能量函数)，然后结合不同先验约束构建融合模型，从而将图像融合问题转化为数学优化问题，并通过迭代优化获得最优的融合结果。相对于CS方法和MRA方法，VO方法可以获得更好的高分辨率空间与光谱信息。Ballester等人(2006)首先提出了一种P+XS的VO方法，假设PAN是融合图像多波段线性组合的结果，而MSI由融合图像下采样形成，在此基础上构建融合模型。为进一步提升融合性能，Fang等人(2013)采用了Guided filter描述图像中的相似结构。Möller 等人(2012)使用小波变换基作为函数约束项，提出了一种变分小波多光谱图像融合方法。相对于通过强度构建PAN与融合图像之间的关系而言，利用细节相似性进行描述可以获得更佳的结果，例如，Chen等人(2014)、Li等人(2017)和Tian等人(2020)通过PAN与融合图像间的稀疏梯度关系构建了多种融合模型。Chen等人(2015)采用L2,1范数描述PAN与融合图像间的组梯度稀疏关系，在融合过程中有效考虑了配准问题，形成配准与融合统一模型。相比于全局梯度，局部梯度能更好地描述相似性，因此，Fu等人(2019)在融合模型构建上采用了局部梯度约束。

得益于深度学习方法强大的非线性特征表征能力，DL方法通过深度学习进行多光谱图像融合逐渐成为近年来的研究热点。Huang等人(2015)首先将深度神经网络应用到图像融合领域，通过不同分辨率的全色图像进行训练，生成全色图像的退化模型，并假设多光谱图像的退化过程也遵循这一模型，从而使用训练得到的深度神经网络重建融合图像。Masi等人(2016)和Yuan等人(2018)分别采用卷积神经网络(convolutional neural networks, CNN)和多尺度多深度卷积神经网络提升融合性能。为了保留更多空间信息，Yang等人(2017)提出了一种名为PanNet(deep network architeeture for pansharpening)的融合方法。PanNet利用残差网络获得易丢失的高频信息，再注入融合图像中，从而在保持光谱信息的同时有效提升空间细节信息的清晰度。He 等人(2019)基于CS方法的思想，将细节替换过程映射为深度神经网络，有效减少了光谱失真。Shen等人(2019)使用深度残差CNN构建VO方法中的梯度特征，从而提升VO方法融合模型的准确性。

从以上分析中可以看出，虽然VO方法和DL方法在多光谱图像融合领域中取得了较好的效果，但还有如下难题需要解决：1)如何寻求准确的先验构建有效的融合成像模型对于VO方法是非常重要的，传统方法往往通过线性特征(例如梯度)构建先验建立PAN与融合图像的关系，难以描述自然场景复杂非线性关系，导致成像模型准确性依然有限；模型参数对VO方法影响巨大，传统方法需要手动调参寻求最优模型参数，其调参过程往往过于耗时，且最优模型参数难寻。2)虽然DL方法可以通过非线性关系建立融合图像之间的联系，从而克服VO方法使用线性融合模型的局限性，但是，传统DL方法往往将融合过程当做黑盒，忽略了真实物理成像意义，融合性能依然有待突破。Tian等人(2022)将VO方法中的融合模型求解过程映射为网络架构，提出了一种物理可解译的深度学习多光谱图像融合方法，为解决上述问题提供了一种新的思路，但其利用L1范数构建先验约束导致融合模型准确性依然存在提升空间。

本文提出了一种基于可解译神经网络的多光谱图像融合方法。通过深度学习构建深度先验建立融合图像与PAN之间的联系，由于该先验由学习驱动所得，因此，可以有效提升融合模型先验的准确性；从物理成像机理出发，将MSI看做是下采样的融合图像构建数据保真项，并结合上述深度先验，形成一种新的多光谱图像融合模型，此时，图像融合问题转化为上述融合模型的优化求解问题；通过近端梯度下降法(proximal gradient descent, PGD)对上述优化问题进行求解，进一步将优化求解步骤映射为一种可解译深度网络架构，通过训练数据学习生成最优求解结果。可以看出，该方法的优点主要体现在：1)该网络架构的每个模块对应于求解过程的每个步骤，具有明确的物理可解译性；2)非线性模型先验和融合模型参数由学习所得，有效提升了成像模型的准确性，同时极大降低了传统VO方法最优模型参数选择的难题。

本文的主要贡献为：

1)通过数据驱动形成深度学习映射，从而构建一种新的非线性学习先验，有效提升模型的准确性；

2)基于上述先验构建一种新的融合模型，进一步将融合模型求解过程映射为可解译深度网络架构，避免传统VO方法的调参难题；

3)分别从主观视觉和客观量化分析两个方面，在仿真和真实数据集上对上述方法的优越性进行了有效验证。

2 本文方法

2.1 融合模型建立

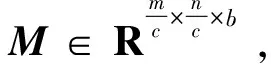
所提出融合模型可以表示为下述优化问题

(1)

式中，J(F)和K(F)分别代表数据保真项和先验约束项。

根据物理成像机制，MS图像M可视为融合图像F经模糊和空间下采样的结果，即M=ΨF+N。Ψ表示模糊和空间下采样运算符，N表示均值为0的高斯噪声。因此，为了在融合图像中有效保持MS图像中固有的光谱特性，常用数据保真项J(F)可以表示为

(2)

为了将PAN图像中的空间细节信息有效传递至融合图像中，传统方法如Chen等人(2015)和Tian 等人(2022)用L1范数构建先验约束描述PAN与融合图像间的残差关系，但由于自然场景特征规律往往较为复杂，难以用仅仅适宜于表征稀疏特性的L1范数去准确描述。为了解决上述问题，拟将其残差关系通过数据驱动由深度学习函数φ进行描述，在此基础上通过深度残差构建先验约束项K(F)，即

(3)

基于上述分析，所提出融合模型可以表示为

(4)

式中，λ为平衡数据保真项和先验约束项的参数。

2.2 模型优化求解

为了求解式(4)，采用PGD方法。引入中间变量Z∈Rm×n×b，此时，式(4)可以转化为如下两个公式进行迭代求解，即

Zt+1=Ft-μΨT(ΨFt-M)

(5)

(6)

通过式(6)发现，Zt+1可以看做F在第t+1次迭代时的重建结果。因此有如下假设：在第t+1次迭代时，F-Zt+1的残差服从均值为0、方程为δ2的独立正态分布(Zhang等，2014)。基于上述假设，可以通过与Zhang和Ghanem(2018)相似的推导，得到如下结论：

定理1：假设x1,…,xk∈Rl是均值为0、方差为δ2的独立同分布变量，X=[x1,…,xk]T。对于任意矩阵A∈Rp×l，可以得到如下结论：

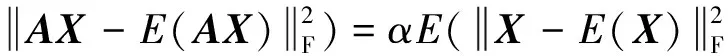
基于定理1，可以得到如下近似

(7)

因此，式(6)可以转化为

(8)

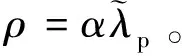
(9)

可以通过Zhang等人(2022)方法从式(9)中求解出Wt+1，进一步地，可以得到Ft+1的近似求解，即

(10)

基于上述分析，所提出模型的优化求解过程可以总结为：

算法1 基于近端梯度下降的模型优化求解算法。

输入：M，P，Ψ，Rp，μ，ρ。

初始化：F0。

循环t=0至最大值：

根据式(5)更新Zt+1。

根据式(9)更新Wt+1。

根据式(10)更新Ft+1。

结束。

输出：F。

2.3 可解译深度网络

将算法1所示的优化迭代步骤展开成多个神经网络模块，从而形成所需的模型可解译融合网络。一方面，利用深度网络的学习能力挖掘全色图像和融合图像之间的结构先验，使得模型更为逼近真实的物理成像关系；另一方面，网络中参数优化不仅受训练数据驱动，同时受物理模型的优化机制所引导，提升训练模型的融合精度；最后，将模型中涉及的超参数设置嵌入在网络模块中，在数据训练中实现超参数自主寻优，避免复杂的手工设计问题。

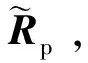
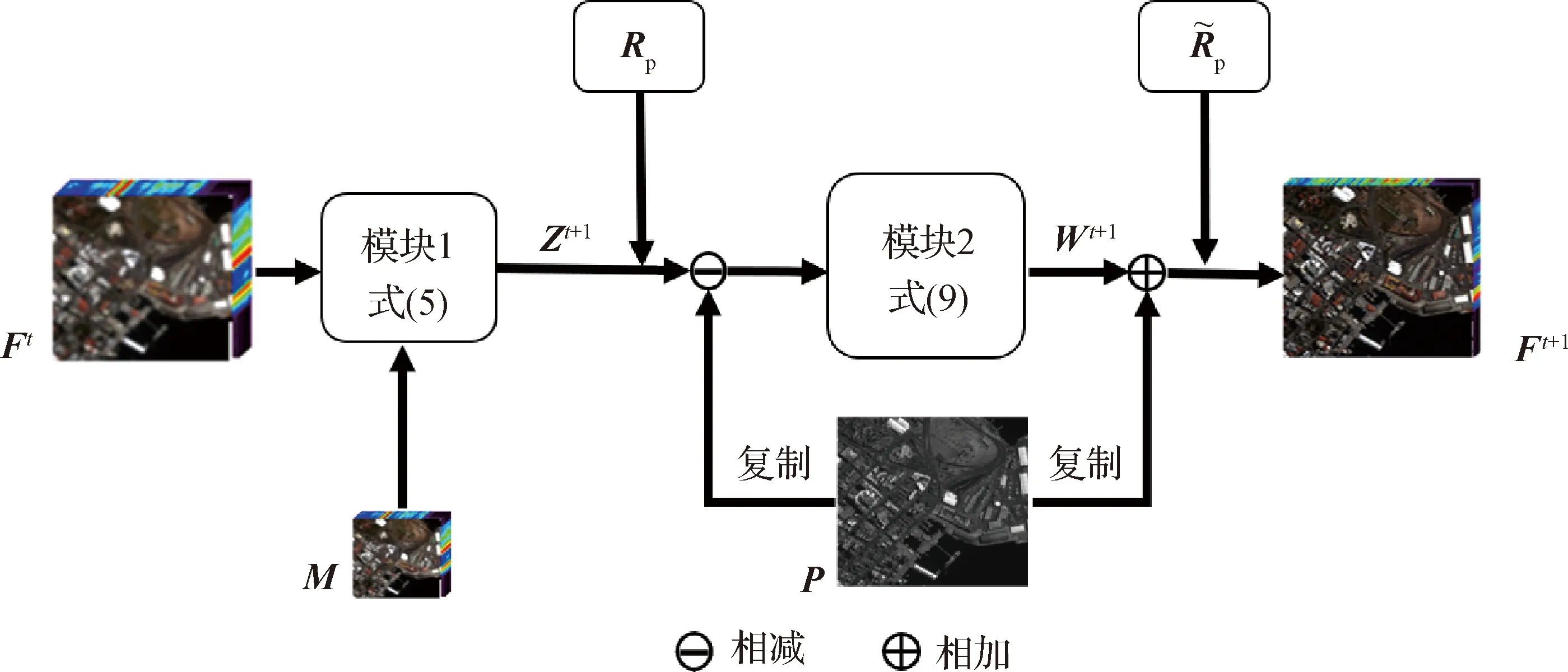
图1 融合网络中第t个网络状态模块

图2 模块2中SwinResUnet的网络结构图

网络模块2的细节网络结构图如图3所示，受Liu 等人(2021)和Zhang等人(2022)方法的启发，本文方法采用结合Transformer和CNN架构的网络模块SwinResUnet(Zhang等，2022)作为式(9)的去噪器。具体来讲，SwinResUnet采用U-Net(Ronneberger等，2015)作为网络主体架构，主要包含3组不同维度下的编码器(E1,E2,E3)和解码器(D1,D2,D3)，中间嵌入特征提取单元F，同时，对应的编码器(Ei)和解码器(Di)之间建立残差短连接结构，增强不同尺度下的特征传递效果。因此，编码器与解码器单元(Ei与Di)特征维度和卷积通道数均一致。E1，E2，E3和F中的1×1卷积单元通道数分别为64，128，256和512。

进一步地，图3(a)展示了所采用的编码器和解码器内部网络细节。如图3(a)所示，编码器(E1,E2,E3)包含黑色虚线之间的网络结构，特征提取单元F包含蓝色虚线之间的网络结构，而解码器(D1,D2,D3)包含红色虚线之间的网络结构。三者结构共享特征提取单元F部分。其中，编码单元在F结构末端加入了大小为2×2(步长为2)的卷积操作实现特征尺寸的下采样；而解码单元在F结构前端加入了大小为2×2(步长为2)的转置卷积操作实现特征尺寸的上采样，以此实现数据的多层语义与结构信息提取融合。对于特征提取单元F，本文方法引入了RConv所表示的残差卷积模块；此外，考虑到全局感受野下不同区域特征的联系，本文方法在RConv单元并行加入了Swin Transformer(SwinT)网络单元。得益于其内部的多头自注意力机制(multi-head self attention, MSA)以及窗口迁移等操作，该结构能够在保证局部光谱和结构特性的情况下，从图像全局层面增强不同区域间空间和光谱信息的交互和融合。在E1,E2,E3和F中，RConv分别采用通道数为32，64，128和256的3×3卷积核对等分后的特征进行处理，SwinT则采用全连接层进行隐式表征，并分别将结果级联后还原为通道数为64，128，256和512的特征。同时，本文方法在每个编码器和解码器的后端和前端分别设计了空间下采样和上采样卷积操作(SConv和TConv)，以此实现不同层级的特征维度变换，获取兼顾高层语义特征和底层细节特征的信息。其中，SConv和TConv分别使用步长和卷积核大小均为2的卷积和转置卷积实现。图3(b)表示的是SwinT和RConv单元网络结构(WMSA(window based multi-head self-attension),SWMSA(shifted WMSA))，可以看到，SwinT网络单元由两个相同的结构单元组成，均包含一个基于窗口的MSA基本单元，以及由两个线性层和介于二者之间的GELU(Gaussian error linear units)非线性层构成的MLP(multilayer perception)基本单元。同时在MSA和MLP前侧使用LN(LayerNorm)层进行标准化并进行残差跳跃连接。图3(b)中RConv则包含两个3×3卷积层以及介于二者之间的ReLU非线性层，同样使用了残差跳跃连接结构。

图3 编码器和解码器内部网络细节

本文采用L1损失函数对网络进行约束并驱动参数优化，即

(11)

3 实验结果与分析

3.1 实验设置

实验主要从仿真实验、真实实验和消融分析3个方面展开。仿真实验主要基于Wald仿真协议：将高分辨率的MSI和PAN分别经过MTF(modulation transfer function)滤波和空间下采样，生成低分辨率的MSI和PAN用于多光谱图像融合实验，将该高分辨率的MSI作为真值图像用于对融合结果进行定性和定量分析。MTF滤波器与理想低通滤波器相似，在Nyquist频率处具有截止幅值。对比真值图像与融合图像的差异，可以首先从主观视觉方面对不同方法的特点进行定性分析。进一步地，可以采用全参考图像质量评价指标对算法的有效性进行定量评估，具体评价指标包括全局相对无量纲误差(relative dimensionless global error in synthesis, ERGAS)、光谱角映射(spectral angle mapping, SAM)、全局综合评分Q2n、结构相似度(structural similarity index, SSIM)、均方根误差(root mean square error, RMSE)、相对平均光谱误差(relative average spectral error, RASE)、通用图像质量指数(universal image quality index, UIQI)和峰值信噪比(peak signal-to-noise ratio, PSNR)。ERGAS和Q2n是多光谱图像融合综合性能评价指标。SAM通过计算融合图像与真值图像对应的两个矢量间绝对角度来测量融合图像的光谱失真情况。SSIM用于衡量图像之间的结构信息相似程度。RASE用于评估融合图像的全局光谱质量。PSNR和RMSE主要从像素差异角度衡量融合结果与真实结果之间的偏差。UIQI用于评价融合图像与参考图像的结构失真程度。

真实实验直接使用原始的MSI和PAN进行融合，用原始数据尺寸进行真实数据的视觉比较和定量分析。由于真实实验中并没有真值图像，本文采用无参考评价指标QNR(quality with no reference)，Ds和Dλ。QNR是一种综合性评价指标，它由空间失真指标Ds和光谱失真指标Dλ所组成(Yang等，2017)，计算为

fQNR=(1-Dλ)α(1-Ds)β

(12)

式中，α和β为系数，默认取值为1。

对比方法包括一种通过23个系数进行多项式内插的插值方法EXP；两种CS方法：GSA(gram-schmidt adaptive)(Aiazzi等，2007)和PRACS(partial replacement-based adaptive component substitution)(Choi等，2011)；两种MRA方法：Indusion(induction scaling)(Khan等，2008)和AWLP(additive wavelet luminance proportional)(Vivone等，2015)；两种VO方法：SIRF(simultaneously registration and fusion)(Chen等，2015)和LGC(local gradient constrants)(Fu等，2019)；4种深度学习方法：PNN(pansharpening by using a convolutional neural network)(Masi等，2016)，PanNet(Yang等，2017)，VPNet(interpretable deep network for variational pansharpening)(Tian等，2022)和本文方法。为了公正比较，实验所有对比方法均运行在配有英特尔至强核心W-2200CPU@3.70 GHz和11 GB显存的GeForce GTX 2080Ti GPU的计算机上。所有对比方法均采用原始默认参数，同时深度学习方法如PNN、PanNet和VP-Net等均使用相同的数据处理方式和数据集。本文采用Adam优化器更新参数，初始学习率的值设置为0.000 5，训练batch大小为16，经过400训练迭代次数达到了稳定的性能。

3.2 仿真实验

本文仿真实验主要采用GeoEye-1和Gaofen-2遥感卫星提供的两组数据集进行多光谱图像融合实验验证。

3.2.1 Gaofen-2遥感卫星数据仿真实验

图4 Gaofen-2仿真数据集融合图像主观视觉比较(选用红、绿、蓝3个波段显示)

根据融合图像与真值图像之间的平均绝对误差生成残差图像，可以验证实验效果。其结果如图5所示。由于存在空间模糊或光谱失真，EXP，GSA，PRACS，Indusion和AWLP(图5(a)—(e))具有较大的残差。通过构建融合模型并进行求解，VO方法可以获得更好的空间与光谱信息的平衡，因此，SIRF和LGC相对于上述方法而言残差较小。通过深度学习，PNN、PanNet、VPNet和本文方法具有较好的融合效果，因此，可以有效地减少残差。相对于其他方法而言，本文方法具有最小的残差，从而表明了本文算法在Gaofen-2遥感卫星仿真数据上具有最好的融合性能。

图5 Gaofen-2仿真数据集融合结果残差图像比较

定量评估方面，通过28幅测试图像进行统计分析，多种评价指标的平均值如表1所示。从表1中可以看出，在GSA，Indusion和AWLP方法中，光谱失真评价指标SAM和RASE表现较差，导致其综合评价指标ERGAS和Q2n与其他方法尚有差距，例如，在上述方法中ERGAS大于5。PRACS，SIRF和LGC可以在光谱失真和空间细节增强方面达到较好的平衡，所以具有较优的综合评价指标(ERGAS在4.0左右)。总体而言，深度学习方法PNN，PanNet，VPNet和本文方法相对于其他方法而言，性能提升显著。例如，对比于LGC，PNN的ERGAS可以有效减少14.45%。本文方法在所有指标上均具有最佳的融合效果，例如，相对于性能第2的VPNet方法，ERGAS可以有效减少7.58%，证明了其在定量评估实验中相对于其他方法的优越性。

表1 基于Gaofen-2仿真数据集28幅测试图像的定量评估结果

3.2.2 GeoEye-1遥感卫星数据仿真实验

图6 GeoEye-1仿真数据集融合图像主观视觉比较(选用红、绿、蓝3个波段显示)

图7 GeoEye-1仿真数据集融合结果残差图像比较

定量评估方面，通过40幅测试图像进行统计分析，多种评价指标的平均值如表2所示。与表1类似，深度学习方法PNN，PanNet，VPNet和本文方法，相对于其他方法而言，各种性能指标提升均较为显著。例如，PNN相对于GSA，ERGAS可以降低19.94%。

表2 基于GeoEye-1仿真数据集40幅测试图像的定量评估结果

总体而言，本文方法在该数据集上优势也较为显著，例如，相对于性能第2的VPNet方法，ERGAS可以有效减少4.61%，因此，在7个客观评价指标上均获得了最佳的效果。

3.3 真实实验

图8 QuickBird真实数据集融合图像主观视觉比较(选用红、绿、蓝3个波段显示)

定量评估方面，本文选取了一组典型测试图像进行统计分析，QNR，Ds和Dλ等无参考评价指标的平均值如表3所示。由于本文方法具有最优的空间清晰度和较优的光谱保真度，所以获得最佳的空间评价指标Ds和较好的光谱评价指标Dλ，从而产生最佳的综合无参考融合性能评价指标QNR，有效证明了本文方法在QuickBird真实数据集上相对于其他方法的优越性。

表3 基于QuickBird真实数据集的定量评估

3.4 消融分析

在本文可解译的融合网络设计过程中，模型迭代次数T(网络状态模块个数)和超参数ρ等初始化设置均对融合性能产生直接的影响，为此，本小节针对以上重要因素对融合网络分别进行了消融实验分析，从而得到最适合的模型架构和网路参数设置，提升多光谱和全色图像的融合质量。

表4给出了不同模型迭代次数下对应的融合网络在GeoEye-1数据集上的测试性能，可以看出，随着T的增加，网络训练也随之增加，且融合指标ERGAS和RMSE在T小于5时下降很快，当T大于5时两项指标下降幅度较小，即随着迭代次数T增加，模型性能提升不再明显，综合训练时间成本和融合性能的权衡考虑，本文将模型迭代次数T设置为5。

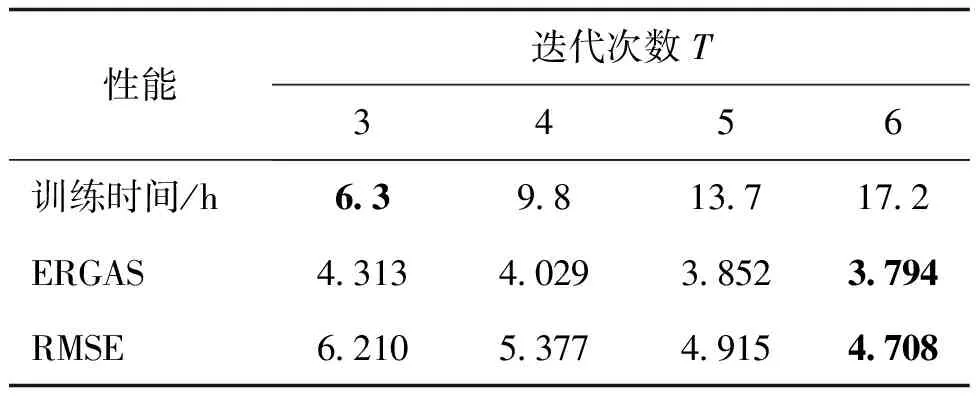
表4 不同迭代次数下的模型性能对比

此外，式(8)中权重参数ρ对于融合结果质量有重要影响，为此，本文设置了多组不同ρ初始化值，并在GeoEye-1数据集进行相同设置下的训练，最后将测试结果统计在表5中。可以发现，当其初始化值设为0.001时综合指标ERGAS取得相对最优的测试结果，光谱保真度指标SAM同样表现最佳。因此，本文方法采用ρ初始值为0.001，从而得到兼顾光谱和空间质量的融合结果。

表5 不同ρ下的融合性能对比

4 结 论

面向多光谱遥感图像融合，本文提出了一种结合VO和DL方法优点的可解译深度网络。首先基于深度先验构建了一种新的多光谱融合模型。接着为了求解融合模型，通过PGD方法将求解过程映射为多个迭代步骤，进一步通过深度展开技术将上述步骤映射为深度网络模块，形成一个具有物理可解译性的深度网络架构。其优势在于：由于深度先验具有更好的非线性表征能力，所以可以有效提升融合模型的准确性。同时，由于模型求解参数由深度网络训练生成，降低了传统VO方法参数设置难度。

为了有效验证本文方法相对于传统方法的有效性，分别在仿真和真实遥感卫星数据集上进行了主客观对比实验。从主观实验中可以看出，本文方法相对于其他方法而言，在保持光谱信息的同时有效增强了融合图像的空间细节信息。客观实验分别使用了全参考评价指标ERGAS，SAM，Q2n，SSIM，RMSE，RASE，UIQI及PNSR和无参考评价指标QNR，Dλ和Ds进行评价。大量统计实验表明了本文方法在上述指标上的优越性。

如何在更多的真实卫星数据上验证本文方法的有效性是未来需要考虑的问题。另外，将本文方法应用于高光谱与多光谱图像融合，也是未来研究方向之一。