面向误差补偿的高光谱与多光谱图像融合

方帅，许漫

1.合肥工业大学计算机与信息学院,合肥 230601；2.工业安全与应急技术安徽省重点实验室，合肥 230601

0 引 言

高光谱图像(hyperspectral image, HSI)提供丰富的光谱信息，广泛应用于图像分类和目标检测等领域。然而，现有成像的光谱分辨率和空间分辨率是相互制约的。因此，HSI通常具有较低的空间分辨率，以保证较高的信噪比，然而如此低的空间分辨率限制了HSI的适用性。与高光谱图像相比，多光谱图像(multispectral image, MSI)通常具有更高的空间分辨率，但是光谱波段较少。将同一场景的低空间分辨率的高光谱图像与高空间分辨率的多光谱图像进行融合，可以重建高空间分辨率的高光谱图像(high-spatial-resolution hyperspectral image, HR-HSI)。

大多现有的方法受光谱字典学习算法启发，先从HSI中学习光谱字典，后对MSI进行稀疏编码来估计系数，从而获得重建的高分辨率高光谱图像。然而仅仅利用光谱字典进行重建目标图像会不可避免地损失一部分空间信息。同时由于遥感图像的地物分布极为复杂，因此其空间信息在不同的区域可能是千差万别的。现有的大多进行误差补偿的算法(Yang等，2020；Yin和Li，2015)也仅考虑了不同通道之间的区别，而忽略了空间信息分布的复杂性，因而存在局限性。

图1展示了Pavia University数据的波段1、波段30、波段50和波段70的水平方向梯度及局部放大图，第1行分别为4个波段的梯度，红色框中区域的放大图对应第2行，蓝色框中区域的放大图对应第3行。从图1中可以看出，不同通道在同一区域表现出了不同的结构特性，同一通道在不同区域也表现出了不同的结构特性。因此，进行误差注入时若只考虑通道之间的不同则很容易忽略每个通道的不同区域之间的差异，从而导致融合结果质量降低。

图1 Pavia University数据梯度及其局部放大图

本文提出了通过一种基于误差补偿的算法来重建高分辨率高光谱图像，即先通过光谱字典学习算法来获得中间结果，再利用残余空间信息对中间结果进行补偿，使得融合结果的质量进一步提高，本文主要贡献总结如下：

1)针对光谱字典学习算法损失空间信息这一问题，提出了误差补偿策略，先利用低分辨率图像构建出空间残差，后在光谱字典学习的基础上进行空间残差信息注入，设计了一种局部区域注入系数算法，使得到的系数能够根据局部区域的光谱特征自适应地调节误差信息的注入，从而避免注入过多或过少的空间信息而导致光谱失真。

2)为保证经过误差补偿后的融合结果在提升空间分辨率的同时不发生光谱畸变，在梯度域探索MSI和HR-HSI之间的关系，构建变分模型。并将该变分模型与1)中构成的优化项结合，从而构建出一个新的模型，该模型中既含有空间方面的约束又含有光谱方面的约束，通过迭代求解逐步提升系数的精度和融合图像的质量。

1 相关工作

尽管各个应用领域对于高分辨率高光谱图像有广泛需求，但由于技术和成本的限制，仍难以同时实现空间高分辨率和光谱高分辨率，因此这个问题引起了广泛关注。学者们利用现有的图像融合技术将同一场景下的HSI和MSI/RGB(red-green-blue)进行融合，从而重建出HR-HSI。

早期高光谱与多光谱图像(HSI-MSI)融合算法从Pansharpening(Alparone等，2007；方帅 等，2020；焦姣和吴玲达，2019)算法借鉴而来，该类算法侧重于细节的提取和注入，由于全色图像不包含任何光谱信息，因此，融合结果通常存在严重光谱畸变。随后出现了一批独立发展起来的HSI-MSI融合算法，主要可分为3类：基于贝叶斯的方法、基于深度学习的方法和基于低维子空间的方法。

基于贝叶斯的方法(Hardie等，2004；Akhtar等，2015)利用观测场景中的先验分布，如高斯先验，并结合最大后验概率实现对问题进行求解。Wei等人(2015)提出一种快速融合的方法，其通过求解与贝叶斯估计相关的Sylvester方程达到融合目的。但是贝叶斯算法依赖于先验假设，而人工设计的先验假设通常是针对某一方面的考虑，并不全面，因而可能导致融合图像质量的降低。

由于深度卷积神经网络(deep convolutional neural networks, DCNN)(Dong等，2014)能够对提取的特征进行分析学习，在HSI-MSI融合领域展现出优越的性能，从而得到广泛应用。Yang等人(2018)提出两分支卷积神经网络(convolutional neural networks,CNN)结构，分别从输入的HSI和MSI中提取光谱特征和空间特征，然后将特征拼接并传递给全连接层，生成HR-HSI。Dian等人(2018b)提出了一种基于深度残差学习的HSI超分辨率方法，该方法使用DCNN学习初始化的HR-HSI和ground truth之间的映射关系。但是基于深度学习的算法通常需要大量的数据用于训练模型，而当前高光谱图像来源较少，这一问题限制了深度学习在高光谱图像融合中的应用。Xie等人(2022)提出了一种MHF-net(MS/HS fusion net)，该方法使用DCNN去噪器估计HR-HSI中间结果的正则化，从而进一步用于求解具有低秩约束的目标HR-HSI。

基于低维子空间的方法假设低分辨率高光谱图像或高分辨率高光谱图像的光谱像素存在于低维子空间，通过提取光谱特征和求取系数来重建HR-HSI，这类方法可分为基于张量分解的方法和基于字典学习的方法。基于张量分解的方法用一个核心张量和3个模方向的字典乘积表示目标高空间分辨率高光谱图像。3D张量可以很好地表示同样具有3维结构的HSI和MSI，基于此，张量分解广泛应用于HSI-MSI融合问题中。Xu等人(2022)提出一种基于张量子空间表示的迭代正则化方法来进行HSI-MSI融合，该方法不仅应用了HR-HSI的全局谱空间低秩与非局部自相似性先验，而且在迭代过程中利用融合结果与输入的低分辨率图像之间的残差信息进行误差补偿。但是该方法在进行迭代补偿残差信息时仅将残差做同等处理，而并未考虑空间信息的补偿，因此方法性能还有很大的提升空间。与矩阵的秩不同，张量的秩是一个非确定性多项式(non-deterministic polynomial, NP)问题,因此基于张量分解的方法通常面临秩的不确定性和分解的不唯一性等问题。

基于字典学习的方法包括空间字典学习和光谱字典学习，对于HSI-MSI融合问题来说，光谱信息比空间信息重要的多，因此光谱字典学习的使用更为广泛。Kawakami等人(2011)首先将稀疏矩阵分解(sparse matrix factorization, SMF)用于HSI-MSI融合，先用稀疏字典学习法估计出光谱字典，后从MSI中估计出系数。Akhtar等人(2014)和Dong等人(2016)设计了一种利用HSI的空间信息非负性来约束解空间的稀疏表示(sparse representation, SR)方法。Han等人(2018)和Fang等人(2018)提出了基于超像素的SR模型，该模型根据空间局部结构自适应调整聚类簇的大小和形状，提高了算法的精度和效率。Dian等人(2019)将非局部相似性与稀疏性先验相结合，同样提高了算法的精度。这几种方法是基于字典学习算法中较为经典的方法，利用先验信息构建正则项来尽可能捕获空间信息，然而这并不足以充分捕获HSI和MSI中的空间信息。为了解决这一问题，Han等人(2020)提出了基于双字典的高光谱图像的融合方法，双字典包括一个常规的光谱字典和一个针对残差图的空间字典，空间字典是为了表征光谱字典重构融合图像而导致空间信息的损失，该方法由于兼顾了光谱信息和空间信息的表示，具有优秀的融合性能。

本文方法与光谱字典学习算法有关，但又与其有很大差异。本文只将字典学习算法所得结果作为中间结果，通过退化模型构造误差对其进行补偿，使得融合结果质量进一步提升。在进行空间残余信息注入时，设计了一种局部区域注入系数，使得到的系数能够根据局部区域的光谱特征自适应地调节误差信息的注入。在残差信息注入的同时还考虑了保持光谱信息不发生畸变，通过优化目标函数，使得到的融合结果在空间和光谱性能上均表现出一定的优越性。

2 问题描述

高光谱图像和多光谱图像融合算法可描述为通过融合同一场景下的HSI和MSI获得HR-HSI。HSI、MSI以及HR-HSI分别用X∈RL×n、Y∈Rl×N和Z∈RL×N表示，其中L和l(L>l)表示图像的波段数，N和n(N>n)表示图像的像素点数目,则X和Y可以表示为Z的线性变换，即

X=ZBM+E1

(1)

Y=FZ+E2

(2)

式中，矩阵B∈RN×N是点扩散函数，M∈RN×n是一个下采样矩阵,F∈Rl×L表示Z映射到Y的光谱响应函数。E1、E2表示残差。

如果用稀疏表示对图像Z进行描述，可表示为

Z=DA+E=T+E

(3)

式中，D∈RL×K表示光谱字典；A∈RK×N是对应的稀疏系数矩阵；K表示字典的原子数，N表示图像像素点数，且K≪N；E∈RL×N表示不能被光谱字典D表达的误差矩阵。

由式(3),结合式(1)和式(2)，有

X=DABM+EH

(4)

Y=FDA+EM

(5)

式中，EH∈RL×n,EM∈Rl×N分别代表HSI和MSI中的误差矩阵，其表示不能被光谱字典表达的空间信息，可以从误差矩阵EH和EM中挖掘出需要的空间残差信息。由于EM中含有更多的空间信息，因此后续主要对EM进行处理。

在进行误差补偿时，首先将初步结果图像T和多光谱图像Y按照相关性进行分组，即计算T的所有波段与Y每个波段的相关系数，得到一个相关系数表。根据表中每列的最大值将T当前波段划分到对应的Y的一组内，对T的所有波段都照此进行，Y有多少个波段就将T分为多少组。将每一组的融合结果Zj(j=1,2,…,l)表示为

Zj=Tj+g.*(Yj-I)

(6)

式中，Tj(j=1,2,…,l)表示第j组图像T；Yj(j=1,2,…,l)表示多光谱图像的第j个波段；g表示误差补偿系数；“.*”表示点乘运算；I表示对于图像T模拟生成的低分辨率亮度分量，这里对图像T进行光谱下采样直接得到I，有

Zj=Tj+g.*(Yj-(FT)j)=

(7)

本文的目标是精确地求解光谱字典D和系数矩阵A以得到图像T，以及在保证不发生光谱畸变的情况下求得误差矩阵补偿系数g进行误差补偿，从而获得精确稳定的融合结果。

3 融合算法

本文主要包括两个模块：初步结果估计模块以及误差补偿模块,如图2所示。初步结果估计模块包括光谱字典训练和基于超像素分割的系数估计。通过输入图像的局部相似性构造正则项，缩小解空间以估计出稀疏系数，从而获取精确稳定的解。误差补偿模块包括误差补偿系数的估计和目标图像Z的重建。设计了一种局部区域注入系数，使得到的补偿系数更能反映对应场景的特征，且为了保证经过误差补偿后的融合结果在提升空间分辨率的同时不发生光谱畸变，在梯度域探索融合图像Z和多光谱图像MSI的关系，构建一个新的目标函数，设计了一种迭代方法，以逐步提高注入系数的精度和目标图像Z的质量。

图2 本文算法框架图

3.1 初步结果估计

3.1.1 字典训练

由于融合图像Z的光谱信息与HSI的光谱信息一致，因此从HSI中学习光谱字典D。由于HSI中具有大量光谱特征相似的地物目标，依据光谱特性采用K-means对HSI进行聚类，再针对每类学习光谱字典，保障字典对各类目标都具有可靠的表达能力，有

i=1,2,…,p

(8)

3.1.2 系数估计

一个典型的自然场景通常包含图像中所有相似像素的集合，而在一个邻域内的像素可能表示相同的地物，因此HR-HSI是局部低秩的。当局部区域变化不丰富时满足局部低秩，为了使用局部低秩先验，首先使用SLIC(simple linear iterative clustering)(Wang等，2017)超像素分割算法对MSI进行分割，在超像素块空间内像素具有同质特性，从而满足低秩假设。同理，HR-HSI也被分成同等数目的超像素，然后在目标函数中添加低秩正则项，构成一个新的目标函数。

局部相似约束可以显著抑制噪声，从而获得更可靠的融合结果。为了利用HR-HSI的局部相似性，假设一个像素可以由与其相似的像素的线性组合来近似，换句话说，该像素的稀疏向量可由同一超像素内所有像素的稀疏向量加权平均得到，即

(9)

构建以下目标函数进行系数求解

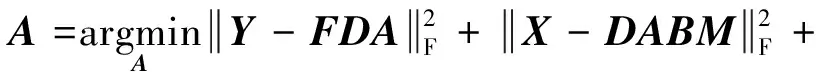
(10)

式(10)是凸函数，因此可以用交替方向乘子法(alternative direction multiplier method, ADMM)(Boyd等，2011)进行有效求解。

3.2 误差补偿

3.2.1 误差补偿系数估计

由问题描述中的分析可知，本文任务之一就是如何将误差EM精确地补偿到初步结果T中。设计一种局部区域误差注入的模型，即利用超像素分割算法将图像分割成多个区域，同一超像素块中的像素具有同质特性，相同的系数增益应用于同一超像素块中的所有像素，从而能够根据局部区域的光谱特性自适应地调整误差信息的注入权重。该模型是一种局部光谱驱动的注入模型，能够尽可能地保持融合后的目标图像的光谱信息不产生畸变。在进行误差补偿时，将初步结果图像T和多光谱图像Y进行分组，每一组对应的补偿系数为

(11)

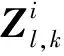
现有的常见方法都只是针对不同的波段计算不同的g，这些方法忽略了图像空间信息的分布是很复杂的，同一波段的不同区域中的结构特性也会相差很大，从图1中即可看出。因此细节恢复并不是只关注通道变化这么简单,同时也证明了本文设计的系数合理性。

3.2.2 目标图像Z估计

现有误差注入算法在进行误差注入时只关注提升空间分辨率，而几乎不会考虑注入过程中光谱信息是否发生畸变，因此融合结果的性能还有很大的提升空间。本文不是仅仅依靠式(7)来获得最终融合结果，而是进一步通过构造一个同时包含空间信息约束和光谱信息约束的目标函数来获得最终的融合结果，使得进行误差补偿后的融合结果在提升空间分辨率的同时不发生光谱畸变。构造以下目标函数来实现，即

(12)

(13)

式中，F为光谱响应函数。

式(12)的3个优化项都是凸函数，因此同样可以使用ADMM对其进行有效求解。

为了提升补偿系数g的精度和融合结果Z的质量，通过迭代更新式(11)和式(12)来实现。即先初始化g为

(14)

式中，T为字典学习算法所得初步结果，然后用初始化的g通过式(12)计算出Z，再用计算出的Z重新计算g，即

(15)

重复上述迭代过程，直至达到设定的迭代次数。通过这样g与Z相互迭代更新，由于融合结果Z的质量越来越高，使得迭代过程中g的估计越来越精确。又正是因为g的估计越来精确，使得补偿的误差越来越精准，从而使得Z的质量越来越高，这是一个相互促进的过程。

4 实验与分析

4.1 实验数据与参数设置

4.1.1 Pavia University数据集

4.1.2 AVIRIS数据集

第2个数据集是由机载可见光/红外成像光谱仪(airborne visible infrared imaging spectrometer, AVIRIS)获取，图像尺寸为300×300像素。数据集的波段1—2，105—115，150—170，223—224等被水蒸气吸收波段后，剩下93个波段，类IKONOS的反射光谱响应滤波器用于生成HR-MSI。使用模板为5×5、标准差为3的高斯滤波器对ground truth进行高斯滤波，然后对每个波段在水平方向和垂直方向上分别进行4倍下采样得到LR-HSI。

4.1.3 真实数据集

4.1.4 参数设置

图3 随参数变化的PSNR曲线

4.2 对比算法和评估标准

为了验证算法的整体有效性，选择6种优秀算法与本文算法进行对比，分别是CNMF(coupled nonnegative matrix factorization)(Yokoya等，2012)、Hysure(Simões等，2015)、NSSR(non-negative structured sparse representation)(Dong等，2016)、LRSR(low-rank and sparse representations)(Dian等，2018a)、OTD(optimized twin dictionaries)(Han等，2020)和IR-TenSR(iterative regularization method based on tensor subspace representation)(Xu等，2022)，其中NSSR、LRSR和OTD是基于字典学习的融合算法。

为了对各算法融合结果进行评价，本文选取4种评价指标检测融合结果的光谱质量和空间质量，分别是峰值信噪比(PSNR)、全局相对误差(relative dimensionless global error in synthesis, ERGAS)、光谱角制图(spectral angle mapper, SAM)和均方根误差(root mean square error, RMSE)。

4.3 实验结果与分析

4.3.1 实验设计

为了验证本文基于误差补偿的高光谱与多光谱图像融合算法的有效性，设计以下实验：

实验1)：为了验证本文误差补偿模块的有效性，在其他优化项以及正则化参数一致的情况下，分别建立初步结果估计模块结果和误差补偿后的结果，对比使用误差补偿前后对融合结果的影响。

实验2)：为了验证本文局部区域误差补偿系数估计的有效性，采用相同方式获得字典学习结果，且在误差补偿模块保证其他优化项相同的基础上，对比局部注入系数与全局注入系数对融合结果的影响。

实验3)：为了验证本文算法有效性，在2个模拟数据集以及1个真实数据集上与其他6个算法进行比较。

实验4)：为了进一步验证本文算法误差补偿部分的普适性，对各对比算法增加误差补偿作为后处理，对比误差补偿算法对于融合效果的影响。

所有算法均在英特尔酷睿i5-8400 CPU和8 GB RAM且装有MATLAB2018a计算机上运行。两个仿真数据集上采用与IKONOS卫星相同的光谱响应函数F(Dian等，2018a)。此外，光谱字典原子数均设置为100。

4.3.2 实验结果与分析

实验1)对比有无误差补偿对融合效果的影响，图4分别为加上误差补偿模块前和加上误差补偿模块后重构的HR-HSI与ground truth之间的误差图及其局部区域放大图。对比可以发现，加上误差补偿后融合结果产生的畸变更小，图像的质量有所提高。从表1中可以看出，进行误差补偿后，融合结果的各项指标均优于无误差补偿的结果，尤其在光谱保持方面有很明显的效果。图5为各算法在AVIRIS数据集上的SAM图，从图5中可以看出,本文算法所得结果的光谱畸变最小，由此说明本文方法的融合结果的光谱特性最佳。

图4 误差图

表1 误差补偿项对比实验结果

实验2)在均使用误差补偿模块的情况下，对比局部注入系数与全局注入系数对融合效果的影响。从表2可以看出，局部注入系数无论是在空间结构方面还是光谱信息保持方面都优于全局注入系数，因此利用局部注入系数所得融合结果的性能更为优越。

表2 注入系数对比实验结果

实验3)在与各算法的对比实验中，图6和图7分别展示了Pavia University数据集第10、16、47波段的伪彩色融合结果和AVIRIS数据集第49、24、11波段的伪彩色融合结果及其对应的MSE图。第1行为融合结果，第2行为对应的MSE图，第3行为MSE图的局部放大图，放大区域为MSE图中红色框部分。从上述图中可以看出，尽管所有算法的融合结果与ground truth相比都存在一些畸变，但是都能恢复大部分空间细节。其中与CNMF、Hysure、NSSR和LRSR这些只利用光谱基或光谱字典的算法比较而言，由于IR-TenSR利用残差信息进行误差补偿，充分利用低分辨率图像的信息，因此误差较小；而本文算法与OTD算法不仅仅使用光谱字典来重建HR-HSI，还利用残差空间信息进行误差补偿，因此本文算法和OTD算法保持空间结构的性能也很优越。

图6 Pavia University数据实验结果及对应MSE图

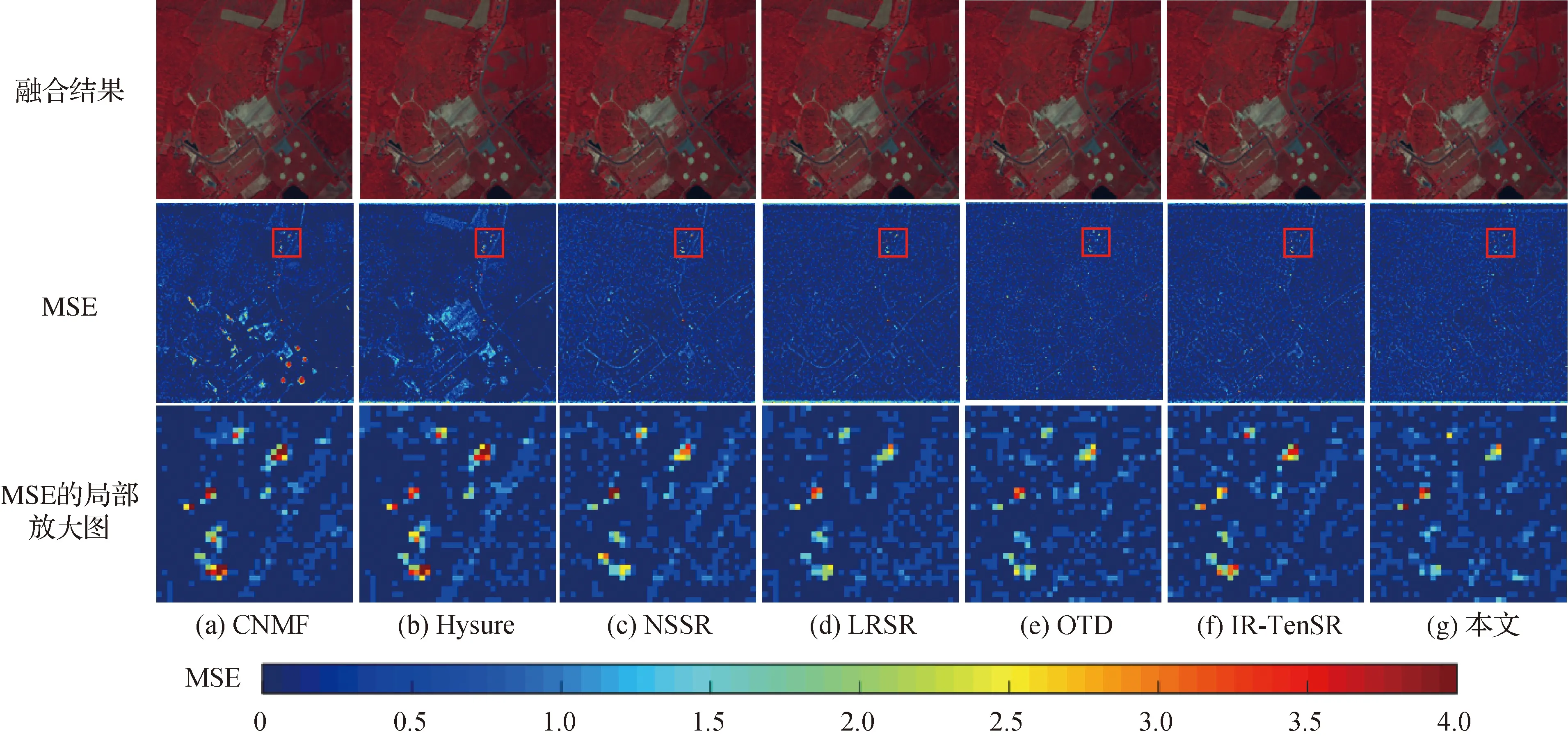
图7 AVIRIS数据实验结果及对应MSE图

图8为各算法在真实数据集上的融合结果，由于真实数据集无参考图像，因此给出其在第16、5、2波段的伪彩色图像，其中图8(a)为LR-HSI第16、5、2波段的伪彩图，图8(b)为HR-MSI第1、2、3波段的伪彩图，由于CNMF融合结果过差，因此未展示CNMF融合结果。从图8中可以看出，除CNMF外，其他算法均能提高LR-HSI的分辨率，但与HR-MSI相比，Hysure和NSSR，LRSR算法不能很好地恢复空间结构, OTD算法融合后的图像存在严重的光谱失真，而IR-TenSR算法光谱失真较小但是空间分辨率较低。相比之下，尽管本文算法重建图像不完美，但是其在光谱失真和空间结构保留之间取得了平衡。

图8 真实数据集实验结果

表3和表4中各指标名称下左栏为各算法融合结果在两个数据集上的质量评价标准下获得的指标值。从客观的指标值中不难看出，由于本文算法在提升空间分辨率的同时将保持光谱信息不发生畸变考虑在内，因此本文算法在空间和光谱性能上均表现出一定的优越性。由于OTD算法在注入空间误差时未考虑空间信息分布的复杂性而直接进行全局注入，导致其融合结果依然存在提升空间。从表3中可以看出，本文算法相对于OTD算法在SAM指标上的精度分别提升了3.5%和8.1%，这对于高光谱图像来说非常重要，因此可以看出本文在光谱信息保持方面有较好效果。

实验4)的结果可参见表3和表4。表3和表4中各指标名称下后处理一栏为各对比算法加上本文算法误差补偿部分后的定量评价指标值。比较表3和表4中两栏指标结果可以看出，在加上误差补偿部分作为后处理后，各算法融合结果的质量都有一定的提升，这也说明了本文误差补偿策略的有效性与价值意义。

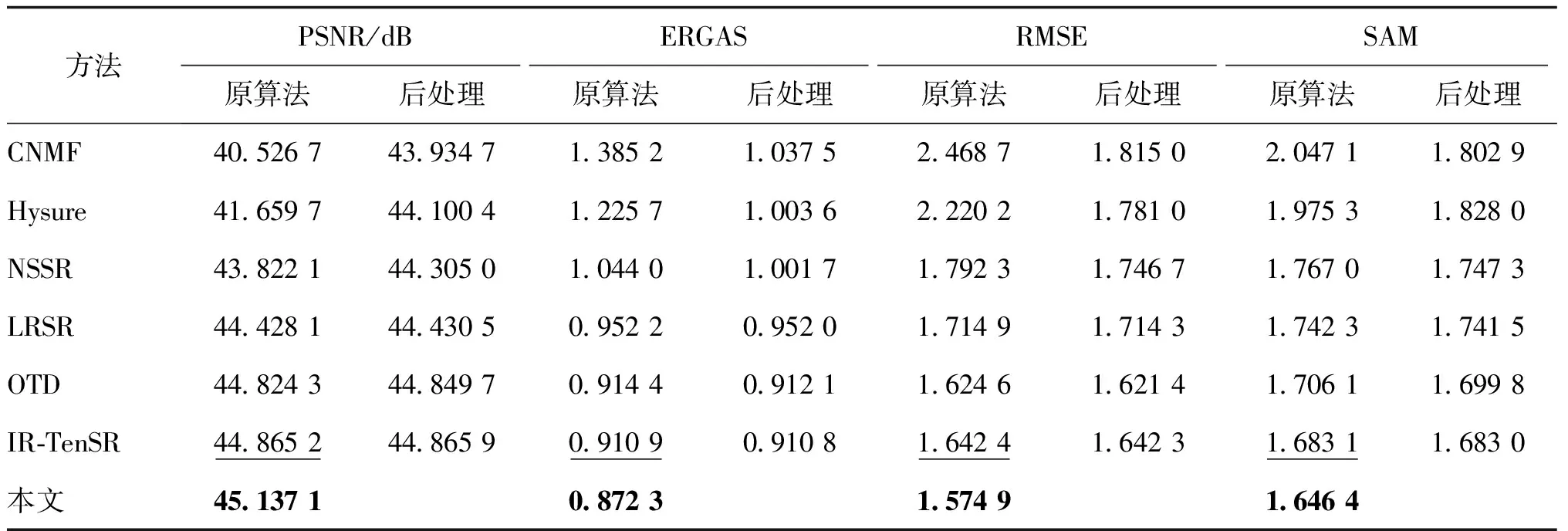
表3 Pavia University数据实验结果

表4 AVIRIS数据实验结果

从表5可以看出，本文算法在时间性能上没有优势，这是因为本文在字典学习算法的基础上添加了误差补偿策略，具有两个目标函数需要进行优化更新，这使得本文的时间复杂度增加、运行时间增长。OTD算法与本文算法类似，均进行空间误差补偿，其算法运行时间与本文相当。

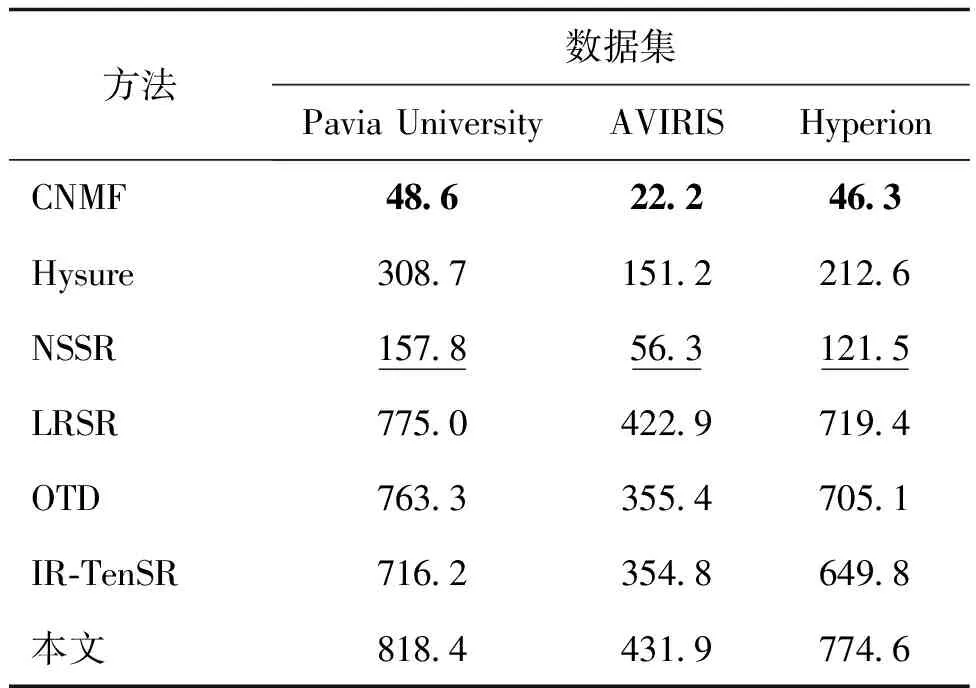
表5 测试算法运行时间

5 结 论

通过对现有高光谱与多光谱图像融合算法的分析，本文提出一种基于误差补偿的融合算法，利用高光谱与多光谱之间的成像关系，计算重建误差在多光谱的各个通道的体现；将多光谱误差以不同比例对高光谱的各通道和各个区域进行精准补偿。在进行误差补偿时，提出基于局部区域的误差补偿系数，使得到的补偿系数更能反映对应场景的特征，因此能够根据局部区域的光谱特性自适应地调整误差信息的注入权重。同时，为了保证经过误差补偿后的融合结果在提高分辨率的同时保持光谱信息不发生畸变，在梯度域提取MSI的空间结构，构造变分模型，并将该变分模型与误差补偿系数优化项结合，进行迭代更新。在Pavia University和AVIRIS两个数据集上，与当前具有代表性的6种优秀融合算法进行比较，本文算法在评价指标以及视觉效果上都取得了有效的提升；在无参考的真实数据集上，本文算法结果在空间和光谱上都呈现出更好的视觉效果。

本文算法主要解决基于光谱字典的融合算法在空间信息误差较大的问题。利用光谱字典得到初步融合结果，而重点是对空间误差的补偿。假设初步融合结果已经充分获得光谱信息，在进行误差补偿时尽量保持光谱信息不发生变化。然而,忽略初步结果在光谱方面同样存在误差的问题，因此，本文算法在光谱信息方面还有很大的提升空间。在未来的研究中，需要提高光谱信息的准确性。此外还可以在不同的域(而不仅仅是梯度领域)中探索HSI和MSI之间的关系。