数字孪生驱动的薄壁件铣削刀具磨损状态识别方法*

宋清华，彭业振，王润琼，刘战强

（1.山东大学，济南 250061；2.山东大学高效洁净机械制造教育部重点实验室，济南 250061）

随着德国“工业4.0”和“中国制造2025”等战略的相继提出，在大数据分析、数字孪生、机器学习等技术推动下，传统制造业正在从基于知识的智能制造向数据驱动和知识赋能的智能制造转型，第四次工业革命即将到来[1–2]。

薄壁零件与传统零件相比具有质量小、强度大的优点[3]。但由于薄壁零件的弱刚性，铣削过程中极易引起薄壁结构的变形、失稳和颤振，造成刀具磨损量急剧增大，从而降低加工精度，甚至影响工件的疲劳寿命，并且加工过程中薄壁零件的时变特性难以在线预测[4–5]。因此研究薄壁件加工过程中刀具磨损状态实时监测，对提高薄壁零件 （如航空发动机零件）的加工精度和加工效率具有十分重要的意义。

传统的刀具磨损状态识别，通常是基于信号分析，不涉及大数据，大多依靠专家经验和现场检查，效率低、准确度低[6]。随着大数据分析技术的崛起，基于机器学习的刀具磨损状态识别方法具有很高的识别准确度，成为近年来机械加工过程中刀具健康管理领域的研究热点[7]。利用多传感器采集加工过程中的切削信号、数字图像等，结合大数据流式处理、自然语言处理等机器学习算法，确定信号特征集与刀具磨损之间的映射关系，从而建立数据驱动模型，识别刀具加工过程中的磨损状态，并将其反馈给数控加工平台，准确选择换刀时机。此方法不仅可以提高刀具本身的利用率，而且极大地提高了薄壁件的加工效率和表面质量[8–9]。Li 等[10]通过对振动信号的频谱分析，得到一组监测指标，并通过模糊神经网络描述了刀具磨损条件与这些指标之间的关系，得出了可行性结果。Li 等[11]通过相关性分析选择了14 个时域特征，建立了v–支持向量回归 （v–SVR）预测模型来监测刀具磨损，试验结果表明，v–SVR 模型的预测准确率高达96.76%。廖小平等[12]提出了一种利用核主成分分析法实现特征降维，基于灰狼优化算法优化SVM 的刀具磨损状态识别模型，该模型具有较好的泛化能力。

基于机器学习的刀具磨损状态监测提高了识别精度，但多数研究高度依赖仿真数据和离线数据来优化刀具路径和加工过程，缺少在加工过程中利用在线数据做出实时有效的决策。同时，机床加工过程与虚拟数据之间缺乏交互，从而使得数据驱动的刀具磨损状态识别模型具有一定的滞后性，造成识别结果的片面性。

在目前制造模式向数字化、网络化和智能化发展的大背景下，机床加工过程实时监测以及刀具状态诊断管理的智能性、主动性和预测性是亟待解决的问题。数字孪生 （Digital twin，DT）技术是以多维模型和融合数据为驱动，通过实时连接、映射等方式在数字空间对物理世界的物体模型进行描述、诊断、预测和决策[13–14]。

近年来，数字孪生的出现为连接物理世界和虚拟世界提供了有效的技术手段[15]。Atluru 等[16]开发了智能机床状态监测系统，通过优化加工前、加工中和加工后的加工参数，最大限度地缩短了加工时间，提高了产品质量。Zhuang 等[17]提出了一种基于数字孪生驱动的车削过程刀具磨损监测与预测方法，该方法建立了与实际刀具系统完全匹配的对称虚拟刀具系统，实现了刀具磨损的高精度监测和预测。Christiand 等[18]提出了一种利用电流数据监测微型刀具磨损情况的数字化孪生方法。尽管数字孪生技术的应用越来越广泛，但应用于薄壁件铣削加工过程监测的研究工作相对较少。

基于数字孪生技术，利用实时数据驱动刀具磨损状态识别模型，可全方位、多角度预测薄壁件铣削过程中刀具磨损状态。因此，本文提出一种数字孪生与GSCV–SVM 算法融合驱动的薄壁件铣削加工过程中刀具磨损状态识别方法，基于数字孪生的理念，利用其虚实融合、实时交互的优点，构建机床加工过程中的数字孪生体，融合GSCV–SVM 算法，借助MySQL 数据库，实现了薄壁件铣削过程信号实时监测以及刀具磨损状态的在线识别。该方法可保障薄壁件铣削加工过程稳定、高效地进行，对促进加工质量和加工效益的提升具有重要意义。

1 刀具磨损状态识别模型建立

1.1 数字孪生驱动的识别框架

如图1所示，物理空间与虚拟空间通过数字孪生技术实现了信息传输与决策反馈。根据物理空间中数控铣床的几何参数，搭建数控铣削加工平台模型。在保证高保真的前提下，利用拓扑轻量化方法，使用最少的点线面重构原模型，实现模型的减面。然后将三维模型的面铺平展开成一个对应的二维 （U、V）坐标图像，进行纹理贴图，进一步优化模型，为数字孪生体的构建提供模型保障。通过传感器采集铣削加工过程中的切削信号 （加速度、力和声音等），经特征提取与滚动时间窗口切片实现降采样处理后传输至数据库。在虚拟空间中，结合机器学习算法与高保真模型构建机床加工过程数字孪生体。利用HTML、CSS 和JavaScript搭建可视化平台，并将孪生体嵌入进去，实现薄壁零件铣削过程的信号实时监测和刀具磨损状态的在线识别。根据刀具磨损所处的状态，将换刀指令反馈给数控机床，从而实现实时数据的交互。

图1 数字孪生驱动的刀具磨损状态识别框架Fig.1 Tool wear state recognition framework driven by digital twin

1.2 基于SVM 的刀具磨损状态识别

对铣削过程中的切削信号经过特征提取和选择后，就可对数据集进行分类，即识别刀具磨损状态，将刀具磨损分为3 类：初期磨损、正常磨损和剧烈磨损。因此，可以借助多类SVM实现对多种磨损状态的识别[19]。给定一组带标签的训练样本{（xk，yk）}l k，其中，xk为第k个训练样本 （xk∈Rn）；yk为训练样本对应的分类标签 （假设yk∈{E0，E1}，E0为初期磨损状态；E1为正常磨损状态），如图2所示，假设属于E0的特征均满足方程w·xk+b>0；属于E1的特征均满足w·xk+b<0。其中，w为n维权重向量；b为偏置值。SVM 的目标是寻找一个最优的决策面，在保证正确分开两种磨损状态的同时，分类间距最大[20]，该最优决策平面可表示为

假设最优决策平面分别上下移动c，经等式变换，得到对应间隔上下边界的方程w·xk+b=1 和w·xk+b=–1，称为正负决策平面。训练样本中距离最优决策平面最近的数据点称为支持向量，由图2可知分类间隔为2/||w||，由此根据最大分类间隔，确定SVM 优化模型为

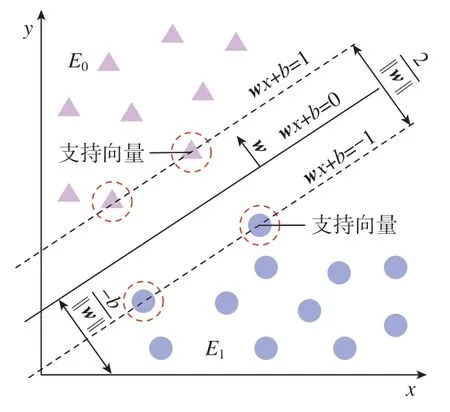
图2 支持向量机分类原理Fig.2 Classification principle of support vector machine

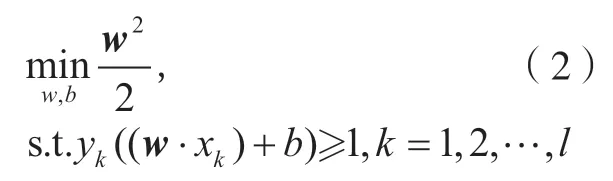
如图3所示，如果训练样本中出现了异常状态点，特别是异常状态点出现在了另外一类状态分类标签中，此时若仍不放松对最大间隔的要求，则无法将两类样本线性分开，为此引入松弛变量ζk，从而在偏离最大间隔一定范围内允许异常状态点存在，此时约束转变为

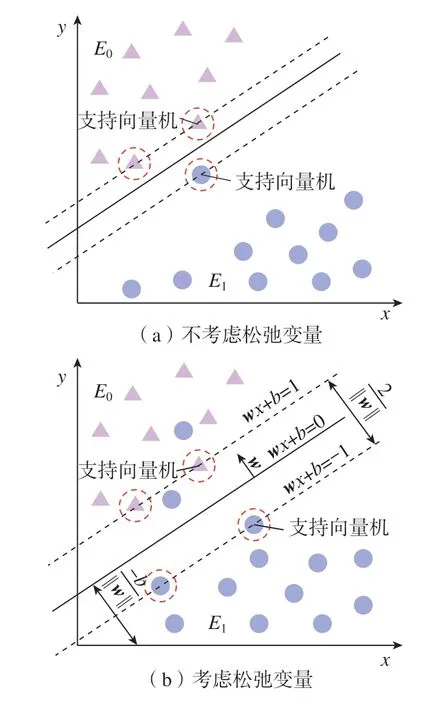
图3 松弛变量的影响Fig.3 Effects of relaxation variables

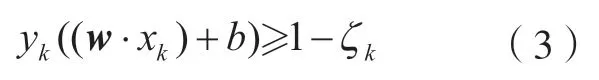
在目标函数中考虑异常状态点的离群带来的损失，就需要加入一个惩罚因子C，二者呈正相关，此时SVM 优化模型变为

式中，松弛变量ζk>0；惩罚因子C>0。

式（4）为一个凸约束问题，可以通过拉格朗日乘子法，将原问题转化为对偶问题进行求解。

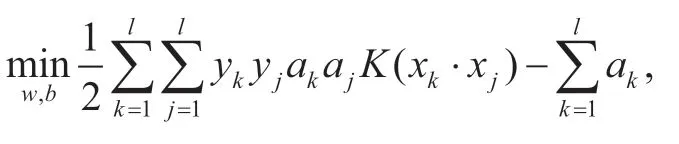
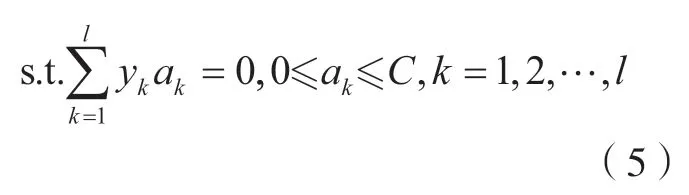
式中，K（xk·xj）为核函数，所提出的刀具磨损状态识别方法中的核函数为径向基函数，即K(xk∙xj)=

由于识别对象是3 种磨损状态，因此采用多分类的方法，即1 对1 法（One vs one，OvO）。本文构造了3 个二元分类器，每个分类器都由两个对应磨损状态的数据训练。当对一个未知状态的训练数据进行分类时，最后得票数最多的是样本的预测标签。

2 试验验证

2.1 数据采集与处理

本文采用的铣削试验数据来源于2010年PHM 公开数据集，试验装置及过程如图4所示。铣削加工参数如表1所示。

表1 铣削工艺参数Table 1 Milling process parameters

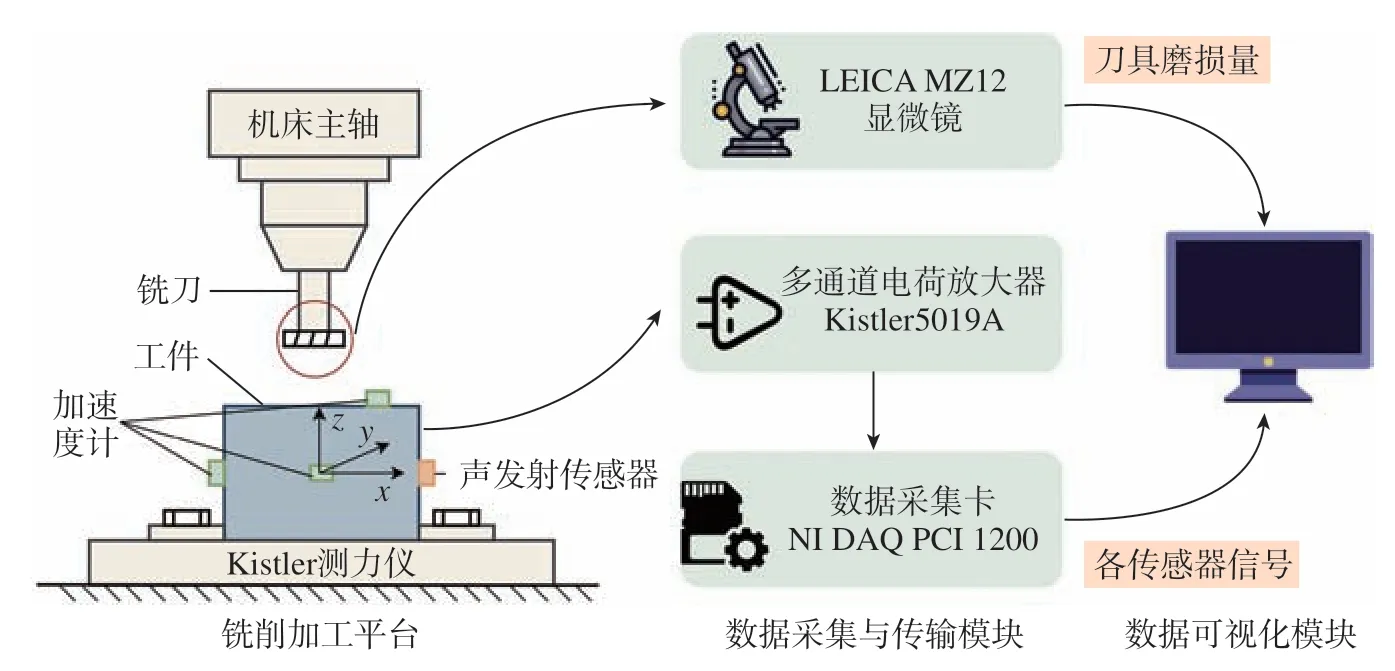
图4 试验系统和主要设备Fig.4 Experimental system and main equipment

每次走刀的铣削工艺参数相同，且工件形状、尺寸一致，因此每次走刀时间间隔相等。通过NI 数据采集卡采集铣削过程中的加速度、声音以及切削力信号，同时利用显微镜测量并记录每次走刀后铣刀的后刀面磨损量。该数据集收集了6 把独立铣刀 （编号为C1～ C6）全生命周期的加工数据，每次试验记录315 次走刀。本文通过分析C4 铣刀试验数据集中x方向加速度信号，构建了基于GSCV–SVM 算法的刀具磨损状态识别模型，并对C6 铣刀的磨损状态进行了预测辨识。图5所示为C4 铣刀3 个切削刃的平均磨损量变化曲线，结合铣削加工过程的实际情况，确定前20次走刀为初期磨损阶段；21～215次走刀为正常磨损阶段；215 次走刀后进入剧烈磨损阶段。

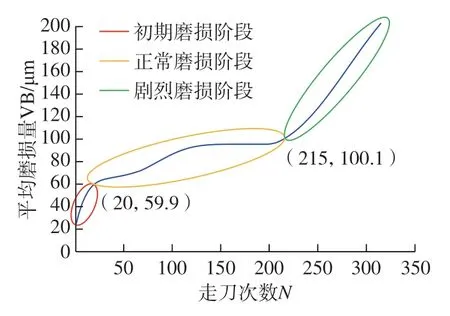
图5 C4 铣刀平均磨损量变化曲线Fig.5 Variation curve of average wear of C4 milling cutter

本文通过时、频域分析，提取铣削振动信号的标准差、均方根和均方频率，作为反映刀具磨损的时域和频域特征，如表2所示。3 个特征值随磨损量变化的规律如图6所示。

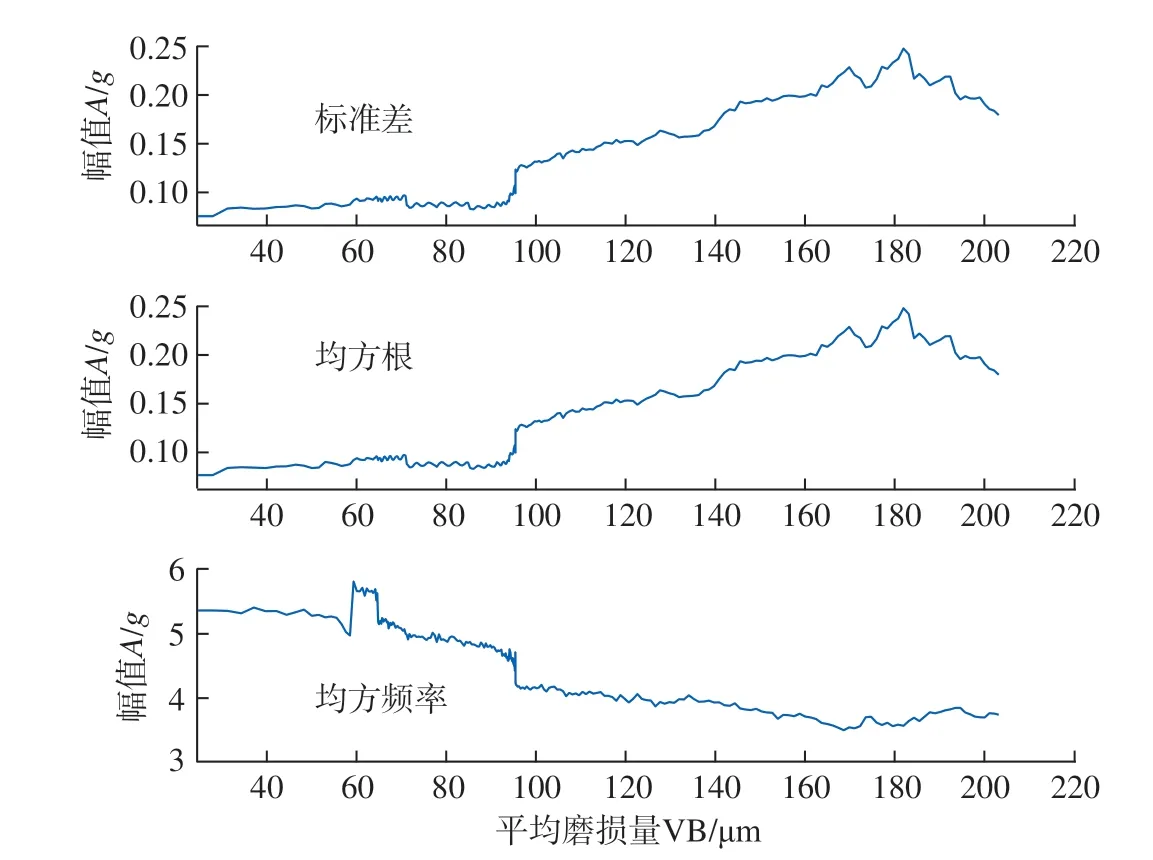
图6 时域、频域特征参数变化图Fig.6 Variation diagram of characteristic parameters in time domain and frequency domain

表2 时域、频域信号的特征值及表达式Table 2 Features and expressions of time domain and frequency domain signals

小波包分解是在小波分析的基础上，根据信号特征和分析要求，对信号的高频和低频空间均进行了分解，从而在更大范围内找出与信号频谱相匹配的合适频段[21]。使用小波包分析法分析此加速度信号时，频带分辨率应小于518 Hz，试验中信号的采样频率为50 kHz，利用db3 小波滤波器进行分解，由式（11）求得小波包的分解层数为6。

式中，Fs为信号采样频率；n为小波包分解层数；fmin为最小频段。

通过铣削振动信号的频谱分析，可知振动频率大多分布在10 kHz 以内，因此取64 个频带中的前32 个频带 （1～12.51 kHz）能量作为时频域特征。图7为部分频带能量和小波包能量熵随刀具磨损量变化情况，均较好地反映了刀具磨损状态的变化。利用相关系数法，计算32 个频带能量和小波包能量熵以及时域、频域中的特征向量与磨损量之间的相关系数|ρxy|，最终确定出14 个|ρxy| >0.9 的特征向量，部分特征向量与磨损量的相关性如表3所示，组成特征向量集T=[p1，p2，p3，…，p4]作为GSCV–SVM 模型的输入向量。

表3 特征向量与磨损量的相关系数Table 3 Correlation coefficient between eigenvector and wear

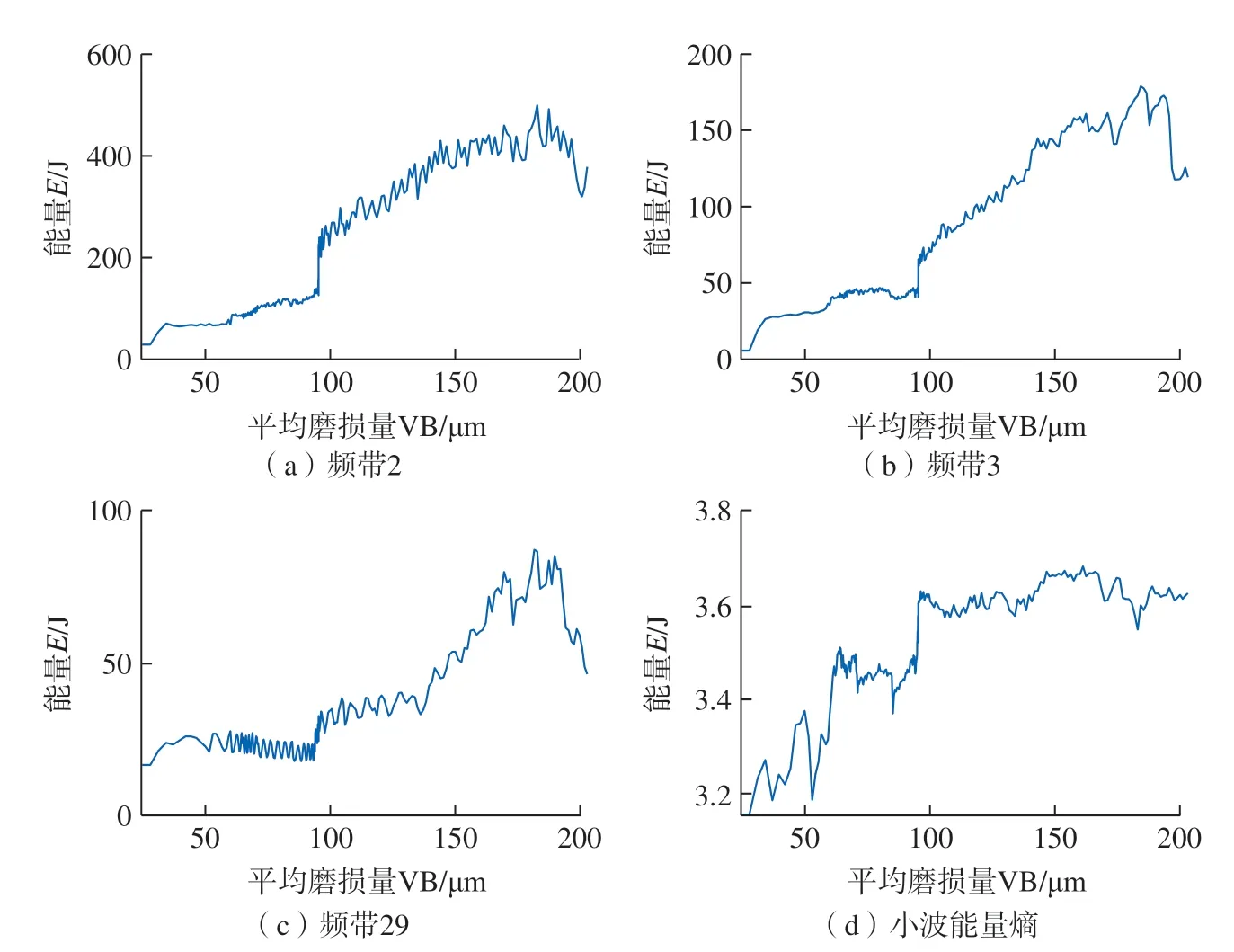
图7 时频域特征参数变化图Fig.7 Variation diagram of characteristic parameters in time-frequency domain

2.2 刀具磨损状态识别

根据上文对C4 铣刀磨损状态的划分情况，从3 种状态中分别随机抽取10 组、150 组、80 组特征向量构成训练集，共计240 组；剩余75 组数据构成测试集，基于GSCV–SVM 的刀具磨损状态识别算法流程图如图8所示。

图8 刀具磨损状态识别算法流程图Fig.8 Flow chart of tool wear state recognition algorithm

分别对训练集和测试集进行归一化处理，利用网格搜索法查找范围内所有的点进行参数寻优，得到尽可能多的超参数组合，再通过交叉验证（K-fold cross-validation，K-CV）重复3 次，找出使得测试集分类准确度最高的C、g超参数组合。寻优结果如图9所示，最终确定惩罚因子C=4、核参数g=2。利用得到的最优参数，结合SVM 算法训练刀具磨损状态识别模型，用测试集检验分类器的性能，识别结果如图10（a）所示，识别准确率为96%（72/75）。

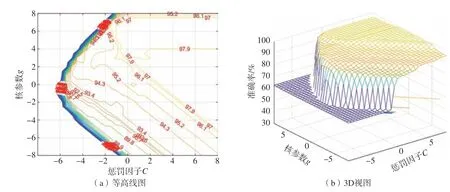
图9 超参数C、g 寻优结果Fig.9 Optimization results of super parameters C and g

利用C6 铣刀数据集进一步检验模型的泛化能力，通过对数据集进行特征提取和特征选择，确定特征向量集，并进行归一化处理后，作为测试集验证基于GSCV–SVM 的刀具磨损状态识别模型的泛化能力，识别结果如图10（b）所示，识别率为90.16%（284/315）。

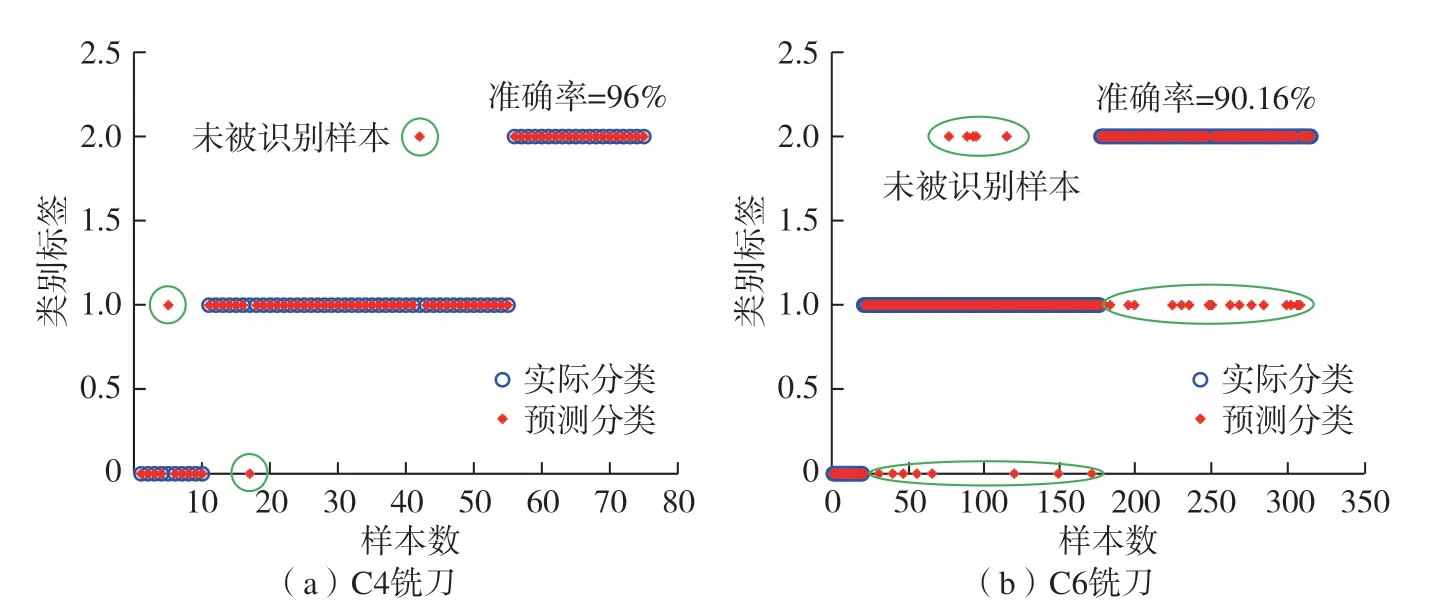
图10 两种铣刀磨损状态识别结果Fig.10 Identification results of two types of milling cutter wear state

综上识别结果分析，薄壁零件铣削刀具磨损状态模型中仅有两个参数需要寻优，且样本数量较少。而支持向量机 （SVM）具有使用非线性核/泛化能力强和训练样本量小等特点。此外，所提方法考虑松弛变量的影响，使得模型具有较好的鲁棒性。同时利用循环遍历的网格搜索，根据模型精度确定最佳超参数，交叉验证过程中防止训练过拟合，从而使得模型具有较高的识别精度和泛化能力。

3 结论

为了实现薄壁零件铣削过程的刀具磨损状态在线识别，提出了一种数字孪生与GSCV–SVM 算法融合驱动的刀具磨损状态识别方法，通过试验验证了方法的有效性，针对薄壁零件铣削中的刀具磨损，该方法具有较高的识别精度和泛化能力。本文的主要内容总结如下。

（1）所提出的方法通过网格搜索与交叉验证 （GSCV）的寻优方式，最终确定了超参数组合惩罚因子C=4、核参数g=2 是全局最优解，避免了局部最优。在此超参数组合下，模型的识别精度与泛化能力较好。

（2）通过对薄壁零件铣削过程中加速度信号的时域、频域以及时频域特征提取，建立信号特征与刀具磨损的实时映射关系，从而准确识别了刀具磨损状态。试验结果表明，不同铣刀磨损状态的识别准确率分别为96%和90.16%，具有识别准确率高，且模型具有较好的泛化能力，进一步验证了SVM 在小样本分类识别问题的优越性。

（3）利用数字孪生技术，经模型轻量化处理后，结合GSCV–SVM 算法构建高保真的数字孪生体，将物理空间中机床加工过程映射到虚拟空间，实现了薄壁零件铣削过程的信号实时监测以及刀具磨损状态的在线识别。

除此之外，在今后的研究中也应考虑到该方法的几个局限性。首先，所提出的试验验证方法需要改进，设计不同铣削参数的薄壁零件铣削试验，进一步验证模型在不同工况条件下的泛化能力。其次，该方法在大样本的条件下有一定的局限性，可以考虑结合随机梯度下降法 （Pegasos）优化SVM 算法。