新陈代谢灰色模型在新冠肺炎确诊病例数预测中的应用
陈勤

摘 要:为提高新冠肺炎确诊病例数预测精度,将新陈代谢灰色模型应用于2020年1月30日至2月10日宜昌市新冠肺炎确诊病例数进行模拟与预测。结果表明,确诊病例数新陈代谢灰色模型是精度等级较高的一种预测模型,为新冠肺炎确诊病例数的预测提供了简单可靠的路径,为未来疫情防控工作提供一定的参考。
关键词:新陈代谢;灰色模型;确诊病例数;新冠肺炎
中图分类号:TB 文献标识码:A doi:10.19311/j.cnki.16723198.2023.02.084
近两年来,新冠肺炎疫情在全球多个国家不断蔓延,根据世界卫生组织在2022年7月15日公布的最新数据显示,全球累计新冠肺炎确诊病例557917904例,累计死亡病例6358899例,疫情仍在持续,且奥密克戎亚型变异株BA.4、BA.5的传播力和隐匿性更强。在这场全球公共卫生安全危机下,如何精准快速地预测疫情的发展趋势,为各级政府及医护人员提供有效的数据信息,协助其提前制定应对措施且采取积极有效的方案,可在一定程度上阻止疫情的进一步传播和加重。在疫情预测系统中,确诊病例数的预测是衡量疫情发展状况及其严重程度的重要指标之一,对确诊病例数进行准确合理的预测具有重要意义。有学者采用如ARIMA模型、指数平滑模型等对新冠肺炎疫情确诊病例数进行了预测,获得较好的预测效果。新陈代谢灰色模型通过去掉老信息且及时补充新信息的方式使得数据稳定性更高、随机性降低,在预测精准性上具有一定的优越性,因此本文采用2020年1月30日至2月10日宜昌市新冠肺炎确诊病例数据建立新陈代谢灰色模型进行模拟和预测,为未来疫情防控工作提供参考。
1 数据来源
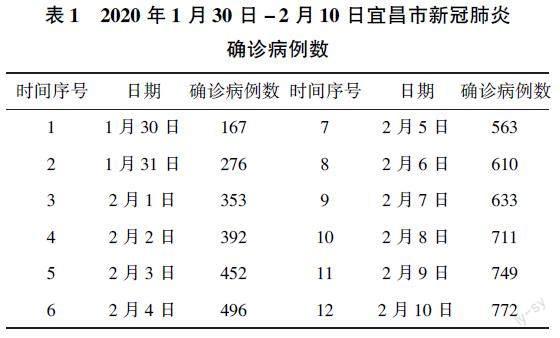
本文以宜昌市2020年1月30日至2月10日新冠肺炎确诊病例数为研究对象,使用的全部数据来源于湖北省卫生健康委员会网站(http://wjw.hubei.gov.cn/)公布的每日疫情通报,具体数据见表1。
2 新冠肺炎确诊病例数新陈代谢灰色模型构建
2.1 确诊病例数灰色GM(1,1)模型的建立
設原始确诊病例数序列为X(0)=(x(0)(1),x(0)(1),…,x(0)(t)),其中:x(0)(t)代表第t天确诊的病例数。对X(0)累加生成确诊病例数1-AGO序列为X(1)=(x(1)(1),x(1)(2),…,x(1)(t)),其中:x(1)(k)=∑ki=1x(0)(i),k=1,2,…,t。在确诊病例数1-AGO生成序列基础上,形成确诊病例数紧邻均值生成序列为Z(1)=(z(1)(2),z(1)(3),…,z(1)(t)),其中:z(1)(k)=(x(1)(k)+x(1)(k-1))/2,k=2,3,…,t。
建立确诊病例数灰色GM(1,1)预测模型的白化方程为dx(1)dt+ax(1)=b,其中:
a∧=(a,b)T=(BTB)-1BTY
Y=x(0)(2)x(0)(3)x(0)(t),B=-z(1)(2)1-z(1)(3)1-z(1)(t)1
得到该预测模型白化方程的时间响应方程为x(1)∧(t+1)=(x(1)(1)-ba)e-at+ba,原始数据还原值为x(0)∧(t+1)=x(1)∧(t+1)-x(1)∧(t)。
对于确诊病例数灰色模型的有效性验证,本文以均方差比值检验方法为主,参考相对误差检验结果。当均方差比值C<0.35时精度等级为一级,C<0.5时为二级,C<0.65时为三级,C0.65时为四级。相对误差结果则以0.01,0.05,0.10,0.20为临界值依次划分为一至四级精度等级。
2.2 确诊病例数新陈代谢灰色模型的建立
去掉确诊病例数原始数据序列X(0)的一个老信息x(0)(1),同时补充一个新信息x(0)(t+1),形成新的确诊病例数序列为X(0)=(x(0)(2),x(0)(3),…,x(0)(t+1))。以此作为原始数据序列建立确诊病例数新陈代谢灰色模型为x(0)(k)+az(1)(k)=b,k=1,2,…,t,其中:a∧=(a,b)T,Y=x(0)(3)x(0)(4)x(0)(t+1),B=-z(1)(3)1-z(1)(4)1-z(1)(t+1)1
按2.1节进行运算,即完成了一次新陈代谢,获得新的确诊病例数预测结果。重复以上流程,去掉原始确诊病例数序列X(0)中的一个老信息x(0)(2),同时补充一个新信息x(0)(t+2),形成新的确诊病例数序列为X(0)=(x(0)(3),x(0)(4),…,x(0)(t+2)),以此作为确诊病例数原始数据序列进行运算,不断剔除老旧信息,增加新的数据,即建立了确诊病例数新陈代谢灰色模型。
3 确诊病例数新陈代谢灰色模型计算与分析
3.1 确诊病例数原始数据的处理
由表1选择时间序号1-5号,即2020年1月30日至2月3日宜昌市新冠肺炎确诊病例的数据X(0)=(167,276,353,392,452)进行建模,累加生成得到确诊病例数1—AGO序列X(1)=(167,443,796,1188,1640)和确诊病例数紧邻均值生成序列Z(1)=(305,619.5,992,1414)。由2.1节可设B和Y,代入a∧=(a,b)T=(BTB)-1BTY中,可得a∧=(-0.15,241.76)T,将参数a,b的值代入2.1节中白化方程的时间响应方程,化简可得确诊病例数X(1)的时间响应方程为:
x(1)(t+1)=1757.53e0.15t-1590.53∧x(0)∧(t+1)=x(1)∧(t+1)-x(1)∧(t),
分别将t=1,2,3,4代入上述方程组,得到确诊病例数的模拟值序列X(0)∧=(289,336,391,455)。
利用确诊病例数灰色模型求出确诊病例数原始序列X(0)的模拟数据序列X(0)∧,建立残差序列ε(0)=(ε(0)(1),ε(0)(2),…,ε(0)(t)),其中ε(0)(k)=x(0)(k)-x(0)∧(k),k=1,2,…,t,将上述数值代入得到残差序列ε(0)=(-13,17,1,-3)。依次计算确诊病例数残差序列均值ε-=0.5,确诊病例数残差序列方差s21=116.75,确诊病例数原始数据序列均值x-=328及原始数据序列方差s22=9744.4,由C=s1/s2计算均方差比值为0.1095<0.35,精度等级为一级。同时求出该预测模型的平均相对误差结果为Δ-=0.0259,精度等级接近一级。综合来看,该预测模型具有较高的合理性与有效性,预测结果可信度较强。
3.2 确诊病例数的模拟和预测
对确诊病例数原始数据序列X(0)=(167,276,353,392,452)做等维处理,去掉一个老信息167(1月30日确诊病例数),增加一个新信息496(2月4日确诊病例数),形成一组新的原始数据序列X(0)=(276,353,392,452,496),根据确诊病例数新陈代谢灰色模型实施8次运算,并对所得8组模拟值做均方差比值检验,结果见表2。
分析表2结果发现,预测模型经过8次运算,第2组模拟值的均方差比值最小,第8组模拟值的均方差比值最大,且最大均方差比值小于0.35,由表2可知其精度等级均为一级,本文建立的确诊病例数新陈代谢灰色模型通过了均方差比值检验。计算得到第1-8组预测结果的平均相对误差分别为0.0259,0.0083,0.0087,0.0077,0.0224,0.0143,0.0145,0.0215,其中有3组平均相对误差小于0.01,达到一级精度等级,另外5组接近一级精度等级。综合均方差比值检验和平均相对误差结果,都表明该模型具备较好的预测优势,有效且可实施。
最后,采用新陈代谢灰色模型对2020年2月3日-10日,即时间序号为第5-12天的宜昌市新冠肺炎确诊病例数进行预测,得到确诊病例数的预测值序列为(455,499,562,613,645,701,752,785),计算得残差序列ε=(-3,-3,1,-3,-12,10,-3,-13),相对误差序列Δ=(0.0066,0.0040,0.0018,0.0049,0.0190,0.0141,0.0040,0.0168),平均相对误差
Δ-=0.00915<0.01,这表明确诊病例数新陈代谢灰色模型的平均相对误差检验达到一级精度,其平均预测精度高达约99.085%。
4 结论
新冠肺炎确诊病例数受到众多不确定性因素的影响,数据具有一定的波动性、模糊性和随机性,是比较明显的灰数,需要在建模过程中不断地剔除过时的数据,补充新的数据,以保证信息的“与时俱进”。因此本文提出应用新陈代谢灰色模型对新冠肺炎确诊病例数进行模拟和预测,并采用2020年1月30日-2月10日宜昌市新冠肺炎確诊病例数据对新陈代谢灰色模型的有效性进行了验证,结果表明确诊病例数新陈代谢灰色模型是精度等级较高的一种预测模型,为新冠肺炎确诊病例数的预测提供了一种简单可靠的路径,对后期疫情防控具有一定的参考价值。
参考文献
[1]李星,赵露露,金新政.武汉市新型冠状病毒性肺炎患者数动态趋势预测——基于灰色预测模型[J].卫生软科学,2020,34(11):8588.
[2]白璐,郭佩汶,范晋蓉.湖北省新冠肺炎确诊人数的建模与预测分析[J].检验检疫学刊,2020,30(2):1012.
[3]王旭艳,喻勇,胡樱,等.基于指数平滑模型的湖北省新冠肺炎疫情预测分析[J].公共卫生与预防医学,2020,31(1):14.
[4]曾波,刘思峰,方志耕,等.灰色组合预测模型及应用[J].中国管理科学,2009,17(5):150155.
[5]李丽丽.基于灰色建模技术的大规模地震应急救援物资需求预测研究[D].重庆:重庆工商大学,2013.

