基于最小二乘法的机架式服务器机箱下沉量测量方法研究
李欣


摘 要:针对目前机架式服务器机箱负载过重导致的下沉问题设计了一种快速下沉量检测方法,采用最小二乘法构建了基准平面,通过网格线选取测量点生成测量数据,并基于三维曲面图对测量数据进行图形化表达,为生产制造过程提供了管控依据。
关键词:机架式服务器;下沉量测量;最小二乘法;三维曲面图
中图分类号:TB 文献标识码:A doi:10.19311/j.cnki.16723198.2023.02.083
随着互联网、第五代移动通信网络(5th Generation Mobile Networks,5G)技术的发展,企业和个人对网络存储等硬件需求日益增加机架式服务器作为网络存储、虚拟服务重要的硬件设备,其主体结构为U型机箱,主要由镀锌钢板经过多个工序冲压而成。受重力影响,机箱底面会呈现下沉的拱形,多台服务器安装在机柜中,由于下沉会导致相互干涉。服务器下沉量类似于形位公差中的平面度。现阶段衡量服务器下沉量的主流方法是对底面进行平面度检测。但平面度的测量只能量化底面最高点和最低点的极差,无法表现整体下沉趋势。
在平面度检测方面,滕斌等在张昉平面度误差最小二乘法分析的基础上提出了一种基于PLC控制的最小二乘法平面度测量系统设计。在测量误差分析方面,最小二乘法能够准确和充分的处理原始观测数据,且不受测量采样数据点数限制。岳武陵等提出了平面度误差的快速分类法。王傲胜等在此基础上提出了平面度评定的三维曲面构建。目前关于下沉量的研究集中在平面度的测量,而平面度的测量无法直观反映服务器机箱底面的整体下沉趋势。
本文以服务器机箱底面下沉量为研究对象,通过最小二乘法建立数学模型,推导出回归平面作为基准面。根据服务器行业规范推算出允收标准作为服务器下沉量是否合格的依据。对服务器机箱底面以网格线的方式进行快速分区,测量网格线交点到基准面的投影距离。最后输出三维图形,为生产制造过程提供管控依据。
1 机架式服务器下沉量介绍
服务器按照外形结构又分为:机架式服务器、刀片式服务器、塔式服务器等。机架式服务器因其按照统一的工业标准,配合机柜使用,占用空间小。多台机架式服务器可以安装在同一台机柜中,进行集中管理,安全性更高。机架式服务器内部配置有中央处理器、硬盘、主板、电源、风扇以及高速串行计算机扩展总线(Peripheral Component Interconnect Express,PCIE)等模组。
随着功能需求的多样化,PCIE以及硬盘的数量越来越多,一台配置完整的服务器负载重量已经超过50kg。在重力作用下,部署在机柜中的服务器底面会产生如图1所示的下沉。
2 设定基准平面
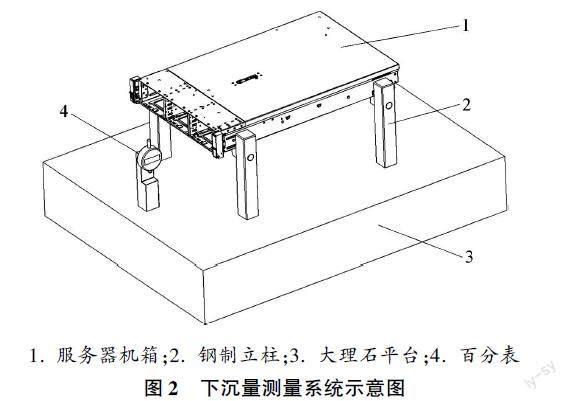
服务器机箱俯视图为矩形,重力作用下导致底面下沉。如图2所示,由钢制立柱、大理石平台、百分表以及服务器机箱组成的测量系统。选取机箱边缘四个顶点作为基准点。将服务器机箱放置于立柱,使用百分表测量基准点。由于三点确定一个平面,受生产误差及重力影响,实际的服务器机箱总会有一点高于另外三点。为了让实际测量误差最小,测量四个基准点的观测值,令其与期望值差的平方和最小。
回歸平面的数学模型推导如下:
Ax+By+Cz+D=0,(C≠0)(1)
式(1)为平面方程的一般表达式,其中A,B,C为常数。又令常数a=-AC,b=-BC,c=-DC,则平面一般方程可改写为:
z=ax+by+c(2)
设服务器底面上四个基准点的位置由xi,yi,zi三个坐标确定。用E表示四个基准点每一取样点的误差和,记为总误差,则式(2)可改写为:
Ei=axi+byi+c-zi(3)
由最小二乘法可知,若使总误差E最小,应使其平方和最小,式(3)可改写为:
E=∑n-1i=0(axi+byi+c-zi)2(4)
若使总误差E最小,分别对a,b,c求偏导数并令其等于0,式(5):
Ek=0,k=a,b,c(5)
根据式(4)和式(5),可推导出式(6)方程组
∑2(axi+byi+c-zi)xi=0∑2(axi+byi+c-zi)yi=0∑2(axi+byi+c-zi)=0(6)
式(6)进行一般数学运算可变换为式(7)
a∑x2i+b∑xiyi+c∑xi=∑xizia∑xiyi+b∑y2i+c∑yi=∑yizia∑xi+b∑yi+cn=∑zi(7)
将式(7)改写为矩阵式:
∑x2i∑xiyi∑xi∑xiyi∑y2i∑yi
∑xi∑yinabc=∑xizi∑yizi∑zi(8)
矩阵经过初等变换为式(9):
abc=∑x2i∑xiyi∑xi∑xiyi∑y2i∑yi∑xi∑yin-1∑xizi∑yizi∑zi(9)
解矩阵式(9)可求得a、b、c,代回式(2)可得到回归平面方程。
3 设定允收标准
U-ENVELOPE是服务器可以占用机架的可用垂直空间量。其中U是服务器行业的专用单位,代表服务器机柜中垂直于机架间的距离,其尺寸由美国电子工业协会(Electronic Association, EIA)所制定,是机架式服务器的标准测量单位,1U约为44.45mm。在机柜上,U表示小腹板中心线之间的距离,用刻度线表示U的开始和结束位置,如图(3)所示。但是,U并不是机架式服务器机箱的实际高度,为了保证尽可能多的内部空间,1U机箱的高度设计高度为42.88mm。令G等于允收标准,则G=44.45-42.882=0.785mm。
服务器机箱下沉量取决于机箱的负载重量。不同于个人计算机,服务器配置可以根据终端用户的需求定制化。行业上从使用功能角度把机箱分成三类:
第一类为空载,此配置仅包含服务器空机箱,不包含任何电子元器件,目的是量化机箱冲压生产制程的稳定。
第二类配置为轻载,此配置为默认出厂配置,仅包含基本的运行和存储功能,通常只包含操作系统用硬盘,中央处理器、主板、散热模块、电源模块等基本电子零件。
第三类配置为满载,即机箱最大负载重量,它配置了全部的可选PCIE扩展卡以及最多的硬盘数量,也可以将其称为极限配置。2U服务器机箱的满载重量约为50kg。不同配置下沉量的允收标准不同,因轻载和满载都会配置于机柜中,且会被终端用户实际使用到。根据上一章节计算出的设计间隙,下沉量在轻载和满载配置下应小于0.785mm。
4 设定网格线
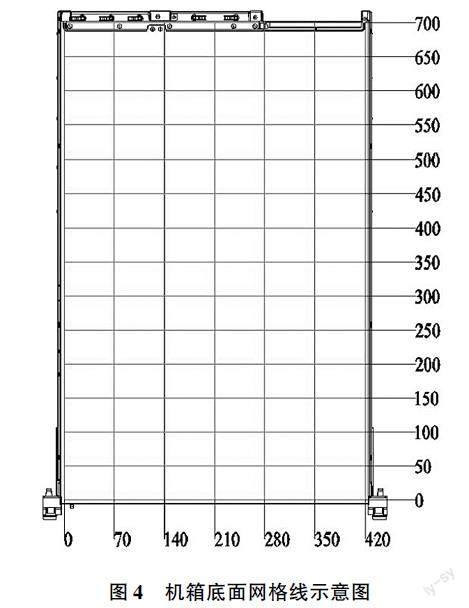
常用品牌机架式服务器机箱长度方向尺寸约为700mm,宽度方向尺寸约为420mm,不同品牌型号服务器尺寸略有差异。因机箱侧墙折弯圆角的影响以及机架式服务器需要预留导轨支撑的空间,起始和结束的网格线距离机箱外边缘保留5mm。如图(4)所示。用记号笔在长度方向从前到后每隔50mm划线,宽度方向每隔70mm划线,长宽两个方向线条的交叉点组成了测量点。
5 输出数据
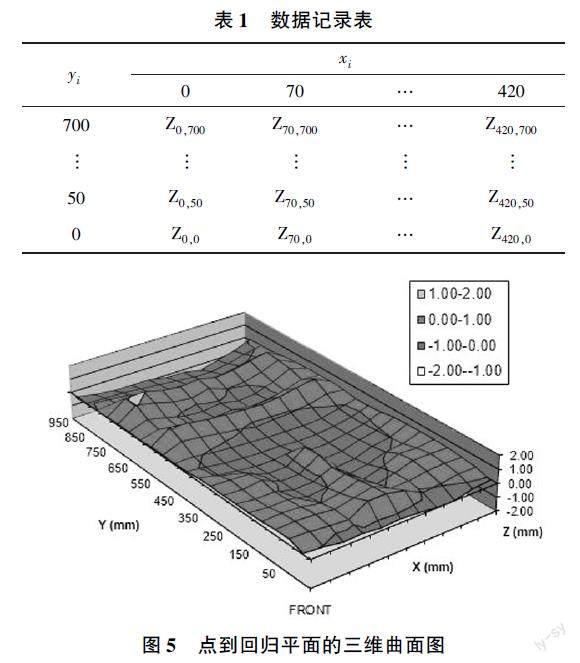
使用百分表对网格线的交叉点按顺序逐一测量,测量到的数据记为zi。其中正数表示测量点高于基准点,负数表示测量点低于基准点,零点表示测量点和基准点重合。将百分表测量数据依坐标填入到表(1)中。
根据数学公式:点到平面距离
d=Axi+Byi+Czi+DA2+B2+C2(10)
将式(2)代入到式(10)可推导出式(11)
d=axi+byi-zi+ca2+b2+1(11)
將表(1)中的原始测量数据代入到式(11)中,可得到一组新的数据,同样记录在新的表(1)中。此表格中的数据表示测量点到回归平面的理论值。表中记录的理论值并不能直观地反映服务器机箱整体的下沉趋势,因此引入三维曲面图。首先,利用EXCEL三维图功能,将表(1)的数据依照坐标生成三维图,然后调整成图(5)的三维曲面图样式。根据不同的下沉量范围设置四种颜色显示,这样可以直观的观测底面整体的下沉趋势以及下沉量超出标准的区域,从而制定针对性的改善措施。最后,通过筛选表格中的数据,找出最低点,如果最低点大于我们的允收标准0.785mm,则该服务器机箱的下沉量不符合要求,判定为不良品,需要进一步分析原因。
6 结论
本文对机架式服务器负载过重导致的下沉问题设计了一种基于最小二乘法的下沉量测量方法。最小二乘法从数理统计学可以充分准确的处理原始观测数据,使四点拟合而成的平面误差最小。根据机架式服务器结构特点建立测量系统并构建数学模型,推导出回归平面作为基准面。对底面划分网格线,取网格线的交点作为测量点,输出测量点到基准平面的数据记录在表格中,最后将数据转换成三维曲面图,为生产制程提供管控依据。
参考文献
[1]谷玉兰,邱国锋,齐元胜,等.基于5G技术的智能制造网络应用场景构建策略[J].数字印刷,2022,8(3):2733,63.
[2]刘升福,吴安,王羽茜.基于尺寸优化的服务器机箱结构优化设计[J].机械设计,2021,38(S1):178182.
[3]滕斌,石安,李天龙.基于PLC控制的最小二乘法的平面度测量系统设计[J].自动化应用,2020,61(10):1113.
[4]张昉.平面度误差的最小二乘法分析[J].机械制造与自动化,2002,31(3):1719.
[5]岳武陵,吴勇,苏俊.平面度误差的快速评定法——测点分类法[J].计量学报,2007,28(1):2933.
[6]王傲胜,杨光.基于最小区域平面度评定的三维曲面构建[J].制造技术与机床,2014,64(6):106109.
[7]张勇.刀片服务器与机架式服务器的比较分析[J].中国教育信息化,2009,15(9):7879.
[8]赵利红,刘树仁,蔡长宁,等.高密度机架式服务器部署设计与实践[J].信息系统工程,2016,29(12):6466.
[9]谢孟晓,刘金祥,牛晓峰,等.数据中心机架式服务器选型对其热环境的影响及优化分析[J].低温与超导,2016,44(8):7478.

