三种电力负荷预测模型的比较

摘 要:负荷预测是电力系统规划、计划、用电、调度等部门的基础工作,电力负荷是影响电网寿命和可靠度的一个重要因素。文章结合某电网近年的电力负荷所给出的数据,分别运用灰色GM(1,1)预测模型、小波神经网络模型和随机森林模型对电力负荷进行预测,比较模型的优缺点。
关键词:灰色模型;小波神经网络;随机森林模型
中图分类号:TM715 文献标识码:A 文章编号:1006-8937(2016)27-0053-02
电力系统数字仿真已成为电力系统规划设计、调度运行和试验研究的主要工具,大量研究结果表明,负荷特性对电力系统分析计算结果具有重要影响,不同的负荷模型对电力系统的仿真计算都有不同的结果。因此,准确的负荷预测,既可以保持电网运行的安全稳定性,又能够有效降低发电成本,提高社会效益和经济效益。
负荷预测的核心问题是预测方法的使用,现代科学技术在不断发展和进步,负荷预测建模技术相关理论研究不断深入,有关技术取得很大进步,对建模方法的探索,一直是国内外学者所关注的热点,本文基于用户用电量和电负荷量这两个主要指标,结合天气温度、季节、经济增长和人口变化等因素,利用灰色预测、小波神经网络模型、随机森林模型三种方法,较为合理的预测了用户未来的电量及电负荷量,取得了较好的预测效果。
1 灰色预测模型
3 随机森林模型
随机森林模型是一种组合分类器,它在基于统计学习理论基础上,将决策树算法与bootstrap重抽样方法相结合,首先构造一个集合,基于树型分类器,然后使用该集合通过投票进行分类与预测。
4 仿真预测
根据电网的数据,分别建立灰色GM(1,1)模型,小波神经网络模型和随机森林模型,并对所得结果进行检验。
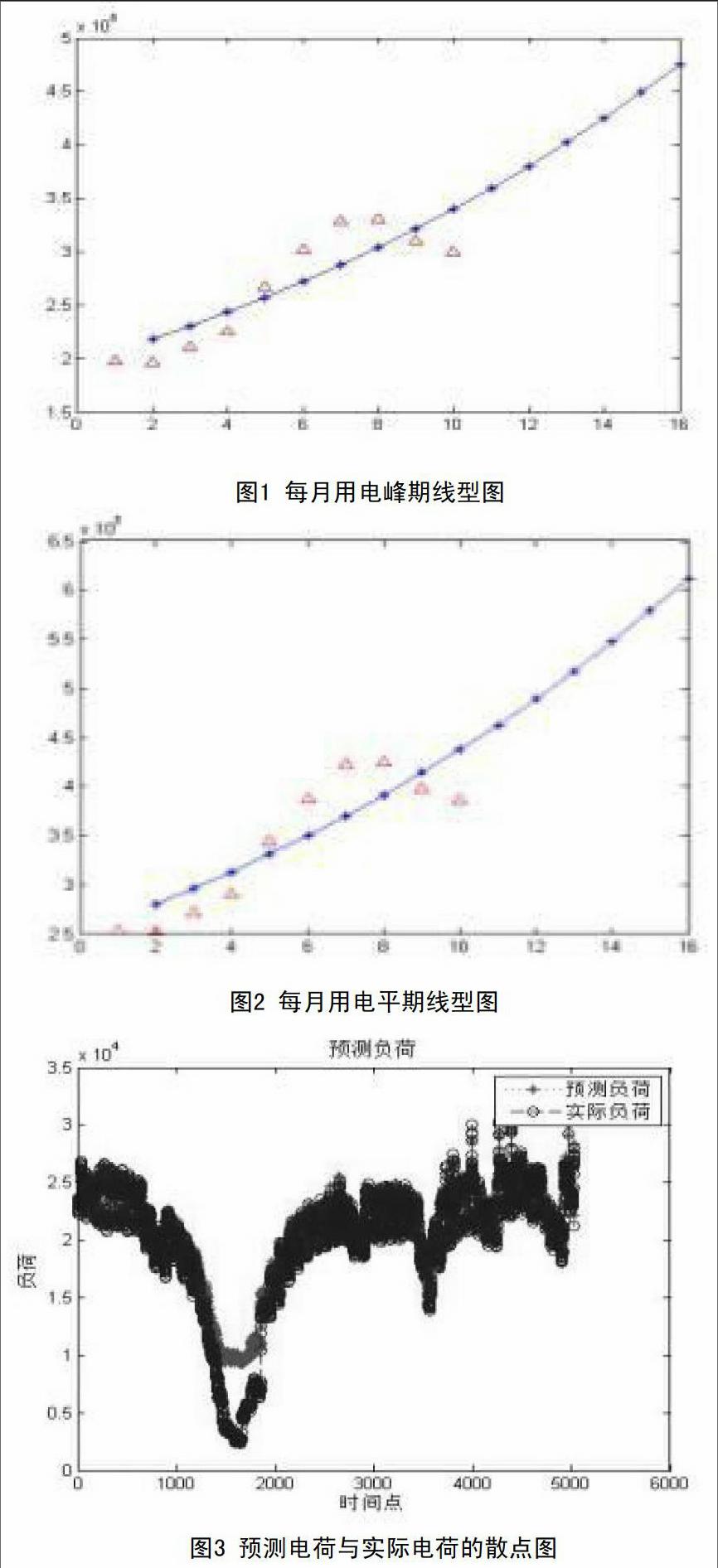
针对模型1,首先我们通过分析处理了异常数据,再使用累加法生成了累加生成序列,然后建立GM(1.1)灰微分方程模型。最后运用MATLAB求出对应的白微分方程、进行残差检验、并求出预测值,所得结果如图1和图2所示。
针对模型2,首先整理数据,尤其是对神经网络中的输入,输出参数要进行统一的线性变换,这样就可以避免模型失败因为由于数据基准的不同,可能导致学习过程不收敛。再对处理后的数据进行规范化计算,取最小-最大的方法,对计算得到的数据进行标准化数据还原。然后编写MATLAB程序,对处理后的数据进行计算。考虑到主变1和主变2是影响和决定总表的因素,将其作为输入变量;总表是一个连续物理变量,时序性强,因此将其历史数据也作为输入变量。将t时刻主变1、主变2、和主表的前n个历史数据(t-n+1,t-n+2,…,t+1时刻总表数据)作为输入,输出分别为t时刻主变1、主变2和总表。将对总表的数据进行预测,然后再把主变1、主变2的预测结果对总表进行拟合。多次实验,得到当n=4时,结果误差最小。最后生成预测数据与实际数据的散点图,如图3所示。
针对模型3,采取步骤:
第一步:将记录所有数据,看作是一个节点;
第二步:寻找每个变量的各种分割方式,找出最好的分割点;
第三步:运用分割点将记录分割成两个子结点C1和C2;
第四步:对子结点C1和C2重复执行步骤Step2、Step3,直到满足特定条件为止。
将每个时间段看作是一个节点,每隔15分钟,划分一个空间。决策树的分割点就是各种因素,记录子节点C1和C2。重复执行直至结果在可接受误差之内。
5 模型优缺点比较
5.1 灰色预测模型
模型优点:不需要考虑数据的分布规律,变化趋势,同时运算比较方便,若用于短期预测,精度比较高,并且所需要的电力负荷数据少,对结果检验非常方便。
模型缺点:只适用于原始数据具有良好光滑性能的中长期预测,局限性体现在以下方面:①数据离散程度越大时,预测精度就越差;②不太适合对电力负荷进行中长期预测,特别是长期后推若干年的预测[3]。
5.2 小波神经网络模型
模型优点:小波神经网络可以避免MLP神经网络结构设计的盲目性;可以从根本上避免局部最优等非线性优化问题,因为学习目标函数的凸性,网络权系数的线性分布;
模型缺点: 随着网络的复杂度增加呈几何级数增长趋势,训练时所需的网络隐含层较多,而且时间和迭代次数较多。
5.3 随机森林模型
模型优点:对于很多种不同数据,可以处理数据量较大的变量输入,并且产生准确度高的分类器。在内部可以产生不偏差的估计对于一般化误差后,在建造森林时。对于数据的挖掘、侦测的偏离和资料视觉化等方面非常有用,在计算亲近度时。在决定类别时,评估变量的重要性。可被继续应用在使用非监督聚类的未标记的资料上。学习过程非常快速,同时在决定类别时,评估变量的重要性。
模型缺点: 在搜索中不进行回溯,所以它容易收敛到非全局的局部最优解;在学习中,由于分类器比较复杂,会过于适应噪声,可能会导致过拟合的问题[4]。
6 进一步的讨论
近十几年来,随着科技的发展,预测模型取得了深远的进步。不断涌现出新的模型,为提高预测模型的精准度,需要进一步使用组合预测。
组合预测有两种方法:①对于几种预测模型得到的预测结果,选取适当的权重进行加权平均运算;②在几种预测模型结果中进行比较,选取拟合优度最佳的预测模型作为最优方法进行预测。通过组合预测在大多数情况下,可以达到改善预测结果的目的。
参考文献:
[1] 梅正阳,韩志斌.数学建模教程[M].北京:科学出版社,2012.
[2] 陈哲,冯天瑾,陈刚.一种基BP算法学习的小波神经网络[J].青岛海洋大 学学报,2001,31(1):122-128.
[3] 朱祥和.两种短期电力负荷预测模型的比较[J].黄冈师范学院学报, 2012,(3).
[4] 张焰,田世明.采用互信息与随机森林算法的用户用电关联因素辨识 及用电量预测方法[J].中国电机工程学报,2016,36,(3):604-614.

