基于粒子群算法优化参数的VMD-GRU短期电力负荷预测模型

徐 岩，向益锋，马天祥

(1.华北电力大学 电气与电子工程学院，河北 保定 071003；2.国网河北省电力有限公司电力科学研究院，河北 石家庄 050021)

0 引 言

负荷预测在制定供电计划和实现电网电量供需平衡中发挥着越来越重要的作用，精确的电力负荷预测可指导一个地区电力系统发展策划，为电网可靠运行提供安全保障以及减小运行成本[1]，也为现行市场下电网编制调度计划、营销计划和供电计划提供信赖依据。电力系统负荷预测根据时间可分为超短期、短期、中期和长期预测[2]。提高短期电力负荷预测准确性，有助于缓解供需两端不平衡，显著提升电力设备利用率，降低能耗。在另一方面，随着电网持续扩建，电气设备接入增多，信息化程度不断提高，智能电网采集数据愈来愈精准，为负荷预测提供可靠、海量数据，利于深度学习的应用。

电力负荷预测准确性受到多个因素影响，得到绝对预测方法较为困难，提升预测模型准确性显得尤为重要。现阶段，考虑到负荷序列具有时序性和非线性特点，国内外学者为此展开大量深入研究，由简到繁的提出了多种模型，多元线性回归法[3]结构简单，但预测精度较低；卡尔曼滤波算法[4]较好解决数据中噪声问题但也会滤除变化较大的负荷对结果造成误差；灰色理论[5]所需数据量较少，计算简便，但相关因素联系考虑不足；支持向量机[6](Support Vector Machine)预测精度较高但其预测时间较长，大规模预测较为困难；随机森林法[7]可处理高维数数据，泛化误差小，但对高噪声数据容易出现过拟合的情况；以及近阶段运用较为广泛的神经网络算法[8，9]等。随着深度学习逐渐兴起，深度学习在负荷预测领域应用愈来愈广泛，文献[10-12]将长短期记忆网络(Long Short-term Memory,LSTM)运用负荷预测中，网络深度和宽度均可改变，预训练有效解决传统网络产生局部最优解问题。门控循环单元(Gated Recurrent Unit,GRU)神经网络作为LSTM的一种变体能够简化门控结构提高网络收敛速度的同时保证时序预测性能[13，14]。

对于随机性波动性较强负荷序列，单一预测方法往往难以达到理想的负荷预测精度。当前，各种组合预测方法在短期负荷预测领域应用较为广泛，以经验模态分解(Empirical Modal Decomposition，EMD)为主[15]的分解方法能实现原始负荷序列的分解，实现平稳序列与非平稳序列的分离，但分解出的各分量易出现模态混叠现象，影响最后的预测精度。文章[16]提出一种基于集总经验模式分解(Ensemble Empirical Mode Decomposition，EEMD)和Elman神经网络的短期负荷预测方法，在分解前加入高斯白噪声，可有效改善EMD模式分解的模态混叠现象，但因其采用递归方法的求解模式处理原信号，对测量噪声的鲁棒性有待加强。文[17]应用变分模态分解(Variational Mode Decomposition,VMD)将数据分解不同特征的模态函数，有效避免模态混叠现象，使得信号分析效果更好。负荷序列分解效果受模态分量个数k和惩罚参数α影响，在电力负荷预测领域，这俩个参数的确定缺乏一个较科学的评价标准，存在经验性与主观性，影响到负荷序列分解效果和最后的负荷预测精度。

鉴于此，本文考虑提出一种基于粒子群算法优化参数的VMD-GRU短期电力负荷预测模型。为了从原始含噪声较多的负荷序列中提取包含丰富特征信息的信号分量，实现最佳信号处理效果，本文先通过粒子群算法对VMD算法最佳影响参数组合进行搜寻，得到最佳效果的分解子序列，减少不同趋势信息对预测精度影响。然后运用GRU算法，针对各子序列分量建立基于GRU的预测模型。最后叠加各子序列预测结果得到短期电力负荷的最终预测值。结合仿真案例，结果表明，相较于其他预测算法，所提算法具有更高的预测精度，能更好地预测电力负荷未来短期变化趋势。

1 基于粒子群算法参数优化改进的 VMD-GRU短期电力负荷预测模型

1.1 变分模态分解

作为技术相对成熟且理论较为完备的信号分解技术，变分模态分解(VMD)有效避免了EMD和EEMD等方法在分解过程中遇到的模态混叠及端点效应的情况，可用以获得更平稳的负荷序列[18]。运用VMD技术可以减弱相当大部分噪声，降低信号的非平稳性，然后分解得到多组具有固有模态函数(IMF)。假定待处理原始负荷序列为f(t)，运用VMD进行信号分解的约束表达式定义如下：

(1)

上式中：{uk}、{ωk}为分解后第k个模态分量表达式和中心频率；参数K是模态分解个数；δ(t)代表狄克拉函数；*为卷积操作符；分解所得所有模态分量与原负荷序列f(t)一致。运用Lagrange算子解决上述问题，公式(1)更新如下：

L({uk},{ωk},λ)=

(2)

式中：λ为Lagrange算子；α是二次惩罚因子。运用ADMM寻优迭代后可得到模态分量uk，可求出各自的模态频率ωk和Lagrange算子λ表达式如公式(3)～(5)。

(3)

(4)

(5)

1.2 基于粒子群优化参数的变分模态分解

由于VMD与EMD 建立的理论框架有所不同，二者存在诸多差异，VMD在进行信号分解时需要预先设定IMF分解的个数，不同的分解个数会对最终处理结果造成不同的影响，国内外研究发现VMD算法中的惩罚参数α会对分解结果造成较大影响，α越大，所得IMF分量带宽越小，相反，信号带宽越大。实际待分析负荷序列信号变化较为复杂，上述俩参数通常难以确定，如何选取适当的参数是处理原始负荷序列的关键所在。

如果独立的讨论两参数的影响，一个参数不变，对另一个参数展开优化，讨论此参数对结果的影响，此种方式往往较难考虑到两参数间的交互作用，所得到解往往为相对最优解。作为一种群体智能优化算法，粒子群算法[19]具有较好的全局寻优能力，本文运用粒子群算法对VMD算法两个影响参数进行同步寻优，避免主观因素对参数选取的干预，智能选取出最佳参数组合。

假设在一个D维空间中，由M个粒子组成种群X=(X1,X2,…,XM),第i个粒子在D维空间里的位置为Xi=(Xi1,…,XiD)(对于优化问题的潜在解)，第i个粒子速度为Vi=(vi1,vi2,…,viD),个体局部极值为pi=(pi1,pi2,…,piD)，整个种群全体极值G=(g1,g2,…,gD)，每个粒子通过个体局部极值和种群全部极值更新迭代自身位置和速度[20，21]。

(6)

式中：w为惯性权重；d=1,2,…,D;i=1,2,…,M;k为当前迭代次数；c1、c2是加速度因子，η为[0,1]之间随机数。

在利用粒子群算法搜寻VMD算法影响参数时，确定好恰当的适应度函数，粒子每更新其位置时就计算一次新的适应度值，通过对适应度值的对比实现更新。Shannon熵为一种较好反应信号稀疏性的标准，其值大小反映概率分布均匀性，等概率分布(不确定性最强的概率分布)熵值较大[22]。本文在此基础上提出包络熵的概念，将一个概率分布序列pj视作由信号解调运算得到的包络信号处理而成，由它计算得到的值体现原始负荷序列稀疏特性。零均值信号包络熵可用如下式表示：

(7)

式中：pj为a(j)归一化形式；x(j)经Hilbert解调后得到的包络信号为a(j)。

原始负荷序列信号经过VMD处理之后，若其分解得到的IMF分量噪声信号较多，则分量信号的稀疏性不够强，包络熵值不够大。反之，若IMF分量包含原始负荷序列特征信息较多，则其包络熵值较低。计算粒子于一处位置(对应一组参数组合α和K)由VMD分解得到所有的IMF分量包络熵值，并取所有当中最小的一个为局部极小熵值，记作minLEpIMF，与此值相对应分量即为包含负荷序列局部特征信息最佳的分量，本文将适应度值设定为寻优过程中出现的局部极小熵值，最小化此值作为最佳寻优目标，则α和K优化步骤如图1。

1.3 门控循环单元神经网络GRU

GRU作为RNN的变体之一，而电力负荷具有周期性规律，其能够较好捕获时间序列长短期之间依赖关系，能够解决复杂环影响下的电力负荷预测问题，GRU模型如图2。

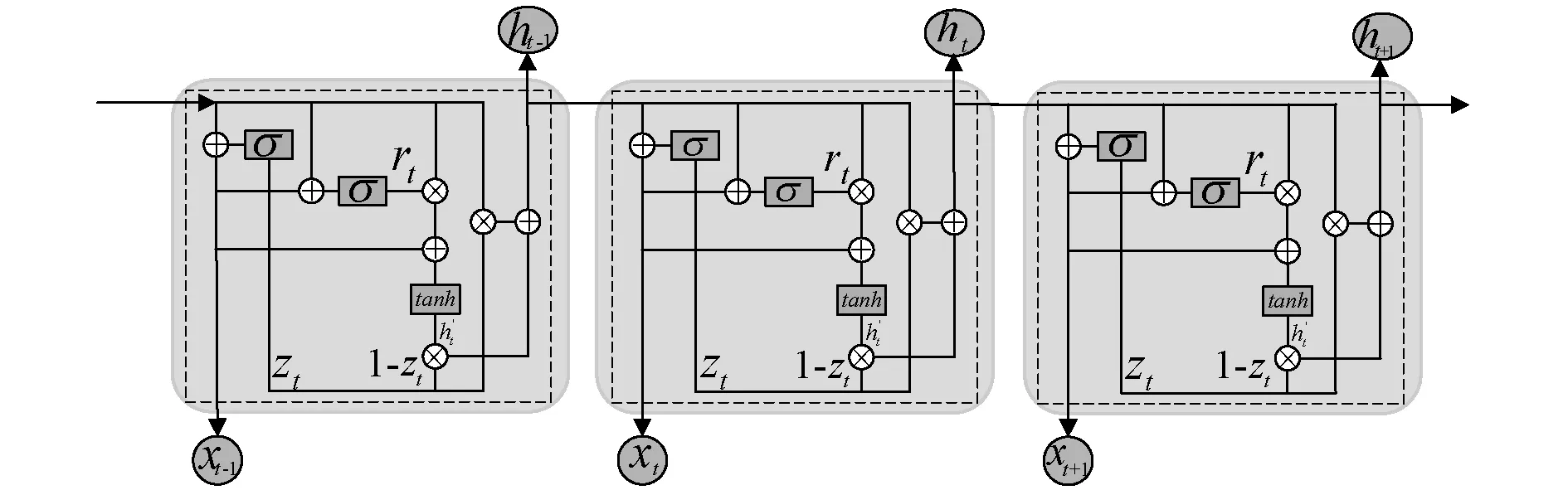
图2 GRU网络结构Fig.2 GRU network structure

其内部逻辑结构关系公式如(8)～(11)：

zt=σ(W(z)xt+U(z)ht-1)

(8)

rt=σ(W(r)xt+U(r)ht-1)

(9)

(10)

(11)

式中：更新门与重置门输入量权重矩阵分别用W(z)、W(r)表示；更新门与上一时刻重置门记忆内容权重矩阵。“×”是矩阵Hadamard积，加减法运算用“±”表示，sigmoid及双曲正切函数由σ和tanh，输入、更新和重置门由xt，zt和rt，h′t为之前记忆内容，ht为当下时间步终时记忆。

1.4 基于粒子群算法改进参数优化的VMD-GRU电力负荷预测模型

为进一步提升短期电力负荷预测的准确性，由于电力负荷序列具有非线性和非平稳性的特点，考虑到变分模态分解技术在序列平稳化处理和信号去噪等领域显著优势、门控神经网络在时序数据预测的突出表现以及粒子群算法在参数优化方面的优良性能，本文提出一种基于粒子群算法改进参数优化的VMD-GRU短期电力负荷预测模型，通过智能选取出VMD最佳参数组合，得到最佳分解效果子序列，有效减弱电力负荷序列非线性，更好地提取负荷序列特征信息，减小负荷预测难度，有效提升电力负荷预测精度。本文所建立的组合预测模型实现步骤如下：

1)粒子群算法优化参数的变分模态分解。对于收集到的电力负荷时间序列数据，运用粒子群算法对VMD算法两个影响参数进行同步寻优，智能选取出最佳参数组合，得到一组最优IMF分量，对各分量进行归一化。

2)训练及测试样本划分。数据集划分如图3所示，多个训练样本由步长为1 的滚动窗口将训练样本进行划分得来，样本输入为X=[X1，X2，…，Xl]，待预测数据P=[Xl+1，Xl+2，…，Xl+S]，通过样本对结果进行评估。

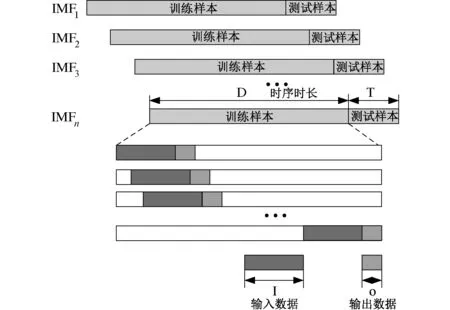
图3 训练与测试数据集划分Fig.3 Training and test data set division

3)对2)分解出的各子序列运用GRU网络进行预测，构建基于GRU 的预测模型，并运用Adam算法调整迭代过程中的权重。

4)负荷预测。对经过优化参数后的最佳预测模型分别进行预测，叠加各IMF预测结果得到最终电力负荷预测值。

5)评估预测结果。与真实电力负荷数据进行对比，通过相应的评估指标评价模型实际预测效果。

整体预测框架如图4所示。

图4 整体预测框架结构Fig.4 Overall forecasting framework structure

2 实验分析与结果展示

2.1 数据集及数据预处理

数据集选用丹麦西部2016年(2016年4月1日至2016年5月31日)负荷数据，采样间隔为30分钟一个点，每天取48个点，每类有2928条数据。为便于模型训练，本文对所选数据进行归一化处理，具体如式(12)：

(12)

式中：x是原始值，极大值和极小值分别用xmax和xmin表示。

对归一化负荷数据进行展示，图可看出电力负荷波动频繁，峰谷值范围并不具体，可见该负荷数据周期性较差，还包含大量噪声等。

选取该数据集中前2 928个点54天内的数据作为训练集，后336个点7天内的数据进行测试，在训练集中取前n个点对应n+1的点，即[x1,x2,x3…xn]对应xn+1，[x2,x3,x4…xn+1]对应xn+2，依次对训练集进行分割，测试集也做同样处理。

2.2 误差评估指标

预测结果误差评估指标[]采用平均绝对百分误差(Mean Absolute Percent Error,MAPE)和均方根误差(Root Mean Square Error,RMSE)，公式如式(13)和(14)。

(13)

(14)

式中：yl为预测值，yi为实际值，n为样本数量。

2.3 VMD算法重要参数的选取

通过前述VMD模型可知，在VMD算法当中分解尺度K以及惩罚因子α是影响分解效果的关键参数。分解尺度K过大，则同一频率特性的模态分量会分解到不同模态分量中，导致模态共享现象，若分解尺度K过小，则负荷序列信息不能完整表达，会缺失大量频率细节。惩罚因子α影响到分解后模态分量带宽，二者呈反比关系，研究表明，模态分量带宽越小，越可改善分解结果模态混叠问题，表1反映不同模型参数对分解效果影响。

表1 K取值及α取值对VMD影响Tab.1 Value K&αand the impact on VMD

当前，VMD参数未有科学客观选取方法，反复实验成为大多数研究学者确定分解尺度的方法，在合理范围内，固定惩罚因子及其他参数，逐步增加分解尺度取值，使VMD分解出相应数量模态分量，观察每个模态分量中心频率，看有无模态混叠或者模态共享现象出现，以此确定分解尺度取值。

将惩罚因子α值定为2 000，取样间隔为30分钟，T=0.5,取K=3,4,5,…,11,各模态分解后的中心频率如表2所示，据其确定合适的K值。

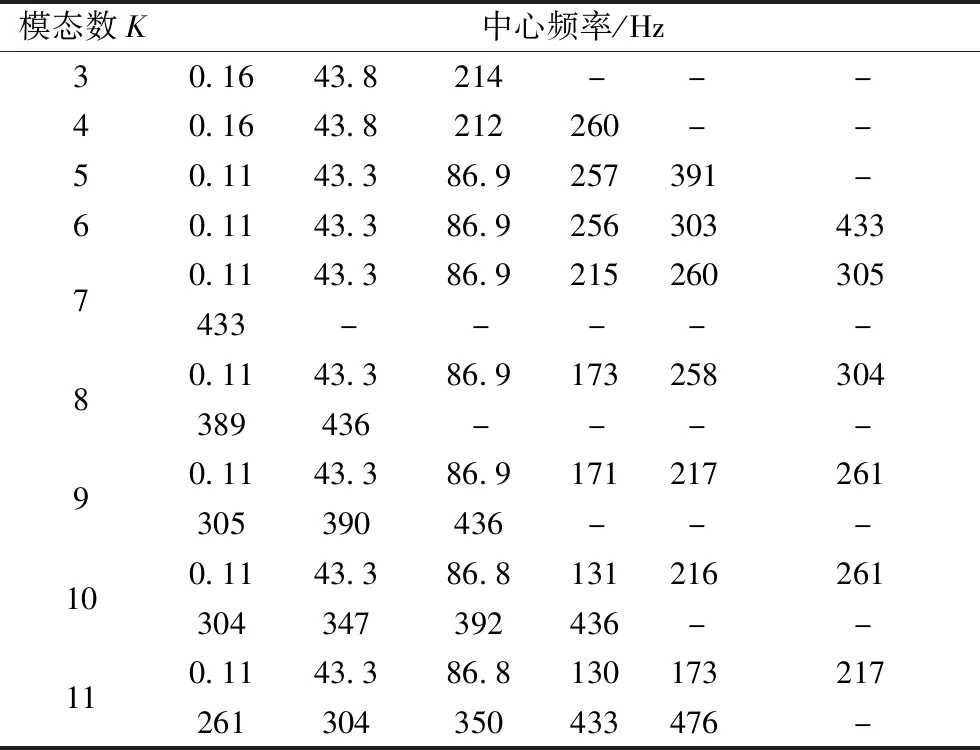
表2 不同模态数中心频率Tab.2 Center frequency of different modal numbers

从表2可得当模态数取3～6时还有相关细节分量信息没能完全分解，原始负荷序列有相当信息被忽略，当模态数为8时，模态5和模态6中心频率接近，模态7和模态8中心频率接近；当模态数为9时，模态4和模态5以及模态6与模态7中心频率接近，同相差约40 Hz，当分解模态数为10和11时，分解愈加过度，不同分量中相似的中心频率更多，模态共享现象较为明显。综合分析，负荷序列的分解尺度应该选为7较为合理。

惩罚因子选取和分解后各模态分量带宽成反比关系，为了避免结果中出现模态混叠现象，α不宜过大，另一方面，α值也影响VMD分解速度，固定其他参数来选取惩罚因子参数，不同惩罚因子数值对应VMD分解结果如表3所示。

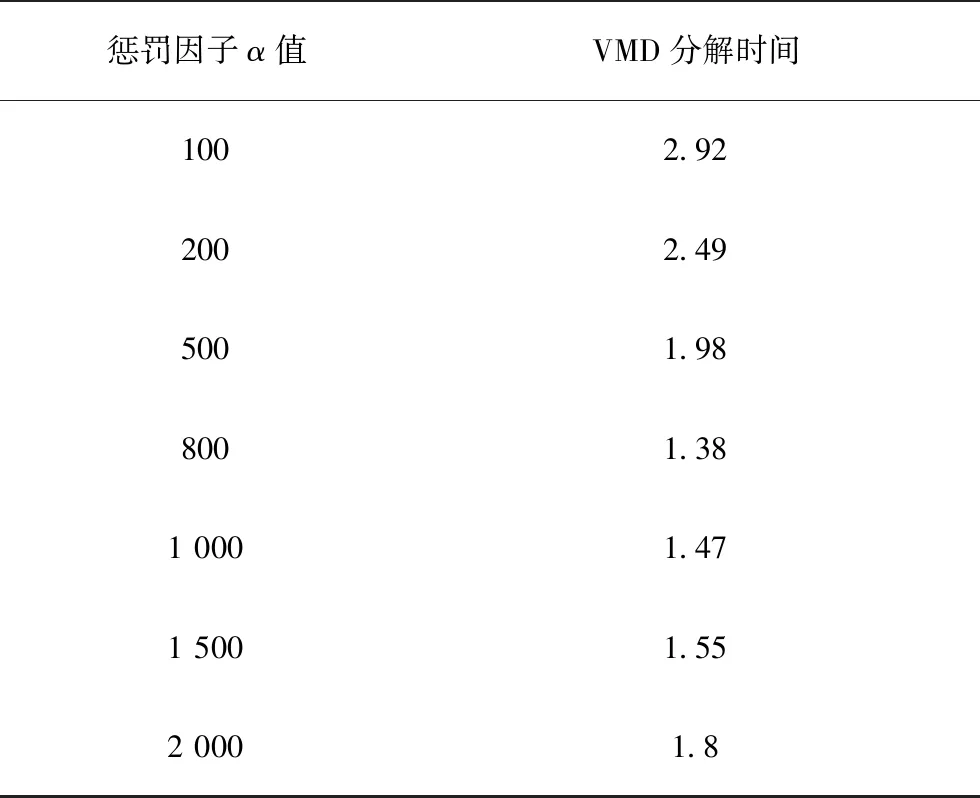
表3 不同惩罚因子对应分解结果Tab.3 Different penalty factors corresponding to decomposition results

由表3可知，α值在800附近时，VMD算法运算时间最短，当取值超过800时，运算时间逐步延长，可得随着惩罚因子取值的增大，整个模型消耗时间呈先增大后减小趋势，另一方面，α值越高发生模态混叠的可能性越低，综上惩罚因子取1 000较为合适。

2.4 粒子群优化参数的VMD负荷分解

运用粒子群算法搜寻VMD算法的最佳参数α和K，设定粒子群算法初始参数如表4所示，Gmax代表最大进化代数，M为种群规模。

表4 粒子群算法各项参数Tab.4 Various parameters of particle swarm algorithm

运用粒子群算法进行参数寻优，过程中的局部极小值熵随着种群进化代数变化如图，由图易得局部熵最小值经过一次迭代后到达最小值1.41，并保持不变，搜索到的最佳参数组合[K0,α0]=[8,200],保真度系数和收敛停止条件在这里取默认值，τ=0.3，ε=10-7运用粒子群算法进行参数优化后的变分模态算法对负荷序列进行处理，得到VMD分解图及模态分解频谱图如图5。

图5 局部极小值熵进化代数变化Fig.5 Local minimum entropy evolution algebraic change

从图6～7可以观察到原始负荷序列稳定性差、波动和随机性极强，从分解图可看出从IMF1～IMF8各模态振动幅度逐渐减小，这些IMF分量均包含原信号不同时间尺度局部特征信号，频谱分解图表明分解效果极佳，没有模态混叠现象出现，各模态分 量频带均在中心频率周围，结果可得，经过粒子群算法参数优化的变分模态分解能较好提取负荷序列中特性子序列，为更高精度负荷预测打下坚实基础。

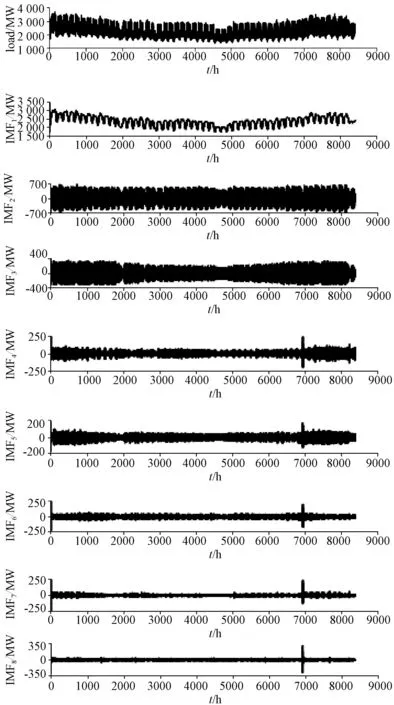
图6 VMD分解图Fig.6 VMD decomposition

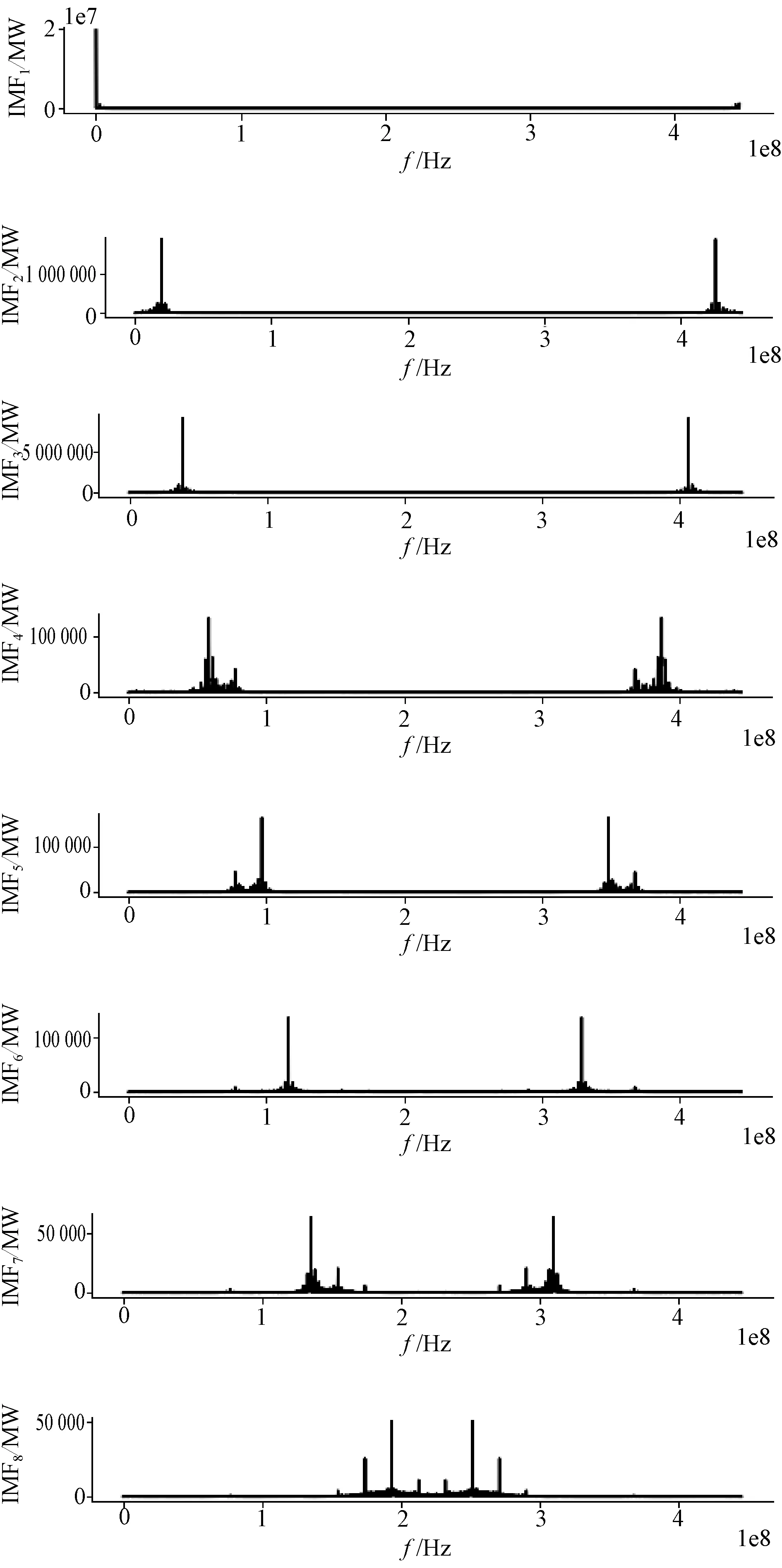
图7 模态分解频谱图Fig.7 Modal decomposition spectrogram

2.5 GRU网络参数选取

根据本文提出的粒子群优化参数的VMD-GRU负荷预测模型，利用2016年丹麦西部4～5月用电负荷数据进行仿真，固定GRU参数，对GRU网络层数选取进行调整，通过MAPE和RMSE大小来判断预测精度，仿真结果如表所示。从表5可以看出，适当增加GRU层数可以提高负荷预测精度，而当层数超过2时，出现了过拟合的情况，据此，本文将GRU 层数定为2层。确定好GRU层数为2之后，将神经元数量设置为2n，随后固定GRU层数、训练轮数和批次，改变n的取值，通过MAPE大小来判断预测精度，经过对比将GRU网络神经元数量设为64，返回全部时间步的隐藏状态；为减少数据流，降低冗余特征的干扰，第二层设置为32，返回全部时间步的隐藏状态。

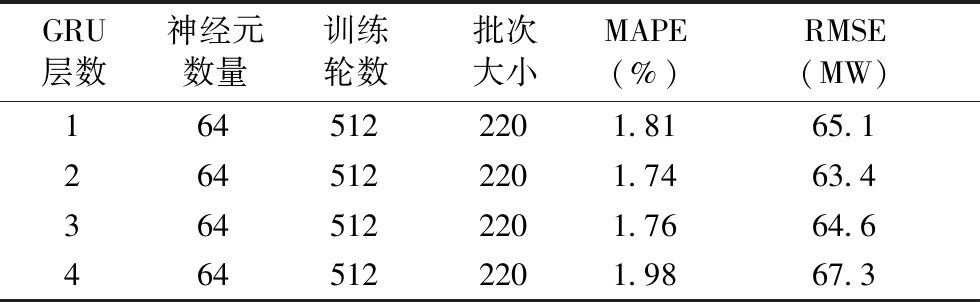
表5 GRU层数调整结果Tab.5 GRU layer adjustment result

2.6 预测结果对比

分别利用BP神经网络、SVR、GRU、EMD-GRU及VMD-GRU和PSO优化VMD-GRU进行仿真实验，对各网络模型参数进行调优，运用相同的训练集进行训练。确定好各个模型的参数后，以相同的测试集预测2016年中的一个星期(5月25日至5月31日)的电力负荷，计算其MAPE及RMSE和训练时间，结果如表6所示。仿真结果如图8所示，结果说明门控循环网络在一天及一个星期的MAPE及RMSE为2.81%和91 MW、2.02%和67.2 MW。较BP神经网络和SVR有更高的预测精度，运用EMD能将负荷序列平稳化处理，将分解的IMF单独预测，可以互不干扰，降低预测难度，可观察到EMD-GRU预测精度较GRU有较大提升，MAPE和RMSE分别降低0.96%和7.5 MW，图为上述模型在2016年5月30日负荷预测结果曲线，可明显看出BP和SVR在波峰和波谷区域出现较大幅度偏差，而GRU和EMD-GRU相对于这两种模型都能较好地与真实曲线拟合。分析GRU与EMD-GRU模型的负荷预测曲线，从整体上看基于EMD-GRU模型的预测曲线不仅在波峰波谷区域与实际变化曲线更贴近，在其他区域也与实际变化趋势更加吻合，其原因为序列的非平稳性导致GRU不能很好的预测序列变化趋势，而EMD重构则较好改善这一问题，提高了负荷预测精度。而变分模态分解VMD有效改善EMD存在的模态混叠及端点效应的问题，提升分解效果，VMD-GRU模型较EMD-GRU预测模型24 h内MAPE和RMSE分别降低0.44%和16.2 MW。经粒子群算法优化参数后的变分模态分解更好的提取出了原始负荷序列的子序列，使其得到一组包含更多原始序列特征信息的模态分量，进一步提高了预测精度，经粒子群优化参数的VMD-GRU模型24 h内其MAPE和RMSE较VMD-GRU分别降低了0.99%和24.7 MW，而168 h内其MAPE和RMSE较VMD-GRU分别降低1.15%和36.2 MW，可以得到经PSO优化的VMD-GRU算法显著提高了负荷预测精度，使得预测结果更贴近真实曲线。

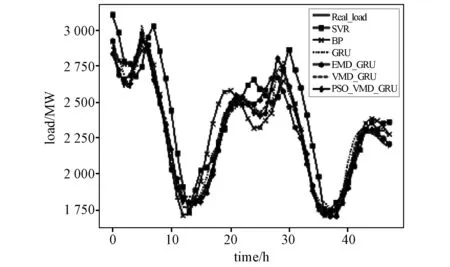
图8 不同模型的预测曲线图Fig.8 Forecast curves of different models

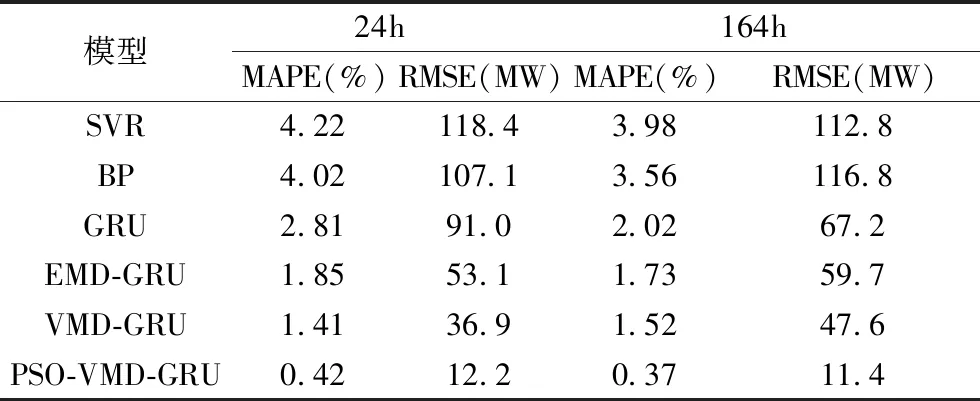
表6 不同预测模型预测结果对比Tab.6 Comparison of prediction results of different prediction models

3 结 论

面对日益提高的电力系统负荷预测精度的需要，本文提出一种经PSO优化参数的VMD-GRU电力负荷预测模型。为了从原始含噪声较多的负荷序列中提取包含丰富特征信息的信号分量，实现最佳信号处理效果，本文先通过粒子群算法对VMD最佳影响参数组合进行搜寻，得到最佳效果的分解子序列，减少不同趋势信息对预测精度影响。然后运用GRU算法，针对各子序列分量建立基于GRU的预测模型。最后叠加各子序列预测结果得到短期电力负荷的最终预测值。经PSO优化参数的VMD-GRU模型的短期电力负荷预测优势如下：

(1)此模型结合了粒子群算法、VMD和GRU网络各自特点，发挥出各自优势，实验结果表明该模型可明显提升短期电力负荷预测精度。

(2)运用粒子群算法对影响VMD算法的两大参数分解尺度和惩罚因子进行寻优，得到最佳分解效果子序列，避免了人为主观与经验性影响，进一步提高负荷预测精度。