土壤有效养分测定值与其校正系数的函数关系选择

蒋琳， 迟春明

(塔里木大学农学院 塔里木大学南疆绿洲农业资源与环境研究中心，新疆 阿拉尔 843300)

我国农作物推荐施肥方法可概括为测土施肥法、效应函数法和营养诊断法三大体系[1]。测土施肥法综合考虑作物目标产量养分需求量、土壤养分供应量、肥料养分利用率等多方面因素，是一种科学合理的平衡施肥方法，在生产实践中得到了广泛应用[1-2]。该方法最早由美国土壤学家Truog于1960年提出，1967年Ramamoorthy等在印度推广应用[3]。20世纪80年代初上海化工学院根据印度文献将该方法引入我国[4]，使用“土壤有效养分校正系数”与土壤有效养分测定值的乘积计算土壤养分供应量，以解决田间试验测定土壤养分供应量存在的耗时耗力问题。该方法在实践应用中不断完善，促进了土壤有效养分校正系数相关研究的发展[5-8]。土壤有效养分校正系数并非恒定值[5,8]，而是随土壤有效养分测定值、作物类型等的变化而改变[9-10]。为了提高土壤有效养分校正系数在应用中的准确性，各地建立了不同作物栽培条件下土壤有效养分校正系数与土壤有效养分测定值之间的函数关系方程[1,10-14]。函数关系方程的形式主要有线性方程[15-16]、对数方程[9,17]、双曲线方程[10,18]和幂函数方程[19-20]等。这些函数方程(校正系数方程)一般都具有较高的拟合度。但已有研究结果多数情况是直接给出选用的某种函数形式，鲜有将校正系数推算值与实测值进行比较分析，因此，根据校正系数方程推算的校正系数其准确性如何需进一步研究；同时，校正系数方程与土壤有效养分测定值相乘即为土壤养分供应量估算值随土壤有效养分测定值的变化关系曲线，其与实际情况是否相符仍需进一步研究。本文针对这2个问题开展研究，以期为土壤有效养分校正系数的准确应用提供借鉴。

1 材料与方法

采用柏琼芝等[19]土壤碱解氮、有效磷、有效钾测定值及其校正系数的试验数据进行分析。分别采用对数函数、双曲线函数和幂函数3种形式构建土壤有效养分测定值与其校正系数的归回关系曲线。通过决定系数(R2)和均方根误差(RSME)的大小判断回归关系曲线的拟合度。

将校正系数方程与土壤有效养分测定值相乘得到土壤养分供应量的估算值，建立其与土壤有效养分测定值的回归关系曲线，分析土壤养分供应量估算值随土壤有效养分测定值的变化规律。

2 结果与分析

2.1 土壤有效养分测定值与其校正系数的关系

土壤氮、磷、钾有效养分校正系数随其测定值的变化趋势见图1。

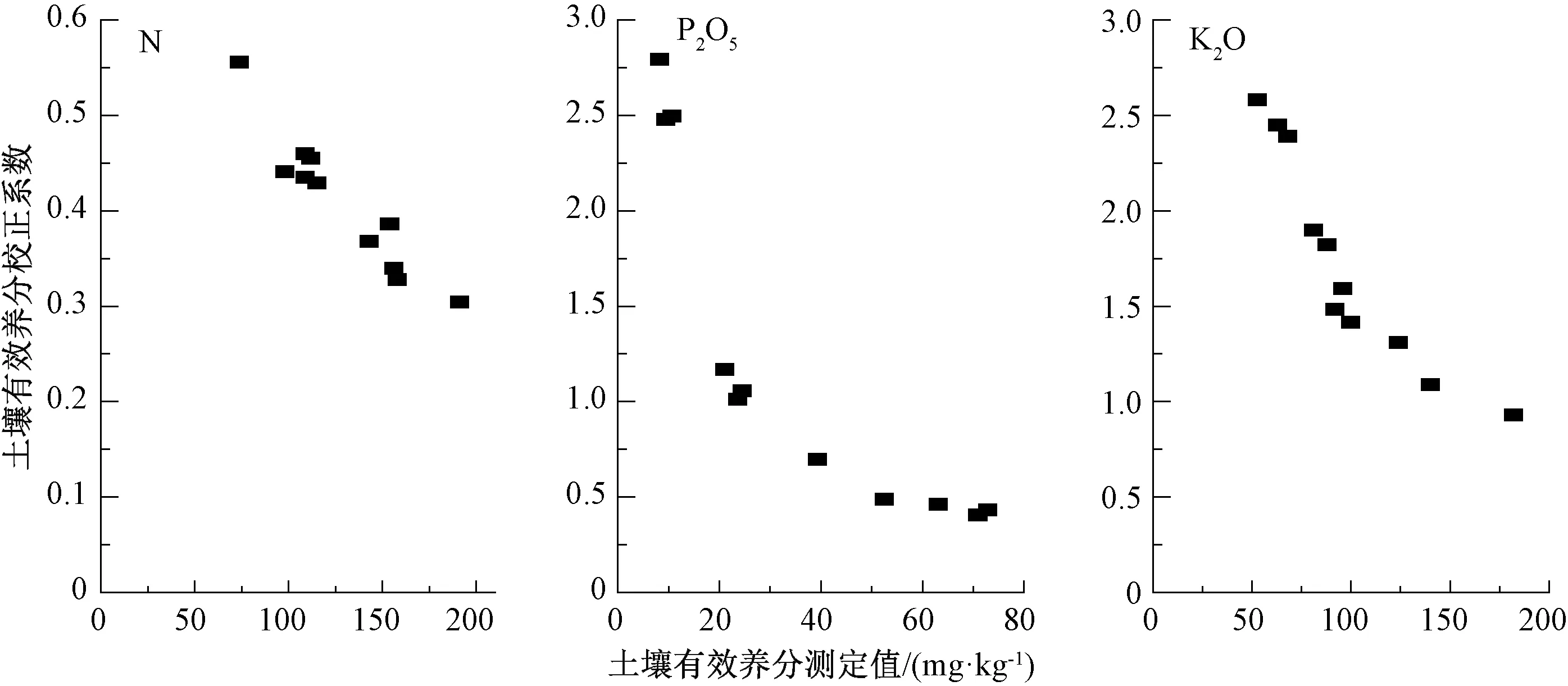
图1 土壤有效养分测定值与土壤有效养分校正系数的关系

图1显示，土壤有效养分校正系数均随其测定值的升高而降低。土壤碱解氮、有效磷、有效钾测定值分别为74～191、8.3～72.9和53～182 mg·kg-1，对应的土壤有效养分矫正系数分别为0.556～0.304、2.795～0.404和2.582～0.931。

土壤有效养分测定值(X)与其校正系数(Y)的回归关系曲线见表1。总体而言，对数函数、双曲线函数和幂函数3种模型形式均具有很高的拟合度(R2>0.920 0,P<0.01)，均可用于估算土壤有效养分矫正系数。

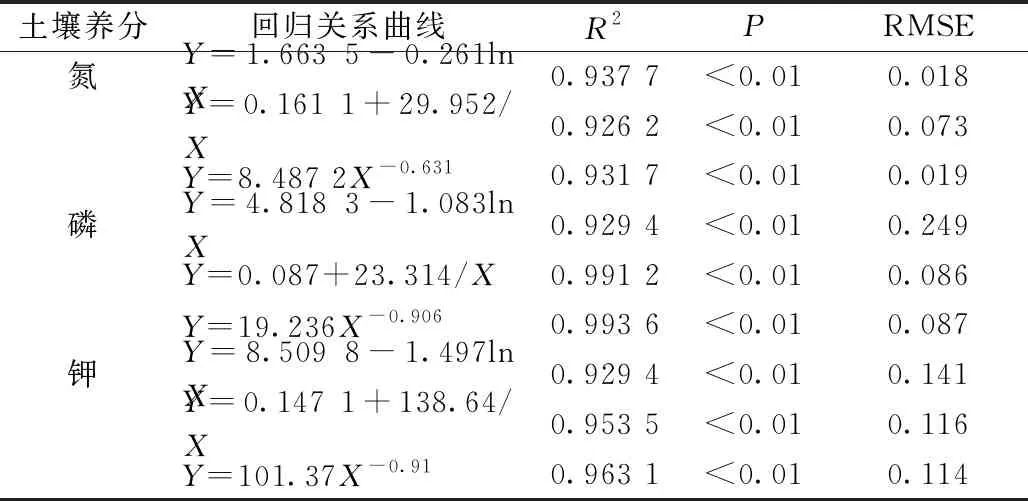
表1 土壤有效养分测定值(X)与其校正系数(Y)的回归关系曲线

就碱解氮而言，3种回归关系曲线的R2分别为0.937 7、0.926 2和0.931 7，RSME分别为0.018、0.073和0.019。对数模型的R2最大、RMSE最小，因此，相对而言，对数模型的拟合度较高。

就土壤有效磷测定值与其矫正系数回归曲线而言，对数模型的R2小于双曲线模型与幂函数模型，RSME大于双曲线模型与幂函数模型。但双曲线模型的R2与RSME和幂函数模型的R2与RSME非常接近，故两者的拟合度相当。

土壤有效钾回归关系曲线的3种形式中，幂函数模型的R2最高、RMSE最小，因此，相对而言，幂函数模型对土壤有效钾与其校正系数回归曲线的拟合度最高。

2.2 土壤有效养分测定值与土壤养分供应量估算值的关系

土壤氮、磷、钾测定值(X)与土壤养分供应量估算值(Y)的关系见图2～4。采用校正系数对数模型与土壤有效养分测定值乘积作为土壤养分供应量估算值时，其与土壤有效养分测定值的回归关系曲线为二次抛物线模型，且二次项系数<0(图2中A、图3中A、图4中A)。模型表达式分别为Y=-0.001X2+0.409X+15.771(R2=0.999 3)、Y=-0.016X2+1.134X+13.851(R2=0.979 7)、Y=-0.007X2+1.549X+74.908(R2=0.989 7)。因此，由此模型计算的土壤养分供应量估算值随土壤有效养分测定值的增加呈先升高后降低的趋势，估算值存在一个最大值。

采用校正系数双曲线模型与土壤有效养分测定值乘积作为土壤养分供应量估算值时，其与土壤有效养分测定值的回归关系曲线为直线模型(图2中B、图3中B、图4中B)。模型表达式分别为Y=0.161 1X+21.952(R2=1)、Y=0.087X+23.314 (R2=1)、Y=0.147X+138.64(R2=1)。因此，土壤养分供应量估算值随土壤有效养分测定值的增加而增加。

采用校正系数幂函数模型与土壤有效养分测定值乘积作为土壤养分供应量估算值时，其与土壤有效养分测定值的回归关系曲线为幂函数模型(图2中C、图3中C、图4中C)。模型表达式分别为Y=8.487 2X0.369(R2=1)、Y=19.236X0.094(R2=1)、Y=101.37X0.09(R2=1)。理论上，土壤养分供应量估算值随土壤有效养分测定值的增加而趋近一个最高值。

A—校正系数对数模型与土壤有效养分测定值乘积；B—校正系数双曲线模型与土壤有效养分测定值乘积；C—校正系数幂函数模型与土壤有效养分测定值乘积。图3～4同。

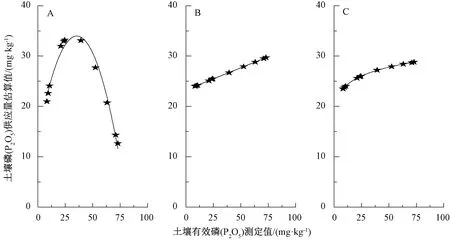
图3 土壤有效磷测定值与土壤磷供应量估算值的关系

图4 土壤有效钾测定值与土壤钾供应量估算值的关系

3 小结与讨论

土壤有效养分校正系数随土壤有效养分测定值的升高而降低，两者的回归关系曲线可拟合为对数模型、双曲线模型和幂函数模型。根据回归曲线函数的R2和RSME可以判断模型的拟合度和准确性。R2越大、RMSE越小，回归曲线的拟合度越高、准确性越好，这为回归关系曲线的选择提供了统计学标准。

土壤有效养分测定值与其校正系数间存在显著的对数曲线关系。这与韩银生等[12,9,17]的研究结论相一致。由此进一步估算的土壤养分供应量估算值随土壤有效养分测定值的增加呈先升高、后降低的趋势，两者间为显著的二次抛物线型曲线关系。不施肥时的土壤养分供应量等于作物养分吸收量。因此，不施肥时作物养分吸收量与土壤有效养分测定值(类似于土壤养分数量)间为二次抛物线关系。在作物施肥效应试验中，如采用二次抛物线模型拟合肥效函数[21-22]，则作物养分吸收量与肥料养分施用量关系曲线与此相类似。

土壤有效养分测定值与其校正系数间存在显著的双曲线关系，这与陈小虎等[10,23]的研究结果相似。由此估算的土壤养分供应量与土壤有效养分测定值间呈显著的线性关系，即土壤养分供应量随土壤有效养分测定值的增加而增加。如果作物产量与肥料养分施用量关系曲线为线性方程[24]，则其推算的作物养分吸收量随肥料养分施用量的变化规律与此相类似。而且，该线性方程的斜率值很小，因此，在较小幅度的土壤养分测定值区间内，土壤养分供应量估算值较为接近，可以取一个近似结果。据此可把土壤养分数量分成几个分段，每个分段的土壤养分供应量分别为一个固定值。例如，刘成祥等[7]将土壤有效磷(Olsen-P)分为“高” “中”“低”“极低”4个分段，对应的土壤有效养分测定值分别为>14、14～>4、4～>1、1～0 mg·kg-1，对应的土壤磷(P2O5)供应量分别为207.3、190.8、162.0和135.0 kg·hm-2。

土壤有效养分测定值与其校正系数间存在显著的负相关型幂函数关系。由此估算的土壤养分供应量与土壤有效养分测定值间仍呈显著的正相关型幂函数关系，即土壤养分供应量估算值随土壤有效养分测定值的升高而升高并接近一个极限值。在肥料养分施用量与作物产量关系试验中，若以抛物线+平台[25]或线性+平台模型拟合肥料效应函数方程[26]，则其养分吸收量估算值随肥料养分施用量变化规律与此相似。

3种养分校正系数拟合方程估算的基础产量作物养分吸收量与土壤有效养分测定值间的回归关系曲线呈现3种函数模型，分别对应3种肥料效应函数作物养分吸收量估算值与肥料养分施用量回归关系曲线。这说明，土壤有效养分校正系数与肥料利用率相类似[27]。而基础产量作物养分吸收量由基础产量与养分系数相乘获得[28]。因此，基础产量养分吸收量与土壤有效养分测定值回归关系实际反映基础产量与土壤养分数量的关系。进而，土壤有效养分校正系数回归关系曲线实际反映的是基础产量与土壤有效养分测定值间的相互变化关系。这为土壤有效养分测定值与其校正系数回归关系曲线的选择提供了实践应用标准。