恒定轮距的多连杆式独立悬挂系统设计

李荣华 杨景山 郑宇锋 周 唯

1.大连交通大学机械工程学院，大连，116028 2.中国人民解放军91550部队，大连，116023

0 引言

机器人机动性对跟踪目标很重要[1]。现有的麦克纳姆(Mecanum)轮式全方位移动机器人越障行驶时，传统悬挂系统形变产生的轮距变化和轮毂中心面侧倾会导致轮子着地性差、辊子表面磨损严重、运动控制难度增加等问题[2-3]，因此，研究先进的机器人悬挂系统成为近年来诸多学者的目标[4-6]。杨霖[7]设计了一种可同时减小路面对车体的垂向力和轴向力的独立悬挂装置，但采用该装置的机器人在越障行驶时，轮子安装支座绕悬挂装置与本体的连接轴旋转导致轮距变化和轮子侧倾。郑仁辉[8]设计的三角形结构的弹簧液压阻尼悬挂装置能保证轮子在越障过程中不产生倾斜，但车轮被障碍物抬起时，连杆绕与车身铰接的轴旋转，导致轴距发生变化，影响机器人的运动精度。丁聪[9]设计的双横臂式平行四边形独立悬挂装置可保证车轮与车体始终垂直，但机器人越障行驶时的轮距会发生变化。张淇杰等[10]设计的一种单自由度多连杆机构弥补了烛式悬架的不足，但连杆与主销的铰接点和轮子中心有一定的距离，在底盘与载重物的重力作用下，悬挂装置在越障行驶过程中对主销的侧向压力较大，使得主销与直线轴承之间产生挤压摩擦；另一方面，不平整路面对轮子的冲击较大时，轮子将出现侧倾，导致轮距改变并增加麦克纳姆轮辊子的磨损。张淇杰等[10]在电机尾部与车架之间增加1根拉力弹簧来减小地面冲击对悬挂装置主销产生的横向力矩，但越障行驶时轮子的上下运动使弹簧拉力产生不规律变化，导致力矩不能被消除。

综上所述，机器人的传统独立悬挂装置在越障行驶过程中能减小地面对车体的冲击力，但不能保证车轮与车体始终垂直、轮距和轴距恒定，导致轮子着地性减弱、轮子与地面产生打滑，增加轮子工作面磨损，影响移动机器人的运动平稳性和操控性能，进而影响行驶精度。因此，亟需设计一款既能保持轮距与轴距恒定不变，又能防止车轮倾斜的新型独立悬挂装置。本文提出一种采用偏置曲柄滑块机构和平行四边形多连杆结构的悬挂装置，并分析其抗路面冲击性能，以解决前述诸多问题。

1 轮式移动机器人本体与悬挂装置的结构设计

轮式移动机器人硬件包括机器人本体、悬挂装置、驱动轮、动力装置和控制器，其中，悬挂装置的选型在机器人越障性能的研究中起主要作用，是本文的核心内容；机器人本体、驱动轮、动力装置和控制器等附属部件，本文只做简要介绍。

1.1 轮式移动机器人本体

机器人本体是所有控制、驱动、传感部件和载重物的载体，是决定整个机器人大概形貌和悬挂装置等各部件设计依据的主要结构。为使机器人轻量化、易装配、便于改型，并保证强度、刚度等各项性能要求，车架主要材料采用1515铝型材。型材4个侧面均有滑槽，便于安装各类配件。组装式车体结构具有改型方便、易于调整各部件位置的优点。车体下部安装的独立悬挂装置与驱动轮和动力系统连接。全向移动机器人的4个麦克纳姆轮的布局与四轮汽车相似。一般情况下，轮距和轴距大致相等，每个麦克纳姆轮配置1台电机(由安装在车体上的控制器和供电系统控制)单独驱动。最终的机器人如图1所示。

图1 四麦克纳姆轮式全向移动机器人Fig.1 4 Mecanum wheeled omni-directional robot

1.2 恒定轮距的独立悬挂装置设计

悬挂装置的承载对象是机器人本体及载重物，一般采用独立悬挂结构[11]。传统的悬挂结构如图2所示，图中，α为侧倾角，d为轮子中心横向偏移的距离。

图2 传统悬挂装置的结构图Fig.2 Schematic of existed independent suspension unit

机器人通过不平路面时，传统结构的悬挂装置使轮子发生侧倾，轮距同时发生变化。不确定的角度变化和轮距偏差影响机器人运动的精度，增加了控制难度和控制算法的复杂程度。

为解决轮距变化和车轮侧倾问题，结合前述独立悬挂装置的优缺点，采用偏置曲柄滑块机构与平行四边形连杆相配合的方法，设计一款可保持恒定轮距的独立悬挂装置。如图3所示，平行四边形结构的一边固接在车架上，与之相对的另一边固接在驱动装置的水平支撑板上。运动过程中，平行四边形的对边始终平行，支撑板与轮子跳动方向始终垂直，可有效解决轮子侧倾的问题。曲柄滑块中，主销的下部与驱动装置支撑架由螺钉固定连接；主销上部与车架上的直线轴承组成滑块机构，限制车轮左右方向的自由度，保证轮距不发生变化。

(a)主视图

(b)俯视图图3 悬挂装置结构图Fig.3 Schematic of suspension unit

弹簧1与主销同轴安装于车架和驱动装置之间。弹簧2和阻尼器连接平行四边形机构右侧的铰接点和车架。弹簧与阻尼器的组合结构可吸收地面对轮子竖直方向的激励力，并将该外力向水平方向分解，减小底盘竖直方向的振动和主销所受的力矩。

图4为机器人经过起伏路面时的悬挂装置图，其中，AD=MF=L1且AD∥MF，点B、C、E、G水平共线，CE=DF=AM且CE∥DF∥AM，CD=EF=L2且CD∥EF。

图4 轮子越障示意图Fig.4 Sketch of robot running over fluctuation road

文中的悬挂装置结构参数及各连杆符号见表1。

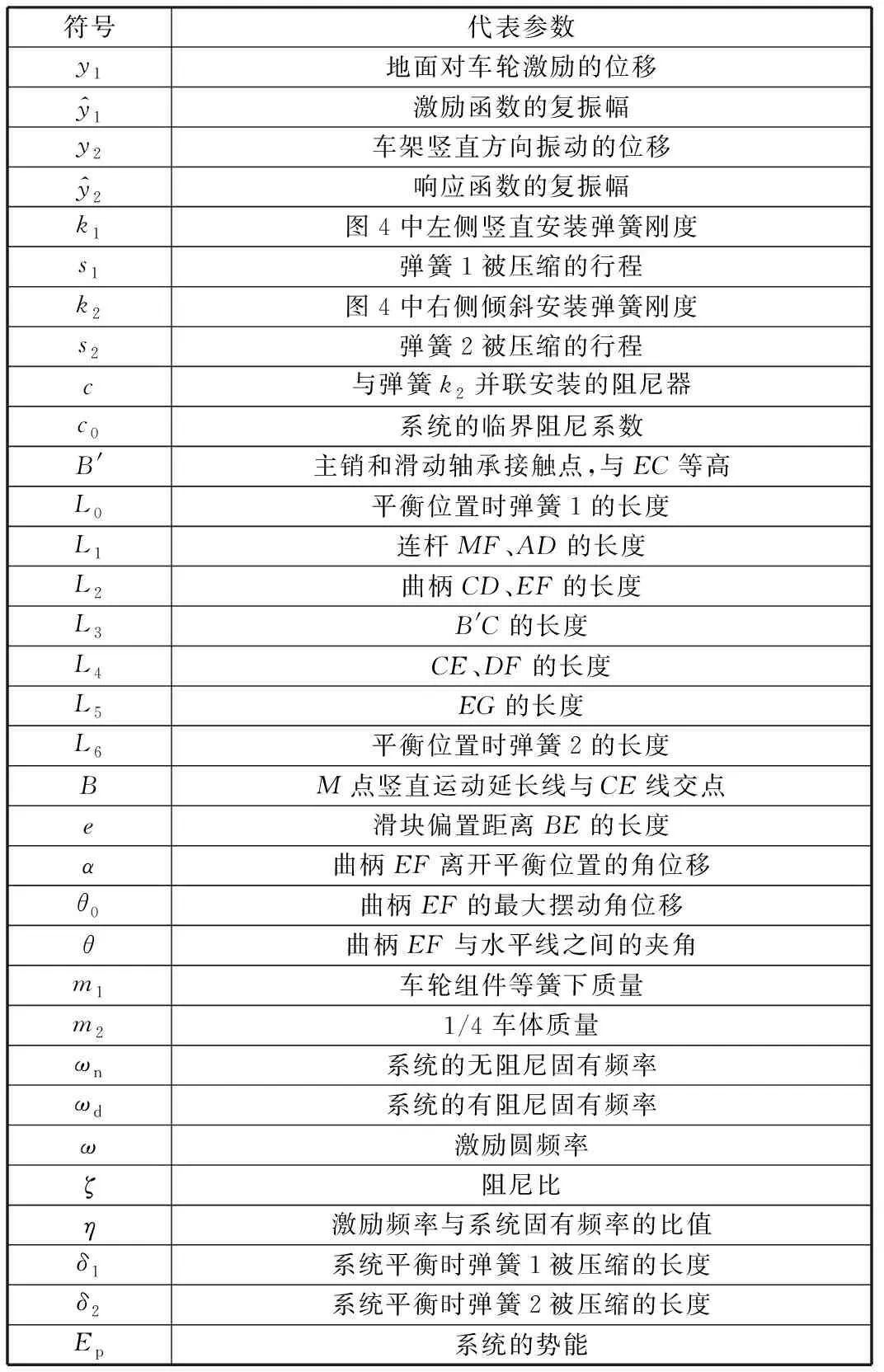
表1 符号参数列表Tab.1 Codes for parameters

2 理论分析

2.1 悬挂系统运动学分析

2.1.1悬挂装置减振位移分析

连杆CD、DF和AD的作用只是加强机构强度，属于虚约束，分析机构运动规律时将其去掉不影响结构运动学分析的正确性。实际设计制造中，连杆CD、AD、DF、EF、FM与机器人本体和车轮安装架组成平行四边形机构，各平行连杆受力相等。与不安装连杆CD、DF和AD相比，安装构成虚约束的3根连杆后，悬挂系统强度增加一倍，因此实际制造中不可省去。图5所示为简化的悬挂装置。设机器人在水平路面静止或平稳运动时，悬挂系统处于平衡位置。以机器人处于平衡位置时的轮毂中心点为坐标原点，水平向右为X轴正方向，Y轴与主销重合，向上为正方向，建立直角坐标系OXY。

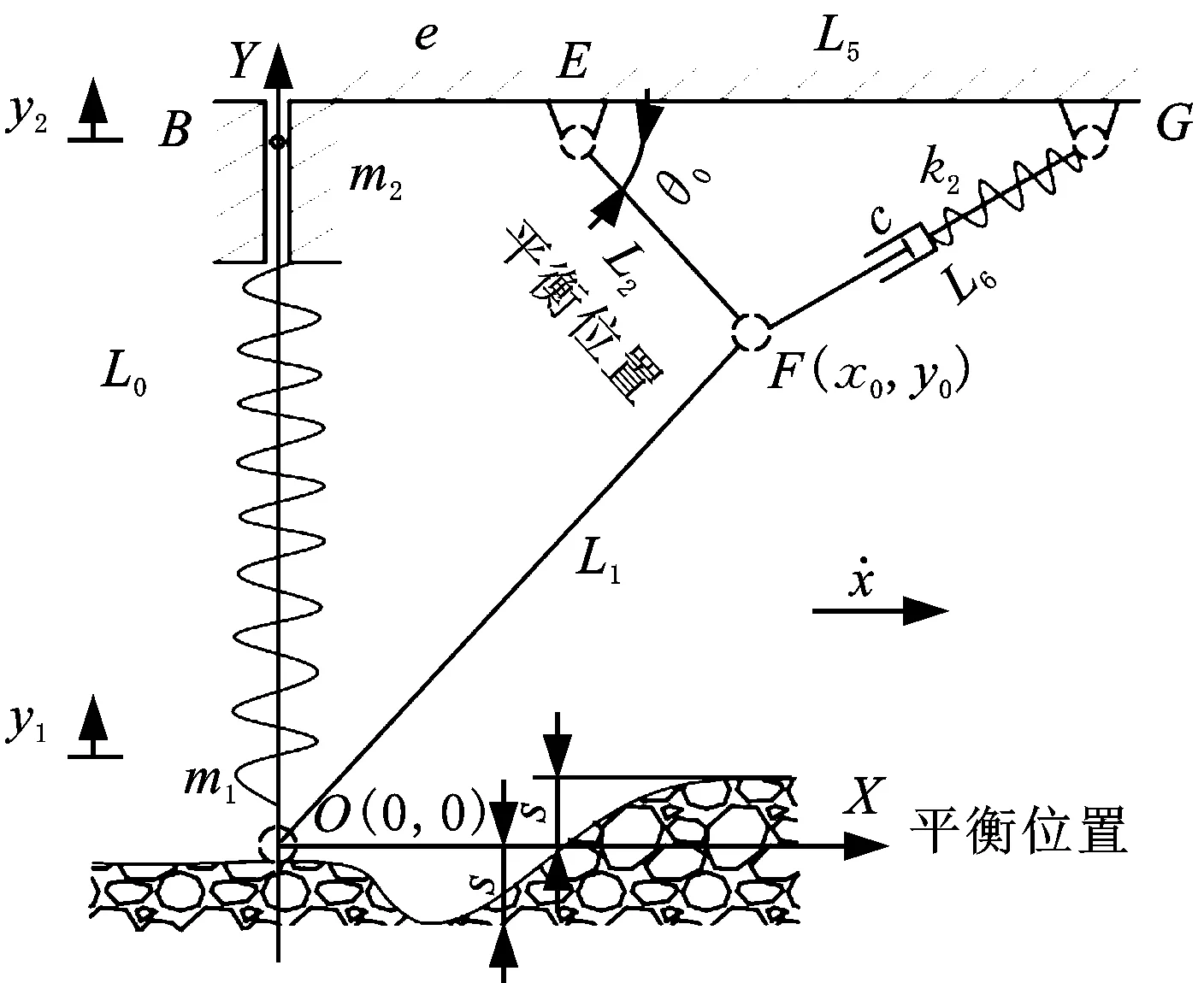
图5 悬挂系统平衡位置简图Fig.5 Sketch of suspension system at equilibrium position

设机器人向右行驶，连杆、弹簧、阻尼器的质量不计。B点为铰接点G、E连线的延长线与Y轴的交点。减振行驶过程中，MB与主销、弹簧1的中心共线，且M点的运动方向始终垂直于机器人本体。弹簧2与阻尼器绕G点转动时，FG的长度随连杆MF、EF的运动而变化。弹簧1与弹簧2被压缩至最短长度时θ=0，其中，θ为连杆EF与水平线之间的夹角。EF顺时针转动至与MF共线(EF与水平线夹角为2θ0)时，弹簧1与弹簧2的伸长量达到最大值。θ=θ0时，系统处于平衡位置，如图5所示。经过运动学分析可得上述多连杆机构的自由度为1。

EF偏离平衡位置的角位移α=θ0-θ。机器人轮子受地面垂直力的作用，产生位移s1。假设车轮始终不离开地面，则弹簧1的变形量也为s1，MB的距离变为L0-s1或L0+s1。同时，弹簧2的压缩量(或伸长量)为s2时，FG的长度为L6-s2(或L6+s2)。弹簧1上M点的振幅为A1，弹簧2上F点在FG方向上的振幅为A2。减振行驶过程中，MF做平面运动。设系统处于任意位置时F点的坐标为(x，y)，平衡位置时的坐标为(x0，y0)。为使悬挂系统有效工作，振动过程中，F点需始终处于M、G连线的上方且连杆EF只能在M、E、G三点所围的三角形内部摆动。

系统处于平衡位置时，连杆的几何关系如下：

(1)

x0=e+L2cosθ0

(2)

y0=L0-L2sinθ0

(3)

(4)

轮心M处于最低点时，弹簧1的长度L0、曲柄偏置距离e、连杆MF、EF的几何关系如下：

(L0-s1)2+e2=(L1+L2)2

(5)

由式(1)～式(5)可得

(6)

图6所示为车轮在路面最低点(弹簧伸长量最大)的悬挂系统振动位移，图7所示为车轮在路面最高点(弹簧压缩量最大)的悬挂系统，图8所示为任意位置的系统。

图6 弹簧伸长量最大时悬挂系统振动位移Fig.6 Sketch of suspension system at maximum elongation of spring

图7 弹簧压缩量最大时悬挂系统振动位移Fig.7 Sketch of suspension system at maximum compression of spring

图8 悬挂系统振动任意位置示意图Fig.8 Sketch of suspension system at normal position

图6中，连杆EF长度为L2，EG长度为L5，FG长度为L6，弹簧2的伸长量为s2，结合式(5)可推得

(7)

继而得到

(8)

由式(8)推导出弹簧2的伸长量

(9)

机器人行驶至最高点时，弹簧2的压缩量最大，连杆EF与连杆FG共线，如图7所示。此时，弹簧1的压缩量s1和弹簧2的压缩量s2分别为

(10)

s2=L6+L2-L5

(11)

由式(6)、式(10)知，s1由弹簧1原长L0、连杆MF长度L1、连杆EF长度L2和曲柄偏置距离e决定；由式(11)知，s2由连杆长度L2、L5、L6决定。

悬挂装置处于任意位置时θ<θ0，车轮中心(M点)沿Y轴上下振动，位移为s1。弹簧2相对于其平衡位置振动，位移为s2。各连杆MF、EF、FG、EG、弹簧1长度L0和曲柄偏置距离e的几何关系如图8所示。

图8中，F点为MF、EF与FG的动态连接点，分析F点坐标的变化可得出连杆MF、EF与FG的运动规律，设F点的坐标为

(x，y)=(e+L2cosθ，L0-s1-L2sinθ)

(12)

θ=θ0-α

(13)

(14)

由图8所示的几何关系可得

(15)

因此可得弹簧1的振动位移

(16)

由图8中△EFG连杆与θ之间的关系，得

(17)

由式(17)可得弹簧2的振动位移

(18)

将式(14)代入式(18)，得

(19)

式(19)表明，s1是s2的函数。

各连杆和曲柄除满足上述几何关系外，为使减振装置有效运行，铰接点F应始终位于M、G连线之上，即连杆MF的斜率始终大于FG的斜率：

(20)

式(20)中，L0、s1、s2由机器人初始设计确定，参数L1、L2、θ、e由式(1)、式(5)、式(17)求取。由式(17)、式(18)可知，s1、s2都是θ的单值函数，因此，当各连杆的长度确定之后，各连杆所处的位置可由θ唯一确定。

2.1.2悬挂装置减振速度分析

悬挂装置减振器振动位移s1=y2-y1，s2由θ决定，是时间的函数。因此，将式(16)、式(18)分别对时间t求导数，可得弹簧1与弹簧2的振动速度：

(21)

(22)

2.2 悬挂系统动力学分析

轮式移动机器人的动力特性对运动平稳性和操控性尤为重要[12-13]。设机器人轮子在t时刻受地面激励力作用而升起的位移为y1，经悬挂装置缓冲后，车架位移为y2，弹簧1的压缩行程s1=y1-y2，弹簧2的压缩行程为s2。设2个弹簧的等效刚度为k，阻尼系数为c。

(23)

(24)

由保守系统的能量守恒可得

(25)

具体设计某种规格的机器人时，代入各连杆长度即可求出弹簧的等效刚度k。

通常的激励函数为

y1=S1sinωt=S1ejωt

式中，S1为激励振幅；ω为激励圆频率。

由汽车动力学知识可知机器人受激励时的系统线性微分方程为

(26)

系统的无阻尼固定频率为

系统的临界阻尼系数为

阻尼比为

本文研究弱阻尼系统，设计阻尼比ζ<1。根据机械振动知识，得出有阻尼固有频率

(27)

设激励频率与系统固有频率的比值为

则有

(28)

又因为

因此，式(26)的稳态响应为

(29)

变换式(28)，可求出系统输出和输入振动幅值比：

(30)

由式(29)、式(30)可知，Y2/s2、φ是自变量ζ、η的函数。

3 实验与分析

3.1 ADAMS虚拟样机的运动学与动力学仿真

对于本文研究的移动机器人系统，多体动力学软件ADAMS可满足运动学和动力学仿真分析需求[14-15]。虚拟样机的最大越障高度S=15 mm，悬挂系统处于平衡位置时L0=124.5 mm。全向轮外径为152.4 mm，每个轮子有16根外围辊子，辊子与轮毂中心的偏置角为45°。整车自重约16 kg。车体长度为652 mm，宽度为594 mm。根据式(1)～式(4)和式(20)确定悬挂装置连杆和曲柄的初始长度，并使各项参数满足悬挂装置稳定运行的要求。采用Creo三维制图软件完成机器人整体模型的设计，然后将各构件导入ADAMS，组装机器人的虚拟模型，并添加相应运动副、设置添加麦克纳姆轮与地面的接触力参数等。

搭载传统悬挂装置的轮式移动机器人如图9所示。首先分析相同工况下传统悬挂装置的减振效果，将机器人三维模型导入ADAMS，设置悬挂参数和激励条件，得出机器人本体振幅，如图10所示，红色波动曲线表示机器人无任何减振装置时的振动规律，其振幅约为6 mm，蓝色波动曲线表示机器人搭载传统悬挂装置时的振动规律，其振幅约为2.5 mm，机器人本体的振幅衰减约60%。

图9 加装传统悬挂装置的移动机器人模型Fig.9 Robot equipped with traditional suspension

图10 机器人本体振动曲线Fig.10 Curve of vibration magnitude of robot chassis

设计恒定轮距的独立悬挂装置，优化各参数，使运动变化过程中两弹簧的振幅差保持实时最小，以保证受力均匀。寻找最佳参数使本体振幅y2最小为目标，优化各连杆长度和安装位置。初始设计时，各连杆长度及相关角度和位移按如下参数选取：曲柄偏置距离e=20 mm，弹簧1原长L0=124.5 mm，弹簧1振幅为15 mm，连杆MF长度L1=115.9 mm，连杆EF长度L2=30 mm，连杆EF与水平面的夹角2θ0=1.7 rad，连杆EG长度L5=80 mm，弹簧2及两侧滑动杆组成可伸缩的连杆FG，其长度L6=70 mm，弹簧2的振幅为12 mm。

机器人本体由2个弹簧共同支撑，系统处于静平衡状态时，机器人本体及载重物的总质量为4m2g，每个悬挂装置上的弹簧载重为m2g。弹簧1的弹性支撑力为k1Δs1，弹簧2的弹性支撑力为k2Δs2，其中，Δs1为弹簧1的压缩量，Δs2为弹簧2的压缩量。平衡位置时，弹簧1的长度为s10，弹簧2的原长为s20。由式(19)中弹簧1与弹簧2的振动位移之间的关系，可推出s10+Δs1与s20+Δs2之间有s2与s1之间相同的函数关系：

设弹簧原长时的机器人本体处于零势能点，根据保守力场的性质，平衡位置时的机器人本体重力势能减少量与2个弹簧的弹性势能增加量相等，即有

m2gΔs1=(k1(Δs1)2+k2(Δs2)2)/2

(31)

设θ10、θ20分别为平衡位置时连杆MF和曲柄EF的转角，FL1、FL2分别为连杆MF和曲柄EF上的受力大小。由图8中各连杆几何结构可得连杆间受受力关系：

(32)

弹簧1与弹簧2对机器人本体的共同支撑作用可用有效刚度为k的弹簧来代替，即

(33)

将悬挂装置的承载质量5.7 kg代入式(31)，可计算出有效刚度k=2.5 N/mm，经多次计算与试验，确定设计阻尼系数c为4.5 N·s/m。各连杆长度对机器人本体振幅影响的敏感程度不同，为找出悬挂系统的最佳连杆长度组合，首先采用变量控制法初步选择每个连杆长度的范围，再进行优化设计[11]。滑块偏置距离e决定悬挂装置的整体尺寸，连杆EF的长度L2对弹簧2的振动变形量和横向力的分解程度有影响。另外，在各种可能的连杆长度组合中，选择一组长度使所有连杆长度之和最小，达到轻量化的目的。参考汽车动力学中悬挂装置设计分析方法，取1/4车辆模型对悬挂装置进行分析，并将结果参数反馈回机器人模型，如图11所示。

图11 ADAMS中1/4机器人模型Fig.11 1/4 model for robot in ADAMS

首先探索各连杆长度参数对悬挂装置振动性能影响的灵敏度[16]，仿真实验表明，滑块偏置距离e增大时，机器人本体振动幅度减小，如图12、图13所示。图13示出了ADAMS中其他连杆尺寸不变，以e为变量寻找本体振幅最小值的曲线。

图12 滑块偏置距离e不同取值对本体振幅的影响Fig.12 Vibration magnitude of chassis affected by e

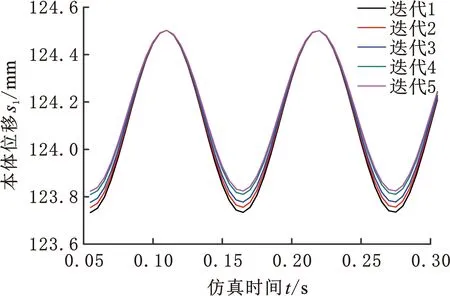
图13 迭代结果曲线图Fig.13 Curves of iteration result

图5中的F点向右移动而其余连杆参数不变时，机器人本体振动幅度有微小增大，这是因为F点右移导致弹簧2受水平方向的分力减小，受竖直方向的分力增大。F点的上下移动对机器人本体振幅的影响不太敏感。图5中，G点右移时L5增大，机器人本体的振幅减小很快；G点左移时，L5减小，机器人本体的振幅增大较快。G点右移时，弹簧2所受外力水平方向的分量减小，竖直方向的分量增大，因此，L5对机器人本体振动幅值的影响敏感度最大。仿真结果如图14所示。

图14 L5对机器人本体振幅的影响Fig.14 Vibration magnitude of chassis affected by L5

最终确定的各连杆最佳尺寸参数如下：曲柄偏置距离e=19.8 mm，连杆MF长度L1=115.9 mm，连杆EF长度L2=30 mm，连杆EG长度L5=87.2 mm，连杆FG长度L6=71.1 mm，连杆EF与水平方向的夹角2θ0=1.7 rad。

按上述各参数重新绘制机器人三维图，将图形导入ADAMS。设置路面障碍高度为15 mm，行驶速度1 m/s，车轮在整个运动过程中不离开路面，因此，机器人轮子竖直方向的位移也为15 mm。为每个电机添加各自的驱动参数，进行越障运动测试。

由图15的仿真曲线来看，机器人底盘振幅降至0.08 mm左右，运行很平稳，轮子振动停止时，车架迅速平稳回到了平衡位置。

图15 优化设计后加装恒定轮距的悬挂装置减振效果Fig.15 Vibration-isolating effect of optimized suspension with constant wheel-track

如图16所示，越障过程中，车轮竖直方向的加速度幅值为1.5×103m/s2，机器人底盘竖直方向的加速度幅值为8 m/s2，车辆运行的平稳性显著增强。

图16 车轮越障加速度与本体加速度衰减曲线Fig.16 Curve of acceleration attenuation of chassis during wheels obstacle surmounting

3.2 实物样机实验与分析

按照仿真结果的优化参数制作的实物样机如图17所示。首先进行机器人平地直线和斜线行驶运动测试，每次测试的行程不小于20 m，速度从0.1 m/s至3 m/s，再进行平地原地旋转和半径5 m的圆周运动测试，测试机器人硬件安装质量和控制系统设置的正确性，然后进行不平整路面的行驶实验。搭载轮距恒定独立悬挂装置的机器人在起伏度不大于30 mm的路面，以0.5～1.0 m/s的速度反复实验，测量机器人运动轨迹与设定轨迹之间的偏差。试验一定次数后，该误差在某个数值范围内的波动不大，则可得出机器人在该设定轨迹的行驶偏差。试验结果发现运动过程中机器人本体平稳，轮子着地性好，减轻了麦克纳姆轮上的辊子与地面之间的打滑。各种轨迹实验所得结果如表2所示。

图17 机器人运动测试Fig.17 Running test for robot

表2 机器人在不同轨迹下的位移误差Tab.2 Displacement errors of robot moving on different trajectories

机器人越过障碍物时，独立悬挂装置保证车轮的振动方向垂直于机器人本体且轮距始终不变，主销所受侧向力小，消除了主销与直线轴承之间的挤压摩擦噪声。

4 结论

(1)分析了可保持恒定轮距的多连杆式独立悬挂装置的结构，建立了悬挂装置各连杆长度之间的几何约束关系和轮子越障运动过程中路面与减振器位移的关系。

(2)ADAMS运动学仿真验证了恒定轮距的多连杆式独立悬挂装置的减振性能。

(3)实物样机试验结果表明，平行四边形与曲柄滑块相结合的多连杆式悬挂装置减轻了麦克纳姆轮辊子与地面之间的打滑，与普通悬挂装置相比，恒定轮距的独立悬挂装置在越障过程中，不会因为悬挂装置的形变而出现轮子侧倾及轮距变化的问题，以及主销受侧向力过大的问题。加装轮距恒定独立悬挂装置的麦克纳姆轮式移动机器人具有良好的越障性能和稳定性，提高了轮子着地性，降低机器人轨迹控制的难度，提高机器人运动精度，增强机动性。

(4)在保持恒定轮距的独立悬挂装置用于其他重载形式移动机器人的研究中，本文只研究了被动悬挂装置，后续研究内容可延伸到主动悬挂装置。