基于Monte-Carlo模拟的小样本下齿轮疲劳极限计算方法及软件开发

李 扬 刘怀举 魏沛堂 毛天雨 陈地发

重庆大学机械传动国家重点实验室，重庆，400044

0 引言

疲劳破坏是重载齿轮的主要失效形式，严重影响装备的寿命及可靠性[1-3]。疲劳强度极限是齿轮等关键零部件设计的重要指标之一，其定义为给定寿命范围内抵抗疲劳失效的最大许用应力，通常通过疲劳试验得到。Dixon-Mood(D-M)法是分析疲劳试验数据并获取疲劳强度极限的常用方法[4-5]。起初，该方法的样本量N大于50的要求通常难以满足[6]，限制了其应用和齿轮疲劳数据建设。LITTLE[7-8]将其推广应用于疲劳极限均值与标准偏差的评估后，研究人员发现获得较准确均值并不需要太多样本，BROWNLEE等[9]发现样本量N缩小至5～10时，D-M法的均值μ也是可靠的。SVENSSON[10]通过分析小样本(N≤30)模拟测试结果发现D-M法的标准差估计值σ有偏。张天飞等[11]通过大量Monte-Carlo模拟发现，D-M法估计的均值μ无偏、σ有偏。SVENSSON等[12]提出了标准差的线性矫正因子(以下称为Svensson-Lorén公式)，并认为该方法可改进包括D-M法在内的所有最大似然评估方法。现行的标准方法[13-15]建议D-M法运用于解释性研究时的样本需求量不小于14，比初版D-M法的样本需求量大大减小。D-M法应用的日益广泛对D-M法本身的误差分析及控制提出了更高要求。MÜLLER等[16]利用4种方法对阶梯试验结果进行分析，发现样本量小于20时，应根据经验或文献对标准差进行估计，而不是采用D-M法计算。ZHAO等[17]采用最大似然原理对疲劳极限的平均值和标准差进行评估，根据试验结果中成对失效越出样本的局部S-N关系，并结合疲劳极限相关物理公式和统计理论推导得出疲劳极限数据。

尽管上述研究对D-M法进行了探索和修正，但仍未能解决小样本情况下估计标准差存在偏差的问题。本文采用Monte-Carlo模拟仿真，基于标准差修正和样本扩充，提出改进疲劳极限标准差估计新方法(Chongqing University bootstrap，CQUboot)[18]，并编写小样本分析软件。该软件对10组不同试件工艺状态和试验参数的D-M法数据的分析验证了CQUboot法的适用性。

1 D-M法与小样本分析方法

1.1 D-M法

疲劳极限可以被理解为具有给定预期疲劳寿命NC的疲劳强度[13]。以齿轮弯曲疲劳极限为例，综合考虑适用性和安全性，NC通常定义为3×106次循环[19]。如图1所示，D-M法[20]测试首先选择初始应力S0和应力阶梯步长d，若试样1在NC之前发生破坏，则认定为失效，并在S0-d的应力水平测试试样2。若试样2未发生破坏则认定为越出，并将试样3的应力水平设为S0+d。重复此过程，直至数据量足够，且最后数据点推算的下一应力水平与初始应力S0相等，以实现升降图闭合，保证整个试验的应力水平都集中在疲劳极限附近。通常以5%左右的齿轮预估疲劳强度为应力阶梯步长d，以50%的材料抗拉强度为初始应力水平S0。

图1 D-M法示意图Fig.1 Schematic diagram of the D-M method

试验完成后进行数据统计处理，将应力水平按升序排列。根据D-M法提供的疲劳极限分布参数估计式，计算应力平均值μ和标准差的估计值σ：

(1)

(2)

式中，i为排序后的应力等级，i= 0，1，2，…；fi为应力等级i下的失效或越出频次。

以失效数计算时，式(1)中取“-”；以越出数计算时，式(1)中取“+”。

1.2 基于标准差修正和样本扩充的小样本分析方法

针对小样本条件下D-M法标准偏差的估计偏差较大等问题，提出了一种基于标准差修正和样本扩充的评估方法(CQUboot法)，提高标准差估计值的准确性，减小统计结果的分散性。

CQUboot法路线如图2所示，阶梯试验应力等级i=3时，采用Svensson-Lorén公式[12]对标准差估计值进行修正：

图2 CQUboot法技术路线图Fig.2 Technical roadmap of CQUboot

(3)

式中，σSL为修正后的估计值；σDM为D-M法的标准差估计值；n为样本量。

文献[21]指出疲劳强度分布的标准差是应力阶梯步长d和估计值σDM的函数。在此基础上，本文充分考虑样本量的影响，构建了修正标准差估计值的函数关系式：

(4)

式中，σCQU为修正后的标准差估计值；C、D、m为随样本量变化的参数，见表1。

表1 不同样本量下的参数值Tab.1 Tab.1 Parameter values of different sample quantity

应力等级i=4时，采用式(4)对标准差进行修正，所得平均估计值更接近真实值，但其统计结果更分散[18]。本文方法在上述标准差修正的基础上，将Monte-Carlo模拟引入基于失效概率的样本扩充。针对每一个试验点，比较试验点应力水平的失效概率与[0，1]区间内的随机数，若随机数小于失效的概率，则判定该点失效，否则为越出。对任意组试验所有样本点重复该过程，生成对应的虚拟阶梯测试数据，以降低标准差的统计分散性，减小标准差估计误差。

应力等级i≥5时，阶梯数量较大，数据更加分散。小步长如d<1.0σ的情况下，结合标准差修正与样本扩充的结果分散程度小；步长d>1.0σ的情况下，结合D-M法与样本扩充的效果较好。

CQUboot法在可靠度R下的疲劳极限为

σlim，R=μlim+σ′Φ-1(1-R)

(5)

式中，μlim为疲劳极限的均值；σ′为优化后的标准差估计值，σ′=σSL，σDM，σCQU；Φ-1(*)为标准正态分布反函数。

2 软件开发

图3 齿轮疲劳极限计算软件逻辑框图Fig.3 Logic diagram of gear fatigue strength calculation software

2.1 基于Monte-Carlo模拟的样本扩充及标准差修正模型的建立

采用Python语言，搭建基于Monte-Carlo模拟的样本扩充及标准差修正计算模型，并对其进行封装(供Qt框架调用)，实现数据流互通。该过程需配置Numpy、Scipy和Matplotlib的相应环境。其中，Numpy对输入分布进行随机抽样，实现Monte-Carlo模拟阶梯试验，并生成均匀分布随机数，进一步与试验中每个应力水平的失效概率对比，实现样本扩充。利用Scipy中的优化器模块求解本文模型中的标准差修正函数等。Matplotlib为本文模型提供多样的可视化输出，通过调用Matplotlib绘制相关图形来表示失效概率数据(F-S数据)、标准差和期望的频率分布等。

一方面，为对比各方法的差异，该模型根据齿轮弯曲疲劳极限已知的真实分布进行多次Monte-Carlo模拟；另一方面，该模型需通过D-M法对试验数据进行分析并实现样本扩充和标准差修正。为实现上述两项功能，将该模型划分为4个模块：Monte-Carlo模拟阶梯试验、D-M法分析、样本扩充、标准差修正，各模块的输入输出如图4所示。

图4 程序功能实现技术路线图Fig.4 Technical roadmap of program functions

2.2 调用样本扩充及标准差修正模型方法

图5 调用模型的技术路线Fig.5 Technical roadmap of calling model

通过上述方法调用封装完成的模型后，再利用Qt平台的windeployqt集成工具将应用软件进行打包发布，使得软件可在未配置任何开发环境的计算机上使用。

2.3 软件功能模块设计

齿轮疲劳极限计算软件由数据库管理、常规数据统计、D-M法分析和小样本分析4个功能模块组成。数据库管理模块具备存储、查询和修改齿轮疲劳试验样本信息的功能。常规数据统计模块统计分析数据库内选取的试验集，完成试验数据的预处理。D-M法分析模块根据阶梯试验得到各应力级下的“越出”和“失效”试验点的分布，选择总点数较少的“越出”或“失效”作为分析事件，计算疲劳极限均值和标准偏差的估计值，求得各可靠度下的疲劳强度极限。小样本分析模块在D-M法计算的均值和标准差基础上，采用CQUboot法进行样本扩充和标准差修正，最后实现误差分析和小样本齿轮疲劳极限计算。相比于D-M法，该模块所需输入样本少且计算更准确。软件主界面如图6所示。

图6 软件平台界面Fig.6 Software platform interface

3 试验验证与分析

为对比D-M法和CQUboot法的分析效果，并测试齿轮疲劳极限计算软件的性能，分析了10组不同工艺、不同加载步长的齿轮弯曲疲劳极限试验数据，验证CQUboot小样本分析方法在齿轮弯曲疲劳极限评估的适用性。

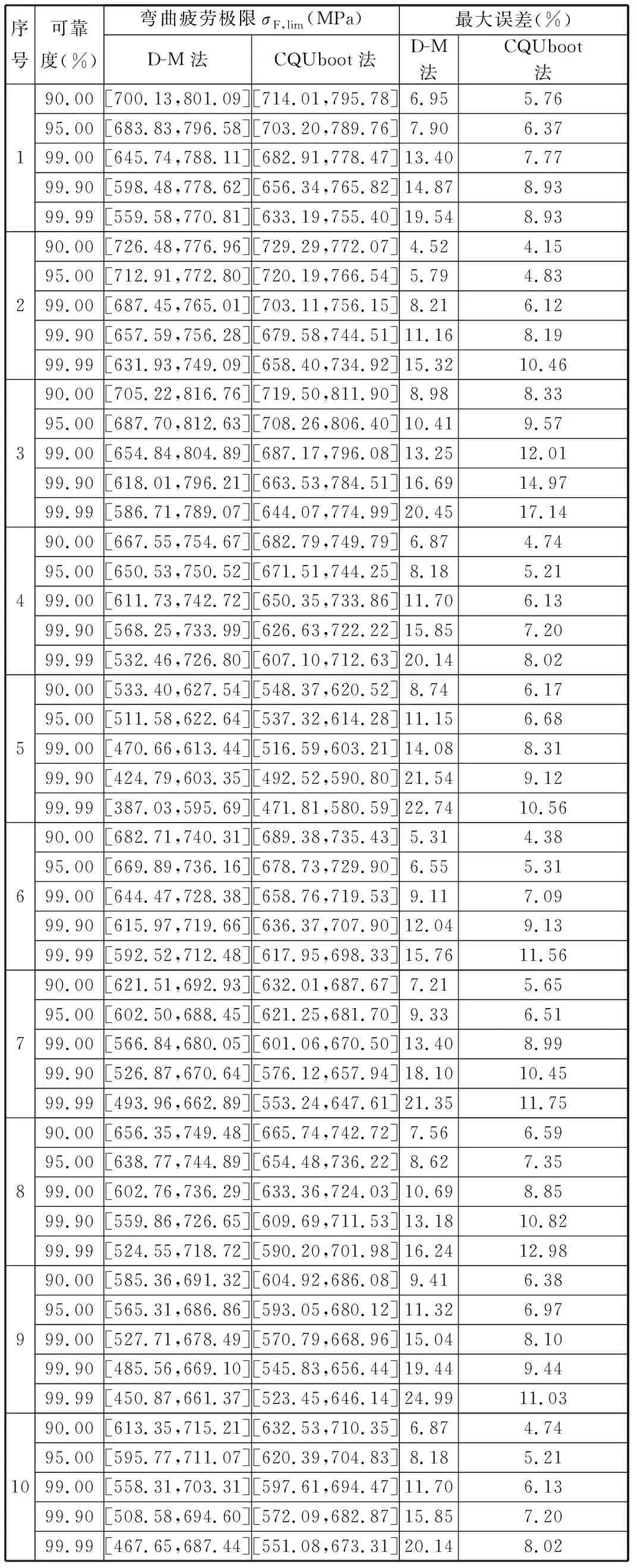
齿轮试件材料为18CrNiMo-7-6，表面均经渗碳淬火处理，基本参数如表2所示。将所有试验数据提前录入数据库管理模块，采用D-M法分析模块计算其中的10组阶梯试验数据，得到各组试验的均值和标准差的估计值，如表3所示，10组数据试验步长范围是0.58σ～1.89σ，满足D-M法对步长与标准偏差比值的要求(0.5σ

表2 试验齿轮基本参数Tab.2 Basic parameters of test gears

表3 D-M法试验结果的参数估计Tab.3 Parameters estimation of D-M test results

针对上述试验，采用与试验相同的阶梯设置，基于Monte-Carlo展开小样本模拟阶梯试验，将表3中的估计值假设为试验的“真实”分布参数输入软件计算模型，分别对每组试验模拟构造12个样本条件下的阶梯试验1000次，其中的1组试验结果如图7所示。模拟结果均存在波动，其中，期望估计值μ为[756.84，820.92]MPa，采用D-M法的标准差估计值σDM为[12.43，61.87]MPa，采用CQUboot法的标准差估计值σCQU为[16.15，39.10]MPa，均值和标准差的波动都将导致各可靠度下的疲劳极限在一定范围内波动。

(a)D-M法均值 (b)D-M法标准差

(c)CQUboot法标准差图7 1000次模拟阶梯试验统计结果Fig.7 Statistical results of 1000 simulated step tests

计算模型考虑期望估计值μ、标准差估计值σDM和σCQU的波动区间，计算不同可靠度下D-M法和CQUboot法的疲劳极限估计区间，得出两种方法相比“真实”疲劳极限的最大误差，具体结果见表4。

表4 12样本量下不同可靠度的疲劳极限预估区间及误差Tab.4 Fatigue strength error of each group test with 12 sample size under different reliabilities with two methods

利用两种方法得到了各组试验样本量下不同可靠度的疲劳极限预估误差，如表4所示，CQUboot法对σFlim的估计值最大误差始终小于D-M法，CQUboot法的最大误差17.14%位于第3组试验的99.99%可靠度下，这是由于该组试验步长0.58σ较小，导致采用CQUboot法估计的误差偏大。其他各组试验在99.99%可靠度下的疲劳极限最大误差为8.02%～12.98%，D-M法的疲劳极限最大误差为15.76%～24.99%。样本减少时，CQUboot法的分析效果好，各可靠度下的疲劳极限更加接近“真实”值。

为进一步说明相同精度下CQUboot方法的样本需求量相比D-M法的减小程度，利用软件中的小样本分析和D-M法分析模块，对上述10组阶梯试验数据开展各小样本量条件下的模拟阶梯试验，每组试验在各样本量条件下均模拟1000次，其中的一组试验数据如图8所示，两方法的标准差估计值均随样本量的增大而减小，但σCQU的区间范围始终小于σDM，σCQU更接近“真实”标准差14.66 MPa。各样本量下期望估计值μ的均值与“真实”期望688.61 MPa几乎一致，但在模拟过程中存在较明显波动，且区间范围随样本量增大而减小，因此，需将期望估计值μ造成的误差考虑在内。

(a)标准差

(b)均值图8 估计标准差和均值的区间分布Fig.8 Interval distribution of estimated standard deviation and mean

针对不同样本量的模拟阶梯试验参数估计区间及疲劳极限误差如图9所示。CQUboot法在所有样本试验下计算所得的齿轮弯曲疲劳极限的误差均小于D-M法。将试验步长从小到大排列会发现试验步长较小的CQUboot法的误差较大，例如试验3、10；误差随样本量的增大而减小的幅度较小，其中，第10组试验样本8下的模拟试验误差最大，为12.66%。试验2和6的步长较大，但误差比其他试验组的小，其中，第2组试验样本18下的误差最小，为5.09%。对比10组数据可知，试验步长d为0.71σ～1.59σ时，CQUboot法比D-M法更优。若以12.66%为允许的最大误差，则D-M法分析需要10～18个样本，CQUboot方法只需8个样本，这充分证明CQUboot法对不同工艺、步长的小样本阶梯试验具有较好效果。

图9 两种方法在不同样本量下疲劳极限的预测误差Fig.9 Prediction errors of fatigue strengthof two methods under different sample sizes

4 结论

(2)将10组不同试件和试验参数的弯曲疲劳数据用于验证本文方法。以D-M法在20～22个样本下计算的99%可靠度的弯曲疲劳极限为基准，样本数降至12时，D-M法的最大误差为15.76%～24.99%，而CQUboot法仅为8.02%～12.98%，因此CQUboot法更适合疲劳极限的小样本统计分析。

(3)CQUboot法试验步长较小时的误差较大，且误差随样本量增大而减小的幅度较小；若以12.66%为疲劳极限预估允许的最大误差，则D-M法至少需要10～18个样本，CQUboot小样本分析方法只需8个样本。