表征干燥失水诱发膨胀土收缩-开裂-沉陷机理的数学模型

张 昭，高帅东，祝良玉，袁昊钰，陈 聪，刘奉银

(西安理工大学 岩土工程研究所，陕西 西安 710048)

1 研究背景

众所周知，膨胀土干燥失水会收缩、吸水会膨胀，其表面在胀缩过程中易发育纵横交错的裂隙，从而在干旱气候条件下显著影响其物理力学性质[1-3]，尤其对水工建筑物的稳定性会产生诸多负面影响。譬如，我国南水北调中线工程输水干渠累计穿越膨胀土段长度约为386.8 km[4]，北疆阿勒泰地区的长距离供水渠道工程总干渠累计穿越膨胀土段约占总长度的32%[5]，这两个典型输水工程中大部分渠段边坡的稳定性问题和劣化模式都与膨胀土发育的裂隙密切相关[6-7]。再如，2007年我国重庆地区遭遇的特大旱情使1200座水库大坝因严重开裂而致使其稳定性降低，直接面临暴雨的威胁[8]。英国、荷兰、美国、澳大利亚等国家境内成百上千米的防洪堤坝长期经受坝体干缩开裂的困扰，每年对坝体内部发育干缩裂隙进行排查和修复的额外经济投入已逾数百亿美元[9]。由此可见，膨胀土因干旱气候引起干缩开裂所诱发的工程地质问题及其灾害在水利工程领域具有相当的普遍性。

由文献[10]可知，膨胀土在干燥失水过程中的孔隙尺寸分布和密度会发生显著变化，在该过程中单个土粒会脱离水合层而使团粒变密实，从而诱发土层开裂和沉陷[11]。唐朝生等[12]和Peng等[13]提出了表征膨胀土中团粒干燥失水收缩的概念模型和数学模型，用以表征其收缩过程经历的4个不同阶段：①结构收缩阶段；②正常收缩阶段；③残余收缩阶段；④零收缩阶段。如何采用土样的收缩曲线预测土层的现场收缩-开裂-沉陷过程值得深入研究。已有学者们采用土层的收缩体积[14-17]及其竖向沉陷[18-19]的现场试验结果来间接描述土层的裂隙特征，但未考虑土层的现场裂隙体积及其尺寸的动态演化过程。值得注意：Coppola等[20-21]在推导膨胀土的双重渗透系数预测模型时，采用团粒区域的收缩特征计算裂隙区域的动态分布。然而，他们的研究未考虑土层的沉陷过程，而且所提出的模型参数针对团粒和裂隙这两个区域是完全不同的，从而限制了其应用范围。

此外，膨胀土的收缩过程与含水率w或基质吸力ψ密切相关[20，22]，而描述孔隙率与含水率关系的参数不能用来描述孔隙率与基质吸力的关系，因此有必要研究膨胀土的收缩特征与基质吸力的关系。

综上所述，为建立干燥失水诱发膨胀土内团粒收缩、土层开裂和沉陷之间的关系，先构建团粒、裂隙和沉陷这三个区域分布的数学模型；再通过分析理想土块与裂隙之间的几何关系，推导裂隙相对宽度的理论计算公式；最后，针对安康膨胀土开展收缩-开裂-沉陷的室内试验，并结合已有文献所述室内和现场试验结果，不仅可验证这三种区域的数学模型在采用同一组参数描述团粒孔隙率、裂隙率及其相对宽度、沉陷率变化过程时的有效性，而且能建立膨胀土团粒孔隙率-含水率-基质吸力的关系。本文提出的数学模型为定量描述膨胀土的体积变化特征和渗透特性提供了一种新方法。

2 数学模型的理论基础与基本假定

依据文献[23]，干燥失水会诱发天然土层产生自其表面向下延伸至一定深度处的裂隙网络，直至土层含水率足够高以阻止其收缩，或上覆荷载足够高以阻止其胀缩，并认为裂隙底部至表面的这部分近地表土层具有“活性”(不考虑上覆荷载的影响)。本文将这部分土层视为若干个土块所构成的典型土层。在构建模型时，不考虑侵蚀及土块运动，且典型土层内的土粒质量m(s)为常数。

典型土层的总孔隙率nmax可由其几何特征确定。膨胀土内的土粒会聚合成若干团粒，而这些团粒会聚合成土粒骨架。若认为土粒内无孔隙，则团粒内形成的孔隙最小，而团粒间孔隙较团粒内孔隙更大、连通性更好。依据文献[24]，在土层的干燥失水过程中，团粒内孔隙的水合层缺失，而团粒间孔隙的基质吸力增大，故团粒内、团粒间的孔径逐渐减小。这里将团粒内、团粒间孔隙体积之和在典型土层体积中所占比例定义为团粒孔隙率n(a)。依据文献[12，25-26]，土层表面会因干缩而产生裂隙，不仅自其表面沿竖向扩展至一定深度处，还会沿水平向贯通扩展。在典型土层中，这种收缩裂隙亦可视为划分各个土块的边界，又称为边界裂隙[27]、棱柱间裂隙[28]或平面裂隙[29]。此外，土层表面的失水收缩也会诱发竖向沉陷，该沉陷区域亦可视为独立于团粒之外的区域。这里将总孔隙率nmax分为团粒孔隙率n(a)、裂隙率n(c)和沉陷率n(s)，如图1所示：当土层含水率较高时，其总孔隙率主要取决于团粒内以及团粒间孔隙构成的团粒孔隙率n(a)；当土层含水率较低时，团粒孔隙率n(a)减小，而裂隙率n(c)和沉陷率n(s)增大。这与Fityus等[30]得出的这三种区域分布随含水率变化会出现相互转化的结论一致。需注意：本文未考虑膨胀土干燥失水收缩和吸水膨胀过程中的滞回特性，在模型推导过程中认为任意含水率的土层均处于热力学平衡状态，不考虑时间对膨胀土胀缩过程的影响。

图1 膨胀土层含水率较高和较低时团粒孔隙率、裂隙率和沉陷率的表征

采用膨胀土的收缩曲线可划分不同含水率w对应的团粒孔隙率n(a)、裂隙率n(c)和沉陷率n(s)所占比例，如图2所示：线段AB、BC、CD分别表示n(s)、n(c)和n(a)；n(a)与w的关系可用最大孔隙率nmax与最小孔隙率nmin间的收缩曲线描述。在干燥失水过程中，n(a)逐渐减小，而n(c)和n(s)逐渐增大(与图1反映的规律一致)。这里将n(c)和n(s)之和称为团粒外孔隙率n(e-a)，表示土层收缩过程中团粒区域外产生的裂隙和沉陷。

图2 采用收缩曲线划分膨胀土的团粒孔隙率、裂隙率和沉陷率

此外，这里在描述膨胀土干燥失水收缩过程中不同孔隙区域所占体积比例与湿度关系时，除采用孔隙率n与含水率w的关系外，亦可通过孔隙率的最大、最小值(nmax和nmin，3.1节详述其定义)和最大含水率wmax进行归一化，可得到归一化的孔隙率N和含水率W的关系：

N=(n-nmin)/(nmax-nmin)

(1)

W=w/wmax

(2)

3 数学模型推导

3.1 团粒孔隙率、沉陷率和裂隙率之间的关系依据第2节的假定，可将膨胀土的总孔隙率分为：

n(t)=n(a)+n(c)+n(s)

(3)

依据文献[31]，将膨胀土样反复胀缩循环后可得到稳定的收缩曲线，这种稳定收缩曲线的最大值nmax与最小值nmin之差称为可逆孔隙率n(rev)，N(rev)为其归一化值：

n(rev)=nmax-nmin=n(a)+n(c)+n(s)-nmin

(4)

N(rev)=N(a)+N(c)+N(s)=1

(5)

式中：nmax等同于n(t)；nmin实质为团粒区域的不可逆孔隙率；N(rev)=(nmax-nmin)/(nmax-nmin)；N(a)为归一化团粒孔隙率，N(a)=(n(a)-nmin)/(nmax-nmin)；N(c)为归一化裂隙率，N(c)=n(c)/(nmax-nmin)；N(s)为归一化沉陷率，N(s)=n(s)/(nmax-nmin)。

3.2 团粒孔隙率的描述已有学者采用三种思路预测膨胀土的收缩曲线：①仅定量描述膨胀土整条收缩曲线中的某一阶段[32]；②假定每个阶段的曲线形状以定量描述整条收缩曲线中的所有阶段[33]；③依据整条收缩曲线的形状推得表达式[34-36]。本文借鉴第③种思路，经过反复试算，得到表征团粒孔隙率与含水率关系的收缩曲线表达式：

N(a)=(1+ξ)Wλ/(1+ξWλ)=(1+ξ)/(ξ+W-λ)

(6)

n(a)=(nmax-nmin)(1+ξ)/(ξ+W-λ)+nmin

(7)

式中ξ和λ为拟合参数。值得注意：式(6)(7)需确定4个参数(ξ、λ、nmax和nmin)，不仅较Groenevelt等[34]和Peng等[35]的模型参数有所减少，而且式(6)(7)的参数可通过收缩试验确定。

3.3 团粒外孔隙率的描述这里将裂隙率和沉陷率之和定义为团粒外孔隙率n(e-a)(N(e-a)为其归一化值)，以描述土层收缩时在团粒以外形成的孔隙。在干燥失水过程中，团粒孔隙率逐渐减小，而团粒外孔隙率逐渐增大，故可将式(6)代入式(5)得到归一化团粒外孔隙率N(e-a)的表达式：

N(e-a)=N(c)+N(s)=1-N(a)=(1-Wλ)/(1+ξWλ)

(8)

此外，可将式(7)代入式(4)得到团粒外孔隙率n(e-a)的表达式：

n(e-a)=(nmax-nmin)(1-Wλ)/(1+ξWλ)

(9)

3.4 沉陷率和裂隙率的描述假定沉陷率与团粒外孔隙率成正比，可得到归一化沉陷率N(s)的表达式：

N(s)=n(s)max(1-Wλ)/[(nmax-nmin)(1+ξWλ)]

(10)

进而根据归一化定义得到沉陷率n(s)的表达式：

n(s)=n(s)max(1-Wλ)/(1+ξWλ)

(11)

式中：n(s)max为W=0时的最大沉陷率，即n(s)max=n(s)(W=0)，可按照如下步骤确定：

(1)依据文献[37-38]，模拟典型土层失水收缩时，可将其简化为若干个形如长方体的理想土块集合体，随着理想土块的收缩，团粒外孔隙率逐渐增大，故可通过这些理想土块的体积变化来描述土层干燥失水引起的收缩-开裂-沉陷过程。由图3(a)(b)所示，本文将典型土层简化为I个形如长方体的理想土块集合体，其中第i个土块的初始尺寸为Li×Li×H(图3(c))，干燥失水收缩后的尺寸为(Li-Bi)×(Li-Bi)×(H-ΔH)(图3(d)，图中：Bi为第i个土块的裂隙宽度，ΔH为沉陷量)。土层的裂隙可视为团粒外区域的非沉陷区域，包括团粒内在任意方向上出现的裂隙以及团粒外的裂隙(即理想土块间的裂隙)。

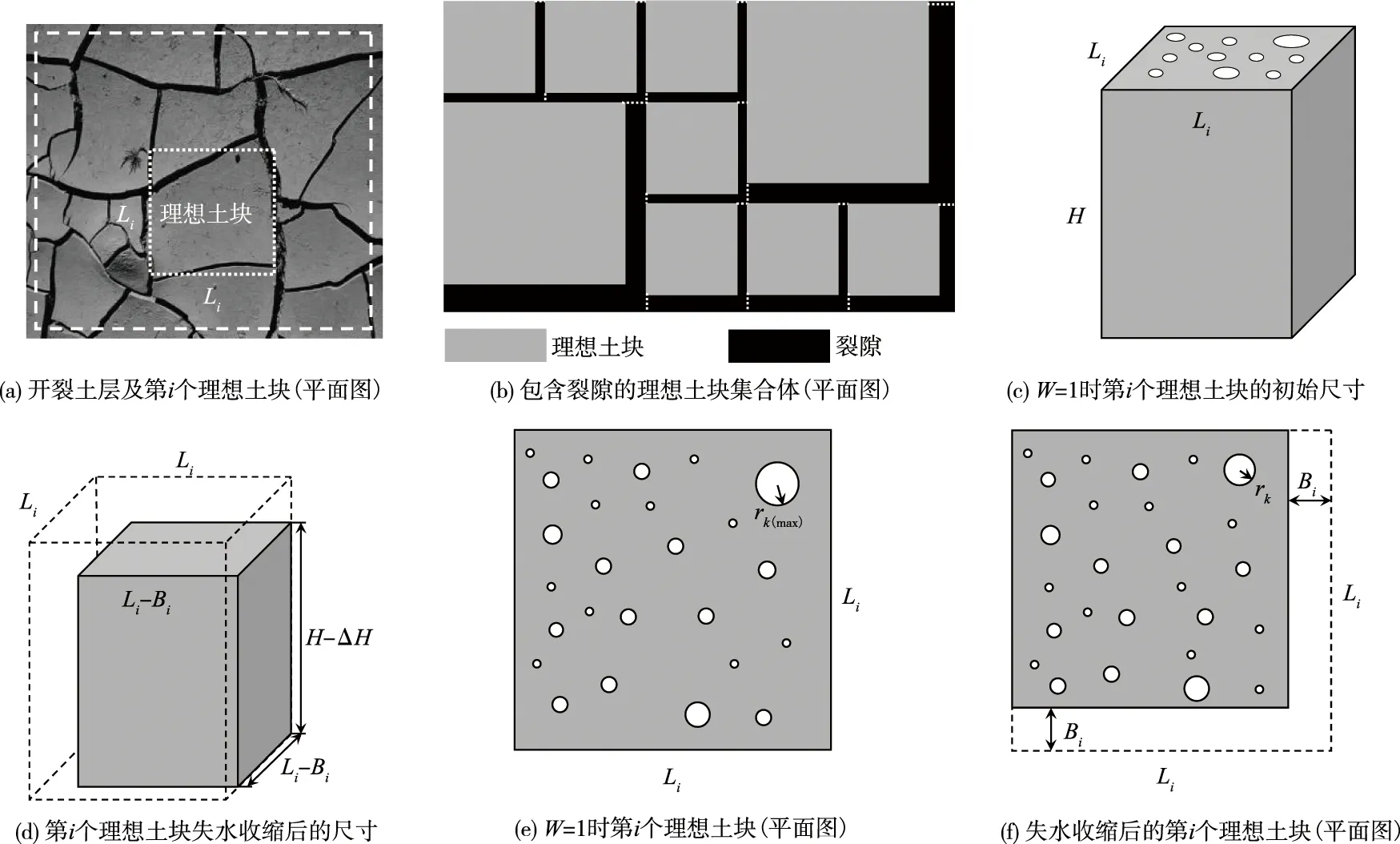
图3 采用包含裂隙的理想土块集合体表征干燥失水诱发膨胀土收缩-开裂-沉陷机理的示意图

(2)引入收缩形状系数χ以表征理想土块体积的相对变化量与其高度的相对变化量之间的关系：

1-ΔV/V(ini)=(1-ΔH/H)χ

(12)

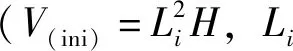
1-ΔV/V(ini)=(Vv(a)+V(p))/V(ini)=n(a)+1-nmax

(13)

式中：Vv(a)为团粒孔隙体积；V(p)为构成团粒的土粒体积。

(3)在图3所示的理想土块集合体中，沉陷率可表示为：

n(s)=V(s)/V(ini)=ΔH/H

(14)

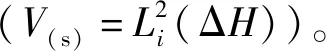
n(s)=1-(1-nmax+n(a))1/ χ

(15)

当W=0时，n(a)(W=0)=nmin，则由式(15)可得n(s)(W=0)的表达式：

n(s)(W=0)=n(s)max=1-(1-nmax+nmin)1/ χ

(16)

式中依据文献[18-19]，若假定土层呈等向收缩，则χ=3。

此外，将式(10)代入式(8)、式(11)代入式(9)，可得到裂隙率的表达式：

N(c)=N(e-a)-N(s)=(nmax-n(s)max-nmin)(1-Wλ)/[(nmax-nmin)(1+ξWλ)]

(17)

n(c)=(nmax-n(s)max-nmin)(1-Wλ)/(1+ξWλ)

(18)

3.5 对土层裂隙相对宽度的预测采用3.2—3.4节推得的团粒孔隙率、沉陷率和裂隙率表达式可预测土层裂隙的相对宽度。如3.4节所述，典型土层干燥失水收缩后第i个理想土块的尺寸为(Li-Bi)×(Li-Bi)×(H-ΔH)(图3(d))。需注意：这里认为当土层的含水率一定时，所有理想土块的高度均相同，即产生相同的沉陷量。

在每个理想土块中，团粒孔隙可用K个圆柱形孔隙描述，其中第k个圆柱形孔隙的半径为rk。当土层在干燥失水过程中，第k个孔隙半径在其最大值rk(max)(图3(e))至最小值rk(min)范围内变化。

需注意：虽然团粒内孔隙的形状不规则、结构迂曲，但由文献[39]可知，对典型片状黏粒构成的团粒间孔隙通常呈管状并能深入土层内部，故本文采用圆柱形孔隙来模拟团粒孔隙。此外，由文献[28]可知，团粒间孔隙的形状一般较为稳定，比团粒内孔隙的收缩量和膨胀量小。因此，下文的推导更关注于形如圆柱的团粒孔隙如何随含水率变化。

在理想土块集合体(图3(a)(b))的失水收缩过程中，当含水率为W时，土块沿竖向产生的沉陷量为ΔH，故其高度变为H-ΔH(图3(d))；由图3(f)可知，当土块失水收缩后，团粒孔隙体积会减小，从而在第i个土块外产生宽度和长度分别为Bi和Li的裂隙。这里假定所有裂隙均形如长方体，即可将图3(f)所示土块右侧和下侧形成的裂隙拼接成尺寸为Bi×(2Li-Bi)×(H-ΔH)的长方体裂隙。

依据图3可先算得含水率为W时，理想土块的团粒孔隙率n(a)：

(19)

式中：Vv(a)为团粒孔隙体积；V(t)为理想土块的总体积(V(t)=V(ini))。需注意：ΔH可由沉陷率算得(ΔH=ΔHmax[(1-Wλ)/(1+ξWλ)]，其中ΔHmax为W=0时的最大沉陷量)。

土层孔隙率的最大、最小值(nmax和nmin)可分别表示为：

(20)

(21)

如3.2节所述，在土层的干燥失水过程中，团粒孔隙尺寸会随含水率变化，故可将式(7)(20)(21)代入式(19)定量描述这两者的关系：

(22)

由于土块的高度远大于沉陷量(即H远大于ΔHmax)，则式(22)可简化为：

(23)

由此可得土层的裂隙率为：

(24)

式中Bi(max)为第i个土块在W=0时的最大裂隙宽度。重新整理式(24)，进而将依据沉陷率求得的ΔH表达式(ΔH=ΔHmax[(1-Wλ)/(1+ξWλ)])代入式(24)中，可得：

(25)

由于2Li远大于Bi(max)，故可将式(25)进一步简化，将裂隙宽度Bi用Bi(max)表示：

(26)

又H远大于ΔHmax，则可将式(26)进一步简化推得I个土块的累计裂隙宽度表达式：

(27)

由式(27)亦可推得第i个土块的裂隙相对宽度表达式：

Bi/Bi(max)=(1-Wλ)/(1+ξWλ)

(28)

由式(27)(28)可知，采用参数ξ和λ(用于计算团粒孔隙率、沉陷率和裂隙率)可计算给定含水率时土块的裂隙相对宽度，亦可通过测定某一含水率的土块对应的裂隙宽度来预测其最大宽度Bmax。需注意：这里认为ξ和λ在宏观尺度不随时空变化，Bmax随空间变化而不随时间变化，含水率w随时空变化。此外，由式(27)(28)亦可知，所有裂隙宽度均成比例变化，使裂隙尺寸保持固定分布，而在低于wmax的含水率范围内变化。总之，当无法确定土层完整的裂隙尺寸分布时，可将Bmax视为有效的宏观尺度参数。

3.6 团粒孔隙率与持水曲线的关系依据文献[22]，膨胀土的收缩-开裂-沉陷过程也与基质吸力ψ有关，故有必要综合分析膨胀土的团粒孔隙率与基质吸力和含水率的关系，为此，可采用van Genuchten模型[40]描述归一化含水率W与基质吸力ψ的关系(即持水曲线)：

W=w/wmax=[1+(αvψ)nv]1/nv-1

(29)

式中：αv为与进气值有关的拟合参数；nv为与减湿率有关的拟合参数。将式(29)代入式(6)(7)，可得到团粒孔隙率(含其归一化值，即N(a)和n(a))与基质吸力ψ的关系：

(30)

(31)

3.7 模型的参数确定采用本文提出的数学模型描述土层中孔隙率的分布时，含水率w是非常重要的变量，此外，还需确定6个参数wmax、nmax、nmin、ξ、λ和n(s)max。其中，前5个参数可采用膨胀土收缩的室内试验结果确定，具体方法如下。

(1)wmax：可在膨胀土的收缩试验前，根据其饱和试样的初始含水率确定；

(2)nmax：可根据nmax=wmaxρs/(ρw+wmaxρs)算得(ρs为土粒密度，ρw为纯蒸馏水的密度)；

(3)nmin：在饱和试样的干燥失水过程中，监测孔隙率随含水率减小而经历文献[12-13]所述的结构收缩阶段、正常收缩阶段和残余收缩阶段，直至含水率减小至缩限以后进入零收缩阶段，进而依据文献[12-13]取零收缩阶段终点对应的孔隙率为nmin；

(4)ξ和λ：将已确定的wmax、nmax和nmin代入式(6)或式(7)，进而用该式对孔隙率关于含水率的收缩实测数据进行非线性最小二乘拟合，从而确定拟合参数ξ和λ(对这两个参数的灵敏度分析详见4.4节)。

此外，n(s)max可通过给定收缩形状系数χ，并将nmax和nmin代入式(16)算得。然而，通过现场试验如何确定这些参数还有待进一步研究。

4 模型的试验验证与讨论

利用已有文献中膨胀土收缩的现场和室内试验、开裂的现场试验以及持水试验结果，并结合安康膨胀土收缩-开裂-沉陷的室内试验，验证第3节提出的数学模型的有效性。

4.1 文献[14，41-42]中膨胀土的收缩-开裂现场试验简介Stewart等[41-42]在两个典型膨胀土试验场开展了膨胀土收缩的现场试验。第一个试验场(规模为2 m×3 m)位于美国俄勒冈州科瓦利斯市附近，属粉砂质壤黏土层，砂粒、粉粒和黏粒含量分别为5%、37%和58%，蒙脱石含量为30%～45%，膨胀性较强；第二个试验场(规模为3.5 m×11 m)位于智利中南部，属壤土层，近地表层(0～20 cm)的砂粒、粉粒和黏粒含量分别为44%、31%和25%，蒙脱石含量为20%～50%，膨胀性属中等。现场试验的分析方法详见文献[41-42]。Stewart等[41-42]在这两个试验场中分别采取3个原状土块试样，采用文献[16]所述图像处理方法分析这些土块试样的胀缩性。

对俄勒冈试验场的土块试样，Stewart等[41-42]将其从田间持水量开始进行收缩试验，并在试验结束后将试样在105 ℃经24 h烘干，以测定试样的最终体积和含水率。在完成收缩试验后，再采用毛细上升作用原理和封闭湿度箱(相对湿度超过99%)对试样进行增湿，以描述其遇水膨胀的性质。此外，对智利试验场的土块试样，Stewart等[41-42]将其先在105 ℃条件下烘干，再放入封闭湿度箱(相对湿度超过99%)增湿，直至试样的含水率趋于稳定后，再将其烘干，通过定期测定试样的体积和质量，描述其在膨胀和收缩过程中的性质。

Navar等[14]在墨西哥西北部的膨胀性黏土层(砂粒、粉粒和黏粒含量分别为20%、30%和50%，黏土矿物为蒙脱石)选取两个试验场(规模为11.3 m×1.3 m)开展收缩-开裂-降雨试验，测得裂隙宽度、积水点、裂隙内的水分流速及其释水量。此外，在两个试验场土层内10、20、30 cm深度处布置张力计，以测定不同时刻的基质吸力，并在降雨试验过程中，对其中一个试验场土层10 cm深度处(基质吸力变化范围最大的深度)在基质吸力为200、120和70 kPa时取样并测定含水率。

4.2 文献[22，43-44]中膨胀土的收缩-开裂-沉陷试验及持水试验简介除4.1节所述膨胀土的现场试验结果外，还可整理文献[22，43-44]的膨胀土收缩试验结果，以对比验证第3节提出数学模型的有效性。Hallaire[43]在深度为120 cm范围的黏土层(黏粒含量为52%～56%，黏土矿物成分主要为蒙脱石和绿泥石)中取得原状试样进行干缩试验，采用位移传感器测定试样的沉陷量，并用直径为0.2 mm的玻璃微珠充填裂隙以定量描述试样的开裂特征，此外，还通过分析土层的现场试验监测数据和图像估算得土层的裂隙体积；Reeve等[44]分别对3种膨胀性黏土样进行收缩和持水试验(测定含水率与基质吸力的关系)，土样编号分别为Wrye Bw、Wrye Bg、Fladbury，相应的黏粒含量分别为58%、64%、59%，粉粒含量分别为35%、31%、26%，黏土矿物成分主要为蒙脱石；Salager等[22]利用压力板仪测定了3个初始孔隙比e0=1.01、0.86、0.68(其中e0=emax)的含黏粉砂样(砂粒、粉粒和黏粒含量分别为72%、18%和10%，液限和塑限分别为25%和14.5%)的体积、含水率和基质吸力之间关系。

4.3 安康膨胀土收缩-开裂-沉陷的室内试验方法除已有文献的试验结果外，本文还对安康膨胀土开展了收缩-开裂-沉陷的室内试验，以进一步验证第3节提出的数学模型。试验所用膨胀土取自陕西省安康市富强机场附近，呈褐黄色，取样深度约7 m。其主要物理力学性质参数如表1所示。至于安康膨胀土的矿物成分，可对其粉末试样开展X射线衍射试验进行鉴定。通过MDI Jade软件分析X射线衍射试验数据以求得衍射强度的特征值和半宽高(如图4所示，其中CPS为每秒收集的光子数，以表征衍射强度，θ为衍射角，蓝色数值为衍射强度特征值对应的半宽高)，进而将这两类数值与JCPDS卡片(包含单相纯净矿物的衍射强度和半宽高)进行比对，最终鉴定出安康膨胀土的主要矿物成分及其含量分别为：伊利石约占45%，蒙脱石约占8.2%，高岭石约占31.5%，石英约占15.3%。

表1 试验用土的主要物理力学性质参数

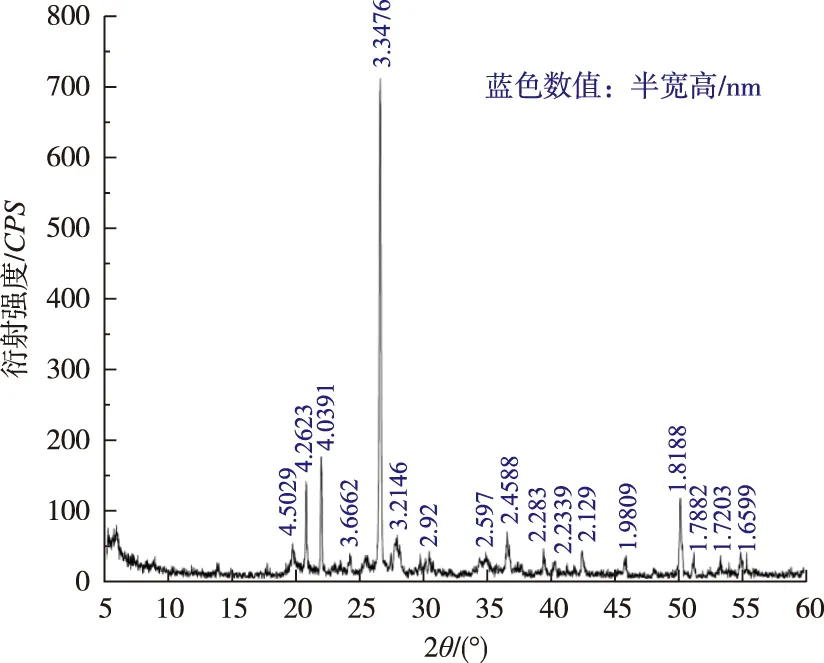
图4 安康膨胀土的X射线衍射图谱

依据文献[45]所述方法开展收缩-开裂-沉陷的室内试验，试验装置主要包括数码相机、支架、遮光板、LED灯(2个，可调节亮度)、电子天平(量程10 kg，精度0.01 g)、计算机(用于图像处理)、长方体试样盒(3个，材质均为透明亚克力板，长、宽、高均分别为160 mm×160 mm×50 mm)，在试样盒四边垂直于其底面中心处设置刻度(长度为0～5 cm、分度值为1 mm)。关于试验步骤，可依据文献[45]，先将取回的土样风干碾碎，过2 mm筛，与适量蒸馏水混合拌匀，配制成初始含水率约为60%的饱和泥浆。再次，称取一定量的泥浆静置于试样盒中，预先在其4个侧面涂抹凡士林，以尽可能消除泥浆样沉陷过程中的挂壁现象，并对其称重。最后，将泥浆样置于室温环境下干燥失水，观测试样的收缩、开裂和沉陷过程。试验中同时放置3个平行试样。在干燥失水过程中，定时称取试样的质量，测定含水率变化，并同时对试样表面和试样盒四边设置刻度处进行拍照，记录裂隙和沉陷的形成和发展过程，进而在MATLAB软件中采用图像二值化处理程序(图5)，并结合Image J软件及其像素比例尺分别计算试样的裂隙率和沉陷率。

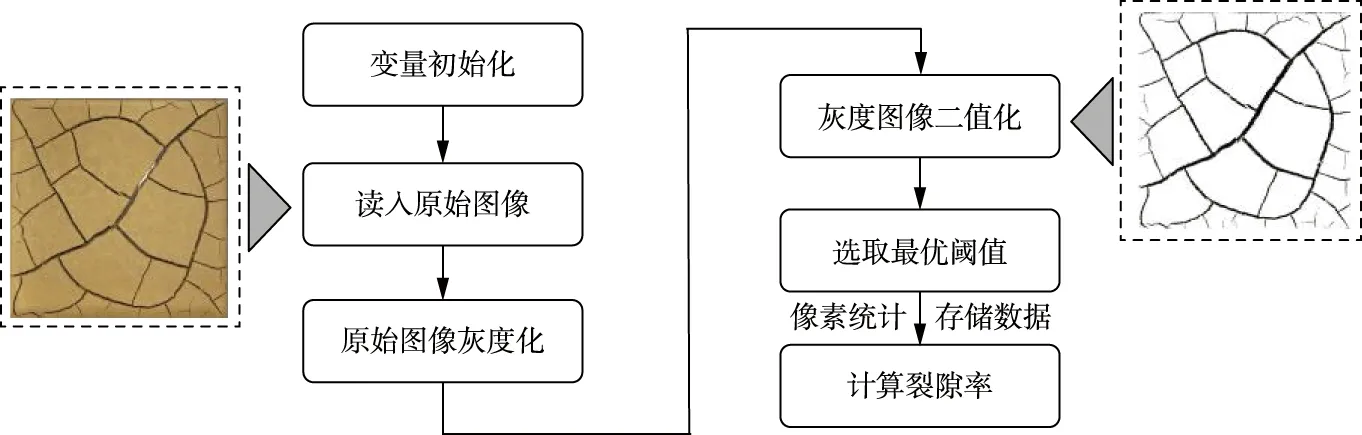
图5 裂隙率的图像二值化处理程序图

在裂隙图片的像素统计过程中，可调用MATLAB软件中的imhist函数绘制不同灰度值对应的像素值直方图(图6(a))。通过灰度图像的二值化处理，并选取最优阈值，即可得到图像处理后的像素值数据图(图6(b))，从而可用黑白(灰度值分别为0和255)像素值之比确定裂隙在试样内所占面积比例，即为试样裂隙率的实测值。

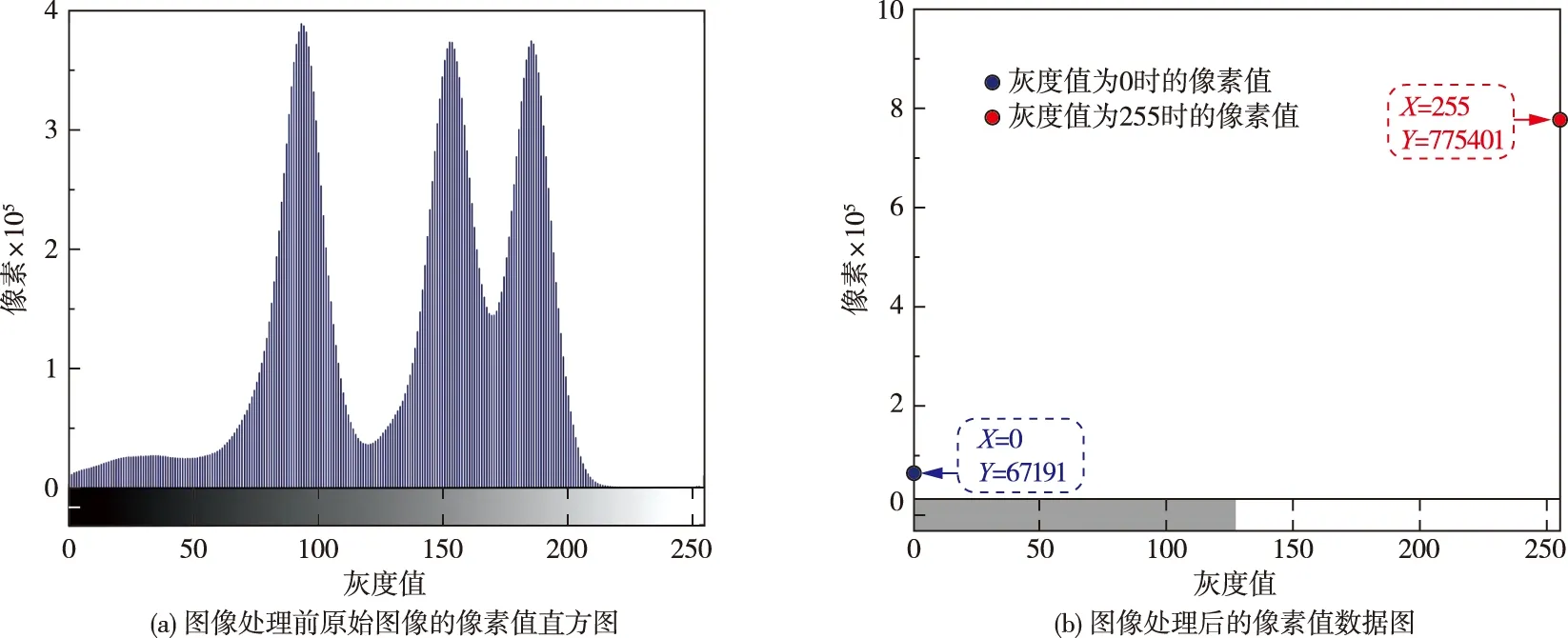
图6 裂隙图像处理前后的像素统计图

关于试样沉陷率的测算，需先在试样的干缩过程中拍摄其侧面完整照片，进而量取该照片每厘米刻度对应的像素值，再量取试样从最下端至其表面对应的像素值，取后者像素值与前者像素值之比即可确定试样表面的实际高度。采用这种方法可测得试样四边的高度，取其平均值，最后结合试样的初始高度即可确定试样沉陷率的实测值。

4.4 对膨胀土收缩-开裂-沉陷的室内试验规律预测对式(6)采用不同的拟合参数ξ和λ计算的膨胀土收缩曲线如图7所示，这两个参数虽缺乏物理意义，但对式(6)的灵敏度很高，可控制收缩曲线的不同形状。不仅如此，参数λ与土的残余收缩量或零收缩量有关，即土的这两种收缩量随λ值增大而增大；参数ξ与土的结构收缩量有关，即土的结构收缩量随ξ值增大亦呈增大趋势。此外，依据文献[34]，收缩曲线的二阶导数d2N(a)/dW2可近似确定土的结构收缩与正常收缩阶段之间、正常收缩与残余收缩阶段之间的分界点。由此，对式(6)关于归一化含水率W求二阶导可得：

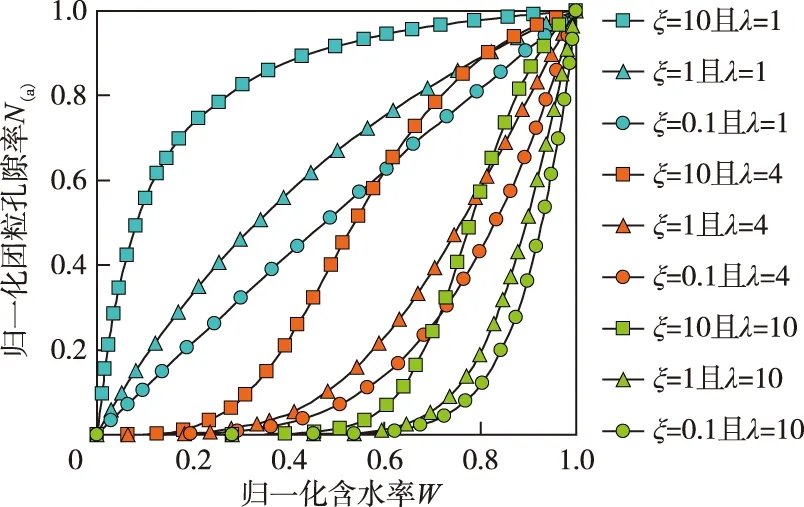
图7 参数ξ和λ取不同值时的膨胀土收缩曲线(关于团粒孔隙率)

(32)

采用文献[34]所述方法，取式(32)的负值，以便用式(32)的最小值(即图8和图9(a)中-d2N(a)/dW2的最大值)划分膨胀土的结构收缩阶段与正常收缩阶段。

采用式(6)对文献[41-42]中俄勒冈试验场与智利试验场土块的收缩试验结果进行预测，如图8所示，对这两个试验场土块的参数ξ分别取3.2和4，参数λ分别取2和1.7，式(6)对这两种土块在整个归一化含水率范围内的均方根误差RMSE分别为0.039和0.067。二阶导数d2N(a)/dS2(式(32))的负值对这两种土块在归一化含水率W=0.57和0.4时分别取得最大值，此时的W可认为是从结构收缩至正常收缩阶段的分界点。

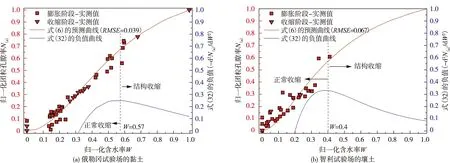
图8 俄勒冈和智利试验场膨胀土归一化的团粒孔隙率与含水率的实测关系、式(6)的预测曲线及式(32)所示二阶导数的负值)

采用式(6)(10)(17)对安康膨胀土收缩-开裂-沉陷的室内试验结果进行预测，如图9所示。由图9(a)可知，式(6)对安康膨胀土归一化的团粒孔隙率N(a)与含水率W关系预测，可得参数ξ=8.8、参数λ=2.6，式(6)对安康膨胀土在整个归一化含水率范围内的均方根误差RMSE为0.046。二阶导数d2N(a)/dW2(式(32))的负值对安康膨胀土在W=0.58时取得最大值，此时的含水率可认为是从结构收缩至正常收缩阶段的分界点。为验证本文提出的数学模型在描述安康膨胀土干燥失水收缩过程中裂隙率和沉陷率变化规律时的有效性，将式(6)所述收缩曲线的同一组参数(ξ=8.8、λ=2.6、nmax=0.459、nmin=0.281、n(s)max=0.064以及wmax=60%)代入式(10)(17)，以预测安康膨胀土归一化的裂隙率N(c)、沉陷率N(s)与含水率W关系，结果表明：式(10)(17)对安康膨胀土在整个归一化含水率范围内预测N(c)、N(s)的均方根误差RMSE分别为0.028、0.023。此外，试样减湿至不同W时对应的典型裂隙图像亦如图9(b)所示，当W=0.85时，试样表面只有一条独立裂隙，随着W逐渐减小，试样表面新生裂隙逐渐增多，裂隙开始迅速发展，交叉成网，将试样分割成若干大小不等的块区，直至W<0.23后，裂隙网络的轮廓基本定型。这组典型裂隙图像的发展趋势与文献[45]所述结论一致。

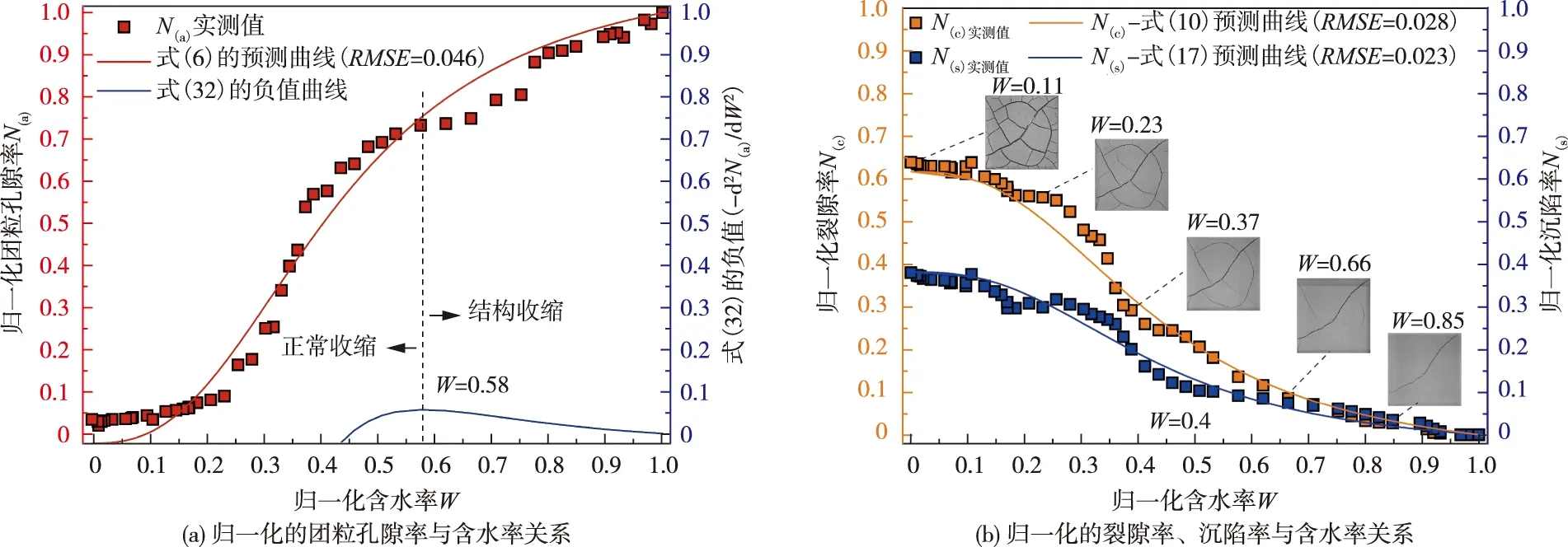
图9 安康膨胀土归一化的团粒孔隙率、裂隙率、沉陷率与含水率的实测关系、式(6)(10)(17)的预测曲线及式(32)所示二阶导数的负值

4.5 由膨胀土样的收缩试验结果预测土层的现场裂隙体积为验证本文提出的数学模型在描述膨胀土干燥失水过程不同孔隙区域变化规律的有效性，采用式(6)(10)(17)预测Hallaire[43]对膨胀土样进行的收缩试验结果，并对在现场土层的裂隙进行模拟。采用ξ=4.5、λ=3.3、nmax=0.504、nmin=0.308、n(s)max=0.045以及wmax=37.7%可得到预测曲线。对比膨胀土样的收缩试验表明：式(6)对N(a)的预测结果较其实测值的均方根误差RMSE为0.024；式(10)对N(s)的预测结果较其实测值的均方根误差RMSE为0.030；式(17)对N(c)的预测结果较其实测值的均方根误差RMSE为0.020，如图10(a)，由此可见，采用同一组参数可较为准确地模拟膨胀土样的收缩、开裂和沉陷。此外，采用同一组参数，还可预测同种土层的现场裂隙体积，式(17)对现场土层N(c)的预测结果较其实测值的均方根误差RMSE为0.063，如图10(b)。

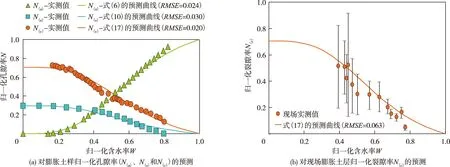
图10 采用式(6)(10)(17)预测文献[43]中膨胀土室内试验的归一化孔隙率和现场试验的归一化裂隙率

4.6 对膨胀土层的现场裂隙宽度的预测本节旨在验证式(28)所述裂隙相对宽度表达式在表征现场膨胀土层裂隙宽度随归一化含水率变化规律时的有效性。先从文献[14]所述两个试验场膨胀土层的收缩-开裂-降雨试验结果中选取1-1、1-2、2-1、2-2、2-3号裂隙为研究对象(其中1-1、1-2号裂隙和2-1至2-3号裂隙分别取自文献[14]所述的试验场1和试验场2)，进而按照如下步骤整理相对裂隙宽度与归一化含水率的实测关系：

(1)整理上述5条裂隙宽度B在降雨过程中随时间t的变化曲线，令裂隙最大宽度Bmax=B(t=0)，则可算得每条裂隙在降雨过程中不同时刻对应的裂隙相对宽度B/Bmax。

(2)采用式(29)所述van Genuchten持水曲线模型对试验场试样的饱和含水率及4.1节所述3组含水率/基质吸力实测数据进行最小二乘拟合以确定该模型的参数(图11)：αv=0.007 kPa-1、nv=4.894，相应的均方根误差RMSE为0.187。采用该曲线可将降雨过程中土层内10、20和30 cm深度处不同时刻(与裂隙宽度同时监测)的基质吸力实测值换算为相应的含水率实测值。文献[14]所述持水实测数据是在增湿过程中测得的，故拟合的持水曲线可视为边界增湿曲线。

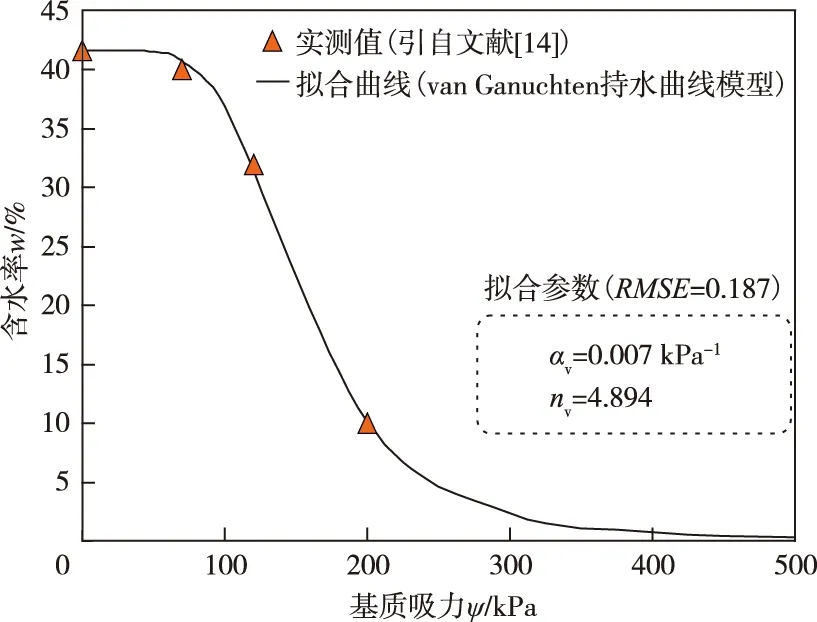
图11 文献[14]中墨西哥试验场膨胀性黏土样的持水曲线

(3)在降雨过程中，对土层内10、20和30 cm深度处不同时刻的含水率实测值求取平均值，即为w实测值。此外，由文献[14]可知入渗的雨水在土层内的储存深度为80 cm，最大孔隙率nmax=0.525，土粒密度ρs=2.65 g/cm3，故可依据wmax=ρwnmax/[ρs(1-nmax)]算得wmax=41.7%。由此可得到土层不同时刻的归一化含水率W(W=w/wmax)实测值。

综上步骤，采用式(28)所述裂隙相对宽度公式对图12所示文献[14]中上述5条裂隙的相对宽度B/Bmax随归一化含水率W变化的实测数据进行预测，相应的拟合参数分别为ξ=0.50和λ=4.15，并可看出式(28)对W=0.2～0.8范围内的均方根误差RMSE为0.090，能较好地反映裂隙宽度的变化规律。

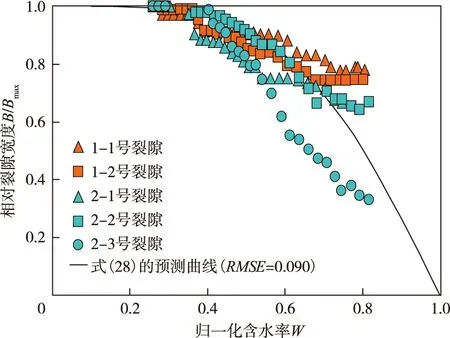
图12 采用式(28)预测文献[14]中墨西哥两个试验场的5条裂隙相对宽度B/Bmax与归一化含水率W的关系

4.7 对膨胀土样团粒孔隙率-含水率-基质吸力关系的预测虽然膨胀土的收缩量较易测定，而且可表示为含水率的函数，但膨胀土的基质吸力控制着含水率和收缩程度。为描述膨胀土团粒孔隙率-含水率-基质吸力的关系，采用已有文献[22，44]中对两种土样的这3个变量的实测结果进行对比分析，采用式(29)预测膨胀土基质吸力与含水率的关系，采用式(31)预测团粒孔隙率与基质吸力的关系，如图13—14所示，相应的拟合参数如表2—3所示。关于膨胀土样基质吸力与含水率的关系，式(29)对Reeve等[44]试验结果预测的RMSE为0.006～0.011，对Salager等[22]试验结果预测的RMSE为0.011～0.018；关于膨胀土基质吸力与团粒孔隙率的关系，式(31)对Salager等[22]试验结果预测的RMSE为0.003～0.006，对Reeve等[44]试验结果预测的RMSE为0.003～0.007。由此可见，采用6个参数(ξ、λ、av、nv、nmax和nmin)即可实现对膨胀土团粒孔隙率-含水率-基质吸力关系较好的预测。

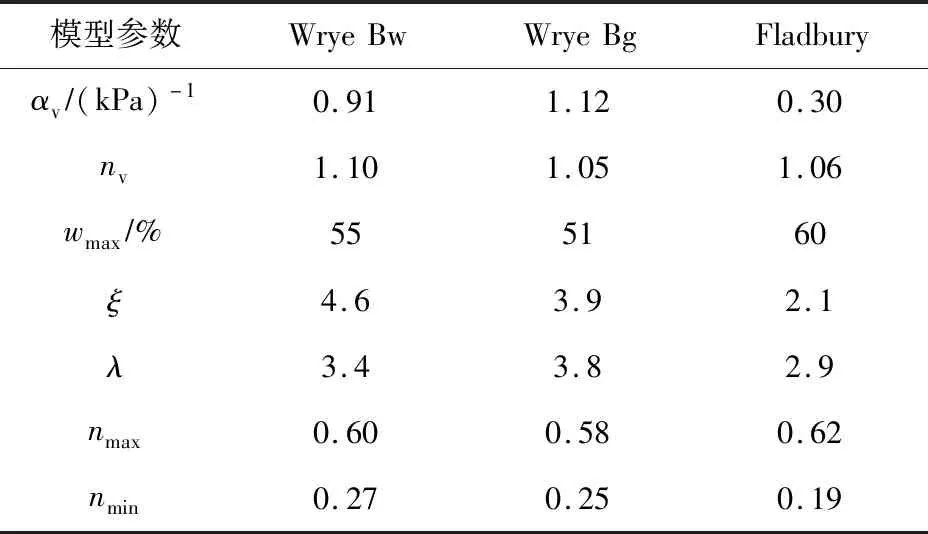
表2 模拟文献[44]中3种膨胀性黏土干燥失水收缩过程所需的参数

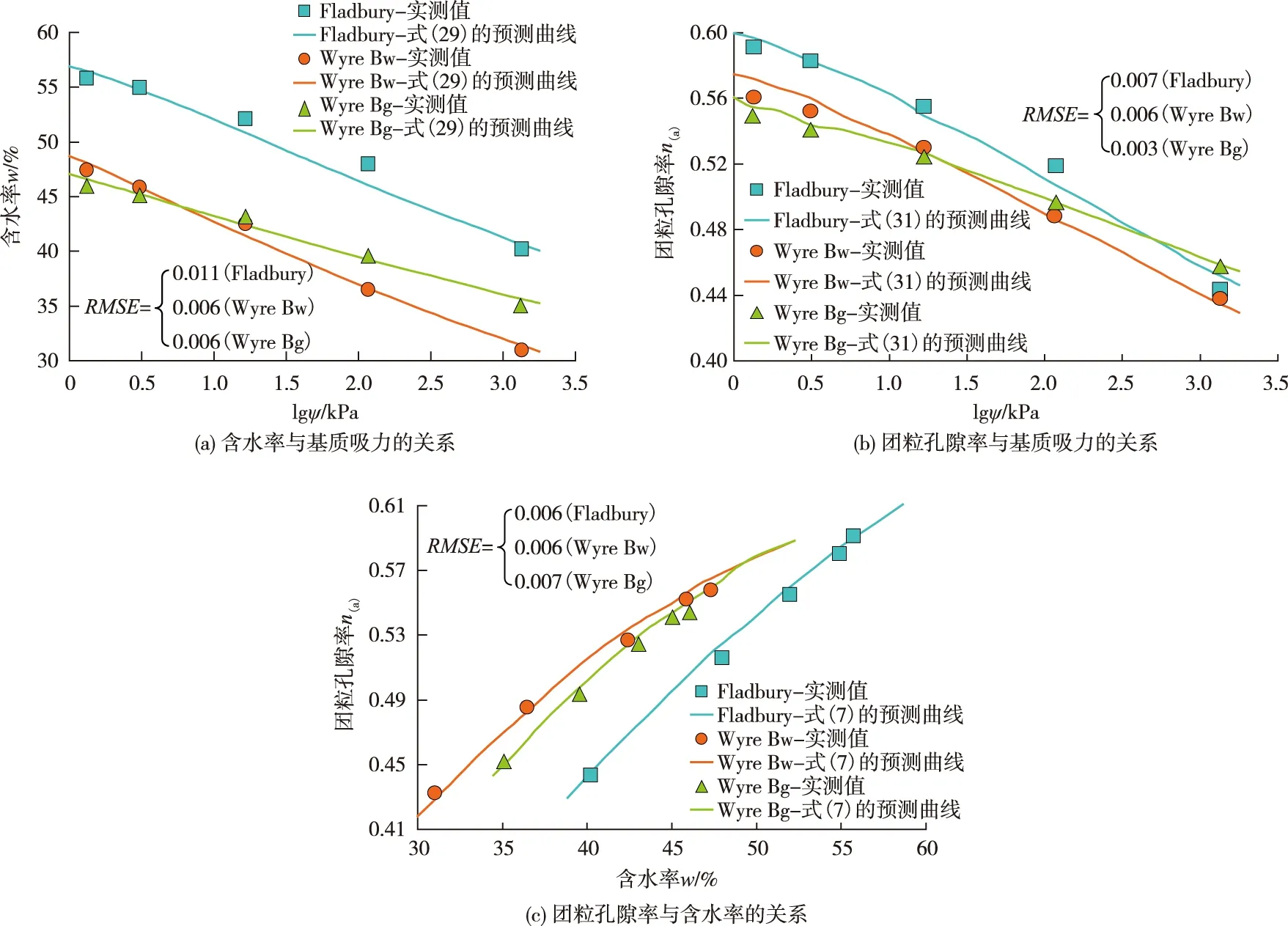
图13 采用式(7)(29)(31)预测文献[44]中膨胀性黏土样的团粒孔隙率-含水率-基质吸力关系

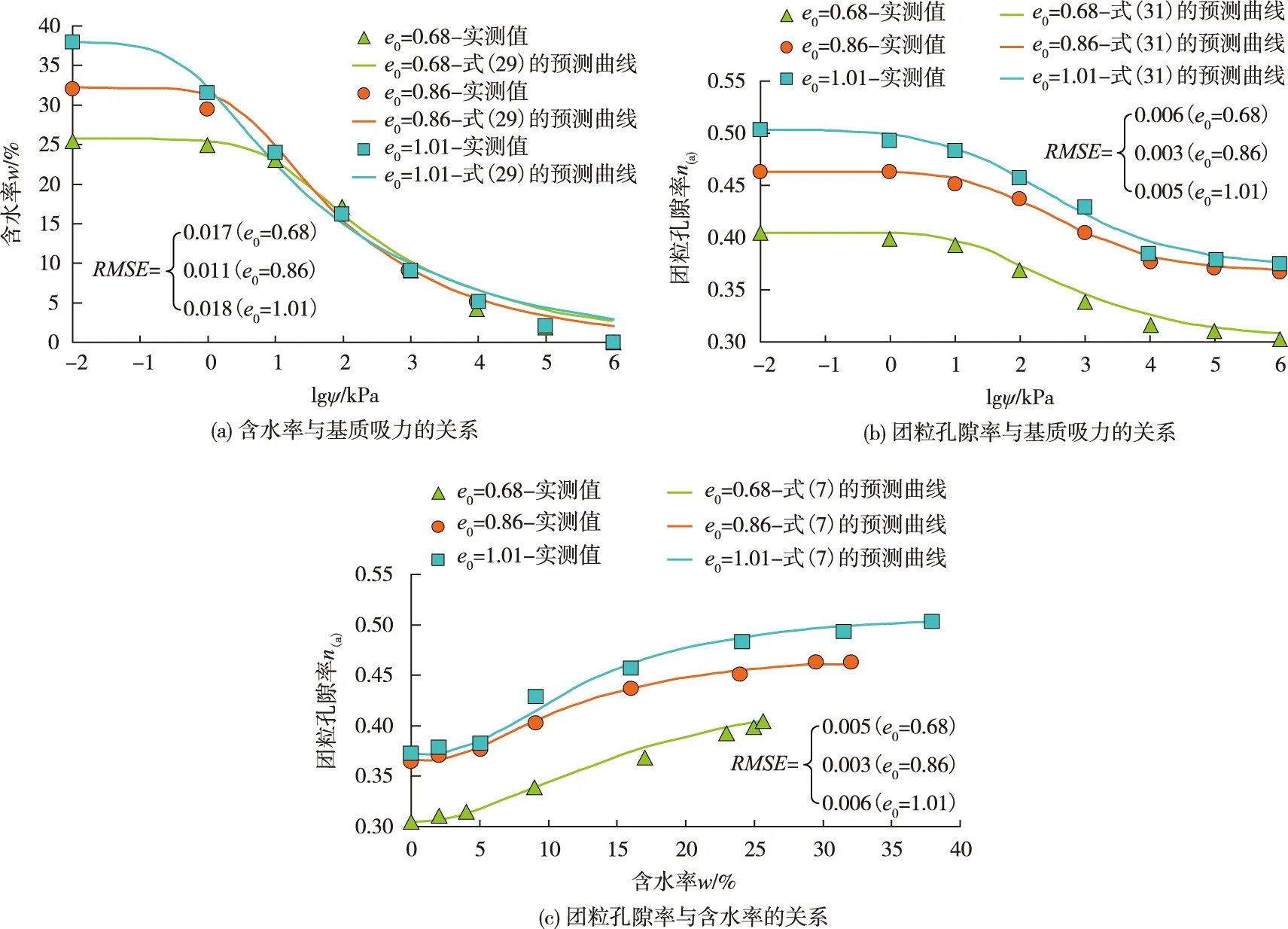
图14 采用式(7)(29)(31)预测文献[22]中含黏粉砂样的团粒孔隙率-含水率-基质吸力关系

4.8 数学模型在定量描述膨胀土渗透特性中的应用讨论已有关于膨胀土渗透系数的预测模型[20-21]和现场试验[46-48]研究表明：膨胀土的渗透特性受土层内团粒区域和裂隙区域的动态分布变化影响显著。因此，可采用本文提出的团粒-裂隙-沉陷多区域数学模型推导膨胀土渗透系数的预测模型，旨在定量描述膨胀土渗透系数随裂隙率和含水率的变化规律。具体可依据图15所述思路从以下3个步骤实现：

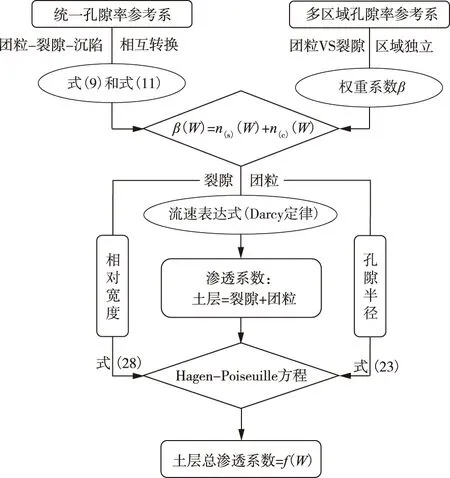
图15 本文提出的多区域数学模型在推导膨胀土渗透系数预测模型中的应用思路

(1)采用两种参考系描述膨胀土的孔隙率：一种是“统一孔隙率”参考系(本文已使用)，认为在膨胀土在胀缩过程中，其团粒孔隙率、裂隙率和沉陷率之间会相互转换；另一种是文献[49]所述“多区域孔隙率”参考系：认为裂隙区域和团粒区域相互独立。依据这两种参考系对孔隙率的定义方式，将文献[21]所述权重系数β(团粒以外区域的体积分数)表示为沉陷率n(s)与裂隙率n(c)之和，进而联立式(11)(18)可得β关于含水率的表达式。

(2)由文献[50]可知，水分在较窄裂隙内的雷诺数一般低于10，因此可假定水分在这类裂隙区域内的运动方式与团粒区域相同，均服从Darcy定律，进而将水分在这两个区域内的流速表达式与第①步中权重系数β的定义式相结合，建立土层总渗透系数与这两个区域渗透系数的关系。

(3)基于Hagen-Poiseuille方程，并联立团粒孔隙半径(式(23))和裂隙相对宽度(式(28))的表达式，即可推得土层总渗透系数关于含水率的表达式。这也是本文下一步的研究方向。

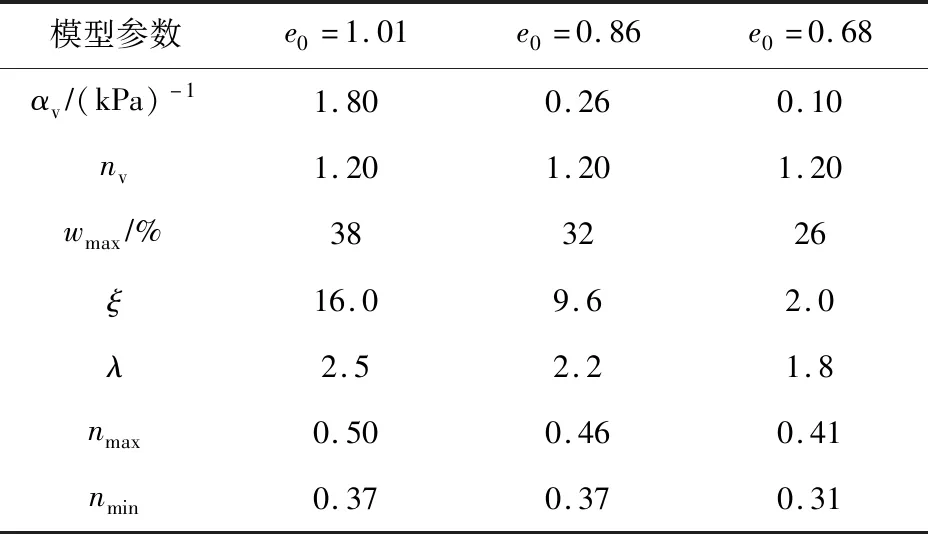
表3 模拟文献[22]中不同最大孔隙比(e0)的膨胀性含黏粉砂样干燥失水收缩过程所需的参数

5 结论

为研究干燥失水过程中膨胀土内团粒收缩与土层开裂和沉陷之间的关系，构建表征团粒、裂隙和沉陷三种区域变化规律的数学模型。主要得出以下结论：

(1)这三种区域的数学模型包含6个参数，其中wmax、ξ、λ、nmax和nmin这5个参数可采用收缩试验确定，n(s)max可通过给定收缩形状系数χ并利用该参数与nmax和nmin的几何关系算得。若认为膨胀土内团粒孔隙率的减幅与团粒外孔隙率的增幅相同，则可采用同一组参数，基于团粒孔隙率所述收缩曲线公式实现对膨胀土裂隙率及其沉陷率动态变化过程的预测。

(2)将土层中的理想土块简化为长方体，通过这些长方体的收缩来描述土层干燥失水引起的收缩-开裂-沉陷过程，进而分析该过程中理想土块与裂隙之间的几何关系，推得裂隙相对宽度的理论计算公式。

(3)对安康膨胀土开展收缩-开裂-沉陷的室内试验，并结合已有文献所述膨胀土的室内和现场试验结果，验证表明：这三种区域的数学模型在采用同一组参数时不仅对团粒孔隙率、裂隙率及其相对宽度、沉陷率变化规律的预测效果较好，而且能够较好地描述膨胀土团粒孔隙率-含水率-基质吸力的关系。本文提出的数学模型为定量描述膨胀土的体积变化特征与渗透特性提供了一种新方法。