梯级水库群多目标优化调度模型及CPF-DPSA算法研究

艾学山，郭佳俊，穆振宇，陈森林，杨百银，周鹏程

(1.武汉大学 水资源与水电工程科学国家重点实验室，湖北 武汉 430072；2.海绵城市建设水系统科学湖北省重点实验室(武汉大学)，湖北 武汉 430072；3.水电水利规划设计总院，北京 100120；4.中国电建集团昆明勘测设计研究院有限公司，云南 昆明 650051)

1 研究背景

水库群的综合效益通常包括防洪、发电、供水、航运、生态等多个方面，水库群调度需要充分协调各用水户的利益，以尽量满足水资源的综合利用需求，开展联合优化调度是发挥梯级水库群最大综合效益的主要非工程措施。而建立与各用水需求相应的多目标优化数学模型，并通过优化技术推求多目标模型的非劣解集，是解决这一问题的有效途径和方法。水库群多目标优化调度是一个多目标、多维、动态、具有多约束条件的、高度非线性的复杂优化问题，既需要合适的数学模型进行精确描述，也需要有效地获取精度高、分布广且效率高的Pareto前沿的多目标优化技术[1]。

水库群多目标优化调度模型的目标函数值主要有三种类型：一是发电量最大、经济效益最大、缺水量最小等[2-4]累积值，对该类形式的目标进行求解时，每一时段的决策可直接得出对应于目标的量值，并以调度期总的量值评判策略的优劣；二是最小出力最大、坝前最高水位最低、最大削峰等[5-7]极值，由于这类指标的值需要整个调度期的策略给出之后才能得出，在求解时需要不断地调整相应的量值，最后通过比较得到数据的最值；三是缺水率最小、出力保证率最大、供水保证率最大等[8-10]百分比，该类指标也是需要整个调度期的策略给出之后才能得到相应的数值，求解时通常对不满足基本数值(如需水量、保证出力等)要求的时段进行惩罚，使更多满足基本数值要求的决策进入到最优策略中，其各时段量级等价。

水库群多目标优化调度模型求解方法主要有两大类：(1)通过权重法、约束法、模拟统计法等将多目标问题转化为单目标问题进行求解[3，5，11]。单目标求解既包括线性规划、非线性规划、动态规划、拉格朗日松弛技术、网络流及大系统分解协调方法等经典方法，也包括人工神经网络、遗传算法、模拟退火算法、蚁群算法和粒子群算法等人工智能算法。但权重法的权重难以科学确定、各目标的优化进度不清晰；约束法难以确定次要目标的约束限值；模拟统计法没有体现出最优化的特点、且计算效率较低。同时，非劣解集性能依赖于单目标求解的方法以及目标转化的策略，精度可以通过令人满意的单目标算法得到保证，但为了得到多个代表性的非劣解组成非劣解集，效率往往会偏低；(2)运用以Pareto理论[1]为基础的多目标进化算法(MOEAs)进行求解。进化算法具有鲁棒性和分布多样性的特点，在各领域应用广泛[12-14]。进化算法主要集中在多目标个体的优选和解的分布两类问题，常见的有基于Pareto支配关系和拥挤度/参考点机制进行多目标寻优的NSGA-Ⅱ/Ⅲ算法[15-18]、采用基于Pareto强度和k邻近(KNN)分类方法进行密度估计[5]的SPEA/SPEA2算法[19-20]、采用Archive(“档案”)集记录保存当前搜索到的非劣解和自适应网格控制解分布的MOPSO及其改进算法[21-24]等。进化算法对一些复杂的长系列优化问题，很难获得均布的Pareto前沿，且没有有效的算法终止准则，且在理论上不能保证获取分劣解。为了使非劣解集的分布均匀，常采用给定的一组各不相同的权重，将多目标通过传统加权和权重方法、边界交叉点方法或者切比雪夫分解方法等策略进行转化，分解得到一组单目标问题，再采用进化算法求解[25-26]。由于进化算法固有的随机不可控的特征，难以保证算法收敛后是否能够获得真正的、分布足够均匀、广泛的非劣解集。

综上所述，水库群多目标优化调度主要存在两个方面的问题：一是如何根据水库群的实际需要，选择合适的多个目标、确定目标函数值类型；二是兼顾计算效率(速度快)和非劣解集质量(广泛、均布)的多目标求解算法。针对这两个问题，以老挝南欧江梯级水库群为实例，选取累积值、极值及百分比等三种目标函数，建立梯级水库群多目标联合优化调度模型，提出基于惩罚因子的动态规划逐次逼近法(CPF-DPSA)对多目标模型进行求解，并通过与动态规划逐次逼近法(DPSA)和第三代快速非劣排序遗传算法(NSGA-Ⅲ)的对比分析，以验证该算法的性能和解的效果。

2 梯级水库群多目标优化调度数学模型

2.1 目标函数以具备发电任务的梯级水库群调度为例，一般具有三种主要需求：一是追求自身效益最大；二是必须承担部分社会责任；三是保证河流生态健康。针对这三种需求，分别以梯级总发电量最大、梯级最小出力最大和梯级生态断面用水保证率最大为目标函数。

(1)梯级总发电量最大：

(1)

式中：E为调度期内水库群的总发电量，kW·h；Ni(t)为t时段i水库的出力，kW；Ki为i水电站的出力系数，i=1，2，…，I；I为电站总数；T为调度期总时段数，时段序数t=1，2，…，T；Qfd，i(t)为i水电站在t时段的发电流量，m3/s；Hi(t)为i水电站在t时段的发电水头，m；Δt为t时段以小时为单位的计算时段长，h。

(2)梯级最小出力最大：

(2)

式中：Nmin为T个时段内梯级最小出力，kW；NS(t)为t时段的梯级总出力，kW。

(3)梯级生态断面用水保证率最大：

(3)

(4)

式中：Pe为梯级生态断面用水保证率，是指水库群在调度期各时段内，生态断面上游水库(序号b∈[1，I])出库流量Qck，b(t)不小于生态流量Qe，b的时段数与全部时段数的比例， %；edes为生态需水破坏次数；ψ(t)表示在时段t是否满足生态流量，满足时为0，不满足时为1。

2.2 约束条件式(1)—(4)必须满足如下约束条件：

(1)水库水量平衡约束：

(5)

(2)水库水位约束：

(6)

(3)出力约束：

(7)

(4)边界约束：

(8)

(5)流量约束：

(9)

(6)非负约束：各变量非负。

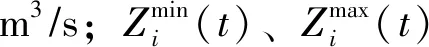
3 模型求解

3.1 基础算法动态规划逐次逼近法(DPSA)是一种有效的降维方法[27]。它采用逐次迭代逼近的思想[28]，将一个多维问题分解为多个一维问题求解。DPSA求解时，从一条初始调度状态线出发，先假定其它水电站运行状态不变，从最上游水电站开始，每次仅对一个水电站采用动态规划(DP)求解，然后更新该水电站的运行状态及泄流信息，再进行下一个水电站的DP计算，这样依次对每个水电站进行寻优，不断更新各个水电站的最优调度策略，循环迭代直至目标不能继续改进为止，所得的最终调度策略即为通过DPSA求得的最优策略[29]。

DPSA基本步骤如下：

(1)基本资料输入：输入的数据包括水库库容曲线、出力系数、水库的上下游拓扑关系、龙头水库的入库流量、各区间的入流和各电站初始条件等；

(2)初始轨迹生成：应用DP算法从上游到下游依次计算各水库的最优轨迹；

(3)迭代计算：保持其它水库运行状态不变的情况下，每次对一个水库进行库容离散，运用DP进行优化；

(4)更新水库优化后的库容、水位、出库流量等运行状态；

(5)用DP继续优化下一个水库，直到遍历完梯级的所有水库，计算梯级水库综合目标值，进行下一次迭代计算；

(6)不断重复(3)以后的步骤，直到目标函数值已经基本稳定为止，输出求解结果。

3.2 改进算法采用惩罚因子对其他目标(f2、f3)建立惩罚函数并加入到累积值目标(f1)，将水库群多目标问题转化为单目标进行求解，该方法称为基于惩罚因子的动态规划逐次逼近法(the DPSA Based on Combination of Penalty Factors，即CPF-DPSA)。其计算流程与DPSA大体一致，但需做如下处理：

(1)DP状态转移方程。在计算初始调度线时，DP顺序递推算法的寻优递推方程为：

(10)

在迭代计算时，使用DPSA算法的寻优递推方程为：

(11)

式中：Eother，l(t)为t时段除i以外的其他水电站在原先调度线上，运行状态不改变情况下计算所得的发电量，由于当前时段i水电站的不同决策会影响出库流量，故而下游所有水电站同时刻都会受到影响，上游若受回水顶托也会有所影响，因而在寻优时考虑该项；o1、o2为对应于目标f2、f3的惩罚因子，取非负数；R1(t)、R2(t)为t时段对于目标f2、f3的惩罚基本量，可应用不同的惩罚策略：

①线性型。可认为每一时段对应目标的破坏是不等价的，考虑计算值与基本量的不足程度，表示为线性变化，如对最小出力的惩罚，可采用如下线性公式计算：

R1(t)=Nd-NS(t)t=1～T

(12)

式中：Nd为高于Nmin的设计值，依此判断本时刻梯级总出力NS(t)的基本惩罚量。

②非线性型。可认为每一时段对应目标的破坏是不等价的，依据计算值与基本量的不足程度来评判惩罚量级，不足程度越大，惩罚力度越大，表示为非线性变化，如对最小出力的惩罚，也可采用如下指数型惩罚公式计算：

R1(t)=aN(t)/Nd×(Nd-N(t))t=1～T

(13)

式中a为底数，根据实际情况取适当值。

③常数型。可认为每一时段目标的破坏是等价的，不考虑破坏深度，如对生态目标，其惩罚基本量可以常数的形式表示：

R2(t)=ψ(t)

(14)

(2)惩罚因子(o1，o2)取值。一般地，一组惩罚因子有可能得到一个多目标的非劣解，为了获得分布较为均匀、广泛、真正的非劣解集，必须对(o1，o2)的影响范围和离散宽度做出判断。惩罚因子代入CPF-DPSA时分两阶段策略：

第一阶段：惩罚因子影响范围探测：

①点绘f2-o1、f3-o2曲线；

②考查曲线变化趋势，分析排除接近于无影响区域得到惩罚因子的影响范围区间S1和S2，保证在有效范围内确定因子取值；

③在S1和S2中，根据目标随因子变化的梯度选取因子离散值：在变化剧烈处可多选点，在变化平缓处适量减少选点，得到相应的惩罚因子取值范围集合s1和s2，对应元素个数为d1和d2。

第二阶段：组合s1和s2得到数量为d1×d2的取值空间，对组合中的每一个元素逐个代入CPF-DPSA求解非劣解，经过多目标筛选后得到非劣解集。

CPF-DPSA算法的流程图以及梯级水库群多目标优化调度问题求解思路如图1和图2所示。

图1 CPF-DPSA算法流程图

图2 梯级水库群多目标优化调度问题求解思路

3.3 评价指标在分析所得非劣解集的优劣时，需考虑其收敛性和分布的多样性，并与其他算法比较[30]。

(1)采用超体积指标[19](HV)来衡量个体所支配的空间，以综合评估解集A的收敛性和多样性：

(15)

(16)

式中：zref为设定的参考点，一般为Pareto最优解集中各个目标上的最差值组成一个新的点；ci为由某一非劣解xi对应的前沿点与zref作为对角线构成的超立方体，其超体积为volume(ci)；fk(xi)为xi对应前沿点的第k维坐标值，即该非劣解对应的第k个目标值，目标总数为M。

(2)采用解集覆盖率指标[31]C来衡量的是两个解集之间的重合程度，可用于比较不同算法所得非劣解集的优劣：

(17)

式中：分子为B中被A中至少一个解支配的解的数目；分母为B中包含的解的总数。

C(A，B)=1为B中所有解都被A中的一些解所支配，C(A，B)=0为B中没有解被A中的任一解所支配。指标C越大，代表解集A的质量较解集B越好。

4 实例分析

4.1 南欧江流域梯级水库群概况南欧江发源于中国云南省江城县与老挝丰沙里省接壤地区，是湄公河左岸老挝境内最大的一条支流，如图3所示。河流自北向南，在琅勃拉邦市附近汇入湄公河，流域面积2.56万km2，河道全长475 km，天然落差约430 m，水能指标优良，是老挝政府极力推进开发的水能资源基地之一，目前规划建设的7个水电站将陆续投产运行。南欧江梯级各水电站主要特征参数见表1。

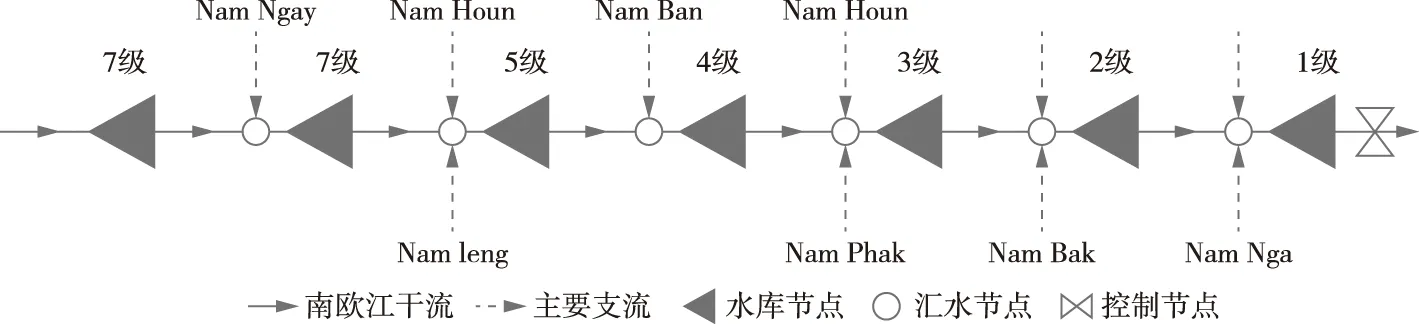
图3 南欧江流域水电站群拓扑图

表1 南欧江梯级各水电站主要特征参数表

基于南欧江流域1959—2013年共55年的历史入流资料、各水电站水库特征参数，选取梯级总发电量最大、梯级最小出力最大和梯级生态断面用水保证率最大三个目标，进行长期联合优化调度计算。调度期起止水位均取死水位以上到正常蓄水位的三分之二处，梯级联合保证出力Np为337.07 MW，生态控制断面取站群最下游，生态流量取200 m3/s(实际南欧江流域无生态流量要求，且按一般10%或汛期30%多年平均流量作为生态需求对该流域较容易满足)。

4.2 CPF-DPSA算法优化调度求解运用Microsoft Visual Studio C#编写以发电量E最大为目标的CPF-DPSA算法程序，水库状态离散步长取0.1 m，选取惩罚因子参数为(o1，o2)，分别对应梯级最小出力Nmin和梯级断面生态流量保证率Pe目标的惩罚系数。对Nmin采用指数型惩罚策略进行控制：Nd取1.2Np，a取100，以此避免小的出力，例如(0 MW，100 MW)相比(50 MW，50 MW)惩罚量大。对Pe采用常数型惩罚策略，表示每一时段的破坏等价，且不考虑破坏深度。

先进行第一阶段的惩罚因子影响范围探测，研究各目标随单一因子的变化情况，单一惩罚因子对相应目标值的变化关系情况如图4所示。

图4 各目标值随某单一惩罚的因子变化关系

从图4可以看出：

(1)随着惩罚因子的增大，对应最小出力和保证率目标值相应增大，体现出了“惩罚”的作用，该梯级水库群当o1≥1000～3000时，最小出力Nmin最大值渐渐收敛于376.936 MW，当o2≥800后，生态断面用水保证率Pe的最大值收敛于100%。

(2)越靠近原点，对应目标值变化越快，至远端则几乎不受惩罚影响，由此，可以筛选组合两个惩罚因子的取值范围：取o1∈S1=[0，3000]，o2∈S2=[0，1000]。

相应地，根据图4变化趋势，均匀离散组合s1×s2，进行第二阶段操作。

为了获得尽可能多的非劣解，以便于更好的拟合三维曲面，本例共求解了2088个组合，除去劣解，最终得到的非劣解集421个，并拟合Pareto前沿面PFC，如图5所示。另外根据所有点的分布情况分析三个目标之间的竞争关系(如图6)：

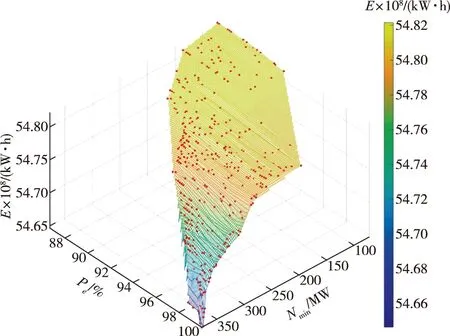
图5 CPF-DPSA非劣解集拟合(线性)前沿面(PFC)

图6 CPF-DPSA解集目标间分布关系

(1)由图6(a)(b)，梯级发电量E与梯级最小出力Nmin和梯级生态断面用水保证率Pe均有竞争关系，出力形式的竞争较为激烈，对生态流量Pe的竞争程度较轻，与文献[3，22，24，28]的结论一致。

(2)由图6(c)，Nmin与Pe有一定的协同关系，从机理上表现为：随着最小出力的增大，发电流量随之增大，因而生态流量更能得到保证。尤其，图中点划线矩形区域表示在Pe≥93%时，Nmin会自然而然地受到控制，突变提升至170 MW以上，这与枯水期某关键控制时刻有关，更加反映了Nmin与Pe的密切协同关系。

4.3 结果比较与分析为了评估和验证CPF-DPSA算法对梯级水库群多目标优化调度模型求解的适用性与性能，可以与DPSA算法和NSGA-Ⅲ算法的求解结果进行比较和分析。

基础的DPSA算法对于梯级水库群的联合优化调度往往具有较高的精度，但主要针对单目标优化，因而根据多目标中各个单独的目标来进行DPSA寻优，多少个目标就可得到对应的多少个解。实际应用中，对于极值形式的目标Nmin，其结果受初始解的影响较大，故在长系列计算中比较了几个典型的初始解(高水位、低水位、平水位和随机等)得到的结果。

在采用NSGA-Ⅲ算法对原问题进行求解时，选取的锦标赛规模为2，采用实数编码、模拟二进制交叉和常规多项式变异：交叉分布系数为15，变异分布系数为20，种群规模为300，参考点数为210，进化代数100 000。得到的结果PFN如图7所示，从坐标轴值上看，结果点较为集中，各目标值较为接近，在其具体优化过程中表现为3个目标沿某一方向的集体优化(如图8)，且速度渐缓。由于相比PFC，PFN各目标极为相近，选取各目标值的最值解作为代表参与比较。

图7 NSGA-Ⅲ非劣解集点的分布

图8 NSGA-Ⅲ某一个体进化过程

将DPSA各单目标解、NSGA-Ⅲ代表解和CPF-DPSA中根据PFC选取的典型解(如图9)进行比较，如表2所示。

图9 CPF-DPSA典型解

表2 三种算法典型非劣解比较

由图5—9和表2可知：

(1)CPF-DPSA算法是在DPSA基础上引入惩罚因子组合的策略，综合求解梯级水库群多目标联合优化调度问题。相比于DPSA仅能求几个特定非劣解，CPF-DPSA算法可通过人为控制离散的惩罚因子组合，得到大量解并提取令人满意的非劣解集，其分布较为均匀，精度可以达到要求。相对地，由于保留精度(3位小数)、离散步长、多目标的叠加作用、以及保证率形式(计算最小单位为总时段的倒数)影响，CPF-DPSA的非劣解效率可达20%(421个非劣解/2088个所求解)。由此可见，CPF-DPSA算法可以稳定可靠地完成多目标优化模型的求解。

(2)对比图5和图7坐标轴值、差值及点的位置可知，CPF-DPSA算法较NSGA-Ⅲ算法非劣解解集点分布的范围更加广泛，目标值更加优秀。另外考查两个算法的超体积指标HV和解集覆盖率指标C(如表3)，其中为使PFN与PFC便于比较，对PFN∪PFC进行了极值法的归一化处理，因此有相对超体积指标满足0≤HV≤1且zref=(0，0，0)。

表3 CPF-DPSA与NSGA-Ⅲ非劣解集的指标结果对比

由表3可知：

a)HV越接近1，相应地非劣解前沿面越饱满，解集的收敛性和分布性越好。CPF-DPSA所得非劣解集(0.866)综合性能较好，而NSGA-Ⅲ(0.253)较差，且前者远优于后者。

b)计算CPF-DPSA所得PFC与NSGA-Ⅲ所得非劣解集的PFN之间C(PFC，PFN)=1，即尽管PFN中解与PFC的某些解相比非劣，但其所有解都可在PFC中找到某一解支配它。具体而言，随意选取PFC中较典型的几个解与PFN中的某一解(由于各目标相近，仅取一个代表)比较，结论可从图7和表2看出：PFN中的解Ⅱ与PFC的解①—③和⑤—⑧相比，均表现为非劣解的特性，但PFC中的解④却可以支配它，因此解Ⅱ成为了劣解。相应地，针对其他PFN解，在图5中均可找到这样的PFC解来支配它。

综上所述，CPF-DPSA计算的非劣解较为准确，而NSGA-Ⅲ迭代100 000代所得解集的PFN均是较PFC的劣解，收敛、分布效果不佳，综合他人研究成果[32]，其原因在于NSGA-Ⅲ算法在一般解决时段较短问题(如代表年、典型年、时期等)时效果良好，而在解决长达55年的多目标水库调度问题时，由于总时段数为660，个体实数编码长为4620，致使在进行交叉、变异时面临巨大的寻优空间，其优化收敛较慢，使得计算所得的各点目标值差距较小，如图7所示。将PFN置于PFC中，PFN仅为PFC中的一个小角落，故基于参考点的策略在水库群多目标的长系列优化调度效果不太理想，应用NSGA-Ⅲ算法求解该问题还有待研究改进。相比之下，CPF-DPSA算法基于DPSA在精度上有保证，且在解的分布上可进行人为的区域控制，从而能够更好地解决梯级水库群多目标优化调度问题。

5 结论

(1)以梯级水库发电量最大、最小出力最大和生态断面用水保证率最大分别代表累积值、极值及百分比等三种主要目标函数型式，构建的多目标优化模型对于梯级水库群优化调度具有普适性。

(2)提出的基于惩罚因子的动态规划逐次逼近法(CPF-DPSA)，可有效控制惩罚因子的选取范围，避免惩罚因子选取的不确定性问题，且可获得分布均匀、广泛的非劣解集，比DPSA适用条件更广，比经典多目标进化算法NSGA-Ⅲ的精度高、分布性好、稳定性佳，同时揭示NSGA-Ⅲ算法在长系列多目标水库群优化调度模型求解方面仍待进一步研究。