遥感和再分析蒸散发数据精度评估：基于GRACE和流域月水量平衡模型的比较研究

云兆得，胡庆芳，2，王银堂，2，吴海燕，王磊之，商守卫

(1.南京水利科学研究院 水文水资源与水利工程科学国家重点实验室，江苏 南京 210029；2.长江保护与绿色发展研究院，江苏 南京 210098；3.湖州市水利局，浙江 湖州 313000)

1 研究背景

地表蒸散发(Evapotranspiration，ET)是指水分以蒸发和蒸腾方式散失到大气中的过程，是大气圈、水圈和生物圈水分和能量交换的基本过程之一，是水循环过程的重要组成部分。准确估算蒸散发对于认识全球或流域水分、能量平衡关系至关重要，也是流域水资源管理、干旱监测评价和生态保护修复等一系列工作的重要基础[1-3]。闪烁仪、蒸渗仪、涡动相关系统和通量站等传统观测方式[4]可较准确提供点尺度蒸散发信息，但无法有效获取区域蒸散发空间分布。近20年来，遥感蒸散发反演技术获得很大进展，使得流域空间化蒸散发数据的获取成为可能。基于不同反演模型和算法，国内外已研制了一系列长时序遥感蒸散发格网数据集，如基于Penman-Monieth(PM)模型的MOD16数据(Moderate Resolution Imaging Spectroradiometer 16)[5]，基于Priestley-Taylor模型(PT)的GLEAM(the Global Land Evapotranspiration Amsterdam Model)[6]和基于地表能量平衡模型的SSEbop(Simplified Surface Energy Balance Model)[7]等等。同时，GLDAS(Global Land Data Assimilation System)[8]和CLDAS(China Land Data Assimilation System)[9]等陆面数据同化系统通过融合卫星遥感和地面观测资料，也提供了网格化的地表蒸散发再分析数据。

遥感反演或再分析数据可反映陆面蒸散发的复杂空间异质性，为定量解析流域水分和能量过程创造了条件。然而，陆面蒸散发过程十分复杂，这些数据不可避免地受到卫星观测方式和反演算法局限性的影响，对于地表“真实”蒸散发的表征具有不确定性，因此开展蒸散发数据精度的地面验证和评价十分必要。但具有较完备的蒸散发地表观测信息或开展野外科学试验的流域尚不常见。因此，若干文献假定流域水储量变化为零，然后由降水和径流观测资料计算实际蒸散发，以此作为基准数据[10-11]，然而即使在多年时间尺度上流域水储量变化为零的假定也可能并不满足，同时这种方法也不能应用于较小的时间尺度上。因此，大量研究结合地球重力卫星GRACE(Gravity Recovery and Climate Experiment)反演的陆地水储量变化和流域降水、径流观测数据，通过水量平衡方程建立蒸散发基准序列。采用这种方法，Madeleine等[12]估算了美国境内11个主要流域的实际蒸散发，评估了5种陆面模式和3种遥感反演蒸散发数据的效果，发现多种数据集的估值结果均显著低于基准序列，且对于实际蒸散发季节性变化特征的捕捉较差。类似地，Rodell等[13]在美国、非洲等地的7个代表性流域比较了多种遥感反演和再分析实际蒸散发数据的精度，发现这些数据各有优势，并无绝对优劣。Tian等[14]的研究表明采用GRACE水储量变化数据估计的长江流域上中下游实际蒸散发，与MOD16蒸散发数值的吻合程度要高于GLDAS-Noah 等3种GLADS再分析蒸散发数据。

受观测方式、传感器性能等因素影响，GRACE数据存在重力场及南北方向上的条带噪声误差[15]，这些因素在一定程度上增加了陆地水储量变化信息的不确定性。同时，GRACE数据观测周期也会影响陆地水储量变化的精确性。目前已提出了多种改进算法[16-17]。然而无论是否采用这些改进算法，基于GRACE数据和水量平衡方程推算的流域实际蒸散发序列均可能存在不合理之处[13-14，16，18]，甚至会出现月实际蒸散发量为负值的情况，这一情况必然影响遥感或再分析蒸散发数据精度验证和评价的可靠性、真实性。事实上，随着多源数据联合反演算法的快速发展，大量卫星遥感和再分析蒸散发资料纷纷涌现，科学验证和精度评估验证已成为一个重要的基础性问题。鉴于此，本文尝试采用流域两参数月水量平衡模型WBM-DP(Water Balance Model with Double Parameters)和GRACE水储量变化量数据分别构建流域实际蒸散发序列，以此探究不同基准序列对代表性遥感和再分析蒸散发数据精度验证结果的影响，从而为全球或区域蒸散发反演算法的改进、数据集研制和基于全球性资料的流域水循环过程模拟提供参考。

2 研究方法

2.1 流域蒸散发基准序列构建方法

2.1.1 基于GRACE水储量的构建方法 对于某一闭合流域而言，某一月份流域实际蒸散发ETt，GRACE可由以下水量平衡方程计算得到，即：

ETt，GRACE=Pt-Qt-ΔSt

(1)

式中：Pt为第t月流域面平均降水量，mm，根据较高密度的地表雨量站网观测信息经空间插值得到，或采用地表数据校正后的卫星遥感或再分析资料估计；Qt为第t月流域实测径流深，mm，可由流域出口断面水文站观测得到；ΔSt为第t月初末流域水储量变化量，mm，ΔSt=St-St-1，直接由GRACE水储量数据得到。为表述方便，本研究中将基于GRACE水储量变化数据和式(1)推求的流域蒸散发月序列记作ETGRACE。

2.1.2 基于WBM-DP的构建方法 基于WBM-DP的流域蒸散发序列构建方法同样建立在式(1)的基础上，但对ΔSt等各分量的处理方法不同。WBM-DP由3组方程构成：①流域水量平衡方程，即式(1)，用于描述某一时段流域水储量变化与各源汇项间的关系；②水热耦合平衡方程，用于描述水分和能量因素共同控制下的流域实际蒸散发；③流域蓄泄方程，用于计算流域出口断面径流量。

月尺度的流域水热耦合平衡方程如式(2)所示，该方程基于Budyko假说[19]经数学推导得到，其有效性已得到大量验证[20]：

(2)

式中：ETt，WBM为第t月模拟实际蒸发量，mm；Ht为第t月可供蒸散的总水量，mm，Ht=St-1+Pt，为流域月初水储量和本月降水量之和；PETt为第t月的潜在蒸散发，mm，本研究采用FAO56 PM公式[21]计算的参照腾发量为代表；n为模型的第1个参数，是反应流域下垫面特性的参数，与流域地形、植被和土壤等大量因素相关，各月采用相同值。

流域蓄泄方程如式(3)所示：

Qt，WBM=(Ht-ETt，WBM)2/SC

(3)

式中：Qt，WBM为第t月模拟流域径流深，mm；SC为模型的第2个参数，可理解为流域蓄泄系数，各月采用相同值。

联立式(1)—(3)，即可进行逐月水量平衡计算，从而得到月径流量、蒸散发以及流域蓄水量连续过程。WBM-DP的两个参数n和SC采用流域出口断面径流资料率定。本文将WBM-DP推算的流域蒸散发序列记作ETWBM。

2.2 流域蒸散发精度评价指标采用绝对值平均误差(Mean Absolute Error，MAE)、相对的绝对值平均误差(Relative Mean Absolute Error，RMAE)、中心化均方根误差(Centered Root Mean Square Difference，CRMSD)和相关系数(Correlation Coefficient，CC)项指标，在月尺度上评价汉江流域上游卫星遥感和大气再分析蒸散发数据的精度。4项指标计算方法如式(4)—(7)所示：

(4)

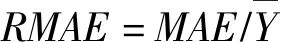
(5)

(6)

(7)

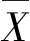
3 研究区域和数据

3.1 研究区域本文以汉江流域上游，即丹江口水库控制流域为研究范围。该流域是南水北调中线工程和引江济渭两项跨流域调水工程水源地，在全国水资源配置中具有重要地位。地理位置介于106°12′E—111°26′E和31°24′N—34°11′N(图1)，跨陕西、湖北和河南三省，流域面积约9.5万km2，约占汉江流域面积的60%。研究区域地处秦准、大巴山和米仓山等山脉之间，地形复杂，海拔介于127～3467 m。多年平均降水量约为900 mm，多年平均水面蒸散发量约1180 mm，多年平均径流量约393.4亿m3。降水和径流年内分布不均，7—10月径流量占全年的60%左右。

3.2 数据资料

(1)蒸散发数据。收集整理了2006—2014年的汉江流域逐月气象观测和实际蒸散发数据。潜在蒸散发由流域内19个国家气象站常规地表观测资料，采用FAO56 PM公式计算得到，进一步利用反距离权重法插值得到流域面平均逐月潜在蒸散发，作为WBM-DP逐月水文模型的输入因子之一。

本文采用的2种遥感反演和1种大气再分析实际蒸散发数据的基本情况如表1，三者分别为基于3种不同蒸散发算法的代表性数据，其中MOD16采用PM模型；SSEbop基于简化地表能量平衡模型；Noah基于陆面同化系统。

(2)降水数据。获取了2006—2014年汉江流域MSWEP(Multi-Source Weight Edensemble Precipitation)[23]月降水格网数据集。MSWEP是一套集成卫星遥感、大气再分析信息的全球性降水数据集。本文根据汉江流域505个雨量站观测值，利用地理加权回归方法[24]对MSWEP数据进行校正，得到了汉江流域上游逐月面平均降水量。

(3)径流数据。从水利部刊印的水文年鉴(第6卷第14册)，获取了2006—2014年丹江口水库坝址下游汉江干流的黄家港水文站逐月径流量，并根据丹江口水库水位-库容特征曲线等资料推求了丹江口水库逐月入库径流量。

(4)陆地水储量变化数据。获取了美国德克萨斯大学奥斯汀分校CSR(Center of Space Research，CSR)[25]基于GRACE重力卫星观测数据[26]研制的陆地水储量变化数据，空间分辨率为0.25°，该数据所使用的球谐方法较标准方法具有更好性能[27]。据此提取了汉江流域上游2006—2014年逐月的陆地水储量变化量，个别月份缺失数据通过相邻月份线性插补得到。

4 结果分析与讨论

4.1 流域水储量变化比较由于流域水储量对蒸散发基准序列的构建均有影响，从而影响蒸散发数据集的精度评价结果，因此首先对GRACE数据和WBM-DP模型得到的流域水储量进行了比较。图2给出了2006—2014年基于WBM-DP的汉江流域上游月径流和水储量过程模拟结果。由图2(a)可知，WBM-DP得到的入库径流模拟过程与实际径流过程吻合较好。在率定期，WBM-DP水量模拟相对误差BIAS和纳什效率系数NSE分别为0.00和0.83；在验证期，BIAS和NSE分别为0.09和0.73，虽然精度有所降低，但尚可接受。这与前人研究基本一致，即月水量平衡模型在湿润区一般具有较强适用性。由图2(b)可知，汉江流域上游水储量在年内一般呈单峰分布、峰谷相间，与降水具有较强同步性。随着雨量增加，流域水储量也相应增加，在汛期达到峰值；而在峰值过后，由于降水补给小于蒸散发消耗和径流外排量，故流域水储量又不断减少，直至在年末或次年初达到最低值。

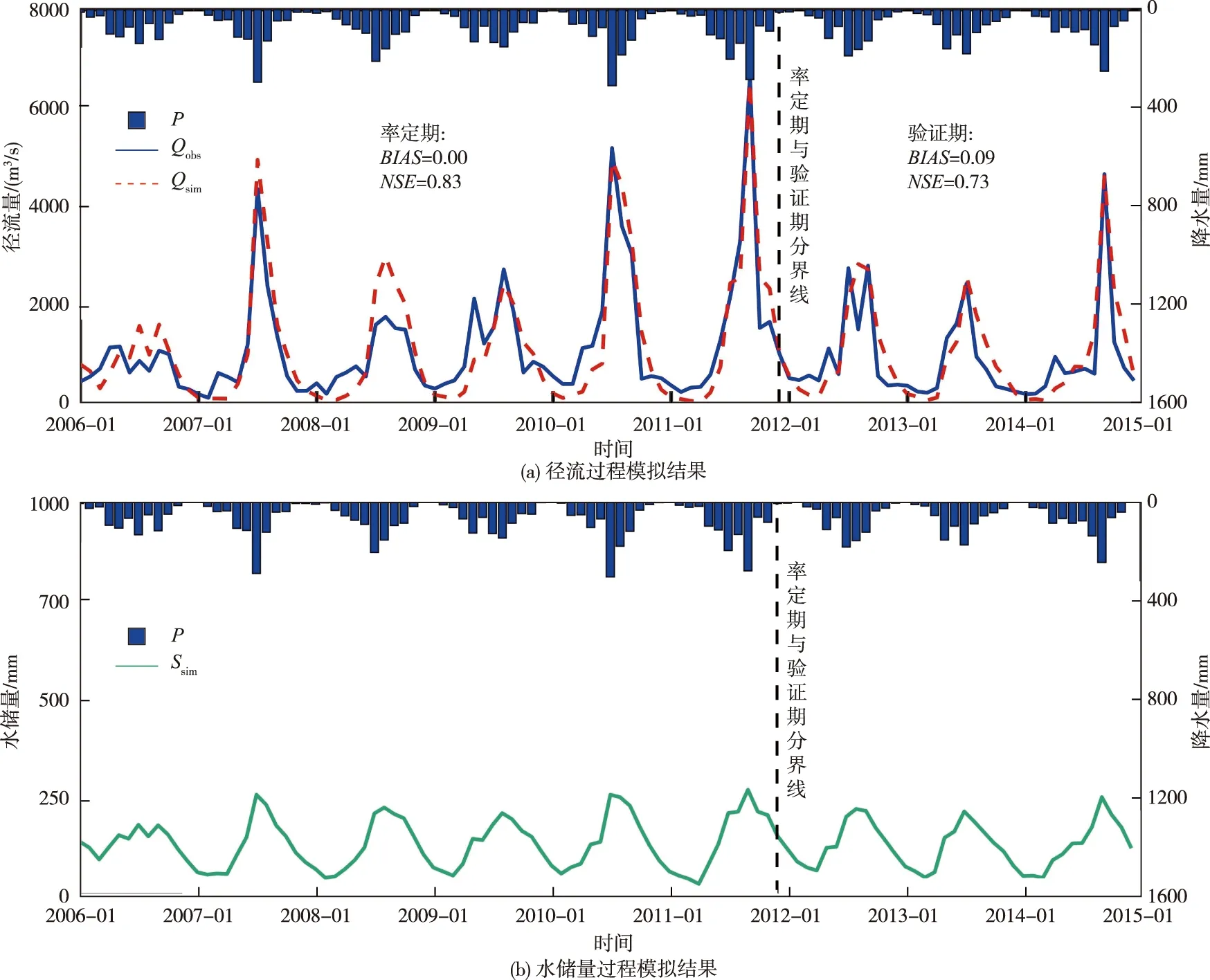
图2 汉江流域上游2006—2014年基于WBM-DP的逐月水文过程模拟结果

图3分别由WBM-DP和GRACE数据得到的2006—2014年汉江流域上游逐月、逐年水储量变化序列。为便于表述，分别以ΔSWBM和ΔSCSR表示。

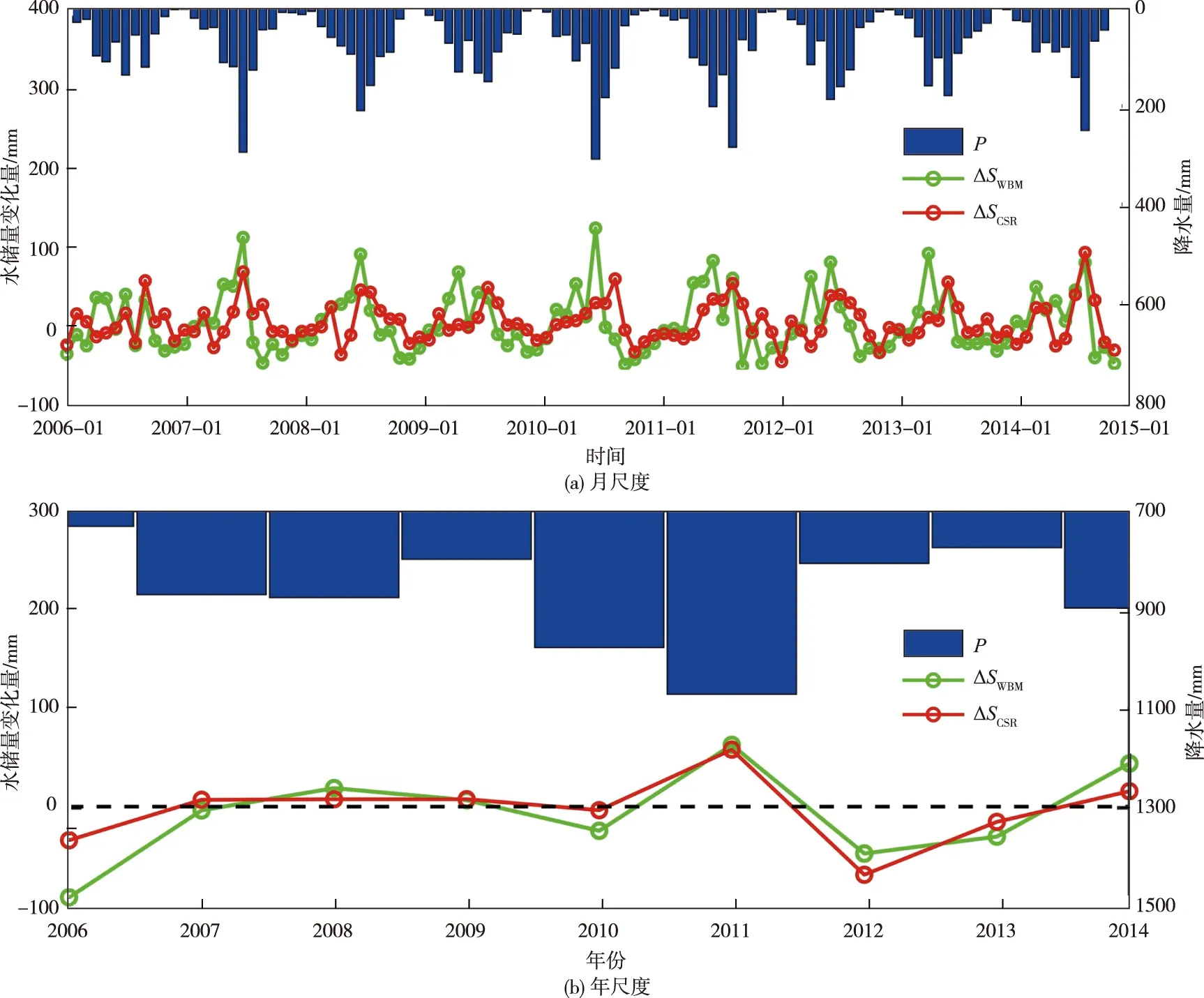
图3 WBM-DP和GRACE数据得到的汉江流域上游2006—2014年月尺度和年尺度流域水储量变化

从图3(a)中可知，在月时间尺度上ΔSWBM和ΔSCSR总体上介于-70～120 mm之间，两者虽具有一定同步性，但对流域面雨量响应特征方面具有明显差异。ΔSWBM较好反映了降水对流域水储量的补给效果，在年内的波动幅度较大；但ΔSCSR存在不少异常情况。如2008年3月以来流域降水量逐步增多，但ΔSCSR不仅未上升反而急剧下降。又2013年流域面平均降水量具有两个明显峰值，ΔSWBM同样表现出2个相对应的水储量变化峰值，而ΔSCSR仅1个。考虑到降水是汉江流域水分主要补给来源，且流域地下水无大规模超采，2004年12月之前南水北调中线工程尚未通水，因此ΔSCSR反映的汉江流域上游水储量过程并不符合对流域水文规律的基本认知。

从图3(b)中可知，年时间尺度上ΔSWBM和ΔSCSR年内水储量变化量总体介于-100～70 mm，两者总体具有较强同步性。但显然ΔSWBM能够更合理的反映出流域降水对水储量的影响，如2006年流域面雨量较2007年和2008年约低200 mm，ΔSWBM反映出流域水储量较2007—2018年偏低100 mm左右，远大于相应ΔSCSR。

可见在汉江流域上游ΔSWBM与流域降水过程的匹配性更好，因此本文倾向于认为WBM-DP对流域水储量变化过程的估计较GRACE更优良。

4.2 蒸散发基准序列差异分别采用ΔSWBM和ΔSCSR构建了汉江流域上游2006—2014年的实际蒸散发基准序列，如图4所示。根据图4(a)，在月尺度上ETGRACE的变化范围在-30～138 mm之间。在每年春、冬两季降水量较小的月份，ETGRACE出现了负值；而在每年5月份前后降水量最大的时段，ETGRACE大幅度超过PET。同时，ETGRACE在年内存在多峰现象，其峰值可能会大幅度高于当月PET。

图4 汉江流域上游2006—2014年基于WBM-DP和GRACE的实际蒸散发基准序列与流域潜在蒸散发对比

ETWBM在月尺度上介于22～67 mm，在年内总体上呈单峰变化，其波动较平缓。由于受水热耦合平衡方程原理限制，ETWBM在所有月份均不会低于零，也不会高于PET。综合图4(a)(b)，总体上ETWBM和ETGRACE的差异在5—7月和9—12月较显著。月尺度上，ETWBM和ETGRACE相差最大可达23.7 mm，相对差异可达到50%以上。在年尺度上两者差异不大。

WBM-DP对径流具有较高模拟精度，构建ETGRACE和ETWBM所采用的月径流量接近，故ETGRACE在月时间尺度上的异常现象主要还是受流域水储量变化ΔSCSR的影响。因此在降水量完全一致、径流量较为接近的情况下，陆地水储量的差异是导致ETGRACE蒸散发基准序列为负值的主要原因。如2011年12月流域面降水量仅8.5 mm，但ΔSCSR并未随着降水量减少而下降，反而进一步升高(2011年11月和12月，ΔSCSR分别为-13.3 mm和10.7 mm)，这导致当月ETGRACE为-29.4 mm；而WBM-DP则能够较合理的给出流域水储量的变化，随着降水量减少，ΔSWBM也呈明显下降(2011年11月和12月，ΔSWBM分别为-8.7 mm和-52.9 mm)，因此当月ETWBM并未出现负值(ETWBM为34.1 mm)。又如2010年7月流域面雨量高达308.1 mm，为当年汛期内最丰，但ΔSCSR并未随降水增多而显著增加(2010年6月和7月，ΔSCSR分别为11.1 mm和24.5 mm)，致使当月ETGRACE达到了111.1 mm，大幅度高于PET(58.0 mm)。虽然在降水供给充足的情况下，流域实际蒸散发有可能超过潜在蒸散发，但前者如此大幅度超过后者，仍然值得注意。而ΔSWBM在2010年7月大幅度增加，但ETWBM低于相应PET。

故总的来说，采用GRACE水储量和水量平衡方程推求流域实际蒸散发，在月尺度上还难以十分准确反映汉江流域上游降水对地下水、土壤、河湖库等空间水储量的补充作用，会导致蒸散发的计算出现异常。

4.3 蒸散发数据精度评估进一步以ETGRACE和ETWBM为基准序列，在汉江流域上游评价了2006—2014年MOD16、Noah、SSEbop 3种蒸散发数据的精度，探究基准序列对遥感或再分析蒸散发数据精度评价结果的影响。

3种实际蒸散发数据对应的2006—2014年汉江流域上游实际蒸散发过程如图5所示。在月时间尺度上，三者具有较强的一致性，与流域降水之间存在明显的正向响应关系。但3种蒸散发数据在主汛期(6—8月)与ETGRACE、ETWBM之间存在明显差异。ETSSEbop相对基准值的高估最明显，ETNoah次之，ETMOD16最低。在年时间尺度上，3种数据较为接近，均明显高于ETGRACE和ETWBM，其原因主要来自于5—9月的高估。

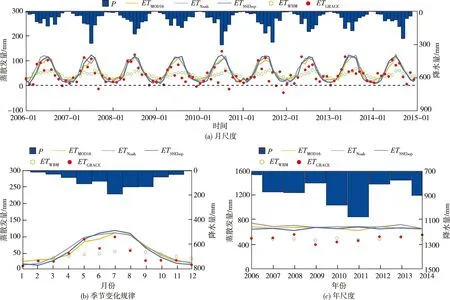
图5 汉江流域上游2006—2014年不同时间尺度下3种流域实际蒸散发序列及2种基准序列变化过程

表2给出了汉江流域上游3种实际蒸散发数据集定量精度评价指标(考虑到数据量较少，年尺度上未计算CC)；图6给出了月时间尺度上的标准化泰勒图(以ETGRACE或ETWBM为基准序列的标准化处理泰勒图，即3种蒸散发数据的标准差及其各自与基准序列的RMSD同时除以基准序列的标准差。标准化泰勒图用于从标准差、均方根误差和相关系数3种指标综合评价多源数据相对基准数据的精度。以图6(a)中的均方根误差指标为例，其坐标轴是图中最大直角扇形的横轴、刻度线是以基准点(ETGRACE)为圆心，标准化后的均方根误差为半径的弧线。图中3种蒸散发数据集介于0.5～1之间，其中MOD16距基准点最近，精度最优。其他2种精度指标的坐标轴分别为最大直角扇形的纵轴和圆弧，精度评价原理近似)。若以ETGRACE作为基准序列，在月时间尺度上3种数据的综合精度较接近。其中MOD16的精度相对最高，其CC略低于SSEbop和Noah，但MAE和CRMSD优于后二者。Noah和SSEbop之间，除RMAE略有差异外，其它3项指标均十分接近。3种数据在汛期各月的综合精度也比较接近，其中MOD16的精度仍最高。但非汛期有所不同，SSEbop的MAE、CRMSD和CC均优于MOD16和Noah，仅RMAE略差，3种数据的综合精度由高到低依次为SSEbop、MOD16和Noah。在年时间尺度上，根据MAE、RMAE和CRMSD3项指标，SSEbop的精度最高，其次为MOD16，Noah最低。

表2 不同时间尺度上2006—2014年汉江流域上游MOD16、Noah和SSEbop精度指标

以ETWBM和ETGRACE作为基准序列，在全年各月、汛期各月以及年尺度上，MOD16、Noah和SSEbop 3种蒸散发数据的综合精度高低顺序一致。但在非汛期各月，如以ETWBM作为基准序列，3种数据的综合精度由高到低依次为MOD16、Noah和SSEbop，而以ETGRACE为基准序列时则依次为SSEbop、MOD16和Noah。更重要的是，综合表2和图6可知，基准序列的不同会导致3种蒸散发数据精度指标的非一致性变化，即有的数据误差减小、有的误差增加，或者虽然误差变化方向一致但变化程度不同。当以ETWBM为基准，相对于以ETGRACE为基准时，对于全年各月(图6(a)(d))，3种数据的CC显著提升，MOD16的误差下降明显，但Noah和SSEbop的误差反而增大，SSEbop增幅最大；对于汛期各月(图6(b)(e))，3种数据的精度指标变差，SSEbop变化最为明显；对于非汛期各月(图6(c)(f))，3种数据的误差全部下降，但Noah和SSEbop的CC上升，MOD16反而下降。可见不同基准序列的选取会使3种数据的定量精度指标发生变化，且三者之间的定量精度差异会更加显著。

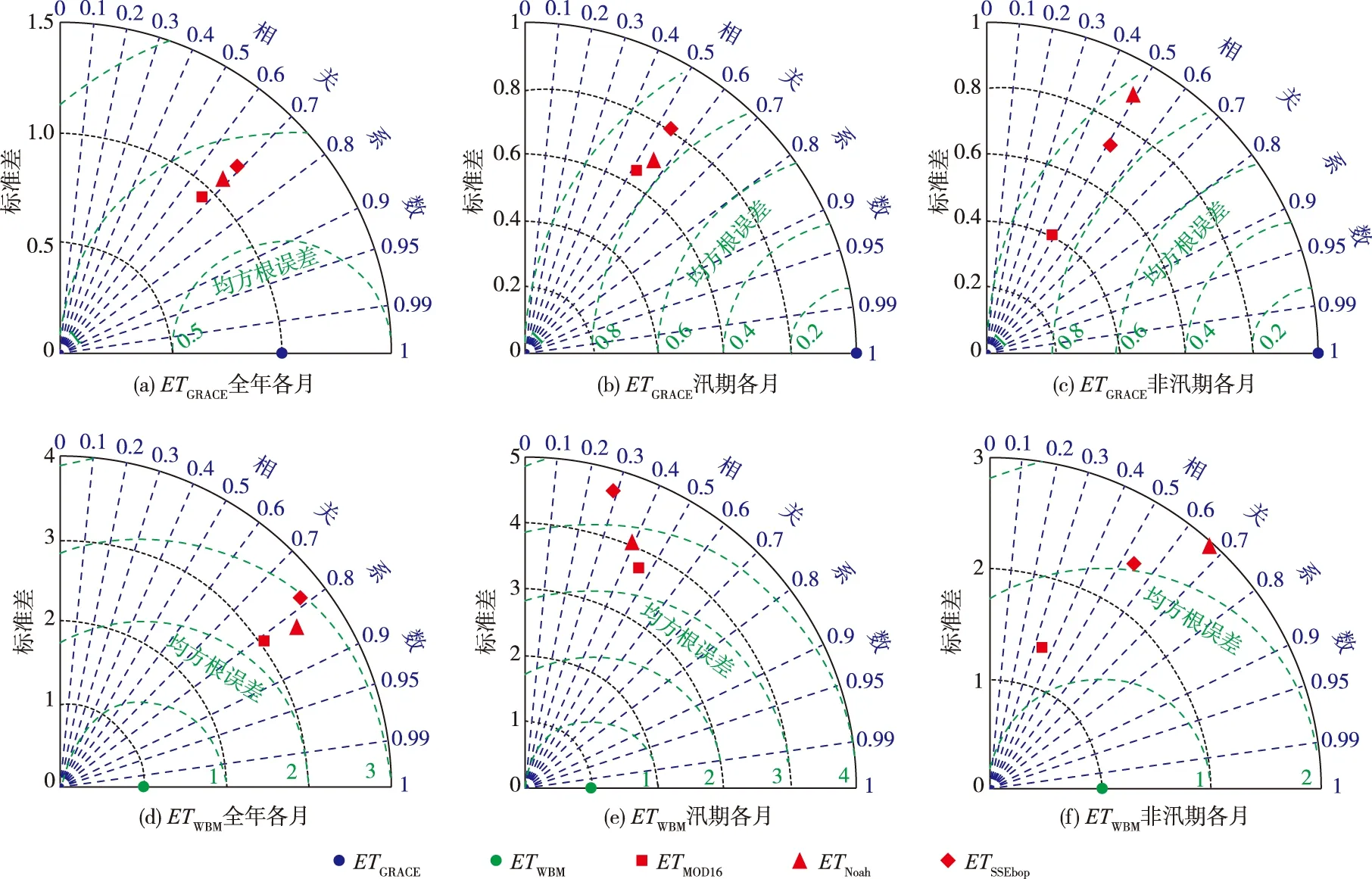
图6 以ETGRACE和ETWBM作为基准序列的3种蒸散发数据精度指标标准化泰勒图

5 结论

本文分别基于GRACE数据和两参数月水量平衡模型WBM-DP构建了2006—2014年汉江流域上游两种蒸散发基准序列ETGRACE和ETWBM，在月和年时间尺度上解析了MOD16、SSEbop和Noah的精度特征，阐明了基准序列不同对卫星遥感反演和再分析蒸散发数据精度评价结果的影响，主要结论如下：

(1)WBM-DP模拟的流域逐月水储量变化序列ΔSWBM较GRACE数据得到的流域逐月水储量变化序列ΔSCSR更为优良，能够更合理反映汉江流域上游水储量过程对降水和潜在蒸散发的响应特征。

(2)在年尺度上，ETGRACE和ETWBM相差不大，但在月尺度上ΔSWBM和ΔSCSR的差异会传导至流域蒸散发基准序列中，ETWBM和ETGRACE在5—7月和9—12月有较明显差异。在某些月份ETGRACE会出现负值或大幅度高于潜在蒸散发的“异常”现象，而ETWBM则无此现象。

(3)在年尺度上，以ETWBM和ETGRACE为基准，得到3种蒸散发数据的精度指标差异不大，但在月尺度上基准序列的不同会导致3种蒸散发数据精度指标的非一致性变化，其精度评估结果也可能不同，相对于ETGRACE，以ETWBM为基准时，不仅MOD16、Noah和SSEbop各自定量精度指标发生了变化，而且三者之间定量精度差异会更加显著。

本文说明，对于卫星遥感或大气再分析蒸散发数据而言，需充分重视基准资料对其精度评价结果的影响。在月时间尺度上，GRACE陆地水储量数据的误差较为突出，以此由水量平衡原理推求流域实际蒸散发时会产生明显的不合理性现象，而流域水量平衡模型则为MOD16等蒸散发数据精度评价提供了另一种可行方法。当然，对于GRACE陆地水储量数据的误差成因，还需要从反演算法和观测周期的时间频次等方面进一步深入分析。同时，需要指出的是，本文仅是汉江流域上游研究的结果，同时所采用的数据序列也不长，相关研究结论还应在其它流域采用更加丰富的资料加以验证和总结。