基于运动试验平台的MOEA/D改进洗出算法仿真及试验
刘伟超,王 辉
(中国民航大学 航空工程学院,天津 300300)
洗出算法是一种在受限于模拟器空间限制的情况下将飞行器产生的力和角速度转化为模拟器运动的驱动算法。经过多年的发展,对于洗出算法的研究逐渐成熟。董彦良等人对经典Washout滤波器进行了设计和分析,实现了良好的洗出效果[1]。同时,许多学者对洗出算法的结构进行了优化:文献[2-3]对增益自适应洗出算法进行了研究。比较成熟的模糊逻辑洗出算法由Asadi等[4-6]提出。文献[7-10]将模糊逻辑等智能控制方法应用到洗出算法,有效改善了相位延迟问题。文献[11-12]对输入信号进行了预处理,避免了平台运动超限。但以上的改进方法计算量较大,运行结果不够稳定,存在实际应用不够广泛的问题。
经典洗出算法结构简单、响应速度快、易于维护,目前经典洗出算法被广泛的应用于商用飞行模拟器中。但是,经典洗出算法参数固定,性能受其参数影响较大,为了提高逼真度可以对其参数进行调整。王小亮等[13]利用遗传算法实现了对经典洗出算法的参数的优化,但采用的是单目标遗传算法,评价指标过于单一,不能够得到综合指标下的最优参数。Asadi等[14-15]在洗出算法参数选择时,将感觉误差以及总的位移量作为评价指标,采用遗传算法以及粒子群算法对参数进行了优化,但目标函数是多个指标的加和的形式,进行单目标优化,并没有进行归一化处理,由于各指标的量纲不同会导致优化结果的不准确,难以实现参数的同步优化。另外,以上大多数对洗出算法的研究均采用仿真的方式验证其有效性,例如罗竹辉等用仿真软件建立并分析了洗出算法的优化模型[11],均缺少实验环境验证洗出的实际效果。
针对以上问题,笔者提出以下方案对洗出算法进行改进优化:
1)针对目前对洗出算法的优化研究均采用仿真的方式验证其有效性,建立了飞行模拟器运动试验平台,将洗出算法数字化处理,利用LabVIEW实现试验平台上位机的设计;
2)不同于目前通常所采用的单目标优化算法对经典洗出进行的优化,提出应考虑人体感知误差、模拟加速度误差和洗出线位移等多个评价指标,采用MOEA/D多目标优化算法,结合模糊隶属度函数对pareto最优解集进行寻优,实现对洗出算法参数的同步优化;
3)以运动试验平台的物理空间为限制条件,对洗出算法的参数进行同步优化,将优化的结果应用于飞行模拟器运动试验平台中,与单目标优化洗出算法以及经典洗出算法进行仿真和试验对比。
1 运动系统试验平台总体设计
飞行员的运动感觉、本体感觉和部分触觉信息可以通过运动平台产生的惯性运动来提供。依据此原理对飞行模拟器运动试验平台进行了设计。飞行模拟器运动试验平台是以Stewart机构为运动平台,由上位机位姿的实时解算和下位机实时输出位姿提供运动感觉2部分组成(图1)。工作原理为:首先通过飞行驾驶员的操纵获取飞机在体坐标系下的运动参数,经过坐标转换得到惯性坐标系的飞机姿态信号,由改进洗出算法运算得出运动平台的实时位姿信号,然后将运动平台的位姿进行实时运动学反解,最后将信号输入到运动平台中驱动平台运动,从而使飞行驾驶员产生动感。

图1 飞行模拟器运动试验平台工作流程
运动试验平台的硬件组成主要有Stewart平台、伺服电动缸、伺服驱动器、运动控制卡、串口数据线和计算机等,如图2所示。其中上位机与下位机采用RS-232异步串行的通讯方式,波特率为115 200 bit/s;起始位:1位;数据位:8位;停止位:1位;奇偶校验:无。运动试验平台主要工作参数如表1所示。

图2 运动试验平台硬件

表1 运动试验平台主要工作参数
2 洗出算法MOEA/D多目标优化
为了改善经典洗出算法参数调整较为复杂以及通常采用试错方法的弊端,采用基于分解的多目标优化方法,对经典洗出算法的重要参数进行同步优化,使洗出效果达到最优。
2.1 洗出算法与人体感知模型
2.1.1 洗出算法
经典洗出算法(图3)主要由比例环节(SCALE)、坐标转换矩阵(LIS、TIS)、高通滤波环节、低通滤波环节、倾斜协调模块(TILT COORD)、角速度限幅模块(RATE LIMIT)等组成。输入信号为机体坐标系飞机的线加速度aAA=[aAAxaAAyaAAz]T和角速度ωAA=[ωAAxωAAyωAAz]T,输出信号为动平台质心的位置矢量s=[sxsysz]T和空间角矢量β=[βxβyβz]T。经典洗出算法3个通道为:加速度高通通道、倾斜协调通道、角速度高通通道。
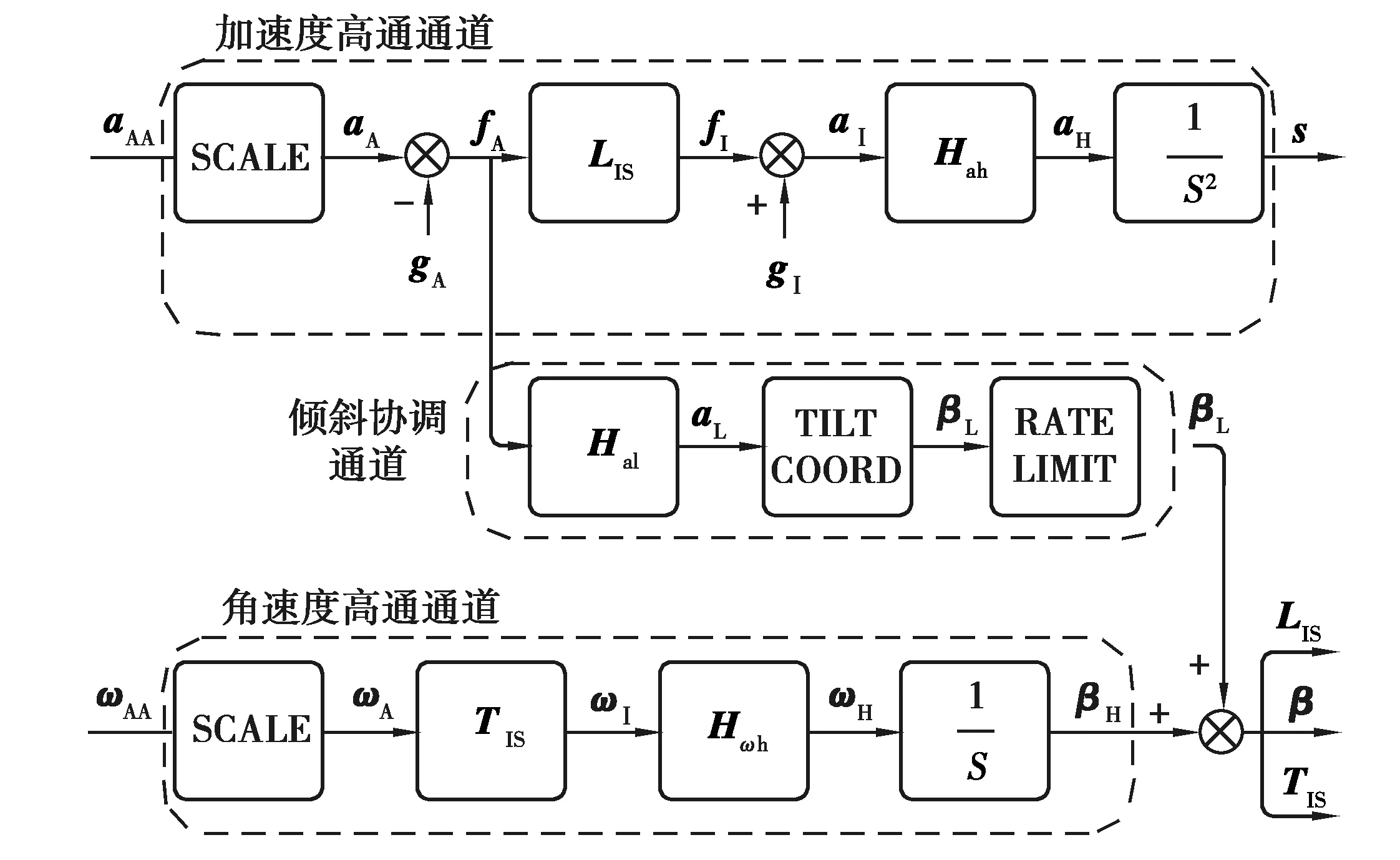
图3 洗出算法流程
其中,加速度高通滤波器的一般形式为
(1)
式中:ωm为一阶截止频率,ωah为加速度高通滤波器截止频率,ξah为滤波器阻尼比。
倾斜协调通道中的低通滤波器的一般形式为
(2)
式中:ωal为加速度低通滤波器截止频率,ξal为加速度低通滤波器阻尼比。
角速度高通滤波器的一般形式为
(3)
式中:ωωh为角速度高通滤波器截止频率,ξωh为角速度高通滤波器阻尼比。
2.1.2 人体感知模型
人体前庭系统中半规管可以感知旋转运动,耳石能够感知到比力f,即外力下的加速度a与重力加速度g的矢量和[16]。
耳石模型传递函数为
(4)
式中:k为常系数,τA、τL、τS为耳石模型的相关系数。
半规管模型的传递函数为
(5)
式中:TL、TS、TA为半规管模型的相关系数。
2.2 MOEA/D多目标优化算法
基于分解的多目标算法MOEA/D将一个多目标优化问题分解为若干个标量优化子问题,并同时对它们进行优化。由于分解操作的存在,该方法在保持解的分布性方面有着很大优势。通过分析相邻问题的信息来优化,能在避免陷入局部最优的同时使计算简单(图4)。

图4 MOEA/D多目标优化算法流程
首先进行初始化。初始化操作包括:初始种群大小N、初始种群Population以及种群对应的目标函数值数组F、目标函数数目M,均匀分布的权重向量数组λ、每1个权重向量的邻居个数T、生成邻居索引数组B、精英种群E。然后取F中的最优值组成初始全局最优数组z,在数组B中随机选取2个邻居序号进行种群索引,经过子代变异和多项式变异后得到新个体y。之后进行评价与更新,其内容包括:1)更新全局最优数组z;2)采用切比雪夫聚合方法更新相邻解;3)更新精英种群E。最后判断终止条件。MOEA/D多目标优化算法的最终输出为用于保存pareto最优解的精英种群E。
2.3 目标函数
将人体感觉误差作为优化模型的主要目标。同时,为了节省运动平台的工作空间,将平台的位移与旋转角度作为洗出算法优化的评价标准之一。根据经验可知,过于节省平台的工作空间也会出现模拟加速度误差的变化差异过大的现象。这里以纵向(x方向)加速度高通通道和倾斜协调通道为例,对加速度高通滤波器截止频率ωahx和加速度低通滤波器截止频率ωalx寻优的过程加以介绍,角速度高通滤波器的截止频率的优化过程类似,就不再赘述。
为了综合评价洗出算法的性能,选取3个性能指标:人体感知误差eef、模拟加速度误差ef和洗出线位移x,如图5所示。其函数表达式如下所示。
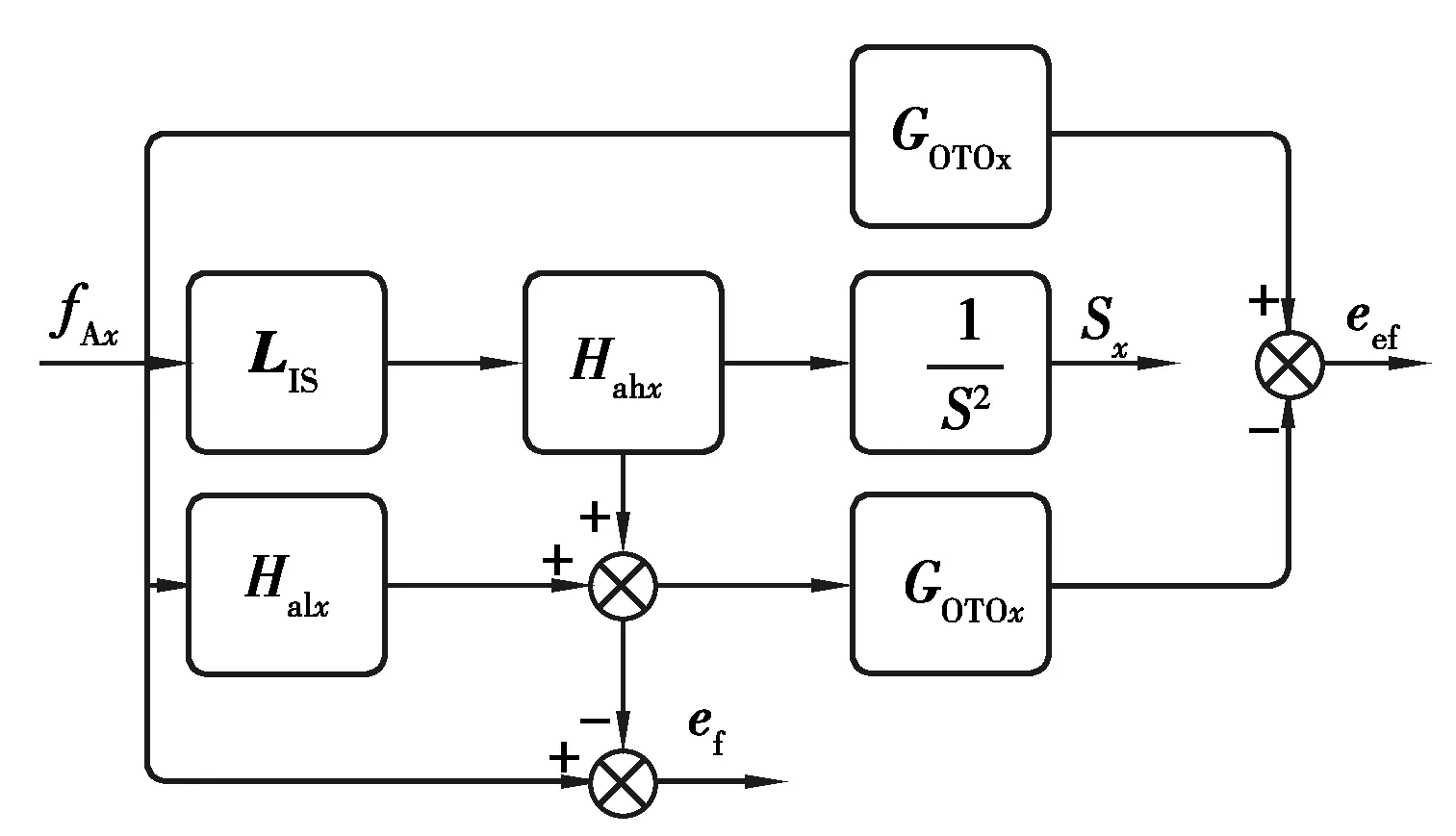
图5 评价指标原理图
L[eef]=GOTOx(L[fAx](1-Halx)-L[fAxLIS]Hahx),
(6)
L[ef]=L[fAx](1-LISHahx-Halx)
(7)
(8)
式中:L为拉普拉斯变换。fAx为纵向比力。
目标函数如下所示
(9)
式中std代表标准差的计算。
2.4 多目标同步优化
进行优化前,对初始参数进行赋值。设输入的纵向(x方向)比力fAx为1~5 s时间内值是1的方波信号,总时长t为10。设置MOEAD多目标优化算法初始参数值:算法种群大小N=105;最大迭代次数G=700;邻域大小T=10。
变量设置为
X=[x1x2x3x4x5]=[ωahxωmxωalxξahxξalx],
(10)
则目标函数为
(11)
约束条件设置:为了满足平台运动空间的要求,洗出线位移x∈[-0.17,0.17];设置ωmx=1、ξahx=1、ξalx=1,将ωahx、ωalx作为待优化变量,且为了保证平台在规定时间内完成动作,需要满足ωahx∈[1.5,4]、ωalx∈[1,4]。
寻优过程是将人体感知误差f1、模拟加速度误差f2和位移行程f3三个相互制约的指标作为优化目标,不断修正最优前端面,最终得到pareto最优解集(图6)。
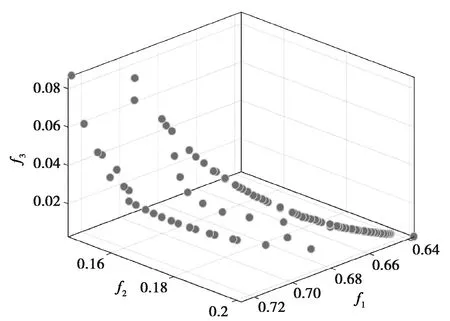
图6 Pareto最优解集
2.5 模糊隶属度函数
获得Pareto解集后引入模糊隶属度函数表示各个目标的满意度。模糊隶属度函数的定义如下
(12)

对于每个解,用式(13)求其标准化满意值
(13)
式中μi为第i个解的标准化满意值。标准化满意值最大的解就是最优折中解。
2.6 仿真与分析
通过优化算法得出的最优截止频率的值为:ωahx=3.5 rad/s,ωalx=3.46 rad/s。与文献[17]中采用单目标优化算法的洗出算法以及文献[1]中应用经典洗出算法进行对比分析。
以纵向模式进行仿真,设置输入加速度为在2 s时变为0.5 m/s2的阶跃信号。输入角速度在仿真时间内设置为0,仿真时间为10 s。仿真结果如图7~11所示。
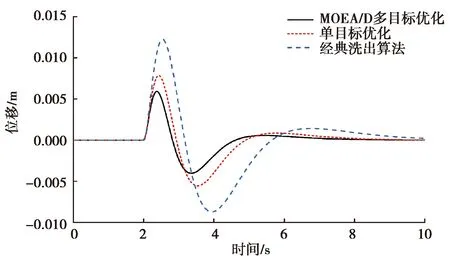
图7 洗出位移曲线
在采用不同方法对洗出算法进行优化时,其具体的参数对比如表2所示。由图7可知,在模拟同一加速度信号时采用MOEA/D优化后的洗出算法所需的位移量最小,且能够更快速的回到初始位置,准备下一次的动作。另外由图8可知,MOEA/D优化后的洗出算法高通加速度曲线的稳定时间更短,相比于单目标优化洗出和经典洗出,稳定性分别提升了20%和30%。
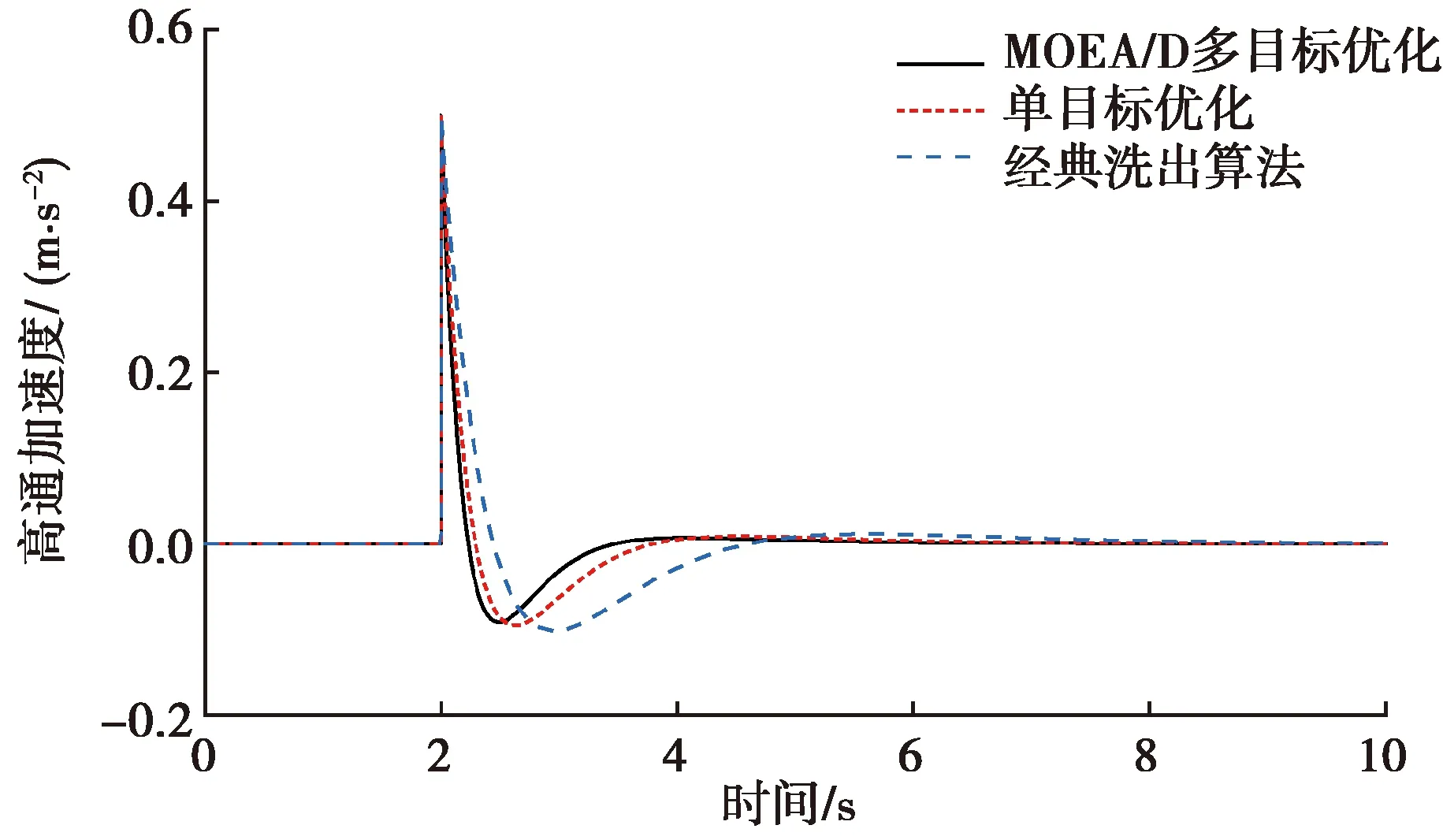
图8 高通加速度曲线

表2 采用不同方法优化洗出算法性能比较
由图9可知,MOEA/D优化洗出算法的感觉峰值延迟,相比于单目标优化洗出和经典洗出分别减少了0.9 s和2.4 s,且消除了感觉峰值误差。由图10可以得出,2种优化算法将误差峰值从0.5 m/s2分别降低到了0.42 m/s2和0.39 m/s2,比力误差均方根由0.26 m/s2分别降到了0.190 5 m/s2和0.163 1 m/s2,同时误差稳定时间也得到了缩减。
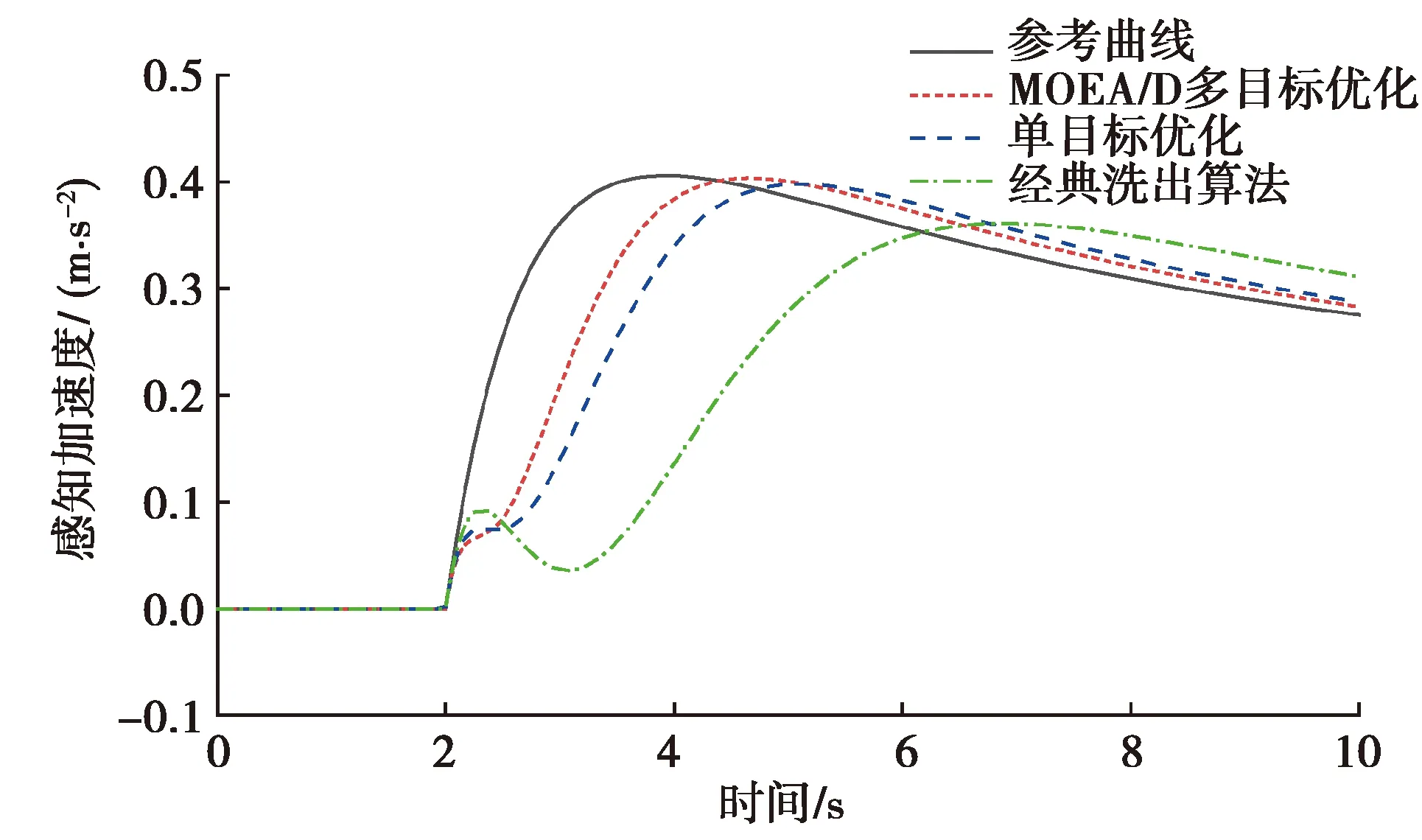
图9 感知加速度曲线
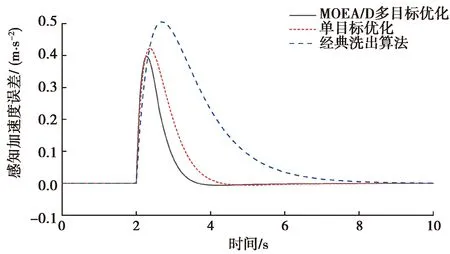
图10 感知加速度误差曲线
由图11表明MOEA/D优化洗出算法在没有产生错误暗示的前提下倾斜协调反应更加迅速。由图12可知,三者均未超过人体角速度感知阈值0.062 8 rad/s,不会产生错误暗示。
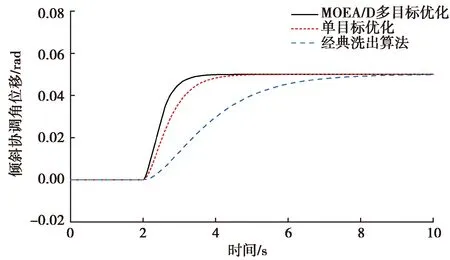
图11 倾斜协调角位移曲线
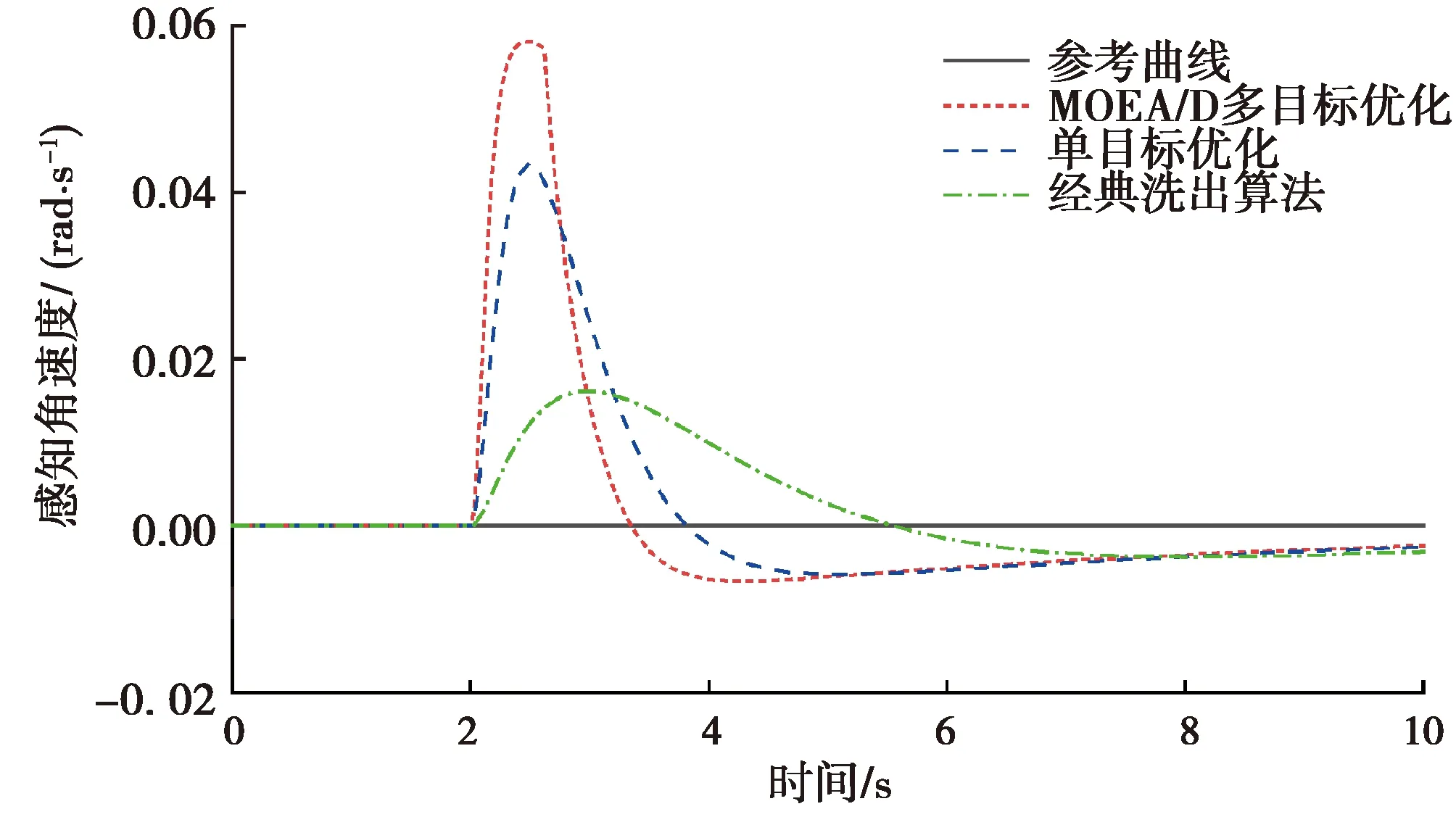
图12 感知角速度
3 模拟器运动试验平台上位机设计
3.1 洗出算法数值化实现
在计算机上数值化实现MOEA/D改进洗出算法的重点是将改进洗出算法中高、低通滤波器的传递函数转化成差分方程的形式。采用双线性变换方法,将传递函数转换为Z变换形式,再根据Z变换推导出差分方程表达式,从而得到相应的实际输出信号。整体的方式流程如图13所示。

图13 数值化流程
以纵向加速度低通滤波器的数值化方法为例,其他滤波器数值化方法类似,不再赘述。洗出算法加速度低通滤波器通常采用二阶低通滤波器
(14)
通过双线性变换进行离散化处理,其公式为
(15)
得到离散域的传递函数为
(16)
经过差分变换可以得到差分方程
(17)
上式中的参数取值为
以上则完成了对洗出算法中低通滤波器的数值化。
3.2 LabVIEW平台洗出算法实现
洗出算法的3个滤波通道需要并行计算。利用LabVIEW平台的并行化处理机制,将洗出算法的3个滤波通道进行数值化实现。基于LabVIEW的上位机系统程序框架如图14所示。将解算出来的位姿数据通过LabVIEW中的VISA写入模块以串口通讯的方式发送给下位机平台,使六自由度平台执行相应的位姿指令。同时下位机平台实时反馈运动平台的运动状况,达到监控的目的。

图14 上位机系统程序框架
上位机系统的输入量主要包括:1)系统采样时间T(可调节全局变量);2)加速度比例环节Ga、角速度比例环节Gω(均为可调节全局变量);3)加速度高通滤波器截止频率ωah、加速度低通滤波器截止频率ωal、角速度高通滤波器截止频率ωωh(均为可调节全局变量);4)t=kT时刻的加速度αAA(k)、角速度ωAA(k)(初值为0);5)t=(k-1)T时刻角位移信号β(k-1)。
上位机系统输出量主要包括:t=kT时刻的线位移信号s(k)、角位移信号β(k)。经过浮点数十六进制编码,通过串口通讯的方式输出到下位机运动平台。
系统从输入到输出之间的变换策略主要包括:加速度高通通道比例环节的增益策略、坐标转换方法、积分策略、倾斜协调策略以及角速度限幅方法等。下面以纵向(x方向)倾斜协调通道中的策略与方法为例,进行推导。
输入加速度信号首先经过增益策略(式(24)),然后经过低通数字滤波器(式(17)),再经过倾斜协调策略(式(25)),最后通过角速度限幅方法输出限制过的角位移。其中角速度限幅方法包括对倾斜角度求导(式(26))、角速度限幅(式(27))、Trapezoid Rule数值积分(式(28))。
aAx(k)=GaxaAAx(k),
(24)
βLx(k)=-arcsin(aLx(k)×9.8),
(25)
(26)
(27)
(28)
以上即完成了对倾斜协调通道的数值化实现,其他通道同理。在程序设计的过程中的重要参数变量,如截止频率ωah、ωal、ωωh和采样时间T以及比例环节Ga、Gω等,均为全局变量,可作为对洗出算法进行优化改进的重要参数接口。通过优化这些重要参数可以实现将上位机系统灵活应用于不同规格的模拟器。
4 试验与分析
4.1 试验过程
试验应用基于LabVIEW的飞行模拟器运动试验平台上位机系统程序对运动试验平台的实际运行情况和改进洗出算法在运动试验平台上的洗出效果进行验证。下位机的运动平台采用ACE6-75-200六自由度平台(图15)。运动试验平台上位机产生实时位姿信号,通过RS-232异步串行通讯将实时位姿信号发送到下位机中,使六自由度平台复现运动信号的动感效果。同时,下位机实时回传6个私服电缸的杆长数据实现实时监控。

图15 六自由度运动平台
选用一段噪声信号来模拟飞机的纵向加速度信号,输入到上位机系统程序中进行试验分析。输入纵向加速度信号(图16)持续时长10 s,角速度信号输入为0。当输入的纵向加速度信号经上位机系统中的高通数字滤波器和低通数字滤波器处理之后,能够分别得到加速度高通信号和加速度低通信号。为了分析洗出效果,三者的信号对比如图17所示。同时,运动试验平台系统能够实时计算出相对应的线位移信号和角位移信号如图18、19所示。当输入信号为图15时,六自由度运动试验平台实时的各个杆长数据如图20所示。以1、4杆的杆长变化情况作为对比,在输入相同的纵向加速度信号的条件下,比较分别采用MOEA/D多目标优化洗出算法、单目标优化洗出算法和经典洗出算法时,飞行模拟器运动试验平台杆长的实时变化情况,如图21所示。
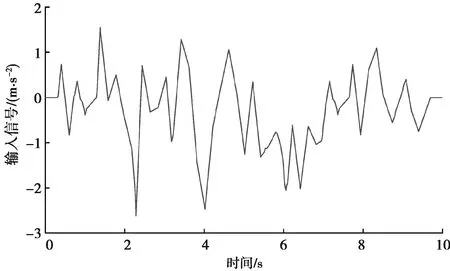
图16 输入信号
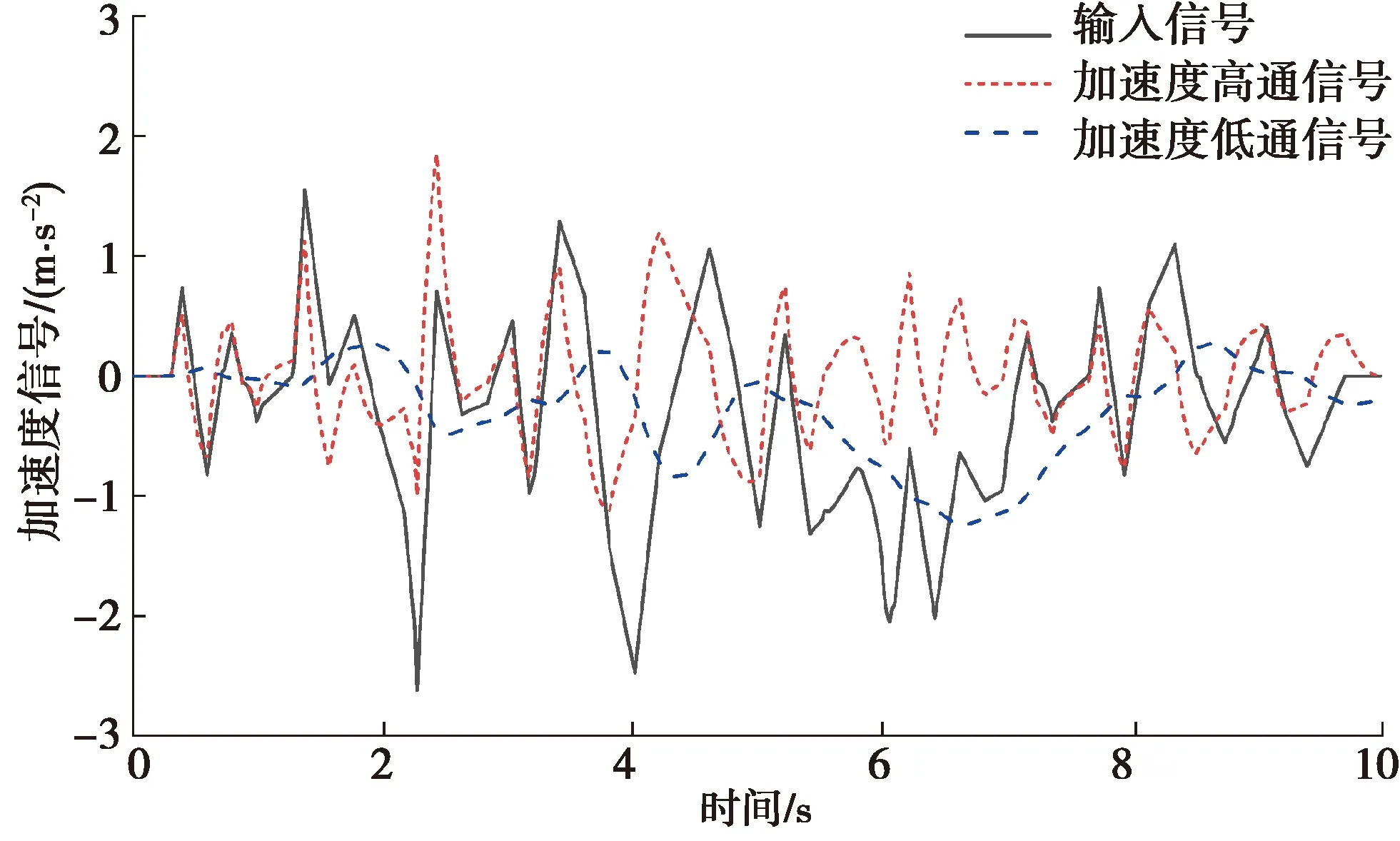
图17 信号对比曲线
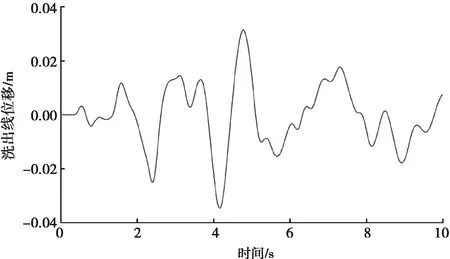
图18 线位移信号
图19 角位移信号
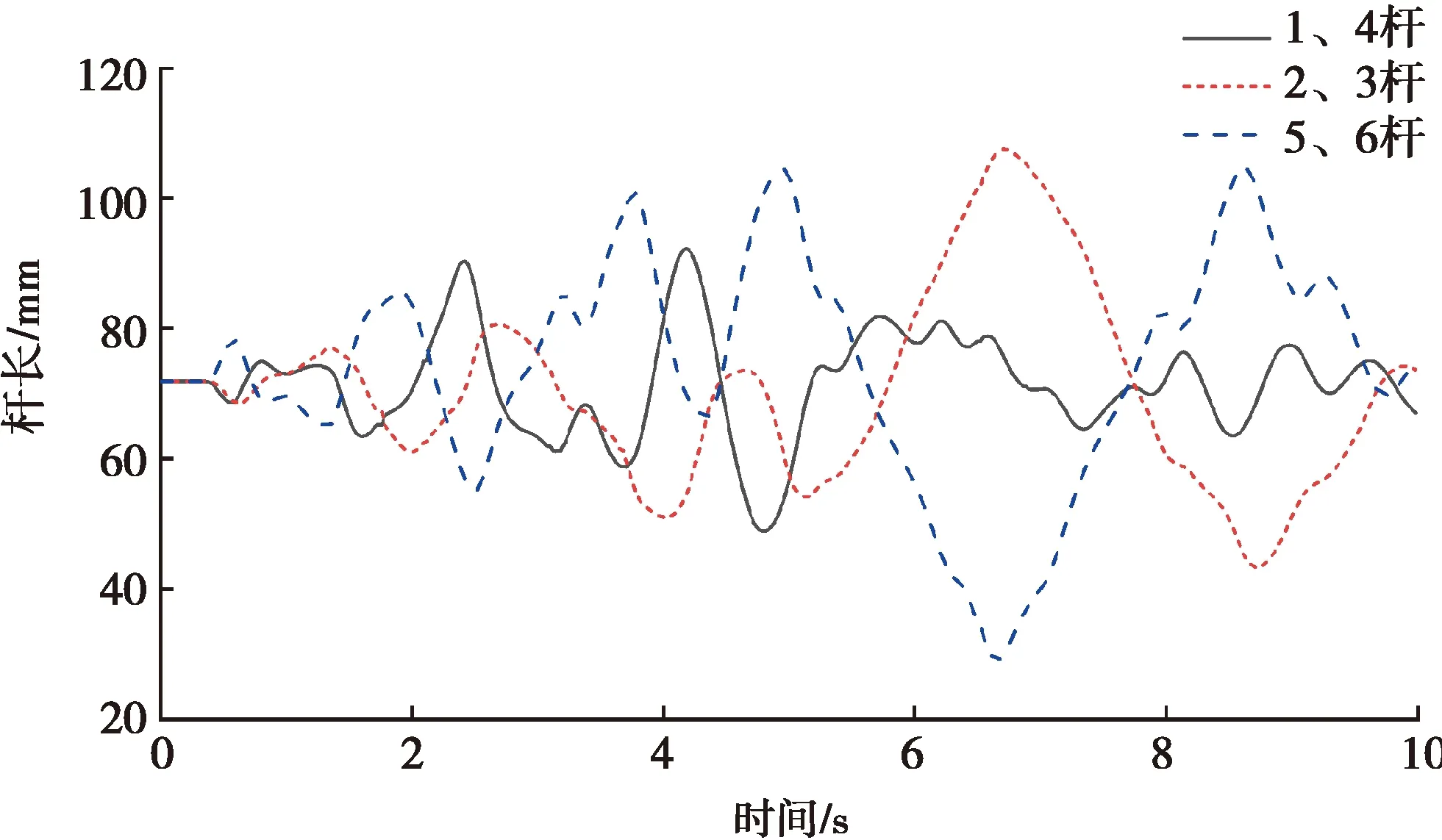
图20 杆长数据
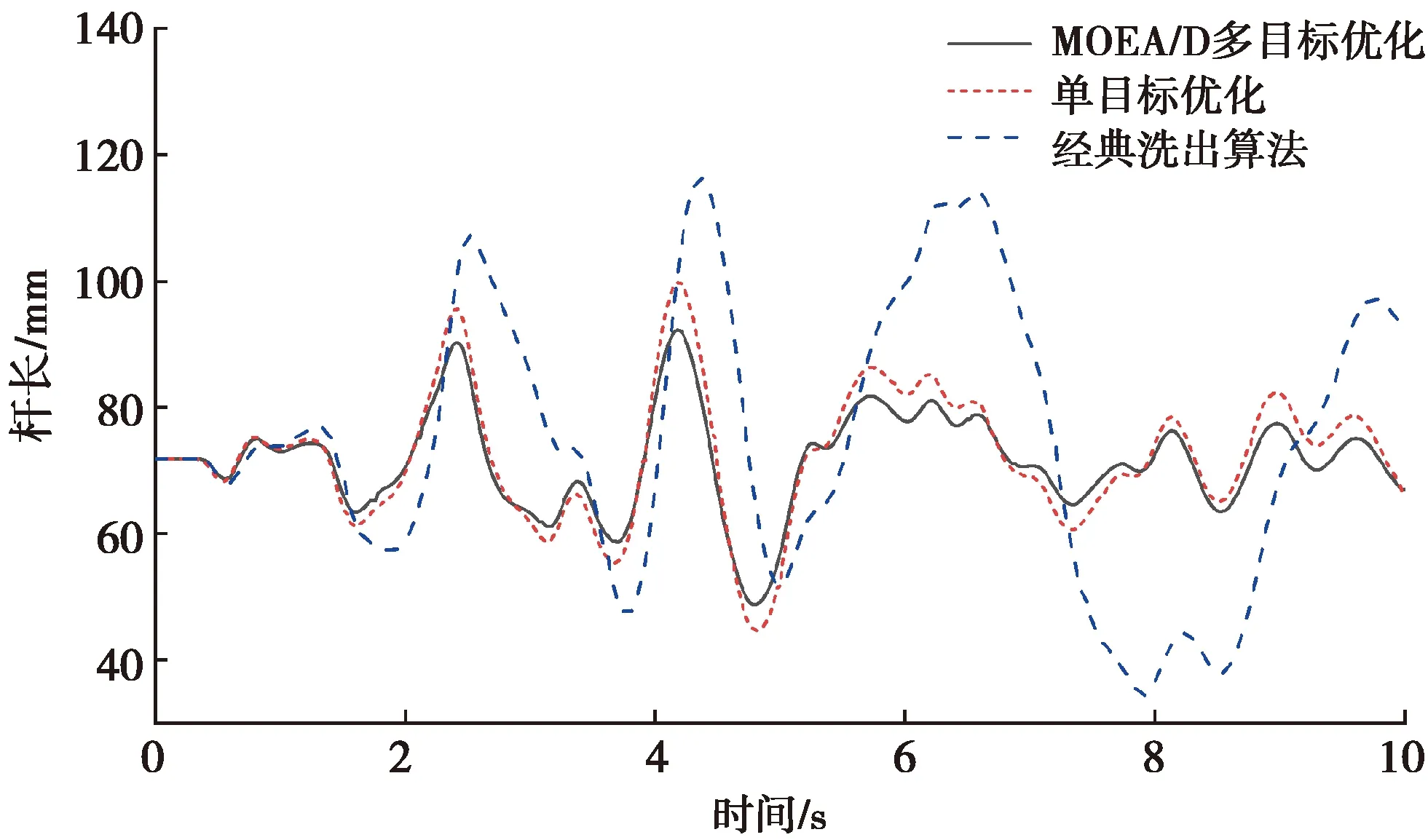
图21 1、4杆长对比曲线
4.2 试验结果分析
由图17中输入信号与滤波后的信号比较可见,通过滤波将飞机的加速度信号分为高频和低频信号,其中低频信号从宏观上跟随着输入信号的变化,该频段信号将转换为平台的倾斜动作(图19)。高频信号则表达出了输入信号变化的高频部分,且该频段信号将转化为平台的平移动作(图18)。高频信号与低频信号的和,可以近似的表达出原始输入信号。表明飞行模拟器运动试验平台实际运行的洗出过程合理、有效。
1、4杆的初始杆长为71.8 mm,由图21可知,基于MOEA/D多目标优化洗出算法得出的杆长曲线最接近于其初始杆长,其极限杆长为92 mm;相比于MOEA/D多目标优化洗出算法,单目标优化洗出算法得出的杆长曲线在杆长变化的高频部分与初始杆长偏离的更大,其极限杆长为98 mm。经典洗出算法得出的杆长曲线与初始杆长偏离最大,其极限杆长为116.3 mm;这意味着,基于MOEA/D多目标优化洗出算法相比于单目标优化洗出算法和经典洗出算法,在提供更加逼真的动感的同时,分别节省了22.9%、54.6%的平台工作空间。
5 结 论
1)对于大多数洗出算法的研究均缺少实验环境验证其洗出的实际效果,笔者对飞行模拟器运动试验平台进行了设计与开发,并将优化后的洗出算法应用于试验平台中。利用数值化方法,在LabVIEW平台上对运动试验平台系统进行搭建,并且预留了对洗出算法进行优化改进的重要参数接口,具有可移植性,经试验证明洗出效果良好。
2)针对飞行模拟器洗出算法采用的不同方案,仿真结果表明MOEA/D多目标优化洗出算法相比于单目标优化算法和经典洗出算法归位时间更短,感觉幅值更加贴近参考值,感觉相位延迟分别减少1.5 s和3.5 s,稳定性分别提升12.5%和30%。试验结果表明,改进算法增加了模拟逼真度的同时,优化了54.6%的平台工作空间。MOEA/D改进洗出算法可以使飞行模拟器在模拟极限运动时有更充足的运动空间并且能够产生更逼真的动感。详细叙述了运动平台中洗出算法的应用过程,未来无论是对于洗出算法的优化研究还是在运动平台开发方面,均可以在此基础上进行研究。

