基于静压变化的隧道风管漏风计算方法

曾艳华，姚文浩，田啸宇，范 磊，刘 祥

（1.西南交通大学 交通隧道工程教育部重点实验室，四川 成都 610031；2.中铁二院工程集团有限责任公司，四川 成都 610031）

在隧道施工中，通常采用风管向施工工作面提供新鲜空气，并排出有害气体和粉尘。随着通风距离增长，风管普遍存在较严重的漏风现象，漏风会减少最终抵达掌子面的新鲜风量，使供风效率降低，最终不仅会降低生产效率，还会影响施工人员的健康，严重时甚至危及生命。合理地计算特定工况下的风管漏风量，有助于调整风机的选型和参数，是长隧道风管通风效果好坏的关键因素之一。

早期关于隧道风管漏风计算的理论有［1］：平均百米漏风率计算理论、日本高木英夫计算理论、沃洛宁计算理论及日本青函隧道计算理论。这些计算理论都是建立在假设管路的百米漏风率为1个定值的基础上，没有充分考虑到风管内静压及风量的沿程变化对风管漏风率的影响。

近年来国内外在风管漏风率方面也进行了许多研究：Auld［2］引入了“管道效率”概念，量化了泄漏对通风管道性能的影响，并分析了风管泄露量对各种参数变化的敏感性；Jo 等［3］针对超长海底隧道，改良了风管的接头材料和接头结构，发明了一种新型风管连接方法，可有效减小风管漏风率；Ma 等［4］和Wos 等［5］在风管漏风率的测试方法上进行了大量测试研究，简化了阻尼筛和流量孔板，得到了一种简便的风管漏风量测量方法，并通过实例证明了其准确性和可操作性；李琦等［6］通过理论推导结合现场实测的方法研究了高海拔隧道的漏风情况，对高海拔情况下的风管漏风率修正系数进行了研究；王晓莉等［7］通过理论分析得出了风机串联时避免风管产生循环漏风的风机间隔距离计算式；谭信荣等［8］通过对兰渝铁路高瓦斯隧道的现场测试，发现风管漏风率对通风效果的影响仅次于隧道断面大小；李科祥等［9］和高红军等［10］通过现场布置测点实测的方法发现风管的百米漏风率在前500 m 段百米漏风率可达到8.37%，并提出了一系列减小风管漏风率的措施。前述研究主要集中在漏风量测量、漏风率减小方案及风管结构优化上，对隧道施工通风中风管漏风率的计算理论研究较少。

本文采用试验测试和理论分析，进行了漏风率随风管静压变化规律研究，在此基础上，基于达西阻力公式推导了长距离风管的总漏风率分段迭代算法；并分析了通风距离、风管直径和海拔高度对长距离压入式通风总漏风率的影响，为施工通风设计提供了参考。

1 漏风率测试

风管的漏风控制质量同风量和风压一样，都是通风设计的重要组成部分［11］。在压入式通风系统中，风管漏风率是指在系统工作压力下，单位时间内风管漏风量与风机出口风量的百分比。在JGJ/T 141—2017《通风管道技术规程》［12］中认为风管漏风量的测试应采用风管内静压进行相关计算，其最大漏风量限定值与检测静压限定值的关系为

式中：[q]为最大漏风量限定值，m3·h-1· m-2；p为风管内承受的检测静压，Pa；k为关于漏风检测的系数，分5个等级。

式（1）表明，风管漏风量和风管内的静压紧密相关。目前风管漏风率测试中风管的工作静压一般取500～2 000 Pa之间，2 000 Pa即视作高压，而在实际工程中，隧道施工通风的风管内最大静压常常可达5 000 Pa以上。本节旨在通过不同静压下的风管漏风率测试研究，找出百米漏风率随管内静压的变化关系，并对测试结果进行线性拟合，得到基于静压变化的风管百米漏风率计算式。

1.1 试验原理及方案

参照GB/T 15335—2019《风筒漏风率和风阻的测定方法》［13］，在中煤科工集团重庆研究院采用几何比例1∶1 的隧道通风模型进行模型试验。试验装置示意图及现场布置如图1所示。图中：风量采用文丘里管测量，静压采用测压计测量；风量测点A和风量测点B所测数据相加可得风机供风量Qf；风量测点C和风量测点D所测数据相加可得出口端风量Qe；静压测点①和静压测点②分别测量风筒始端静压H1和末端静压H2。

图1 试验装置示意图及现场测试

试验的计算原理为

式中：β为百米漏风率；H为风管平均静压，Pa。

试验风管类型采用塑料涂覆布正压风管，参数见表1。

表1 试验基本条件

在入口端两侧并联设置风机，限于试验环境和试验条件，每侧均由3台小型风机串联组成。通过改变工作风机的级数和频率来改变风管内的静压，设置17个工况，试验工况下风机参数见表2。每个工况点都进行3次试验，以确保结果的正确性。

表2 试验工况下风机参数 Hz

1.2 测试结果

采用自动采集系统将数据集成到计算机上，试验所得结果见表3。表中：百米漏风量和百米漏风率均为3次平行试验的平均值。

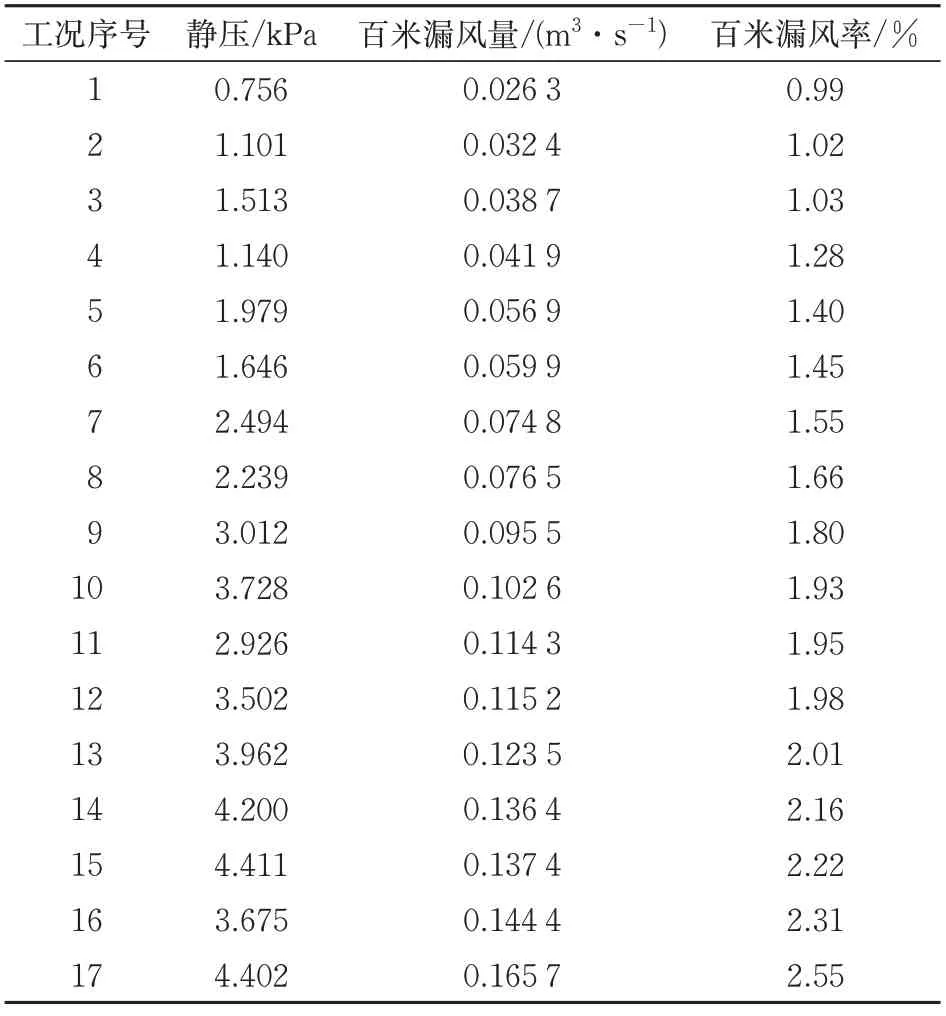
表3 漏风率测试结果

3组平行试验的误差棒分析结果如图2所示。采用均值绘制的“漏风率-静压”散点图及其线性拟合关系如图3所示。

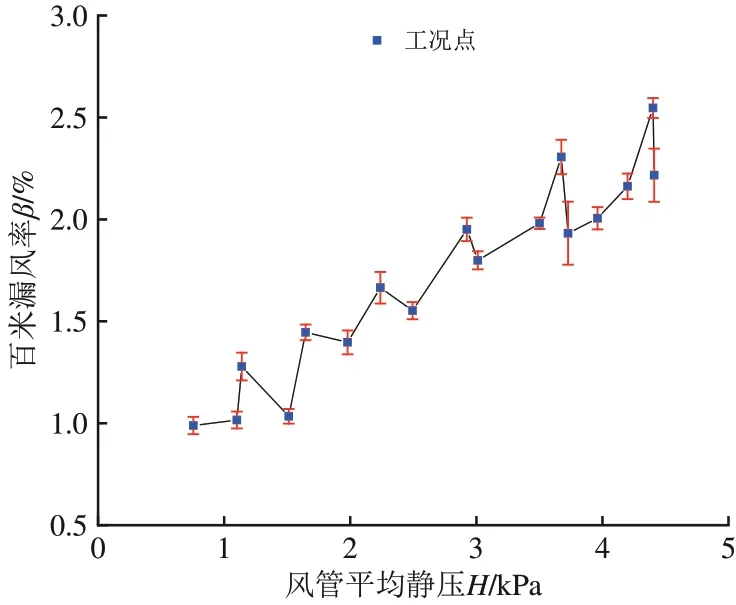
图2 3组平行试验的误差棒分析结果

由表3 和图3 可知：整个测试各工况下风管的静压在0.5～4.5 kPa 之间，百米漏风率维持在1.0%～2.5%水平。且随着管内静压不断增加，风管的百米漏风率也随之增大，管内静压与风管百米漏风率有明显的正相关关系。

图3 百米漏风率与静压的拟合关系

进行线性拟合后得到的关系式为

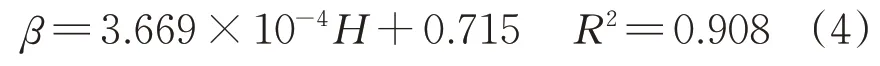
决定系数R2=0.908，表明拟合度较好。由此得到了在一定条件下隧道风管基于静压变化的百米漏风率计算式。本试验的风管各段采用拉链接头连接，实际观察中发现风管管身几乎没有破损，风流主要从接头处泄露，因此在实际应用时，如若实际工程中风管有明显破损，可结合现场实测数据适当增加式（4）的截距。

2 总漏风率的计算方法

在压入式通风中，风管内的静压分布受风机出口静压和管壁摩擦阻力影响，而摩擦阻力与管内流动风量和风管直径相关，管内流动风量又受风机出口风量和漏风量控制，因此，风管内的静压分布由风机出口静压、风机出口风量、漏风量和风管直径决定。风管的漏风量影响静压分布，静压分布又影响漏风量的大小，二者的相互影响会随着通风距离的变化而变化。在实际工程中，隧道独头施工的通风距离往往会超过千米，甚至达数千米，如果直接对整段风管漏风量取平均静压进行计算，将引起较大误差。因此，采用第1节中对静压与漏风率的测试拟合式（4），结合分段迭代计算的方法，推导出更可靠的总漏风率计算式。

2.1 分段迭代计算法

分段迭代计算法计算时，首先将风管分为N段，每段长100 m，其中单元段的序号从出口处至入口处依次递增。

式中：L为通风距离，m。

分段迭代计算法示意图如图4所示。图中：qi为单元段漏风量，m³·s-1，i=1，2，…，N；Hi为单元段的平均静压，Pa；Q0和Qi为截面风量，m3·s-1，其中Q0为出口截面风量，也就是掌子面需风量，QN为入口截面风量，也就是风机供风量。

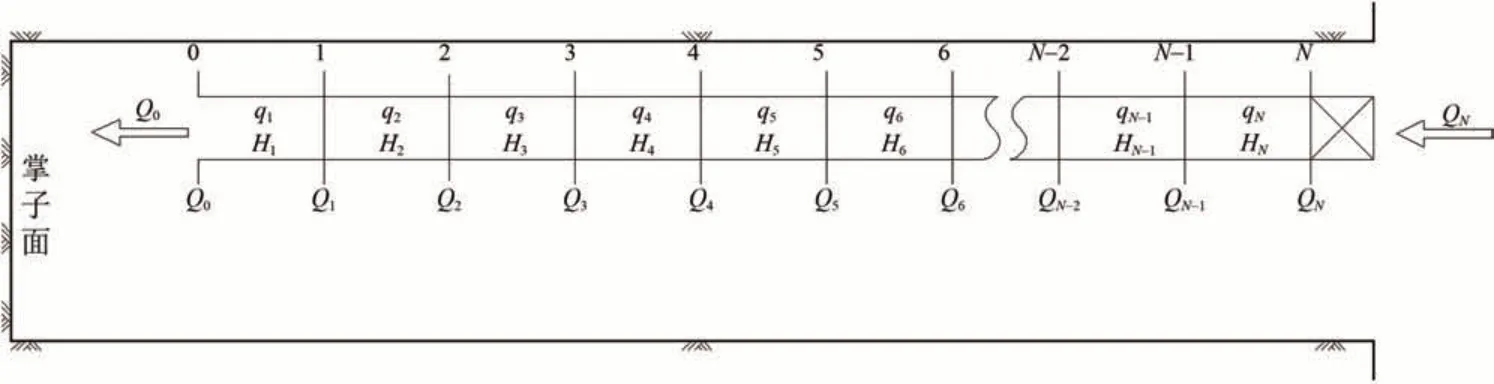
图4 分段迭代计算法示意图

根据达西阻力计算公式可得相邻段的风管静压迭代关系为

式中：r为管道沿程摩擦风阻，N· s2· m-3。

根据上节中的测试结果拟合式（4）推得单元段的风管漏风率为

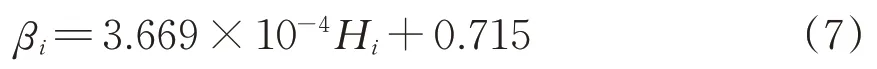
式中：βi为单元段的百米漏风率。

单元段的漏风量与其进口风量的关系为

由于空气密度近似不变，根据质量守恒可以推出相邻段的风管风量递推关系为

根据式（8）和式（9）可推出单元段的漏风量与其出口风量的关系为

管道沿程摩擦风阻r为

式中：λ为达西系数，取0.012～0.015；d为风管直径，m；l为单元段长度，取100 m；ξ为局部阻力系数；ρ为空气密度，m3·kg-1；A为风管横截面积，m2。

联立式（6）—式（10），不断迭代计算，可以依次求出每段漏风量qi，求和可得总漏风量Q为

整段风管的总漏风率M为

由总漏风率得出整段风管的平均百米漏风率β100为

应注意的是，由于每段的漏风量qi都和该段的平均风压有关，而前面已经漏掉的风量又会反过来影响风压H，所以没有办法导出1 个总和的计算式，只能不断迭代，最后求和。在实际应用时，可编程求解。

2.2 计算方法对比

以海拔高度1 000 m，工作面需风量25 m³·s-1，风管直径1.8 m 的隧道施工为例，采用分段迭代计算法和整段取平均静压计算法（简称直接计算法）的总漏风率计算结果对比如图5所示。

图5 总漏风率计算结果对比

由图5 可知：在通风距离较短时，采用分段计算法和直接计算法所得的总漏风率差异性较小，但是随着通风距离的增长，采用传统计算方法所得的总漏风率的差值逐渐增大；当通风距离达5 000 m时，两者的差距可达到16%，这是由于随着通风距离的增长，相比对一整段进行直接计算，分段迭代计算法的精度优势逐渐体现了出来。

3 漏风相关参数的影响性

由漏风率计算式可知，风管漏风率与通风距离、风管直径、海拔高度相关。采用基于分段迭代计算法的计算理论，并运用控制变量的计算方法，分析相关参数对风管漏风的影响程度。其中海拔0 m 时的掌子面需风量取25 m3· s-1。

3.1 通风距离

控制风管直径为2 m，海拔高度为1 000 m 不变，通风距离分别取500，1 000，1 500，2 000，2 500，3 000，3 500，4 000，4 500 及5 000 m 时，总漏风率和平均百米漏风率计算结果见表4。

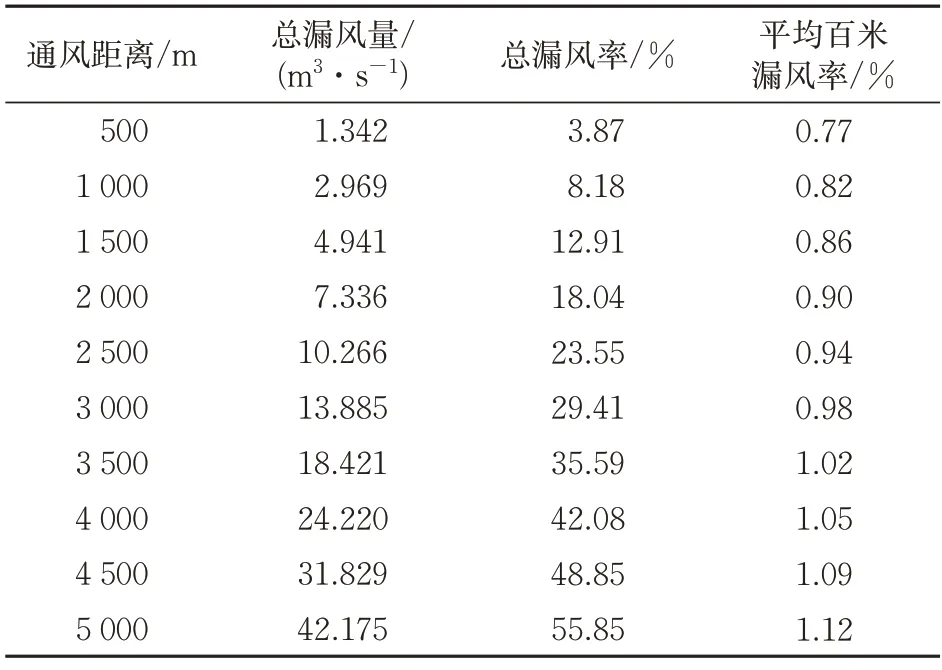
表4 典型工况下不同通风距离的漏风率解析解

由表4可知：随着通风距离增长，平均百米漏风率不断增大，通风距离从500 m 增长到2 500 m 后，平均百米漏风率增大22.1%；通风距离从500 m增长到5 000 m 后，平均百米漏风率增大45.4%；这是由于通风距离越长，风机所需提供的静压升高，而风管漏风率和静压成正相关。

为了减小整个通风段的静压等级，可尝试采用接力通风的方案。并且在长距离隧道中，采用接力通风能充分保证隧道施工通风的效果，提升隧道内施工工作环境，有效避免因灰尘、杂质等过多而影响工作人员的身体健康［14］。

接力通风是在隧道的中部设置增压风站，以达到串联增压的目的，从而继续向前送风。在进行总漏风率的解析计算时，假设在增压风站处风量不变（即风站处不产生额外漏风）。典型工况下不同通风距离风管分别采用单台独头压入式通风和串联接力通风的解析计算结果如图6所示。

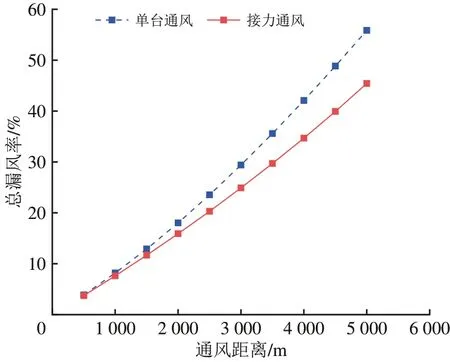
图6 2种通风方式下总漏风率对比

由图6 可知：随着通风距离的增长，采用接力通风的方式较单台通风方式的总漏风率减小幅度越来越大；通风距离为5 000 m 时，接力通风的方式比单台风机通风的方式总漏风率减小22.9%。当隧道通风距离较长时，为使工作面的新风量得以保证，可以采用2 台轴流风机接力通风的方式有效减小漏风率。

3.2 风管直径

控制海拔高度为1 000 m，通风距离为3 000 m不变，依然采用分段迭代计算法进行不同风管直径下的平均百米漏风率计算，风管直径分别取1.6，1.8，2.0，2.2及2.4 m时平均百米漏风率计算结果如图7所示。

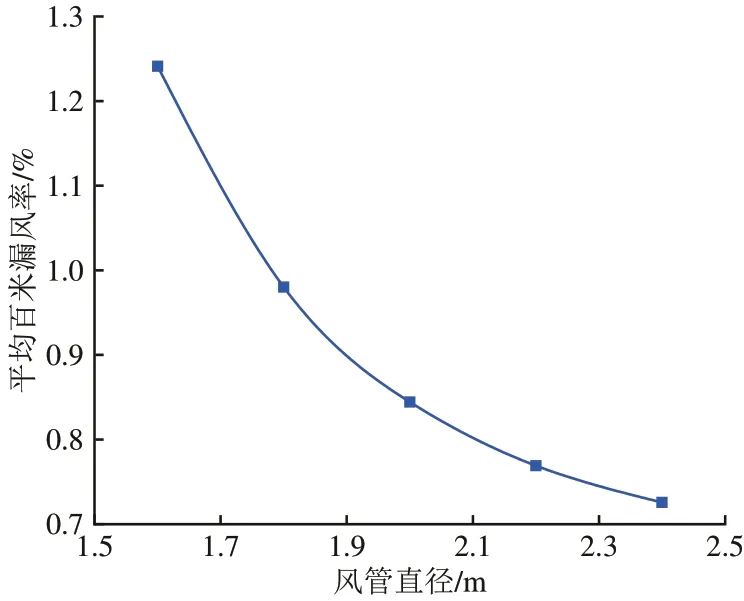
图7 不同风管直径下风管平均百米漏风率

由图7 可知：随着风管直径增大，漏风率显著减小；当风管直径从1.6 m增加到1.8 m时，平均百米漏风率减小了21.0%，从1.6 m增加到2.4 m时，平均百米漏风率减小了41.1%。

下面围绕分段迭代计算法中的数学原理对其进行结果分析。

根据独头压入式通风的工况类型，对摩擦风阻r的计算式即式（11）进行化简。风管横截面积A的计算式为

不考虑局部阻力系数ξ，空气密度ρ取1.11 m3·kg-1，管道达西系数λ取0.012，代入式（15），单元段通风距离为100 m 下的摩擦风阻r的计算式可化简为

分析式（16）可以发现，摩擦风阻r与直径的5 次方成反比，其函数曲线如图8 所示。由图8 可知：当风管直径不断增大时，管道的摩擦风阻减小的速率不断放缓；在风管直径小于2 m 时，增大风管直径对降低摩擦风阻具有显著效果。

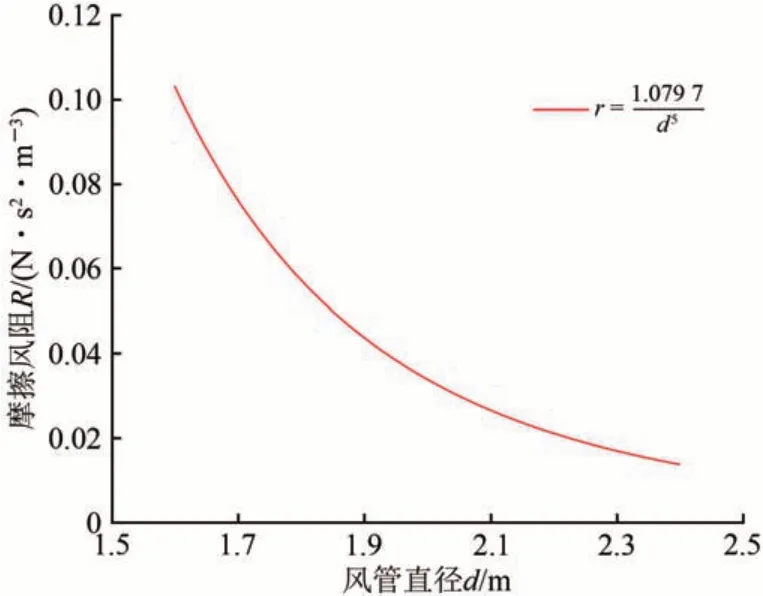
图8 摩擦风阻与风管直径的解析曲线

当摩擦风阻降低时，整个风管内所需提供的静压均减小。由于百米漏风率与静压成正相关，静压的降低将会使得每1 段的百米漏风率都减小，全段的平均百米漏风率也随之减小。

3.3 海拔高度

当海拔增高时，空气密度的降低会使得风管内的静压水平降低，不同海拔高度下的空气密度见表5。

表5 不同海拔高度下的空气密度

海拔增高后，由于气压降低使得炮烟体积膨胀，会导致掌子面需风量增加，进而又会使得风管所需的静压水平升高。按照目前最常用的稀释和排出内燃设备废气计算需风量的方式，需风量的修正系数可用CO海拔高度修正系数进行计算［15］，即

式中：fh为高海拔需风量修正系数；h为海拔高度，m；当h<400 m时，按fh=1.0计算。

以平原掌子面需风量为25 m³· s-1、风管直径为2 m、通风距离为3 000 m 的情况为例，综合考虑海拔高度对空气密度和需风量的影响后，求出不同通风距离下不同海拔高度的平均百米漏风率结果，如图9所示。

图9 不同海拔高度下风管平均百米漏风率的变化

由图9 可知：高海拔地区相对平原地区，需风量对应增加，在不改变风管直径的情况下，平均百米漏风率将增大。当通风距离为3 000 m，风管直径为2 m 时，海拔3 000 m 的高海拔地区相对于海拔500 m 的平原地区，需风量将增加至2.3 倍，平均百米漏风率将增大约1.7 倍。这是由于需风量的增长使得风机所需提供的静压升高，且需风量增长对静压的影响大于空气密度减小对静压的影响。

4 结论

（1）风管百米漏风率与管内静压成正相关，拟合得到了基于静压变化的百米漏风率计算式。

（2）隧道长距离风管压入式通风总漏风率的分段迭代计算法充分考虑了静压差和风量的沿程变化影响，在风管距离较长时，分段迭代计算法更为合理。

（3）随着通风距离增长，风机需提供的静压升高，平均百米漏风率也增大，采用2 台风机接力通风可有效降低风管的平均百米漏风率。

（4）随着风管直径增大，风管内的通风阻力减小，风机需要提供的静压降低，平均百米漏风率显著减小。因此，增大风管直径是改善风管漏风的有力措施。

（5）高海拔地区相对平原地区，需风量增加，在风管直径不变的情况下，平均百米漏风率也增大。