关注思维体验,发展关键能力
——以“与圆有关的概念”为例
江苏省无锡市华庄中学 刘振芹 周建平
纵观近几年的中考数学试题,不难发现题目均构思精巧且思维含量高,注重考查学生的关键能力和必备品格.因此,专题复习课的定位就要着力于学生思维的发展和关键能力的培养.那么,如何科学地选编复习题就显得尤为重要!笔者在2022年无锡市初中数学教研活动中执教了一节“与圆有关的概念”复习课,现就本节课如何以问题驱动指引学生的思维做回顾与思考,与同仁交流.
1 教学实例
1.1 问题情境,引发思考
引例若AB=5,BC=3,求AC.
生1:2.
师:你是怎么想的?
生1:点C在线段AB上,AC=2.
师:有没有不同想法的同学?
生2:8.
师:说说你的想法.
生2:点C在线段AB延长线上,AC=8.
学生的回答超出笔者的预设,根据回答,笔者启发学生再思考有没有其他情况.
图1
生3补充:△ABC是直角三角形且AB边为斜边时,AC=4.(笔者顺势请该生板演作图,如图1.)
追问:BC的位置确定吗?
笔者动手演示,学生意识到BC位置不确定.笔者继续引导:这样的点C有多少个?学生回答:无数个.这时强调AC并不是一个具体的取值,而是一个范围,最后引导学生给出点C的轨迹:以B为圆心,BC长为半径的圆(如图2).
设计意图:通过问题情境启发学生独立思考,在质疑情境中学生从特殊走向一般,再从一般走向特殊.既复习了圆的定义,又感受了运用确定性思维进行数学化思考的方法.这种创新概念复习的方式切实关注学生的思维体验,比直接让学生回忆概念,再用其解题的传统方式更能让学生达到对概念本质的理解.
1.2 问题拓展,搭建框架

图2
问题1 这张图(图2)清晰地呈现了点与圆的位置关系,有哪几种?如何判断点与圆的位置关系?
问题2 类比,直线与圆又有怎样的位置关系?
问题3 若在直径上取点D,大家能作出过D点的圆的最短弦吗?
学生通过板演作图和计算,感悟垂径定理的作用,如图3.
问题4 既然垂径定理涉及弧,那么弧的度数又与什么有关?
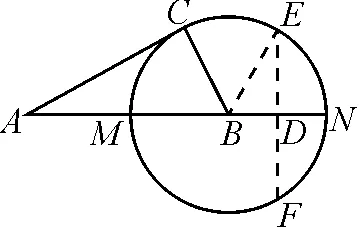
图3
问题5 当∠EBN=72°时,求∠EMN的度数.
学生通过计算回顾圆周角定理,如图4.
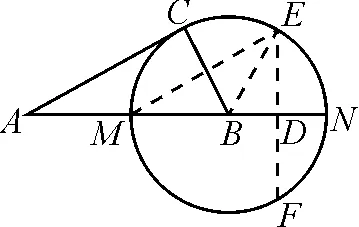
图4
最后,笔者引导学生回顾圆的中心对称性和旋转不变性,进而得到圆心角、弧、弦之间的关系.
设计意图:复习课是建构知识体系的过程,既要顾及基础知识,又要提高思维含量.因此,笔者通过设置有序的问题串,把“知识线索”转化为“问题线索”,引导学生在解决问题的过程中建构思维导图(如图5),进而从知识结构的视角实现思维的优化.
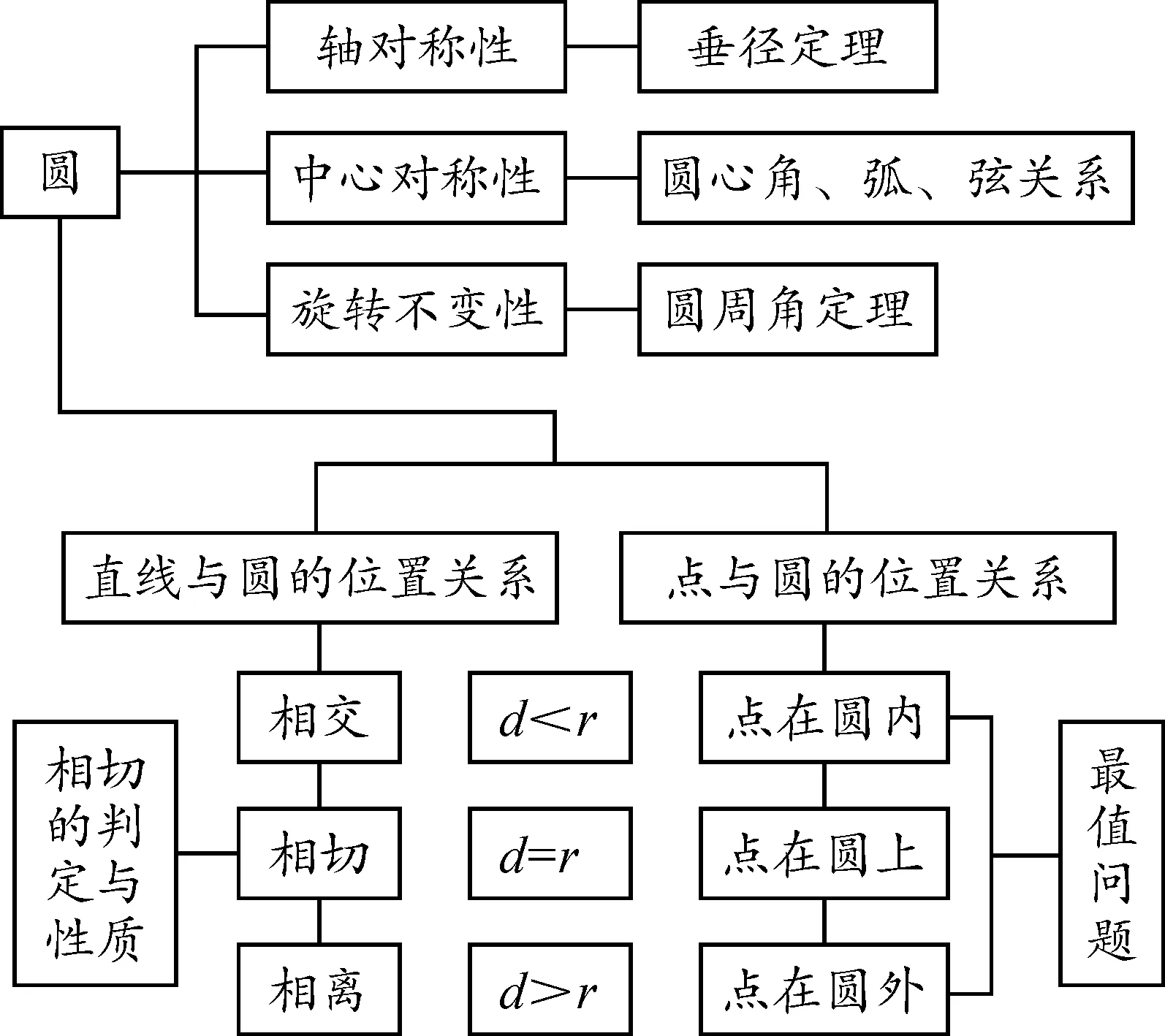
图5
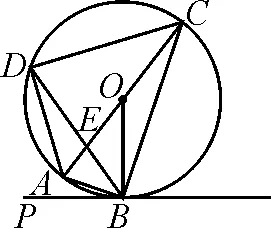
图6
体验中考(2021年无锡中考第25题)如图6,四边形ABCD内接于⊙O,AC是⊙O的直径,AC与BD交于点E,PB切⊙O于点B.
(1)求证:∠PBA=∠OBC;
(2)若∠PBA=20°,∠ACD=40°,求证:△OAB∽△CDE.
学生经过独立思考,给出证明思路.
生4:由AC是直径,得∠ABC=90°.由PB切⊙O于点B,得∠PBO=90°,故∠PBA=∠OBC.由∠PBA=20°,∠PBO=90°,得∠ABO=70°.又OA=OB,则∠AOB=40°,所以∠AOB=∠DCE.又∠DEC为△OBE外角,∠OBE=30°,得∠CED=70°,所以∠ABO=∠DEC,故△OAB∽△CDE.
师:有没有更简便的方法?
笔者适时总结,在解题方法多样化的基础上,引导学生关注方法的最优化,复习才能事半功倍.
设计意图:中考复习课的落脚点要回归到中考题,通过案例体验中考,让学生感受本节课复习的知识点是如何串联起来的,同时在书写的规范性以及方法的选择上引导学生.

图7
1.3 问题延伸,发展能力
1.3.1 一题多变,着力发散思维
例题如图7,在三角形ABC中,AB=AC,以AC为直径的⊙O交AB于点D,交BC于点E.
(1)求证:BE=CE;
(2)若BD=2,BE=3,求AC的长.
学生容易想到用三线合一证明BE=CE.求解AC的问题,学生给出了两种方法.

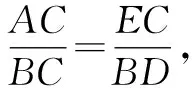

图8
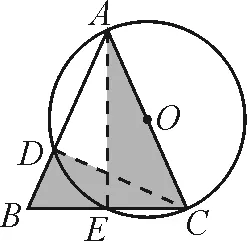
图9
笔者稍加点拨:你还能找出其他相似三角形来求AC吗?引导学生从相似角度,结合图形深入思考.
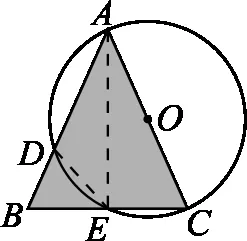
图10
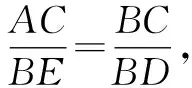
设计意图:本例题难度不大,通过勾股定理和相似两种思路思考问题,并挖掘相似的两种求解途径,让学生体验解题方法的多样性,在一题多解中有效培养学生的发散思维.
变式1如图11,在△ABC中,AB=AC,若点O在AC上向点C移动,以O为圆心,OC长为半径的圆交BC于E,ED⊥AB于D.求证:DE是⊙O的切线.
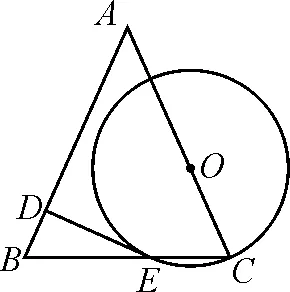
图11

图12
变式2如图12,在△ABC中,AB=AC=5,若点O在AC上向点C移动,以O为圆心,OC长为半径的圆与AB边相切,作ED⊥AB于D.若BD=1,求DE的长.
设计意图:变式1引起学生对直线与圆位置关系的关注,而变式2引导学生关注图形中相切的特殊位置关系,并为解决追问1和追问2作铺垫.这样一题多变的训练,不仅能加强知识的联系,还可培养学生的应变能力和发散思维能力,从而提升学生分析问题、探究问题和解决问题的能力.
1.3.2 多题一解,让发散走向集中
良好的思维品质除了要有发散性思维,集中思维也是不可或缺的一部分.集中思维以发散思维为基础,对学生思维能力的形成与发展具有重要作用.
接下来笔者在问题的本质上做延伸,促使探究更深一步,引领学生的思维更进一步.
学生对正弦条件有点无从下手,笔者适时引导.
师:正弦是什么图形里有的?
众生:直角三角形.
师:那么∠A所在的直角三角形有没有?
学生恍然大悟,意识到需要构造直角三角形,进而利用正弦定义建立方程求解.
教学中,笔者留给学生充分的时间进行观察和思考,直至学生认识到问题的本质.
追问2:若将变式2中的条件BD=1换成S△ABC=10,其余条件不变,求DE的长.
笔者在巡视中发现多数学生愁眉紧锁,说明他们不善于转化条件.于是启发学生思考:已知三角形的边长和面积,能确定什么?学生意识到面积条件可以转化为高,然后梳理出如下思路.
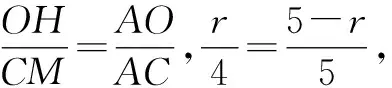
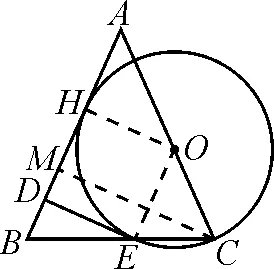
图13
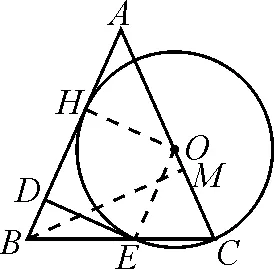
图14
师:若是作AC边上的高BM呢?
生7:△AHO∽△AMB,如图14.
总结:题目的背景没有变化,条件一直在变,但是面积条件本质上还是∠A的正弦值,所以我们在思考问题时要关注变中不变,即万变不离其宗的思考方法,这样才能得到从一题多解到多题一解的训练提升.
设计意图:追问1和追问2是对变式2条件的稍加改变,问题看似没有关联,但解决途径是一致的,目的是利用多题一解的训练,帮助学生感悟基本图形,感知问题的本质,提炼解题思想和方法,让思维从发散走向集中,提高综合应用的能力.
追问3:若将变式2中的条件BD=1换成BC=6,其余条件不变,求DE的长.
鼓励学生课后探索.
2 教学的进一步思考
2.1 思维诱发,需重视阅读理解能力
阅读能力是最基础、最关键的学习能力,而解决数学问题的关键就是要学会审题.审题并非将题目诵读一遍,而是在读题时抓住“题眼”,即试题的核心与重点,从而看透问题的本质.作为教师,应认识审题的重要性,舍得花时间精耕细作,让学生经历“怎么做—怎么来的—怎么想到的”思维提升过程,教给学生审题技巧,提高获取信息的能力,长此以往,学生的审题能力与解题能力将得以大幅度提升.
2.2 思维培育,要凸显独立思考能力
《义务教育数学课程标准(2022年版)》(以下简称新课标)明确指出,要使得人人都能获得良好的数学教育,不同的人在数学上得到不同的发展[1].不同的人在数学上得到不同的发展,主要表现在学生的思维力上.张楚廷教授指出:“教学,从根本上说,是思考着的教学引导着学生思考,又让思考着的学生促动教师思考.而在这一过程中,问题是最好的营养剂;在这一过程中,教师的思考和问题意识起着主导的作用.”[2]因此,在思维培育上,教师要多给学生一点思考的时间,多给学生一点表达的机会,让独立思考与自由表达自然形成思维能力.
2.3 思维优化,要突出语言表达能力
新课标明确提出,会用数学的语言表达现实世界.表达能力是学习能力的最高体现和综合反映.只有通过表达,知识才能被激活,才能真正被转化、升华为能力.学生用书面语言或口头语言从不同角度、不同侧面阐述看法或发表意见,这既是理解的重要标志,也是从理解到创新的关键一步.因此,教师要鼓励学生大胆地用自己的语言阐述自己的认识和想法,这样不仅能促进他们独立思考,同时也能活跃思维,在交流和互动中产生新颖的观点和思路,从而增强思维的灵活性和广阔性.

