高速铁路钢管混凝土尼尔森体系系杆拱纵向水平抗震能力评估

史航

（华设设计集团股份有限公司，南京 210000）

1 引言

随着我国交通强国战略的推进，我国高铁事业的发展日新月异，取得了举世瞩目的成就。钢管混凝土系杆拱具有承载力高、刚度大，对地质条件适用性好等优点，已广泛应用于50~160 m跨径的高铁桥梁。

目前，对于高铁桥梁抗震的研究主要集中于大跨度桥梁及高大桥墩的地震响应、抗震性能、减隔震分析等，较少见到高铁桥梁抗震能力评估研究，而当前结构抗震能力评估集中于房屋建筑领域。杨仕升[1]从结构强度与延性角度出发，研究了一种钢筋混凝土结构抗震能力评估方法；谢开仲[2-3]等以南宁永和大桥为背景，对钢管混凝土拱桥拱肋抗震能力以及整体破坏模式展开了研究；黄贤智[4]基于某主跨1 088 m公路钢箱梁斜拉桥，分析该桥各部分极限状态与延性能力，对其抗震能力进行评估；鲁冠亚[5]采用Opensees软件，基于增量动力分析，研究了高铁简支梁桥抗震性能指标；王学伟[6]在考虑梁轨相互作用以及地震动水压力对桥墩的作用基础上，对一座公铁两用跨海斜拉桥展开了研究，分析了其在强震作用下的各组成部分的破坏模式及易损性。

本文基于文献[1]所研究的抗震能力评估方法，针对某铁路桥梁进行部分调整，对该拱桥抗震能力进行评估，以期为类似桥梁设计提供参考。

2 结构概况

某铁路桥梁，梁部全长148 m，计算跨径144 m。梁部采用C55混凝土，梁端采用实心矩形截面，跨中采用单箱三室截面，吊点处设横梁。拱肋矢跨比为1∶5，矢高28.52 m，在横桥向内倾8°，拱肋面内方程为：Y=4×28.8（144X-X2）/1 442（以拱肋中心线与支座中心线交点为原点，即：x轴为顺桥向，距系梁顶面的距离为1.50 m；y轴为拱肋面内竖向）。拱肋横断面为高4.0 m的哑铃形，主管断面为φ1 300 mm×20 mm，腹板厚20 mm，管内灌注C55补偿收缩混凝土。拱肋间设1道一字撑（设于拱顶）和6道K撑。横撑断面为φ1 500 mm×24 mm，斜撑断面为φ900 mm×24 mm。拱肋及横撑均采用Q345qE钢材。吊杆采用127根φ7 mm低松弛镀锌平行钢丝（强度标准值为1 670 MPa），布置为尼尔森体系。全桥共设32对吊杆。结构总体布置如图1所示。

图1 桥梁总体布置图

3 有限元模型及地震动参数

3.1 有限元模型

有限元模型如图2所示。纵向系梁、主拱肋、拱肋横撑等采用空间梁单元；吊杆采用桁架单元。吊杆采用刚性连接与锚固处的主梁节点连接，不考虑下部结构对于梁部的影响。总计817个节点，764个单元。

图2 有限元模型

3.2 地震动参数

根据地质勘察报告，桥位处的场地特征周期为0.35 s，设防烈度为7度，其对应的多遇地震水平基本加速度为0.04g。

3.3 计算反应谱

本文所用反应谱是由GB 50111—2006《铁路工程抗震设计规范》设计反应谱调整而来。该设计反应谱仅适用于阻尼比为0.05的情况，钢管混凝土系杆拱拱桥分析时阻尼比采用0.03，参照GB 50909—2014《城市轨道交通结构抗震设计规范》中的相应公式对前述设计反应谱进行阻尼比调整。调整后的计算反应谱如图3所示。

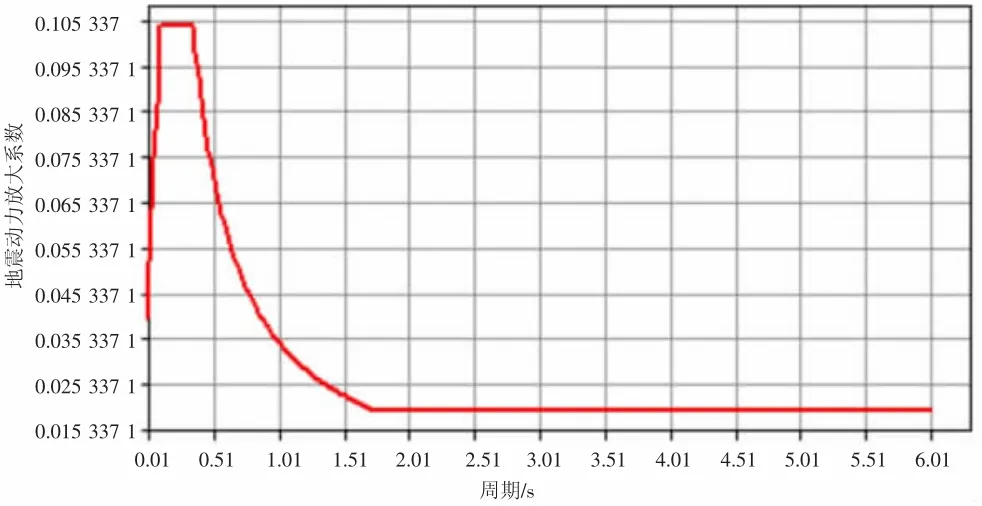
图3 调整后的计算反应谱

4 基本假定与理论

4.1 基本假定

假定当桥梁某部分或构件达到强度极限状态时，其任一结构单元的内力等于多遇地震作用下该单元内力的α倍加上恒载作用下该单元内力（α为部件屈服地震加速度系数）；假定对于桥梁各组成部分，其极限状态为强度破坏；假定对于各工况内力，其总体效应可以进行线性叠加。

4.2 基本思路

基于以上基本假定，以拱肋为例说明基本思路：主拱肋极限状态时内力为Fu，则Fu=F恒+αF多遇（F恒为恒载作用下结构内力；F多遇为多遇地震作用下结构内力；α为部件屈服地震加速度系数）。拱肋破坏为压弯破坏，则由组合模量法求得其P-M（轴力-弯矩）相关公式，将Fu=F恒+αF多遇代入相关公式中，反算出α，进而得到极限状态下水平地震加速度Ac′。基于结构弹塑性地震分析的等效线性法，引入塑性系数f估计延性对于耗散地震能量的贡献，Ac′f即为拱肋所能承受的最大水平地震加速度。

对桥梁各部件均进行以上分析过程，可得到各部件能承受的最大地震加速度Ai（i代表桥梁的第i个部件），Ai的最小值即为桥梁整体所能承受的最大地震加速度，可以以此来衡量桥梁的整体抗震能力。

4.3 桥梁各组成部分极限状态

拱肋破坏形态为压弯破坏。本文分析时以拱肋主钢管的强度达到极限作为主拱肋的破坏状态。拱肋主管的P-M相关公式采用组合模量法计算[7]，公式如下：

式中，N及M为拱肋主管所受轴力及弯矩；Nu及Mu为拱肋主管轴向极限承载力及弯矩；φ为稳定系数；η0为P-M曲线平衡点参数；a、b、c、d为拟合公式系数。各参数除N、M及φ外，计算取值详见文献[7]。

拱肋主管的稳定系数φ采用等效梁柱法计算，等效计算长度参照GB 50623—2013《钢管混凝土拱桥技术规范》取0.36倍拱轴线长度。

由于本文以拱肋主管的破坏来表征主拱肋破坏，计算分析时主拱肋所受内力应分配至各拱肋主管。分配各拱肋主管所承受内力时应考虑其承受的弯矩，以考虑偏心对于各主管承载能力的削弱。主管内力分配计算可参照GB 50923—2013《钢管混凝土拱桥技术规范》，公式如下：

式中，N1、N2及M1、M2分别为分配到两个拱肋主管上的轴力及弯矩；η1为单根拱肋主管和整个主拱肋弯曲刚度之比；h1为两拱肋主管在受弯截面内的中心距。

横撑为空心钢管，破坏形态为压弯破坏。本文计算时，不考虑横撑的局部屈曲。横撑破坏时，认为其全截面都达到极限应力，相应强度按GB 50017—2017《钢结构设计标准》计算。

吊杆主要承受拉力，其破坏形态为受拉破坏，其极限强度参照JT/T 775—2016《大跨度斜拉桥平行钢丝拉索》，取9 091 kN。

纵向系梁为预应力钢筋混凝土结构，正常状态下全截面受压，其破坏按照受弯破坏及截面消压双重控制，受弯破坏极限承载力按照TB 10092—2017《铁路桥涵混凝土结构设计规范》计算。

4.4 地震作用塑性系数f

基于结构弹塑性地震分析的等效线性化方法，延性系数为μ的结构或构件，可等效为一个完全弹性系统，该弹性系统的地震力为该结构实际所受地震力的1/f倍。则在考虑延性的情况下，该结构或构件所能承受的最大水平地震加速度即为Ac′f。

参照等效线性化的能量一定及位移一定原则，在反应谱能量一定区域内，取在位移一定区域内，取f=μ，其余数值通过线性插值确定。

本文所用反应谱中，取反应谱平台段为能量一定区域，大于5Tg（Tg为反应谱特征周期）段为位移一定区域。文献[1]中计算f时采用结构基频，考虑到动力分析显示，本桥首个纵向平动为主的振型为第十阶，本文f采用前十阶振型对于振型参与系数的加权平均。

为确保结构安全性，不宜直接采用延性系数μ计算地震作用塑性系数f，而引入安全系数控制结构所能利用的延性。对于场地卓越周期较大者，该安全系数可取1/2，其余场地可取2/3，本文取1/2。

4.5 各组成部分延性系数计算

主拱肋延性系数μ取拱肋主管强度控制截面的曲率延性系数，即控制截面的截面极限曲率与屈服曲率之比。本文计算时，采用文献[7]中的圆钢管混凝土M-φ（弯矩-曲率）滞回模型拟合公式计算。

横撑与吊杆延性系数μ，取材料的强度极限应变与弹性极限应变之比值。本文计算时，横撑强度极限应变取0.01，吊杆强度极限应变取0.035，横撑与吊杆极限弹性应变取值参照相关规范。

系梁延性系数计算时，将系梁视为恒载下的压弯构件，采用GB 50010—2010《混凝土结构设计规范》（2015年版）本构模型，预应力钢筋按弹模比换算为普通钢筋。

5 计算结果

计算结果详见表1、表2。

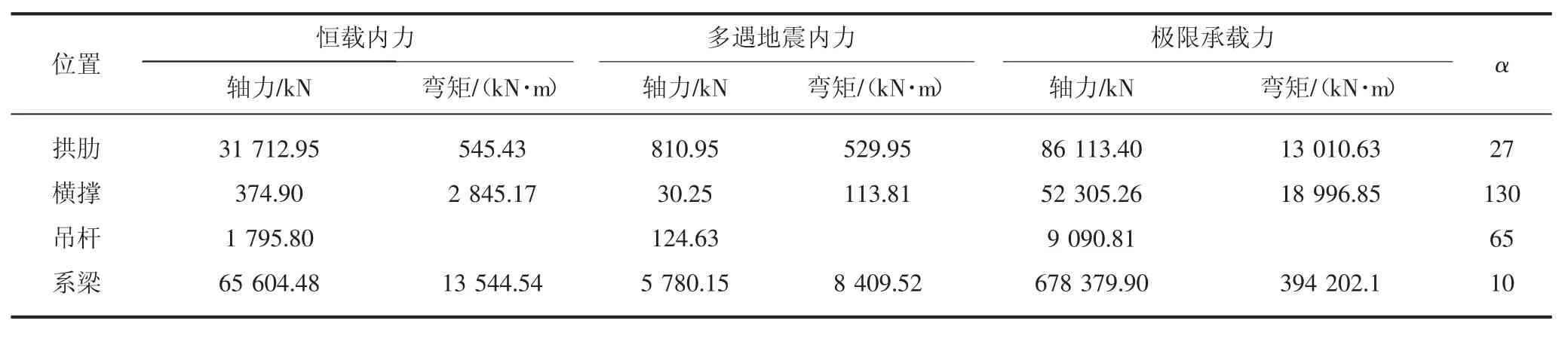
表1 各部件内力结果（最不利位置）

表2 各部件所承受最大水平地震加速度（最不利位置）

结果表明：尼尔森系杆拱具有良好的抗震能力，纵向水平地震作用并不控制梁部设计；系梁消压是本桥纵向地震作用下控制破坏模式；拱脚作为联系拱肋与系梁的关键部分，其安全性是系杆拱设计成败的关键之一。

6 结语

分析表明，本文所采用的方法能较为有效地对高铁钢管混凝土系杆拱的抗震能力进行初步评估，可较为简便地确定桥梁结构所能承受的最大地震地面加速度与可能的抗震薄弱环节，为进一步的详细分析奠定了基础。但由于本文方法采用了一定的简化假定，后续分析中应结合增量时程分析等方法才能精确的判定桥梁结构的抗震能力。

希望本文能给相关设计人员一些启发和思考，并为类似工程提供参考借鉴。