复杂空间结构屋顶径向主梁的吊装技术研究

邢耀安

（中铁21局集团有限公司第二工程公司,甘肃 兰州 730000）

0 引言

吊装技术作为建筑工程最为广泛高效的竖向运输方式，不论是高层建筑还是大跨建筑结构施工都有着广泛的应用，但也存在着一定的局限性，如施工难度大、难以保证施工质量、容易发生安全事故等问题。在这样的背景下，通过理论分析、结合计算机辅助计算，使得吊装技术得以发展、应用于施工困难和重大的工程中。

为研究复杂空间结构屋顶径向主梁的最佳吊装方法，学者们对其进行了大量的试验研究，结合工程实例，对钢结构吊装技术做了较为详尽的阐述。范基等[1]研究了1 800 t钢闸室整体吊装过程中液压千斤顶同步提升技术。杜民和杨堃[2]研究了吊装过程中的吊点数量、吊点位置及网架提升速度的同步性，对吊点数量与位置进行了优化。陈国栋等[3]利用数值分析软件对吊装的全过程进行了动态的数值仿真模拟，深入分析了吊装施工和不同的支撑拆卸过程的结构受力情况。张冰[4]结合最小应变能原理和一种目标函数满意度的方法实现了大跨度空间结构吊装施工的吊点优化布置。罗尧治和董石麟[5]在MSTCAD的软件平台上新开发了吊装施工模块。高树栋等[6]主要研究了桁架柱单机吊装技术、双机抬吊技术、主桁架3机吊装等施工技术，最后总结了一整套主体结构吊装的安装措施。刘学武等[7-8]提出一种可应用于吊装平衡系统的简化椭圆计算方法和优化迭代算法，使得各吊索截面内力相等。熊学炜[9]在多体动力学理论的基础之上，提出了适用于数值仿真模拟的大型钢结构施工过程的方法策略和实施步骤。陈博文[10]利用MATLAB改进了进化规划算法，通过后台调用计算结构的应变能，来寻求最优吊点布局方案。左川等[11]研究了钢结构桁架分段位置、临时支撑架布置及钢结构桁架分段吊装施工工艺及方法。曹世伟等[12]详细介绍了桅杆吊装技术的优点、施工方法及经济效益。刘松[13]主要研究了建模技术与仿真系统的构建技术，通过在实际工程中搭建了钢结构虚拟施工平台的系统框架，实现了其吊装施工过程的模拟。李伟男[14]通过对施工方案的比对和吊装过程的模拟验算，得出不同吊装方法的各自优缺点和适用范围。彭仪普和朱铎义[15]通过对大跨度超重悬挑钢结构分段吊装法和整体吊装法的吊装效果进行分析，研究结构的根部和支撑杆受力情况。张辉[16]采用滑移法施工，克服了大型施工机械无法一次就位的问题，提高了施工效率。张盛华[17]通过理论分析和数值模拟，对两种不同的布点方式进行了研究，为钢梁的吊点选择提供了理论支撑。潘剑峰等[18]在深基坑+大型钢结构的施工中，利用大型汽车吊在狭小的深基坑施工场地内开展有序的安装施工并进行研究。吕永涛[19]通过理论分析得出了网架结构不同的吊点位置对网架结构整体的影响，给出了最佳吊点位置的判别方法。吴亚芳[20]通过精准控制施工过程中各道工序，顺利完成了空间曲线造型钢结构吊装。

由此可知，对于研究钢结构吊装施工技术和施工方法较为丰富，但都仅限于结合具体工程实例所得出的研究成果，难免有其天然的局限性。因此，通过具体工程，针对工程中特种形状钢构件的吊装定位并辅以有限元数值方法，给出了最不利吊装构件的合理吊装方法。

1 工程概况

天水市麦积山景区游客服务中心总建筑面积为1.6万m2，为空间环形钢架体系，工程钢结构用钢量8 600 t，直径跨度147 m，屋顶结构最高点标高为23.3 m，平均高度17.4 m，钢柱柱脚插入下部混凝土至基础顶，整体钢结构包括内圈环柱体系、外圈环柱体系，如图1所示。屋顶径向主梁最大跨度42 m，单根梁重达19 t，且全部为现场吊装，工程结构体系复杂，施工精度高、难度大。

2 屋顶径向主梁吊装技术研究

2.1 吊点位置的计算

主梁一般均为等截面构件，假设其质量均匀分布，基于此，对等截面构架的理论吊点位置进行计算。

（1）单点起吊

单点起吊一般应用于等截面柱，柱子的一端点与地面接触，在柱身设置一吊点，对应计算模型可简化为一端悬臂的简支梁，如图2所示。

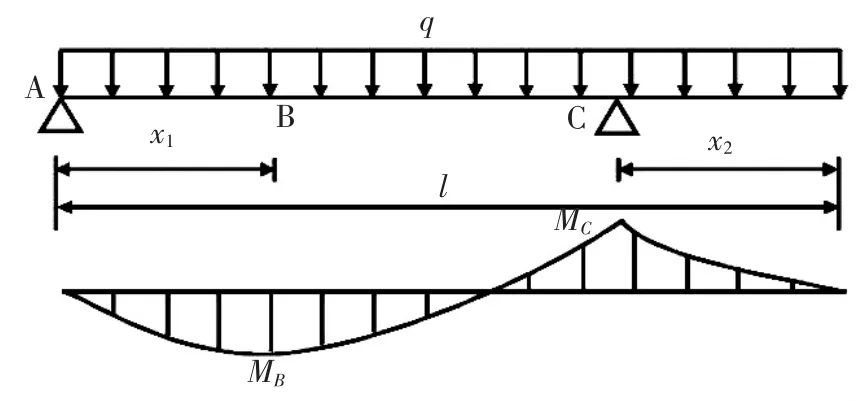
图2 单点起吊简图

构件自身承重为均布荷载，对于最佳吊点的选取，仅需取梁轴线内正负弯矩绝对值相等，即MB=MC，且弯矩达到最小值。

图2中，假设B点为最大正弯矩处，依据静力平衡和B点剪力为零，计算得到：

由MB=MC，可得：

求解式（2）得到：

得到单点起吊的吊点位于构件一端的0.293 l处。

（2）双点起吊

双点起吊对于吊点的位置确定也是以构件正负弯矩绝对值最小为准则，此时的吊绳一般位于构件中心点的两侧，且对称。计算时简化为两端悬臂的简支梁，如图3所示，此时只要确保MA=MB=MC，即可得到最佳吊点位。

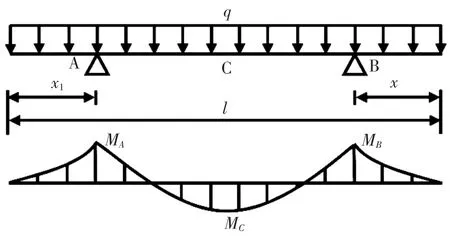
图3 双点起吊简图

从图中可以看出，C点为最大正弯矩所在处，且x1=x2，根据静力平衡可得A和B点的反力FA和FB，即可得到吊点处的2个弯矩MA和MB：

又有弯矩MC为：

将式（3）、式（4）代入到MA=MB=MC中，可得：

得到双点吊装的吊点理论位置处于距梁端点0.207 l处。

（3）三点起吊

三点起吊一般适用于长度较大且截面较小的构件。对于等截面细长构件的三点吊装技术，首先选取构件中心处为一吊点，其余两吊点选取在杆件中心的两侧，三点起吊的计算简图如图4所示。

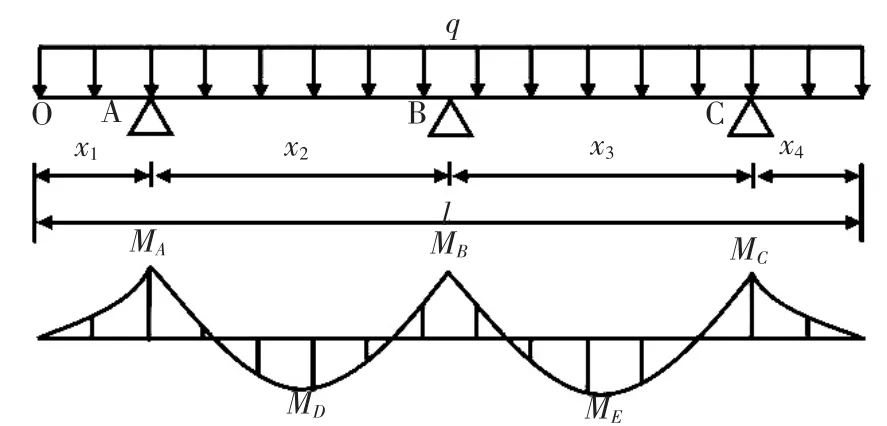
图4 三点起吊简图

图4中3个吊点处的弯矩MA、MB和MC分别为：

式中：FA为A点的支座反力。弯矩MD和ME分别为：

式中：FB为B点的支座反力，xAB、xBC分别为AB跨与BC跨内剪力为零的位置至端点O的距离。当对构件进行三点吊装时，根据式（6）-式（10）进行组合计算，得到当MA=MD=ME=MC时，结构的弯矩极值最小，得到最佳吊点位置为：

且吊点的反力、约束位置均是对称分布的。

（4）四点起吊

针对于等截面超长构件四点吊装技术的研究，一般选取的4个吊点位于构件中心两侧，如图5所示为四点吊装技术的理论位置和计算简图。

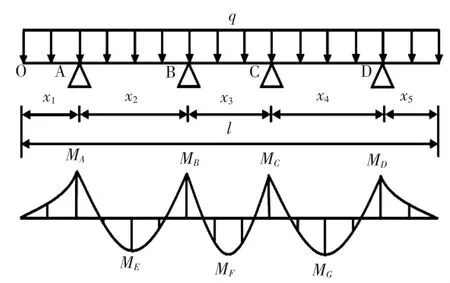
图5 四点起吊简图

图5中，4个吊点处的弯矩MA、MB、MC和MD分别为：

式中：FA和FD分别为A点和D点的支座反力。弯矩ME、MF和MG分别为：

式中：xAB、xBC和xCD为AB、BC和CD跨内剪力为零位置处至端点O的距离。当对构件进行四点吊装时，根据式（11）-式（17），同时结合静力学平衡进行组合计算，得到当MA=ME=MB=MC=MG=MD时，结构的弯矩极值最小，求解得到：

此时，吊点的反力、约束位置均是对称的。

2.2 屋顶径向主梁的力学性能分析

最不利的单根屋顶径向主梁安装标高为16.452～19.683 m，长度为34.3 m。由于该构件的长度大，基于现场真实情况，拟采用三点吊装和四点吊装，钢梁截面为H型钢，Q345B钢材，弹性模量为2.06×105MPa，泊松比为0.3，密度为7 850 kg/m3，截面尺寸为900 mm×400 mm×20 mm×25 mm，长度取35 m。吊装过程使用ANSYS有限元软件进行仿真模拟，杆件使用beam189梁单元。

（1）挠度

2种吊装方法下最不利屋顶径向主梁匀速上吊过程中的横向变形如图6所示。

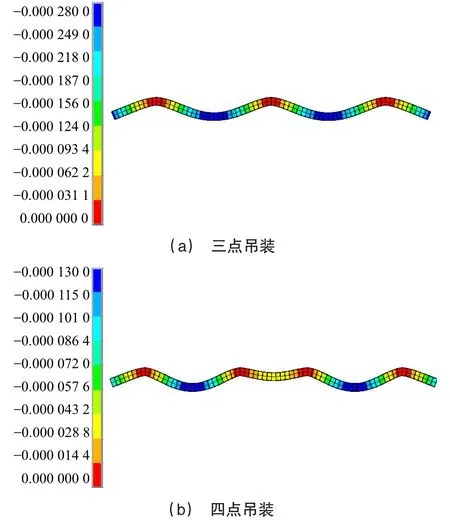
图6 钢梁吊装挠度图

由图可知，三点吊装下，单根最不利屋顶径向主梁的挠度为0.280 mm；四点吊装下，单根最不利屋顶径向主梁的挠度为0.130 mm。两种方法下，变形都很小，均小于l/400=87.5 mm，满足《钢结构设计标准》（GB50017—2017）[21]的要求。

（2）应力

2种吊装方法下最不利屋顶径向主梁匀速上吊过程中的应力如图7所示。

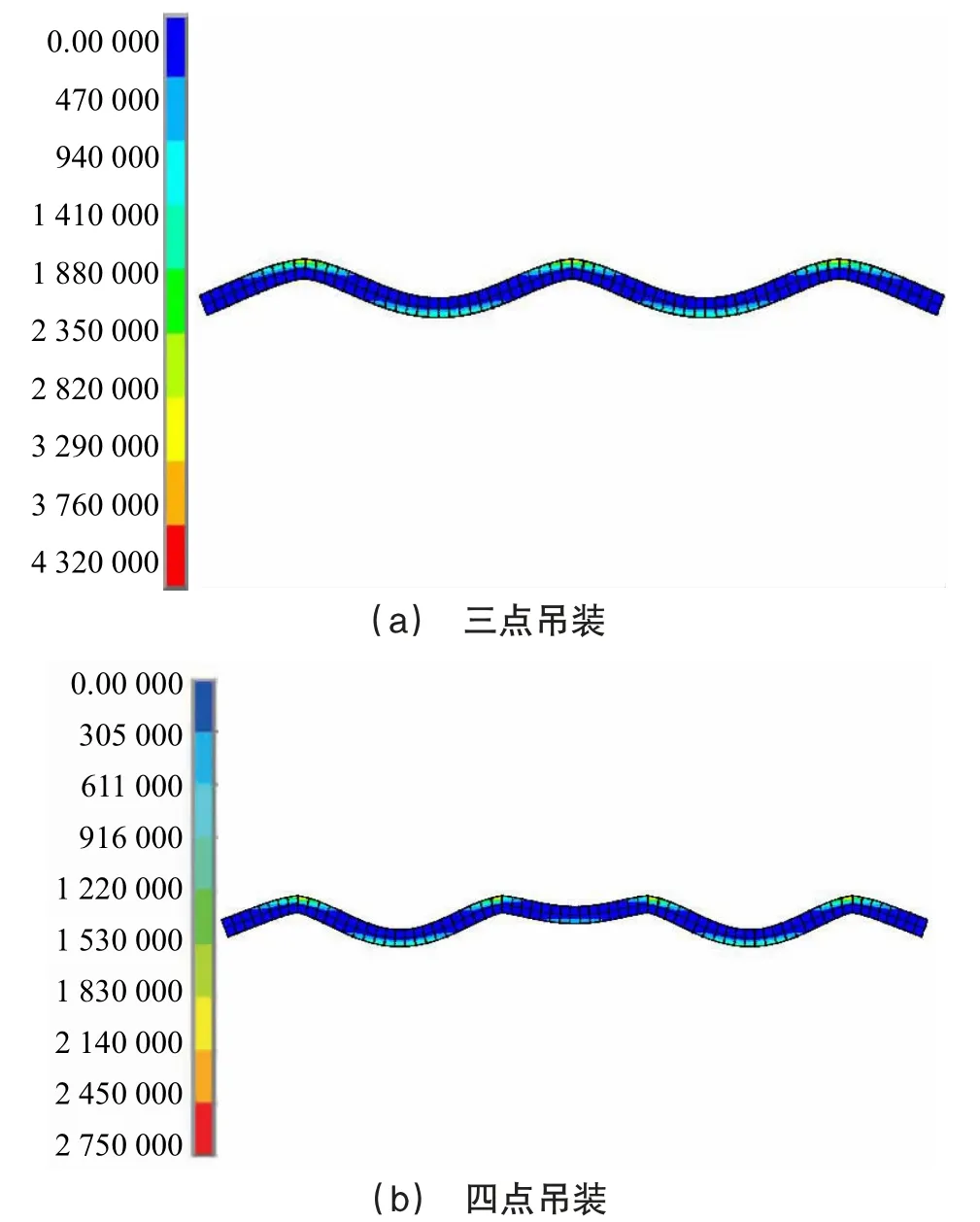
图7 钢梁吊装应力图

由图可知，三点吊装下，单根最不利屋顶径向主梁的最大应力为4.23 MPa，位于钢梁上翼缘吊点处；四点吊装下，单根最不利屋顶径向主梁的最大应力为2.75 MPa，位于钢梁上翼缘吊点处。

3 结论

（1）等截面构件单点吊装的最佳理论吊点在主梁端的0.293 l处；双点吊装的最佳理论吊点位置在距离主梁两端的0.207 l处；三点吊装的理论位置在主梁的跨中位置和距离两端的0.138 l处；四点吊装的最佳理论位置在距离主梁两端的0.104 l、0.396 l处。

（2）利用有限元软件对单根最不利屋顶径向主梁在三点吊装和四点吊装进行数值计算，研究得到在两种吊装方法下屋顶径向主梁的横向挠度均满足规范要求。

（3）根据数值结果得到主梁的吊点处均会产生应力集中现象，但四点吊装下主梁的力学性能优于三点吊装方法，为类似工程提供了一定的技术指导。