基于多因素模型和多尺度遗传算法的复杂曲面喷涂轨迹综合优化
朱永国 ,王 鑫,刘林辉,卓 鑫,胡慧顺
(1.南昌航空大学 航空制造工程学院,江西 南昌 330063;2.江西江铃集团车桥齿轮有限责任公司,江西 南昌 330000)
0 引言
喷涂机器人作为面向喷涂作业的工业机器人,被广泛应用于飞机表面喷涂[1]。飞机表面为复杂曲面,传统示教编程已无法满足其高效率、高精度喷涂的要求[2]。针对复杂曲面喷涂轨迹优化难题,国内外研究人员进行了相应的研究。涂层厚度分布模型是复杂曲面喷涂轨迹优化的基础。王国磊等[3-4]在分析航空产品喷涂工艺的基础上,建立了面向机器人喷涂的多变量涂层厚度分布泛化模型。ZHOU等[5]考虑到复杂曲面的涂层均匀性难以保证,提出利用倾角喷涂的机器人轨迹优化方法。曾勇等[6]和刘亚举等[7]针对复杂曲面圆弧犄角区域涂料浪费严重,涂层厚度分布不均的问题,提出高斯和倾角的新型喷枪模型。基于涂层厚度分布模型,CHEN等[8-9]分别采用矩形模型和指数均值贝塞尔法设计复杂曲面的机器人的喷涂轨迹。张鹏等[10]针对不同类型曲面轨迹连接问题,建立了直纹曲面喷枪模型,以提高曲面连接处的涂层厚度均匀性。GUAN等[11]基于不同的法向量夹角,对直线、凸弧和凹弧组合的相邻面片连接处的过渡段进行优化,提高了曲面过渡喷枪参数选择的灵活性。SETHURAMALINGAM等[12]结合模糊专家系统与田口分析,建立了基于真值模糊逻辑的表面粗糙度评价模型。马淑梅等[13-14]针对复杂曲面,拟合了复杂表面各点的涂层厚度数据,建立了涂层厚度生长模型。
以上机器人喷涂轨迹研究,通过建立涂层厚度分布模型,并以涂层厚度均匀性为目标优化了喷涂工艺参数,但喷涂轨迹本身的量化评价指标仅为轨迹长度、轨迹转角等。当喷涂对象为飞机产品复杂曲面时,喷涂轨迹复杂,量化评价指标亟待完善。为此,针对复杂曲面喷涂轨迹的量化评价指标不够完善,本文提出基于多因素模型和多尺度遗传算法的复杂曲面喷涂轨迹综合优化方法,以满足飞机等航空航天产品复杂曲面喷涂需求。
1 机器人喷涂轨迹多因素模型构建
喷涂轨迹影响因素主要有:①机器人的喷涂稳定性,机器人的喷涂稳定性影响其控制难度,稳定性不足导致复杂曲面的涂层厚度均匀性下降;②喷涂效率,机器人的喷涂效率影响生产节拍;③喷涂轨迹干涉,喷涂轨迹干涉直接影响曲面涂层均匀性。为此,构建机器人喷涂轨迹多因素模型,该模型包含喷涂稳定性模型、喷涂效率模型和喷涂轨迹干涉模型。
1.1 喷涂稳定性模型构建
如图1所示,Qi表示喷涂轨迹点,n表示轨迹点数量,θi表示向量Qi-1Qi与QiQi+1的夹角:
i=0,1,2,…,n。
(1)

式中:θi<θmax(θmax为转角阈值),喷枪经过此处的喷涂稳定性所受影响较小;θi>θmax,喷涂稳定性较差。
(1)转折点总数
当θi>θmax时,记该点为转折点,
(2)
式中:Qi-tra表示喷涂轨迹第i点是否存在转折,Ni-tra表示喷涂轨迹的转折点总数。Ni-tra越小,喷涂轨迹转折点越少,机器人喷涂稳定性越好。
(2)平均轨迹转折度
为量化表征每段轨迹的弯曲程度,定义平均轨迹转折度
(3)
式中:n1表示喷涂轨迹段数;Nb-tra表示第b段喷涂轨迹的转折度。
(4)
式中:θa-tra表示第b段轨迹上第a个轨迹点的转折度,n2表示第b段轨迹的轨迹点数。Nave越大,轨迹点之间的转角就越小。
综合式(2)和式(3),并对二者标准化,定义喷涂稳定性量化指标
(5)
式中:wNi、wNa表示转折点总数和平均转折度权重。fsta越小,机器人的喷涂稳定性越好。
1.2 喷涂效率模型构建
(1)轨迹总长
喷涂轨迹的总长越小,机器人的喷涂效率越高。采用空间网格计算轨迹点的距离,构建轨迹点距离矩阵Tlen:
Q0…Qj…Qn
(6)
式中l(i,j)表示第i点和第j点的距离。
利用式(6),定义喷涂轨迹总长Lsum为:
(7)
式中lb表示第b段轨迹的长度。Lsum越小,喷涂轨迹越短,机器人的喷涂效率越高。
(2)轨迹中位数长度
不同区域的喷涂轨迹段,通常采用不同的喷枪移速和流量来保证曲面喷涂质量。二者频繁变化,导致机器人整体喷涂效率下降。因此,应增大各段轨迹的长度,以减少喷枪移速和流量的变化次数,从而提升机器人的喷涂效率。中位数不受轨迹段长度最大、最小值的影响,可用于描述轨迹段长度的集中趋势。为此,引入中位数,对轨迹段长度进行排序,定义喷涂轨迹段的中位数长度Lmid为:
(8)
式中rem(n1,2)表示n1对2取余。Lmid越大,机器人喷枪移速和流量变化次数少,喷涂效率越高。
综合式(7)和式(8),并对二者进行标准化,定义喷涂效率综合评价指标feff为:
(9)
式中:wLs、wLm分别表示喷涂轨迹总长和中位数长度的权重。feff越小,机器人的喷涂效率越高。
1.3 喷涂轨迹干涉模型构建
如图2所示为复杂曲面的3种喷涂轨迹干涉类型。
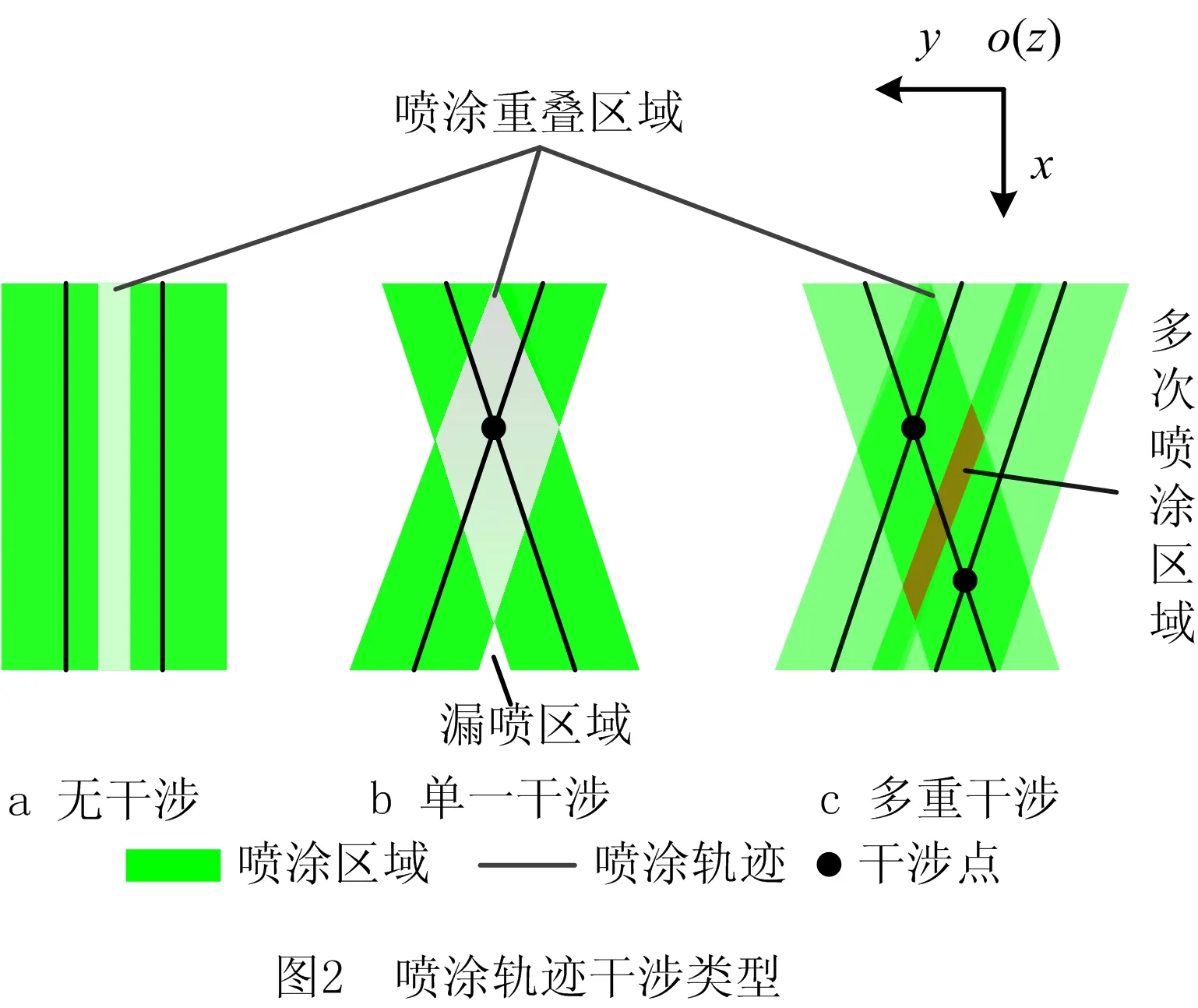
为量化表示喷涂轨迹段之间的干涉程度,构建喷涂轨迹干涉矩阵Tint:
p0…pc…pn1
(10)
式中p={p0,p1,p2,…,pb,…,pn1}表示喷涂轨迹段。
定义p(b,c)表示轨迹段pb与pc的干涉情况,
(11)
利用干涉矩阵Tint和p(b,c),定义某一段喷涂轨迹的干涉度:
(12)
式中Nb表示第b段轨迹的干涉度。
(1)中位数干涉度
对干涉度大小进行排序,定义中位数干涉度Nmid:
(13)
式中Nmid越大,轨迹干涉越严重,复杂曲面涂层均匀性越差。
(2)总干涉度
定义喷涂轨迹总干涉度Nsum:
(14)
式中Nsum越大,轨迹干涉越严重。
综合式(13)和式(14),并对二者标准化,定义机器人喷涂轨迹量化指标fint:
fint=wNmNmid+wNsNsum。
(15)
式中:wNm、wNs分别表示中位数干涉度和喷涂轨迹总干涉度的权重。fint越大,喷涂轨迹之间的干涉越严重,复杂曲面喷涂质量难以保障。
综合式(5)、式(9)和式(15),构建机器人喷涂轨迹多因素模型:
(16)
式中Ffea表示喷涂轨迹的综合评价指标。Ffea越大,喷涂轨迹使机器人具有较高的喷涂稳定性、喷涂效率及较低的干涉程度,以满足复杂曲面喷涂质量需求。
2 多因素模型因素权重确定
喷涂轨迹多因素模型中,不同因素对喷涂轨迹的影响力不同,须针对不同因素分配不同的权重,以合理设计适应度函数。喷涂轨迹评价因素的权重分配为复杂、模糊决策问题,且决策因素之间具有相对独立性,采用传统权重分配方法准确性较低。层次分析法(Analytic Hierarchy Process, AHP)结合定性、定量分析,可解决复杂、模糊问题的决策分析。针对决策因素轨迹转折点、轨迹长度、干涉度,构造层次判断矩阵Thie:
(17)
式中E11~E33表示决策因素的标度。对层次判断矩阵进行一致性检验:
(18)
式中:CR表示一致性比率,λmax表示最大特征值,nE表示决策因素总数,RI表示随机一致性指标。根据式(18)中λmax的特征向量ξ,确定决策因素权重,从而确定适应度函数:
(19)
式中:ωg表示第g个决策因素的权重,ξg表示特征向量。
3 基于多尺度遗传算法的喷涂轨迹综合优化
3.1 遗传算法多策略优化
求解机器人喷涂轨迹多因素模型的核心在于求解轨迹点的最优序列,是离散型组合优化问题。组合优化搜索空间较大,难以采用数值法直接求解。遗传算法(Genetic Algorithm, GA)在解决此类问题时,具有较好的优化速度和优化效果。但是,经典遗传算法的种群进化过程无梯度信息,仅通过个体之间的选择、交叉、变异来诱导种群进化,易出现早熟及搜索精度不高的现象。针对遗传算法存在的不足,提出多尺度遗传算法(Multi-scale Genetic Algorithm, MsGA):①采用多尺度进化策略,在不增加算法时间复杂度的前提下,对种群个体多尺度聚类,使不同尺度的个体互相竞争和配合,在可行域中并行搜索;②采用动态进化策略,使种群个体在不同进化阶段拥有不同的交叉、变异概率,进行分散式搜索。
3.1.1 种群多尺度进化

Nnum=⌈Nmax/Nmul⌉。
(20)
式中⌈⌉表示向上取整。
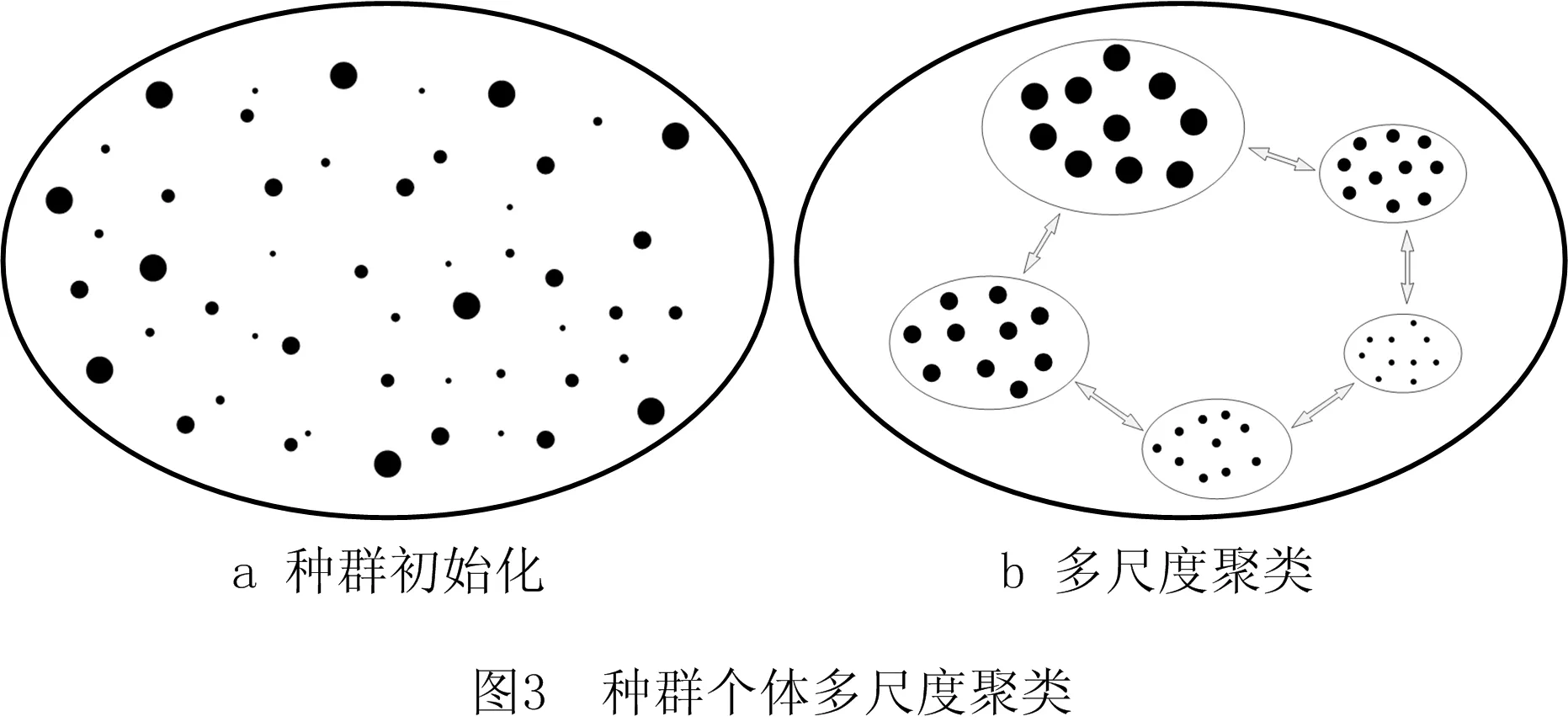
不同子群个体的适应度函数值不同,促使子群多尺度进化。同时,若多次迭代后,子群的适应度函数最大值无变化,则共享种群最优个体,以维持种群的多样性,使子群在互相竞争配合中实现并行搜索。
3.1.2 进化概率动态调整
进化概率过小,算法搜索效率较低且容易过早收敛;进化概率过大,算法转变为随机搜索状态,收敛性较差。为保证算法的收敛速度及收敛精度,结合个体的适应度函数值和迭代次数,定义种群进化概率:
(21)
(22)

综上所述,采用多尺度、动态进化策略改进经典遗传算法,使各子群多尺度动态遗传,从而推动种群个体在互相竞争和配合中不断进化,逐步达到最优解。
3.2 机器人喷涂轨迹综合优化
如图4所示,利用多尺度遗传算法,完成机器人喷涂轨迹综合优化。

步骤1初始化。设置种群规模Nmax,最大迭代次数K,子群个数Nmul,进化概率最值Pcro-max、Pcro-min、Pvar-max、Pvar-min,进化尺度因子μcro、μvar,随机初始化种群个体,即喷涂轨迹点序列,记种群进化代数k=0。

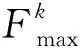
步骤4交叉变异结束判断。若Nchi=Nmul,所有个体均完成交叉变异,转步骤5;否则,转步骤3。
步骤5最优个体共享。若多次进化后,子群个体的适应度函数最大值无变化,共享种群最优个体。
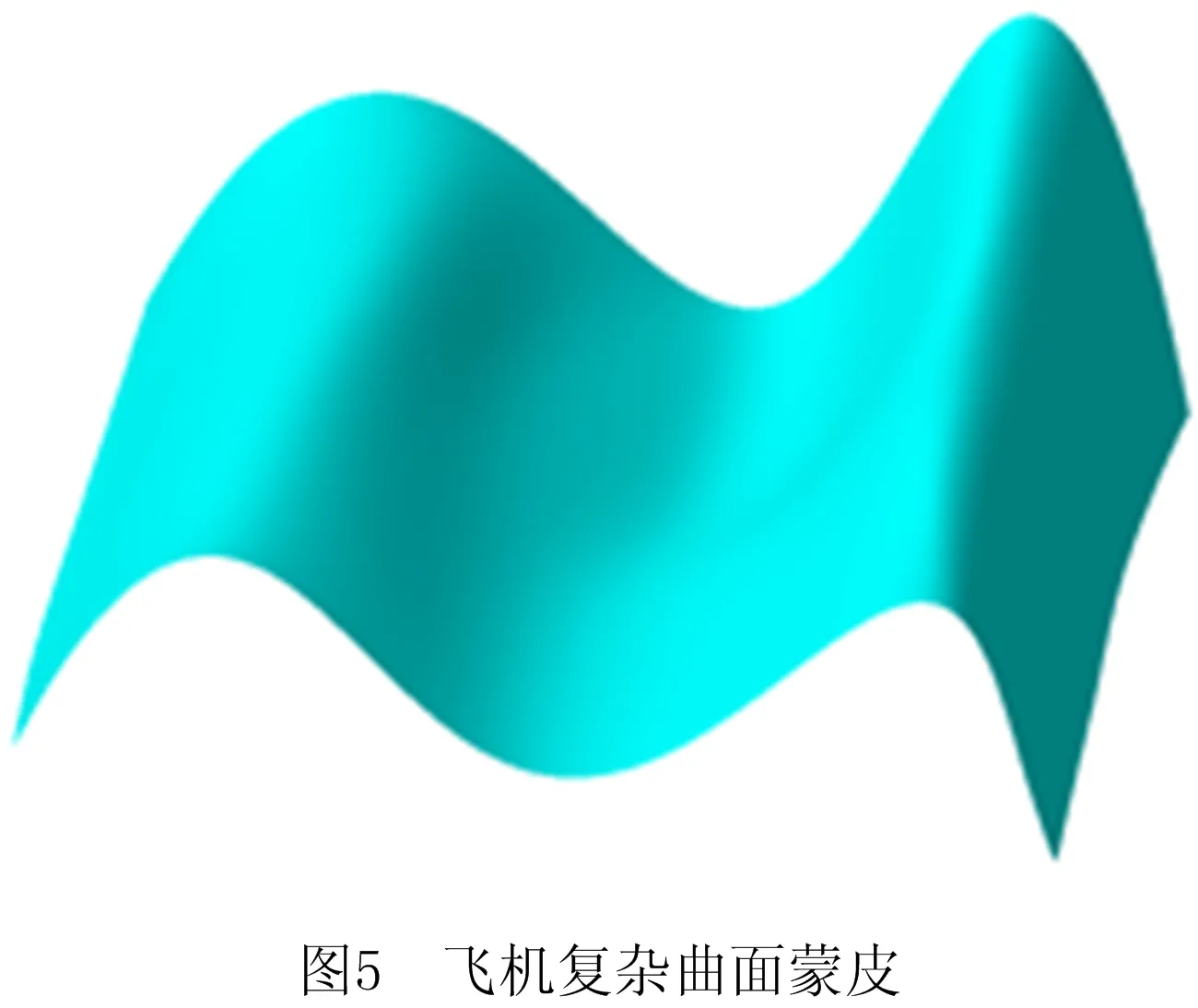
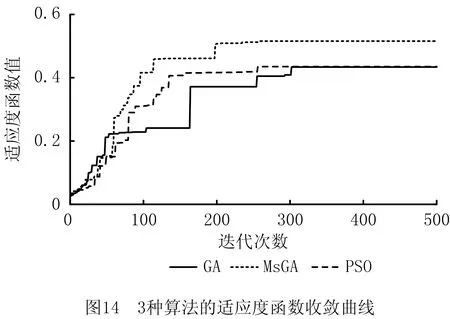
步骤6迭代结束判断。判断当前迭代次数k与最大迭代次数K的大小。若k (23) 为使机器人关节轨迹平缓、无突变,采用五次B样条进行关节轨迹插值: (24) 式中:u表示喷涂轨迹的节点,θ(u)表示各节点对应的关节角度,Di表示喷涂轨迹的控制顶点,Ni,5(u)表示样条基函数。由五次B样条基函数的性质可知,当u∈[ui,ui+1]时,至多存在6个非零的五次基函数Nj,5(u),故式(24)可转化为: (25) 利用喷涂机器人关节角速度、角加速度约束,构造满足式(23)的各特征点间的插值。 实例研究对象为如图5所示的飞机复杂曲面蒙皮,该曲面蒙皮由4条曲率陡峭、不规则、无节点的样条曲线拟合而成,U、V两个方向曲率连续变化。曲面最大长度为4 000 mm,最大宽度为3 000 mm,最大高度为1 490.97 mm。喷涂机器人型号为GSK-RB08。结合文献[15]中椭圆双β喷枪模型的喷涂轨迹最优间距1 000 mm,在复杂曲面上生成互相平行且间距相等的4条喷涂轨迹,并在每条轨迹上等间距离散出喷涂轨迹点。喷涂轨迹和喷涂轨迹点如图6和图7所示。 (1)夹角阈值确定 为确定阈值θmax,判定复杂曲面喷涂轨迹的转角,利用GSK-RB08机器人和Robotic toolbox工具箱测试机器人末端经过不同夹角θi时的运动参数。以机器人关节速度方差均值作为测试参数,量化机器人运行过程的速度波动。分别测试夹角等于0°、15°、30°、45°、60°、75°、90°时的速度方差,速度方差如图8所示。 由图8可知,当θi≤45°时,速度方差较小且增速平缓;当θi>45°时,速度方差迅速增大。因此,令θmax=45°。 (2)影响因素权重确定 基于专家给出的喷涂轨迹因素对比标度,构建层次判断矩阵: (3)喷涂轨迹点确定 为了选取足以表征喷涂轨迹的特征点,通常选取喷涂轨迹起止点、不同类型表面的连接点、加工表面曲率变化点、末端轨迹速度变化点等特殊位置,表现为喷涂轨迹对应函数的驻点、拐点及一阶导数不存在的点。依据以上条件可得到,如图9a所示为未优化的复杂曲面喷涂轨迹特征点q0~q23,如图9b所示为经MsGA优化后的复杂曲面喷涂轨迹特征点Q0~Q29。 (4)喷涂轨迹插值点确定 利用式(25)进行喷涂轨迹特征点五次B样条插值。如图10所示为Q0Q1的插值图,Q0Q1之间共有48个插值点。 (1)种群规模优化 以多因素模型对应的适应度函数值来判断种群规模对MsGA优化性能的影响,分别设Nmax=100、200、300,同时保留算法其余参数不变。设最大迭代次数K=500,子群个数Nmul=5,交叉尺度因子μcro=0.5,变异尺度因子μvar=0.5。不同种群规模MsGA的适应度函数如图11所示。由图11可知,不同种群规模MsGA的收敛代数虽然不同,但适应度函数最优值相当。 如表2所示,当Nmax=100时,算法的适应度函数值最大,达到0.515 7,略高于Nmax=200和Nmax=300时的0.515 3。同时,当Nmax=100时,适应度函数在321代趋于收敛,而后两者在377代及443代趋于收敛。3种算法耗时分别为59.647 s、137.118 s、222.123 s,算法耗时随着种群规模的增大而增大。因此,增大种群规模对MsGA的搜索性能无本质提升,Nmax=100时,算法已具备较高的收敛精度,且耗时更少。基于以上计算分析,设种群规模为100,在保证算法收敛精度的同时,减小算法的耗时。 表2 不同种群规模下MsGA性能对比 (2)机器人关节运动学性能优化 根据图8和图9,生成如图12和图13所示的机器人关节运动学参数曲线。对比图12和图13可得,相较于未优化的喷涂轨迹,经MsGA优化的机器人关节角速度和角加速度波动范围分别降低了21.3%和27.3%,能更好地保证机器人启停的稳定性,有效减小启停的冲击。 (3)喷涂轨迹多因素综合评价 分别采用MsGA、经典遗传算法(GA)及经典粒子群(Particle Swarm Optimization, PSO)算法求解机器人的喷涂轨迹。如图14所示为3种算法的适应度函数收敛曲线,如图15所示为3种算法求得的最优喷涂轨迹,如表4所示为喷涂轨迹的多因素综合评价。由图15和表4可看出,除干涉度一致为0外,相较于GA和PSO,MsGA优化喷涂轨迹的转折点数降低了33.3%,平均转折度提升了48.8%;轨迹总长分别降低了7.3%和2.2%,中位数长度分别提升了68.5%和65.0%;Ffea综合评价指标分别提升了26.2%和20.4%。综上所述,与经典的GA和PSO相比,MsGA收敛速度更快,收敛精度更高,利用MsGA能够得到量化评价指标更高的喷涂轨迹,此外,GA和PSO还拥有更强的全局和局部搜索能力。 表4 3种算法优化喷涂轨迹的多因素综合评价 针对复杂曲面喷涂轨迹的量化评价指标不够完善,本文定义了喷涂稳定性模型、喷涂效率模型、喷涂轨迹干涉模型,并以此构建了喷涂轨迹多因素模型,提出了基于多因素模型和多尺度遗传算法的复杂曲面喷涂轨迹综合优化方法。 针对机器人运动学性能指标研究,实例研究表明,通过与未经多尺度遗传算法优化的喷涂轨迹相比,利用多尺度遗传算法优化过喷涂轨迹,机器人关节角速度和角加速度波动范围分别降低了21.3%和27.3%,保证机器人启停的稳定性,有效减小启停的冲击。 为提升喷涂轨迹的多因素综合评价指标,解决遗传算法易出现早熟及搜索精度不高的难题,定义了多尺度遗传算法。以飞机复杂曲面蒙皮为对象进行实例研究,实例研究表明,与经典的遗传算法和粒子群算法相比,利用多尺度遗传算法进行喷涂轨迹优化,综合评价指标分别提升了26.2%和20.4%,可有效提高复杂曲面的喷涂质量。 在工程应用中,机器人喷涂轨迹质量影响因素众多,且影响因素的赋权对喷涂轨迹优化结果影响较大。在未来的研究中,可以进一步综合考虑喷涂轨迹质量多因素影响,完善喷涂轨迹多因素模型,并合理设置因素权重,以提升喷涂轨迹综合评价指标的准确性,使得对该问题的研究更加符合实际工况。3.3 喷涂轨迹插值
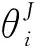
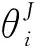

4 实例验证


4.1 模型参数确定




4.2 基于多尺度遗传算法的喷涂轨迹综合优化






5 结束语

