基于FSDD和MAC的复杂工况滚动轴承在线故障诊断方法*

孙万峰,王 禹,孙 宇,武 凯

(南京理工大学 机械工程学院,江苏 南京 210094)

0 引 言

环模制粒机是生物质能源和饲料工业等领域的关键设备[1],其核心零件需在高温、高湿条件下长时间连续运行,极易发生滚动轴承故障,造成不规律的振动和噪声,甚至会引起周围设备共振,严重影响生产安全,污染工作环境。

环模制粒机包含多组滚动轴承,且轴承工况复杂。该机的实际运行状况表明,不同位置的轴承均可能发生故障。

在实际工程中,针对环模制粒机的轴承故障,往往采用停机拆解、逐一检测的方法来判断具体的故障位置。该方法的操作复杂,且必须停止整条生产线,影响生产效率。因此,有必要针对环模制粒机滚动轴承在线故障诊断方法进行研究。

滚动轴承是重要的基础零件,广泛应用于各种旋转机械中。其运行状态对整个机械设备的运行状态有直接影响[2]。滚动轴承被安装在机械设备的旋转部位,难以观察其健康状态,且拆装难度较大。

目前,滚动轴承故障诊断的主流方法是依据振动信号处理的故障诊断方法,对于故障特征频率识别,一般是将时域信号转换到频域上进行分析。当旋转机械系统中有随机激励输入时,振动信号将含有大量白噪声。此时,使用一般的频谱分析,例如傅里叶变换等,难以识别故障的特征频率。

频域分解法(frequency domain decomposition,FDD)是多输入多输出(multiple-input multiple-output,MIMO)的频域分析方法[3],是常用的运行模态分析(operational modal analysis,OMA)方法之一[4]。

BRINCKER R等人[5]在复模态指示函数的基础上,提出了第一代FDD方法,FDD能够用于识别模态频率和振型;但FDD方法存在无法识别模态阻尼的缺点。为了消除这一缺点,BRINCKER R等人[6]在FDD的基础上,提出了第二代FDD法—增强频域分解(enhanced frequency domain decomposition,EFDD),EFDD不仅能用于估计模态频率和振型,还可以用于估计阻尼比;但是,EFDD在采用逆傅里叶变换计算相应单自由度系统的近似相关函数时,使用了截断数据(仅使用峰值附近的数据),EFDD可能会在阻尼估计中引入偏差误差;此外,其在处理密集模态时,经常会出现拍频现象。为了消除这些缺点,王彤等人[7]提出了第三代FDD法—频率空间域分解,模态频率与阻尼在频域内从增强功率谱(enhanced power spectral density,EPSD)中直接识别,无需对奇异值曲线进行逆傅里叶变换,因此,可得到更为准确的识别结果;但是,由于旋转机械的振动中存在旋转轴产生的谐波,使FDD类方法用于进行模态识别时产生偏差。因此,FDD类方法无法直接应用于旋转机械的故障诊断。

为了解决这一问题,STORTI G C等人[8]采用振动信号质量评价、去谐波等预处理方法,将FDD类方法用于旋转机械的模态识别;但是,单一的FSDD方法难以应用于滚动轴承的故障诊断上。需要对FSDD识别出的模态参数更进一步分析,才能提取出滚动轴承的故障。

为了解决这一问题,PACHECO C J等人[9]采用FDD结合模态形状差法的方法,对风力发电机叶片的故障进行了诊断;但模态形状差法是计算每个节点处的模态形状差,需要的测点多,难以应用于轴承等小型零件的故障诊断上。

模态保证准则是一个模态指标,旨在确定其计算中使用的振型是否对应于同一模态[10]。模态保证准则类参数均是基于相关原理的损伤评判方法,应用于不同系统识别程序之间的模态估计比较[9]、损伤检测[10]以及其他许多涉及模态向量的比较。MAC分析需基于FSDD等方法识别出的模态参数,才能实现故障提取。

在现有研究的基础上,笔者以存在异常振动和噪声故障的环模制粒机为对象,研究存在随机激励的复杂工况下滚动轴承的故障诊断。

笔者分别对空载运行、正常运行和重载运行3个工况下环模制粒机的振动进行测量,利用FSDD识别出可能发生故障的特征频率,最后通过MAC识别出发生故障的特征频率,与滚动轴承的故障特征频率进行比较,完成对滚动轴承的故障诊断。

1 滚动轴承故障诊断方法

1.1 滚动轴承特征频率

当滚动轴承在运行过程中发生故障时,出现故障的位置因为相互冲击而产生异常振动,会引起具有特定故障频率的振动峰值[11]。因此,可以根据该频率峰值的出现和变化对轴承损伤状态进行检测。

轴承内圈、外圈、保持架和滚动体的故障特征频率计算公式,分述如下[12]:

滚动轴承内圈故障特征频率计算公式如下式所示:

(1)

式中:fo—轴承外圈转动频率,Hz;fi—轴承内圈转动频率,Hz;Z—滚珠个数,个;d—滚动体直径,mm;D—轴承节径,mm;α—体接触角,°。

滚动轴承内圈故障特征频率计算公式如下式所示:

(2)

滚动轴承保持架故障特征频率计算公式如下式所示:

(3)

滚动轴承滚子故障特征频率计算公式如下式所示:

(4)

1.2 RMS分析

RMS是工程应用中是最常采用的时域统计指标之一[13]。对于总体样本点为N的离散时域信号x(n),其RMS如下式所示:

(5)

由于RMS是对样本总体N的平均,因此,能较好地反映振动信号的总体动态信息,常用来判断机械设备的整体运转状态[14]。

1.3 频域空间分解法

1.3.1 频域分解法

频域分解法是基于随机过程输入和输出的功率谱密度(power spectral density, PSD),其关系公式如下式所示[15]:

Gyy(ω)=H(ω)Gxx(ω)H(ω)H

(6)

式中:Gxx(ω),Gyy(ω)—输入、输出PSD矩阵;H(ω)—频率响应函数矩阵。

FDD技术的关键是对以离散频率ω=ωk估计的输出PSD进行类似于式(6)的因式分解,对输出功率谱密度矩阵Gyy(ω)进行奇异值分解,如下式所示:

Gyy(ω)=USVH

(7)

式中:U,V—奇异值向量组成的酉矩阵;S—奇异值构成的实数对角矩阵。

在第m阶固有频率ωmd附近,对Gyy(ω)的估计如下式所示:

ΔGyy(ωk)≈s1(ωk)u1(ωk)v1(ωk)

(8)

式中:s1—第一奇异值;u1,v1—U、V的第一列奇异向量。

在固有频率处(ωk=ωmd),达到最大值的第一个主值描述了模态坐标ωmd。相应的主向量u1(ωmd)是对第m个振型的估计,因此,φm=u1(ωmd)具有归一化。

1.3.2 频域空间分解

频域空间分解法与实验室模态分析方法中复模态指示函数识别法类似[16],其核心思想是对固有频率ωdm附近的功率谱矩阵Gyy(ω)进行奇异值分解,将其转换为单自由度系统响应的功率谱(即增强功率谱),然后通过单自由度拟合方法进行模态参数识别。

其识别过程分两步:

(1)增强功率谱

响应信号的功率谱矩阵Gyy(ω)在第m阶特征频率ωmd附近进行奇异值分解,如式(7)所示。分别取U、V的第一列奇异向量u1、v1计算增强功率谱ΔGen,如下式所示:

(9)

(2)模态参数

在特征频率附近,ΔGen可以近似地表示为[17]:

(10)

式中:cm—系数;λm—第m阶模态对应的极点。

其中:

λm=-σm+iωdm

(11)

采用特征频率附近所有频率点,对式(10)进行最小二乘法求解,可以得到模态参数:

(12)

式中:fm—第m阶模态特征频率,Hz;ξm—第m阶模态的阻尼系数,%。

1.4 基于模态保证准则损伤检测方法

模态保证准则是利用模态相关的原理来诊断结构是否受到损伤,如下式所示[9]:

(13)

式中:φ—模态振型;上标u,d—健康状态、损伤状态;下标i,j—第i阶和第j阶模态。

MAC值的范围为[0,1]:当MAC值趋近于1时,表示结构健康;当MAC值趋近于0时,表示结构损伤程度严重。

MAC利用振型的正交特性,对两个不同振型进行比较,在模态试验中,常用于检验测量模态振型的正交性。

MAC也指损伤前后模态振型的关联系数,在实际应用时,当MAC大于0.9时,两模态振型相关联;小于0.05时,两模态振型无关。

基于FSDD和MAC的滚动轴承在线故障诊断方法流程,如图1所示。

图1 基于FSDD和MAC的滚动轴承在线故障诊断方法流程

2 振动信号在线测量

按照上述的故障诊断方法,首先,需针对设备的振动进行数据采集。

以一台存在故障的K15环模制粒机为对象进行试验。该环模制粒机在负载运行时,出现了不明原因的振动,需要检测其齿轮箱及滚动轴承是否发生故障及故障位置。

笔者使用加速度传感器(PCB,50 g)配合振动信号采集卡(NI 9232)来检测机身振动。K15环模制粒机的主要滚动轴承有3个,轴承的型号分别为NJ226ECP、SKF 23948CC/W33和SKF 24024CC/W33。

笔者对K15环模制粒机的齿轮箱部分进行振动加速度在线测量。试验在饲料加工厂进行,环模制粒机的工作环境复杂。

K15环模制粒机轴承机构参数如表1所示。

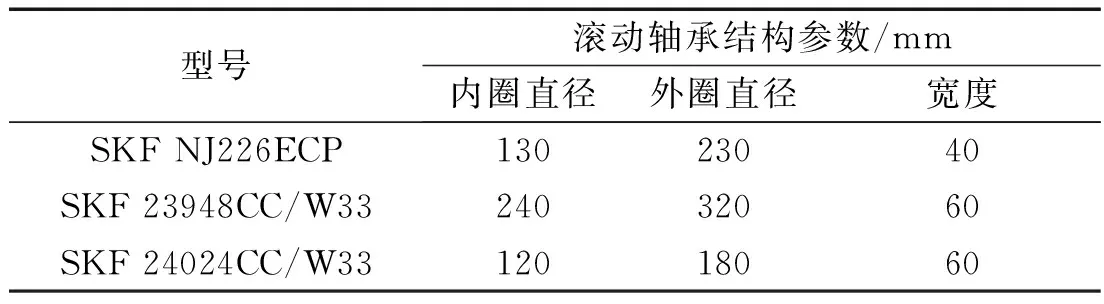
表1 K15环模制粒机轴承结构参数

K15环模制粒机运行过程中,电机转速固定为1 480 r/min,制粒机主轴转速为272 r/min。笔者分别在空载运行、正常运行和重载运行3种工况下对环模制粒机的振动和负载进行测量。

笔者通过对电机轴扭矩的测量,获得了不同工况电机轴扭矩,如表2所示。

表2 不同工况电机轴扭矩

3个工况中,滚动轴承承受不同的载荷:空载运行时最小,重载运行时最大。环模制粒机空载运行时,不加入饲料原料进行饲料制粒;环模制粒机正常运行时,加入饲料原料(粉料)进行饲料制粒;环模制粒机重载运行时,加入预先制粒完成的颗粒饲料进行制粒。

试验过程中,环模制粒机空载运行时,没有明显噪声;正常运行时,环模制粒机出现噪声;当环模制粒机重载运行时,出现明显噪声。

K15环模制粒机及振动测点布置图如图2所示。

图2 K15环模制粒机及振动测点布置图

图2中:1#、2#和3#加速度传感器分别检测压辊轴轴向、竖直方向和水平方向的振动;4#和5#为三轴加速度传感器,可以检测齿轮箱下方和上方两个位置的振动,振动测量过程中将5#测点的传感器移到5′#测点,对压辊轴末端的振动进行测量。

重载运行时振动加速度信号如图3所示。

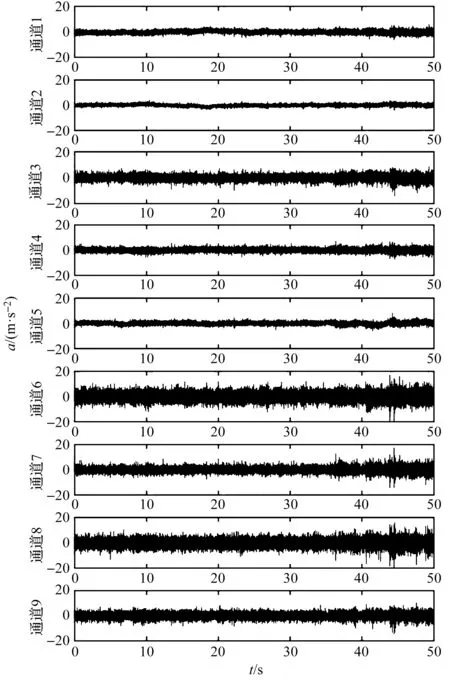
图3 重载运行时振动加速度信号

3 数据分析与故障诊断

按照上述基于FSDD和MAC的滚动轴承在线故障诊断方法,需要对振动信号进行RMS分析、FSDD分析及MAC分析,其具体流程如图1所示。

3.1 RMS分析

笔者分别计算3个工况下各个测点振动信号的RMS均值,得到3个工况下的RMS分析结果,3个工况各测点的RMS均值如图4所示。

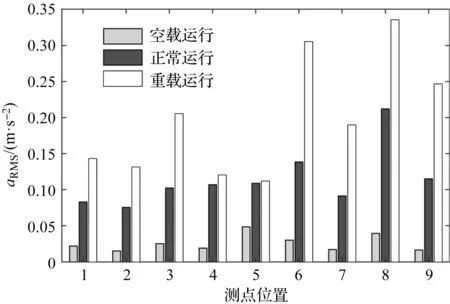
图4 3个工况各测点的RMS均值1,2,3—1#、2#、3#测点测量振动信号的RMS均值;4,5,6—4#测点测得振动信号的RMS均值;7,8,9—5′#测点测得振动信号的RMS均值

由图4可知:重载运行时,由于环模制粒机的零部件受到的载荷较大,发生磨损或损伤,其RMS均值明显大于另外两个工况。

此外,齿轮箱内部各零部件的振动信号都会通过轴、轴承等零部件最后传递到轴承座[18]。从故障诊断的角度考虑,5′#测点位于压辊轴末端,其对齿轮箱损伤及故障信号反应更加敏感。这也是导致5′#测点的重载运行时RMS明显增大。

重载运行时,工况相对恶劣,此时故障冲击产生的能量相对较大,故障特征明显且对损伤的变化较为敏感。故笔者对重载运行时测得的振动信号进行FSDD分析,提取出环模制粒机的故障特征频率。同时,与空载运行和正常运行时进行对比,通过MAC分析识别出环模制粒机的损伤部位。

3.2 频域空间分解

频域空间分解法属于MIMO技术,可以将多个通道的振动信号作为输入进行分析,输出多个模态[19]。根据RMS分析的结果,对环模制粒机重载运行时测得的振动信号进行频域空间分解法分析。

响应谱矩阵的奇异值曲线,如图5所示。

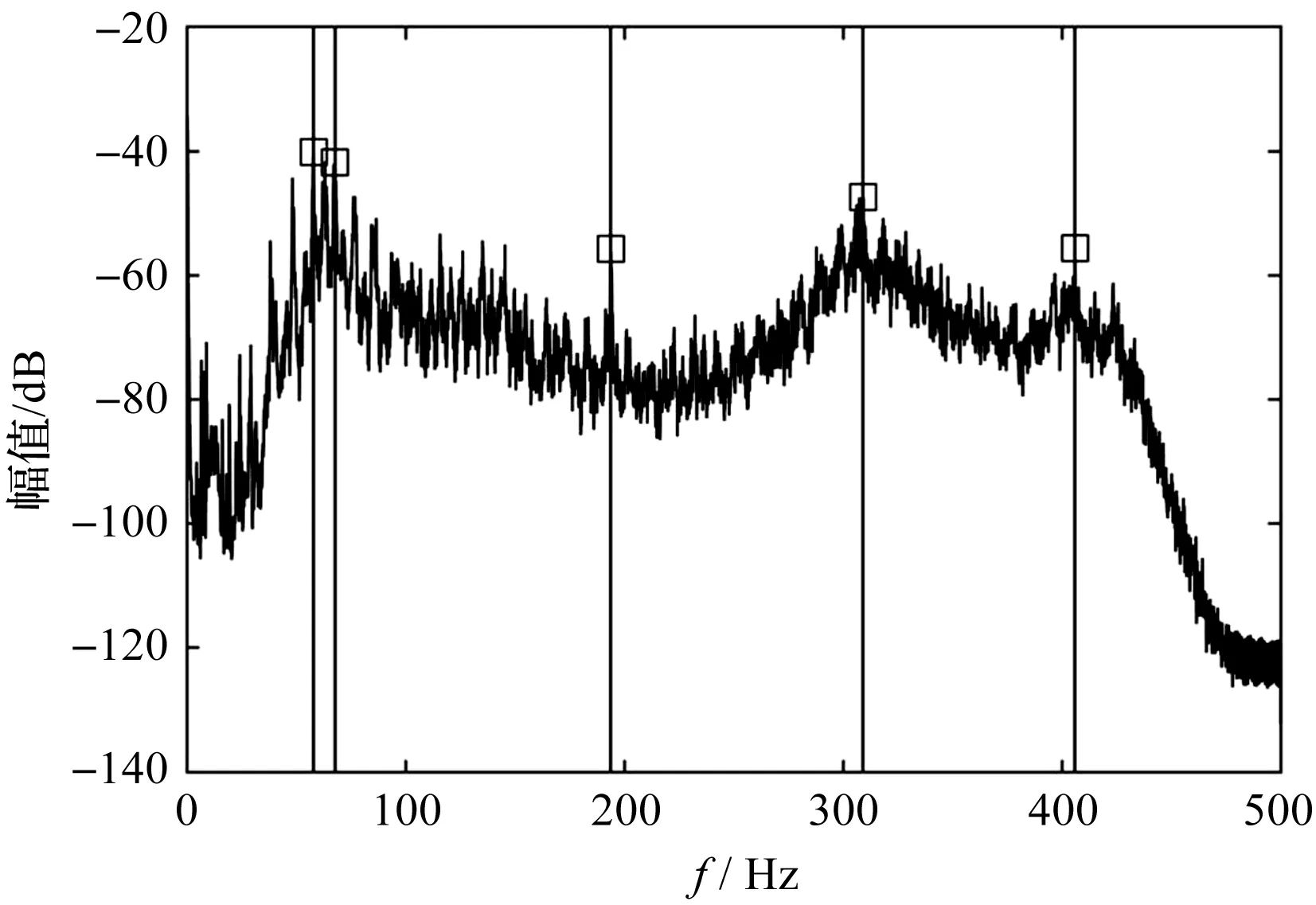
图5 响应谱矩阵的奇异值曲线

笔者以重载运行时5个测点测得9个通道的振动信号作为FDD法的输入,计算出奇异值。通过PickPeak法从主值贡献最大的第一奇异值中识别了出5个模态,如图5所示。

为了判断识别出的模态是否独立,笔者对上述5个模态的振型进行模态保证准则分析。计算各个模态之间的MAC值,将MAC值绘制成MAC矩阵图[20]。

各模态之间的MAC图如图6所示。

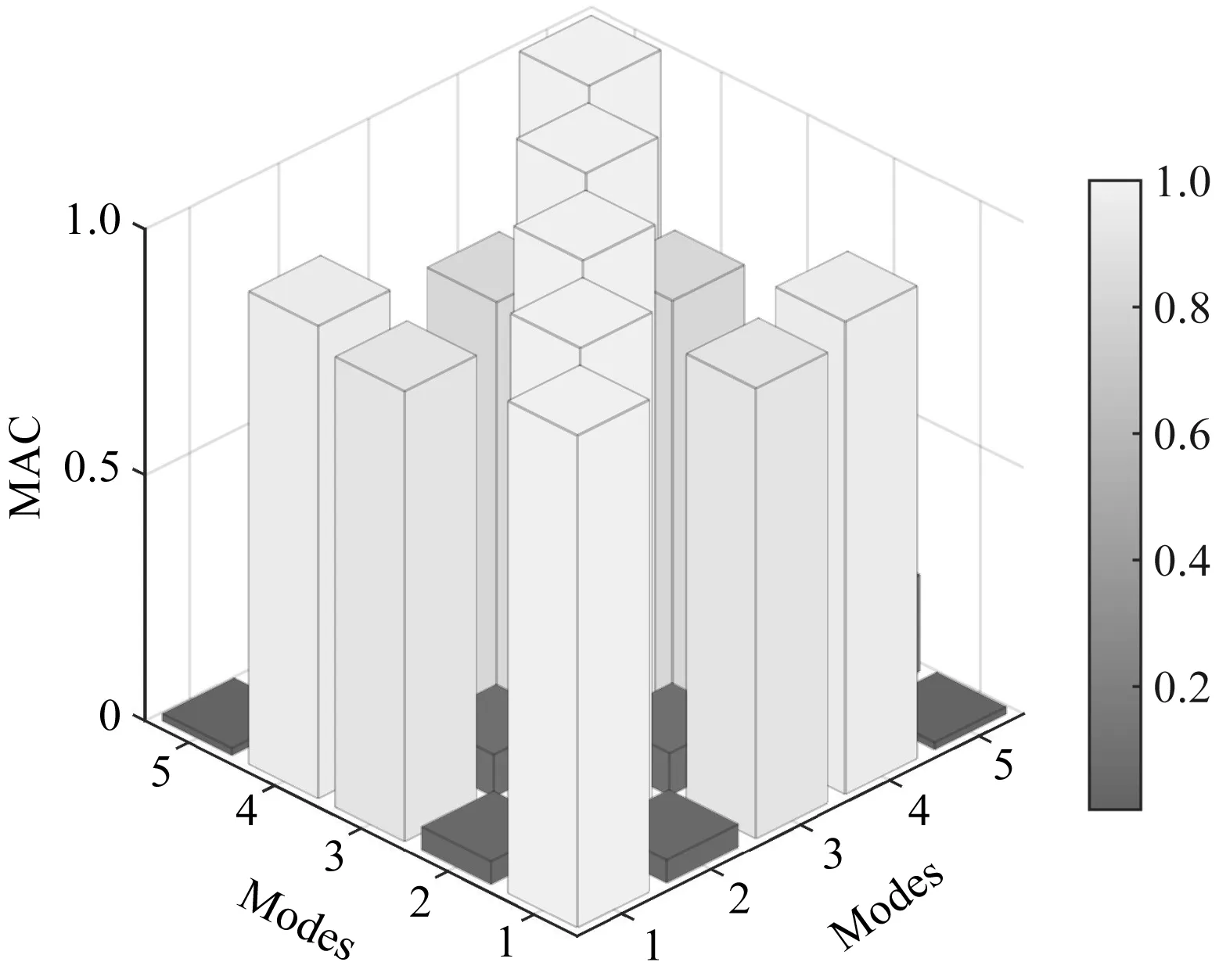
图6 各模态之间的MAC图

从图6中可以看出:模态1和模态3、模态1和模态4、模态3和模态4之间的MAC接近于1,表明模态3、4与模态1相关联,故不是环模制粒机独立的模态。

增强功率谱及其拟合曲线(模态1)如图7所示。

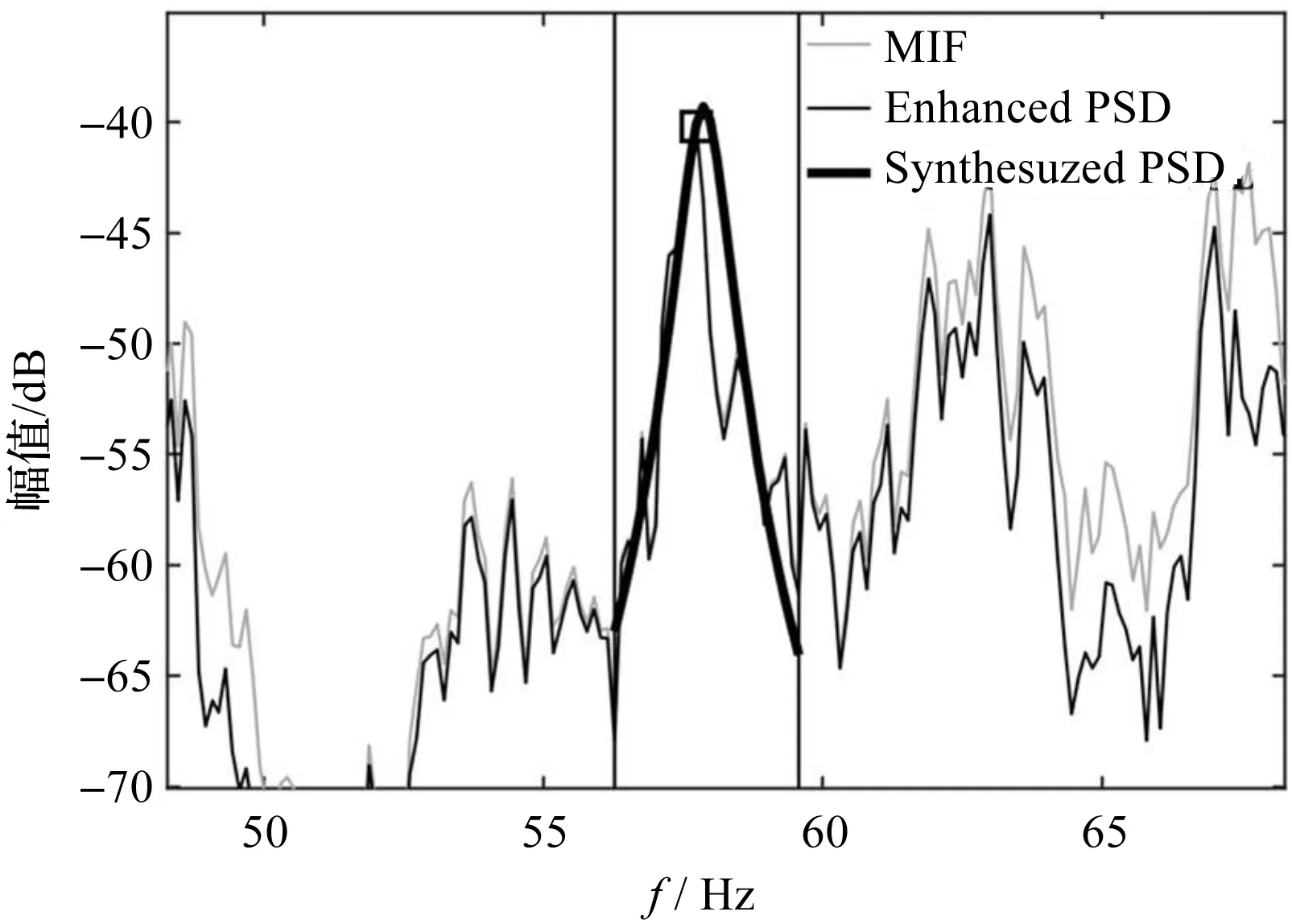
图7 增强功率谱及其拟合曲线(模态1)

增强功率谱及其拟合曲线(模态2)如图8所示。

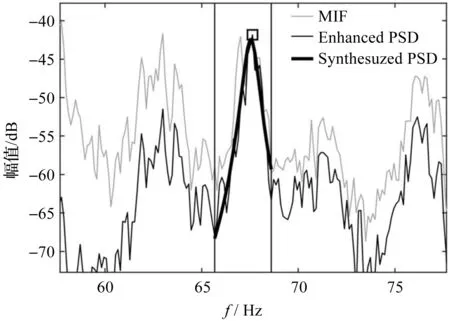
图8 增强功率谱及其拟合曲线(模态2)

增强功率谱及其拟合曲线(模态3)如图9所示。

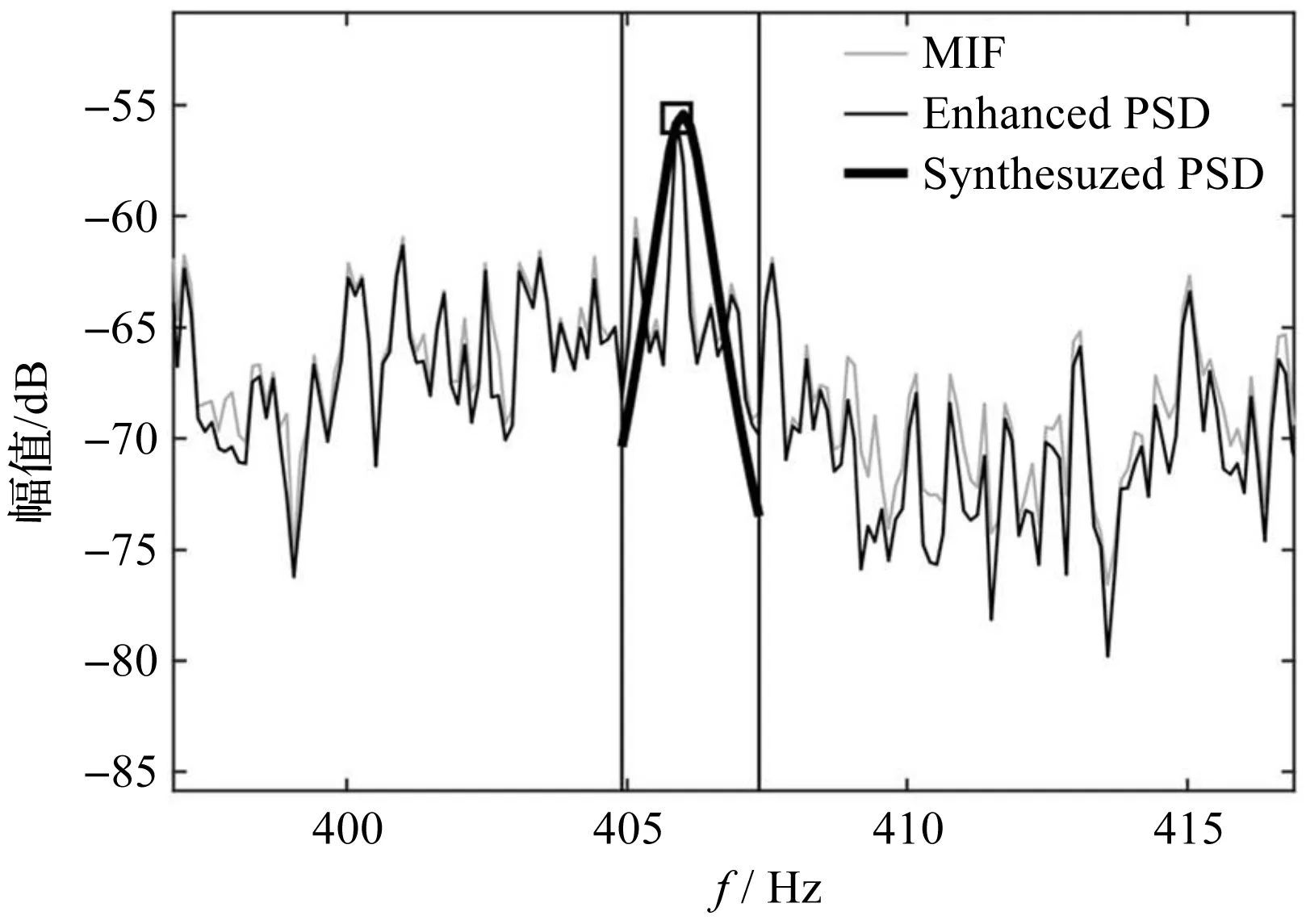
图9 增强功率谱及其拟合曲线(模态3)

图(7～9)显示了FSDD分析的结果,其中:两条竖线为频率的拟合范围,其中包含了30根谱线。

通过最小二乘法拟合,笔者获得了模态附近的拟合曲线,根据式(12)计算出其对应的模态频率和阻尼系数[21]。

FSDD识别的模态如表3所示。

表3 FSDD识别的模态

3.3 基于MAC的损伤识别

空载运行时,环模制粒机的运动部件没有受到除自重外其他载荷。此时,相对其他工况,轴承等零部件受到的载荷与冲击最小,零部件的损伤和损坏对特征频率的影响最小。因此,可以近似认为空载运行时,环模制粒机的振动状态是健康状态下的振动状态。

为了计算不同工况之间的MAC值,需要对另外两个工况进行FSDD分析。

3个工况的响应谱矩阵的奇异值曲线如图10所示。

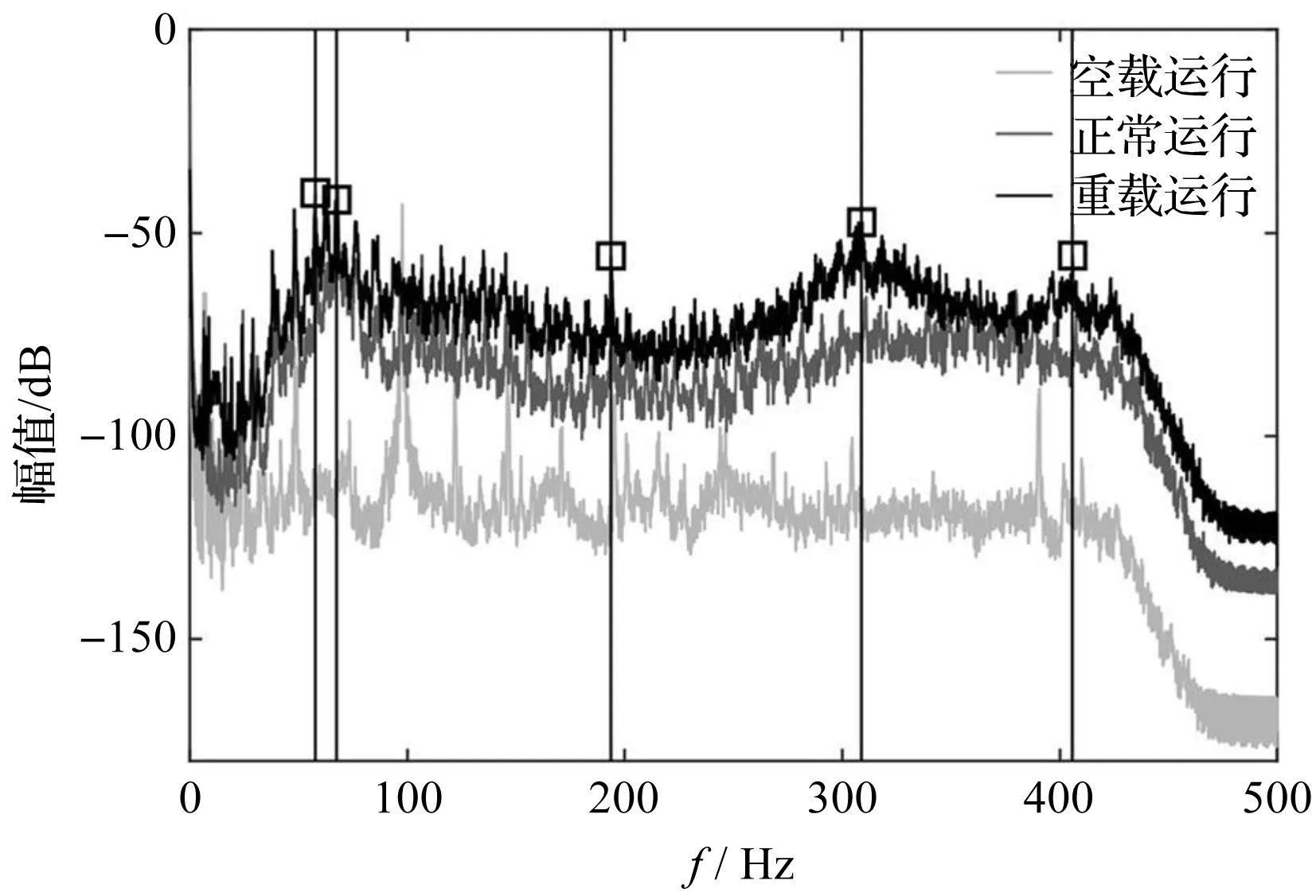
图10 3个工况的响应谱矩阵的奇异值曲线

笔者以环模制粒机空载运行的振动状态为基准,计算另外两个工况下3个模态与空载运行时的MAC值。

3个工况各模态的MAC值如表4所示。

表4 3个工况各模态的MAC值

其中,空载运行-正常运行、空载运行-重载运行的第一阶模态MAC值均小于0.05,根据MAC判断:当MAC小于0.05时,表示结构出现损伤。表明第1阶模态为故障特征频率,且该故障特征频率所代表的结构损伤较为严重[22]。

故障特征频率估计误差计算公式为:

(14)

式中:E—误差,%;fFSDD—FSDD估计的模态频率,Hz;fr—滚动轴承故障特征频率,Hz。

通过FSDD分析,获得的估计特征频率为57.83 Hz,估计阻尼比为0.81%。故障特征频率的估计误差通过式(14)进行计算[23],其估计误差为1.96%。

3.4 滚动轴承故障分析

根据上述分析可知,估计特征频率为57.83 Hz。为了确定故障位置,根据滚动轴承结构参数计算出故障特征频率。

滚动轴承故障特征频率如表5所示。

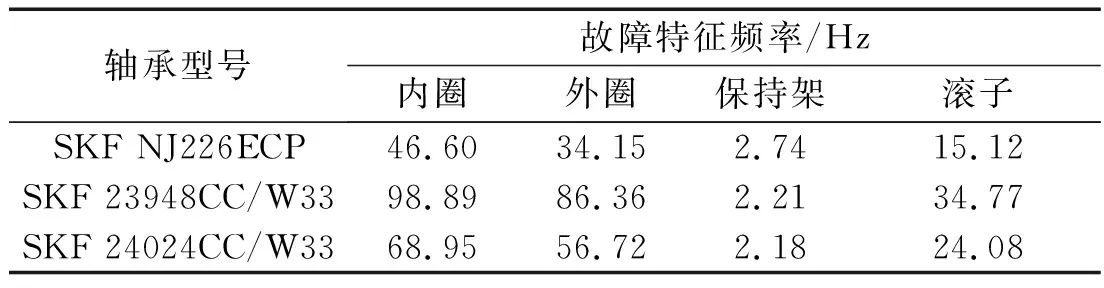
表5 滚动轴承故障特征频率

根据表5,与故障特征频率相吻合的只有SKF 24024CC/W33滚动轴承。据此可以判断压辊轴与主轴之间的滚动轴承SKF 24024CC/W33出现故障,且故障产生在轴承外圈。该轴承安装在环模制粒机压辊轴与主轴之间,承受的载荷较大,发生损伤或损坏的几率较大。

根据上述分析结论,笔者更换了压辊轴与主轴之间的滚动轴承,环模制粒机可正常运行,不再出现异常振动和噪声。

4 结束语

针对复杂工况下环模制粒机滚动轴承故障无法在线诊断的问题,笔者提出了一种基于频域空间分解和模态保证准则的滚动轴承在线故障诊断方法,并以出现不明振动故障的K15环模制粒机为对象,进行了轴承故障诊断实验。

研究结果表明:

(1)与正常工况和重载工况相比,空载工况下机器的振动可以忽略,可以作为健康状态进行故障诊断;

(2)FSDD可以用于机械系统模态的提取,结合MAC可以准确地识别出系统的独立模态,避免了噪声等对模态识别的影响;

(3)比较了空载工况与重载工况之间的MAC,该方法提高了故障识别的准确性,在复杂工况下轴承的故障特征频率为57.83 Hz。

在后续的研究工作中,笔者将针对OMA在机械故障诊断方面应用进行研究,以进一步提高复杂工况下该方法的故障诊断性能和效率。