基于SNN-LSTM的小样本数据下轴承故障诊断方法*

吕云开,武 兵,2*,李聪明,2

(1.太原理工大学 机械与运载工程学院,山西 太原 030024;2.太原理工大学 新型传感器与智能控制教育部重点实验室,山西 太原 030024)

0 引 言

当前,故障诊断技术广泛应用于汽车、航空航天、电气、制造业等多个领域。

在使用滚动轴承的机械装备中,大约有30%的机械故障是由滚动轴承的损坏引起的,可见滚动轴承的工作状态在很大程度上影响着整个机械设备的运行状态。因此,轴承故障诊断技术的研究一直是机械故障诊断中的重中之重。

目前,故障诊断技术主要是基于信号处理的方法以及基于人工智能的方法[1]。其中,基于信号处理的方法是利用信号分析技术来分析时域、频域以及时频域的特征。

夏理健等人[2]对滚动轴承振动信号进行完备总体经验模态分解后,选择固有模态函数分量,求出了其散布熵和Hjorth参数,最后将其输入到支持向量机中,实现了对轴承故障的分类诊断。彭程程[3]通过构建轴承振动信号的二阶频率变化模型,以及观察短时傅里叶变换时频图,进行了轴承的故障诊断。LI W等人[4]利用数学形态学中的开运算、闭运算,对信号进行了滤波、去噪,利用香农熵的定义获得了归一化形态谱熵,采用改进的准解析复小波变换分解,实现了对轴承的故障诊断。NI Q等人[5]采用广义高斯循环分析模型和广义高斯分析模型,并结合特定的统计阈值,近似确定了模态数,然后定义了故障特征幅值比,确定了最优带宽控制参数,并将信号进行了变分模态分解,最后进行了轴承的故障诊断。

近年来,基于深度学习的轴承故障诊断方法备受人们的关注,因为该方法可以克服人工分析方法相对耗时、主观的缺点,具有能够自适应地从振动信号中提取故障特征的能力。FANG Q等人[6]采用3层卷积神经网络与门控循环单元相结合来提取特征,并且引入自注意力机制,并输入到自归一化网络,对轴承进行了故障诊断。贾峰等人[7]采用深度卷积神经网络,提取了轴承的样本特征,然后采用加权领域鉴别器,解决了“目标域中出现额外故障样本会影响轴承故障诊断精度”的问题。LING Hai-tao等人[8]首先通过连续小波变换生成了时频图,之后采用卷积神经网络以及双向长短时记忆网络,提取了故障特征,最后将其输入到数字胶囊网络中,从而完成了对轴承故障的分类诊断。

为了实现以上深度学习的方法,需要用到大量的、有标注的训练样本,而在小样本数据下,采用这些方法会产生模型欠拟合问题,同时采用该方法获得的分类准确率也较低。

为了解决以上问题,笔者提出一种结合孪生神经网络与长短时记忆网络的轴承故障诊断方法,即以一对带有正负标签的原始振动信号样本作为诊断方法的输入,使用参数共享的卷积层、池化层以及长短时记忆网络层,提取输入样本对的特征,通过计算二者之间的曼哈顿距离,判断输入样本对的相似度,最后在小样本数据下,实现对不同状态轴承的分类诊断。

1 SNN-LSTM故障诊断模型

1.1 卷积神经网络

卷积神经网络(convolutional neural networks,CNN)[9]具有强大的特征提取能力,是深度学习中的代表网络。

一般情况下,卷积神经网络主要由卷积层、池化层、全连接层等组成。卷积层是采用一定数量大小的卷积核,对上一层输出的样本进行卷积运算,加上偏置向量,通过激活函数的激活,然后作为下一层的输入。

卷积核数量的多少对应着下一层的深度,卷积的数学公式如下所示:

Xl=f(Wl*X(l-1)+bl)

(1)

式中:X(l-1)—第l-1层的输入;Wl—第l层里卷积核的权重矩阵;bl—偏置向量;f()—第l层的激活函数;Xl—经过卷积计算后第l层的输出,也是下一层的输入。

经过卷积运算后,需要用到非线性激活函数进行非线性变换,来增强模型的拟合能力。常见的激活函数有ReLU、sigmoid、SoftMax等,其数学公式分别如下所示:

(2)

(3)

(4)

在上式中:ReLU激活函数由于其简单的运算被用于卷积层、池化层等进行激活,可以加速模型的收敛速度。

sigmoid激活函数在输入较大的情况下会出现软饱和性,从而导致梯度无法向后传递、更新参数,进而导致梯度消失。因此,sigmoid激活函数一般不作为卷积层的激活函数,通常在二分类问题中作为输出层的激活函数来输出概率。

SoftMax激活函数则常用于多分类问题中,作为输出层的激活函数来输出概率。

经过卷积层后的特征维度一般比较大,使用池化层可以有效地降低特征维度,防止由于模型参数过多从而产生的过拟合问题。

池化层的运算如下所示:

O(l+1)=Fpool(Xl)

(5)

式中:Xl—第l层经过卷积层进行激活后的输出;O(l+1)—经过池化层后的输出。

常用的池化层有最大池化层以及平均池化层,笔者所采用的是最大池化层。

1.2 孪生神经网络

孪生神经网络是为了解决小样本学习问题[10]而提出的一种网络结构。

现阶段,孪生神经网络主要用于食品识别、语音识别、人脸识别、表情识别等领域[11]。而将孪生神经网络用于轴承故障诊断的研究目前还比较少。

孪生神经网络的结构如图1所示。

图1 孪生神经网络原理图

这是一种可以学习2个样本之间相似度的网络。输入的样本是一个样本对(x1,x2,y)。其中:y=1表示2个样本是来自同一类;y=0表示2个样本来自不同类。

将一对样本输入到参数共享的两个神经网络中,通过网络输出得到fw(x1),fw(x2),之后将其输入到能量函数E中,表达式如下所示:

Ew(x1,x2)=‖fw(x1)-fw(x2)‖

(6)

式中:Ew(x1,x2)—两个输入之间的相似度。

能量函数E可以是任意相似性度量函数,常见的有:曼哈顿距离、欧氏距离、闵可夫斯基距离、余弦相似度等。其中,欧式距离等既要涉及加减运算,还需要进行开方运算,从而容易导致计算相对麻烦。

而曼哈顿距离只涉及加减运算,并且可以消除开方过程中取近似值带来的误差。因此,此处笔者所用的是曼哈顿距离。

曼哈顿距离表达式如下所示:

df(x1,x2)=|fw(x1)-fw(x2)|

(7)

式中:输出—fw(x1),fw(x2)两个向量之间的曼哈顿距离。

孪生神经网络的输出是样本对的相似性,也是样本对来自相同类的概率,其公式如下所示:

P(x1,x2)=sigm(FC(df(x1,x2)))

(8)

式中:FC—全连接层;sigm—sigmoid激活函数。

孪生神经网络中,常见的损失函数为二元交叉熵损失函数以及对比损失函数[12],二者单次训练的损失函数公式分别如下所示:

Loss1(P(x1,x2),y)=-ylog(P(x1,x2))-(1-y)log(1-P(x1,x2))

(9)

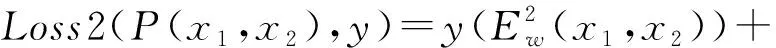
(10)

式中:P(x1,x2)—一对样本的预测相似度;y—真实标签0或1;Ew(x1,x2)—能量函数;margin—超参数阈值:当输入的两个样本不相似、二者距离大于这个阈值时损失为零。

由于对比损失函数需要调整超参数,此处笔者选用二元交叉熵损失函数。

最后,通过相似度的分析[13],就可以判断测试样本应该属于哪一类。

1.3 长短时记忆网络

长短时记忆网络[14]是为了改善在循环神经网络中,长序列样本在训练过程中存在的梯度消失、梯度爆炸等问题,而提出的改进网络。

长短时记忆网络的核心思想是,可以通过遗忘不同程度的长时记忆,并加上此刻产生的短时记忆,从而来控制此时刻经过长短时记忆网络所产生的输出值。

长短时记忆网络主要由遗忘门、输入门和输出门来控制其输出值。

遗忘门用来记录长时记忆的遗忘程度,决定上一时刻的记忆细胞状态有多少保留到此刻的记忆细胞状态。

遗忘门的公式如下所示:

ft=σ(Wf·[ht-1,xt]+bf)

(11)

式中:ht-1—上一时刻的输出;xt—当前时刻的输入;Wf—遗忘门的权重矩阵;bf—偏置向量;σ—sigmoid激活函数;ft—遗忘门的输出。

输入门用来记录当前时刻的短时记忆,决定这一时刻有多少信息被保留。

输入门公式如下所示:

it=σ(Wi·[ht-1,xt]+bi)

(12)

(13)

(14)

输出门用来作为长短时记忆网络最后的输出,其公式如下所示。

ot=σ(Wo·[ht-1,xt]+bo)

(15)

ht=ot·tanh(ct)

(16)

式中:Wo—输出门的权重矩阵;bo—输出门的偏置向量;ht—最后的输出,由输出门的输出和该时刻的记忆细胞状态决定。

1.4 SNN-LSTM

最终,笔者所确定的网络结构如图2所示。

图2 SNN-LSTM网络原理图

网络的输入是原始振动信号的一对样本,标签为0或1。笔者采用比较二者相似度的方法来扩充训练样本个数,使其更适用于小样本数据。

笔者通过共享提取样本对特征的网络参数来完成孪生神经网络的搭建,经过卷积层、池化层提取特征后,用长短时记忆网络层进一步提取有关时间序列的特征,最后进行全连接,并计算二者曼哈顿距离,从而输出0到1之间的值,利用真实标签和二元交叉熵损失函数,进行梯度反向传播,更新网络参数。

SNN-LSTM网络主要参数如表1所示。

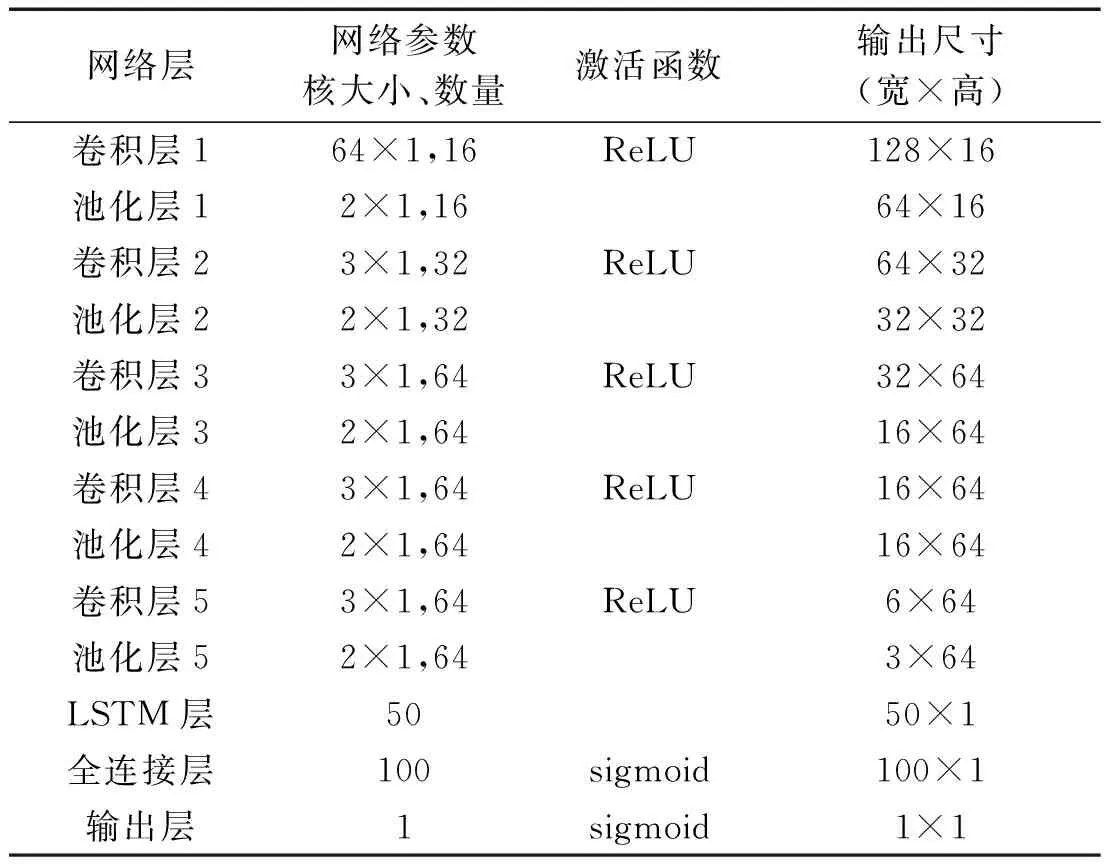
表1 SNN-LSTM网络主要参数

SNN-LSTM采取小而深的网络结构,第一层卷积核过小,容易受到高频噪声的干扰;而过大,则容易丢失局部特征。因此,笔者认为采用中等大小的卷积核比较合适[15]。

基于SNN-LSTM的故障诊断模型训练以及测试步骤,如图3所示。

图3 SNN-LSTM网络故障诊断模型流程图

基于SNN-LSTM的故障诊断具体步骤如下:

(1)划分数据集。对采集到的原始振动信号进行划分,划分出训练集与测试集;

(2)模型训练。每次在训练集中抽取两个样本,形成样本对输入到SNN-LSTM网络中,通过损失函数进行梯度下降,反向传播到网络中,从而更新网络参数。当模型训练到一定次数或者收敛时,停止训练,保存模型;

(3)测试样本故障分类。在测试集中随机选择一个样本作为测试样本。

在训练集中,每一类分别选择一个样本,将其与测试样本一起,输入到SNN-LSTM网络中,得到测试样本属于每一类的概率值,选择概率最大那个类作为测试样本的类别。

2 实验数据及信号采集

2.1 实验数据

为了验证基于SNN-LSTM的故障诊断方法在轴承故障诊断中的有效性,笔者设计了一个轴承故障诊断实验,采集了不同转速、不同状态下的轴承振动数据[16]。

数据来源于Machinery Fault Simulator-Lite轴承故障诊断实验台。

实验台结构如图4所示。

图4 Machinery Fault Simulator-Lite轴承故障诊断实验台

笔者选用DEWE 43V采集卡采集传感器上的加速度信号。

其中,传感器品牌及型号为:KISTLER-8766A050。电动机转速分别为:1 200 r/min、1 800 r/min、2 400 r/min。轴承型号为:ER12K-HFF深沟球轴承。

采样频率为12 kHz,正常轴承采样时间为4 min,其他有故障的轴承采样时间为2 min。

传感器采集轴承基座上的振动信号,所采集到的故障类型是单一故障。其在1 200 r/min转速下,采集正常、滚动体故障、内圈故障和外圈故障4种状态的轴承振动信号;在1 800 r/min转速下,采集滚动体故障、内圈故障和外圈故障3种状态的轴承振动信号。

故障尺寸大小为1.5×0.8 mm,为电火花点蚀加工。

每种状态下所截取的信号长度为120 000个点,一半数据生成训练集,另一半生成测试集。每2 048个点为一个样本,在训练集上采用大小为2 048个点、滑动步长为80个点的滑动窗口生成训练样本,通过重叠采样的办法,可以扩充训练样本数量。

测试集上用同样大小的窗口生成测试样本,不采取重叠滑动。一共有7种不同状态类别,每个类别包括300个训练样本和100个测试样本。

数据集描述如表2所示。

表2 数据集描述

2.2 振动信号波形图

实验中,笔者采集到了在1 200 r/min转速下的4种状态的轴承振动信号时域波形图,如图5所示。

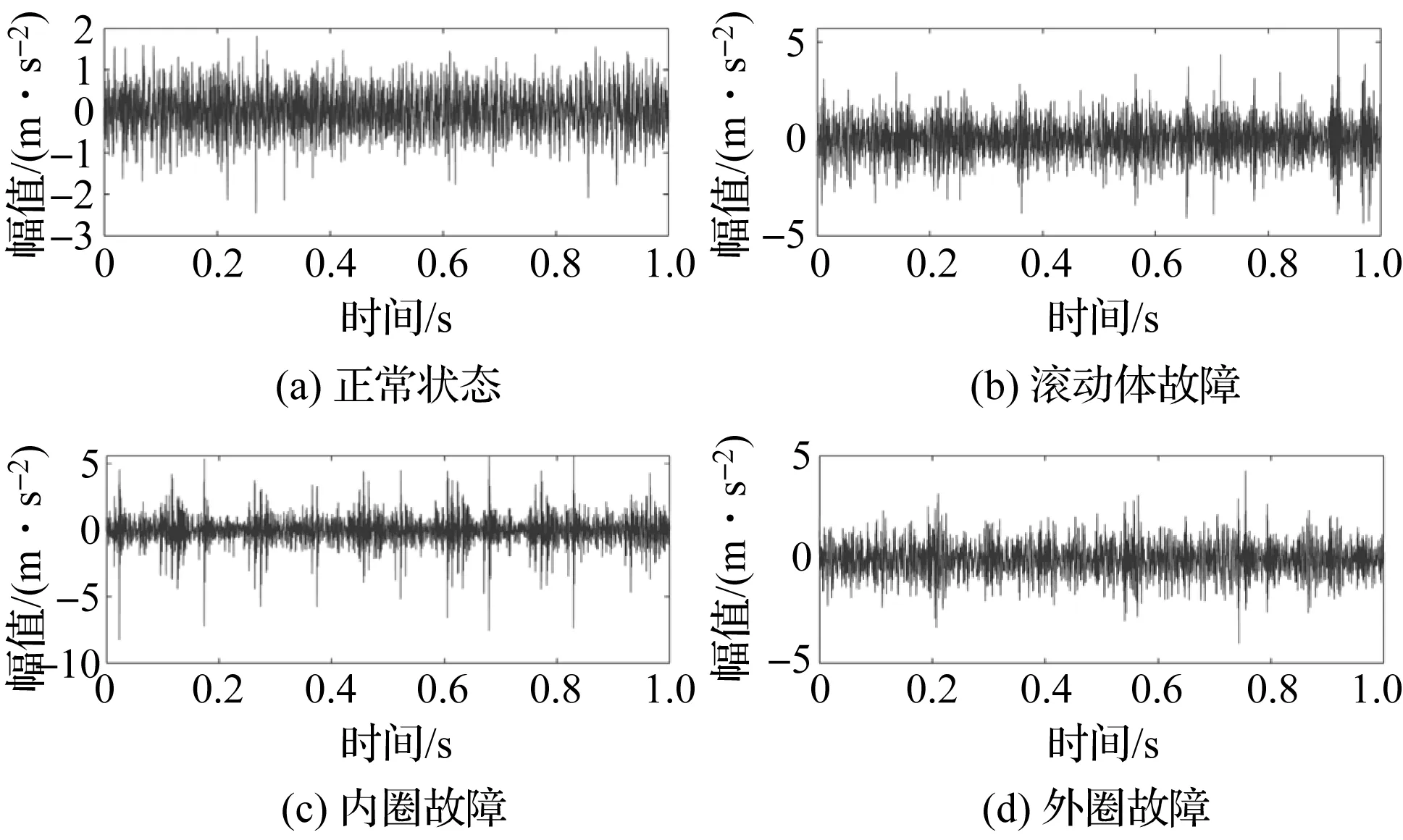
图5 在1 200 r/min转速下的轴承振动信号时域波形图

实验中,采集到在1 800 r/min转速下3种状态的轴承振动信号时域波形图,如图6所示。

图6 1 800 r/min转速下的轴承振动信号时域波形图

3 实验结果分析

3.1 不同训练样本数量下各个网络的准确率

笔者在训练集里选择35、70、140、210、350、420、700、1 400、2 100个训练样本,以及全部700个测试样本,并将其输入到网络中。

为了验证在小样本数据下,基于SNN-LSTM网络的方法的优越性,笔者建立与SNN-LSTM子网络结构一致的CNN-LSTM网络,与上述方法进行对比。同时,建立去掉长短时记忆网络层后的SNN网络,与上述方法进行对比;每次实验重复10次后,取平均值得到准确率。

实验结果如图7所示。

图7 在不同训练样本数量下各个网络的准确率

对比SNN-LSTM和SNN可以发现:

在不同训练样本数量下,SNN-LSTM的准确率都要高出SNN大概2%～4%,说明加入长短时记忆网络层,可以提高轴承故障分类的准确率;

对比SNN-LSTM和CNN-LSTM可以看出:

当训练样本数量超过700个时,两个网络的准确率相差只有不到1%,并且二者的准确率都超过95%。随着训练样本数量的增加,二者的准确率也随着增加;

当训练样本数量在35～140个时,SNN-LSTM的准确率要明显高于CNN-LSTM的准确率;

在训练样本数量仅为35个时,SNN-LSTM仍然有61.28%的准确率,而CNN-LSTM只有41.25%的准确率,高出20.03%。

该结果说明,SNN-LSTM在样本数量较多的时候网络的性能没有多少损失;同时,在小样本数据下比CNN-LSTM的准确率高得多。

以上结果证明,基于SNN-LSTM的方法比现有的神经网络方法更适合于小样本数据。

3.2 模型可视化

为了更直观地表示神经网络在故障诊断中的效果,笔者采用t-SNE降维的方法,对SNN-LSTM在140个训练样本情况下的全连接层进行降维可视化。

模型全连接层的t-SNE可视化如图8所示。

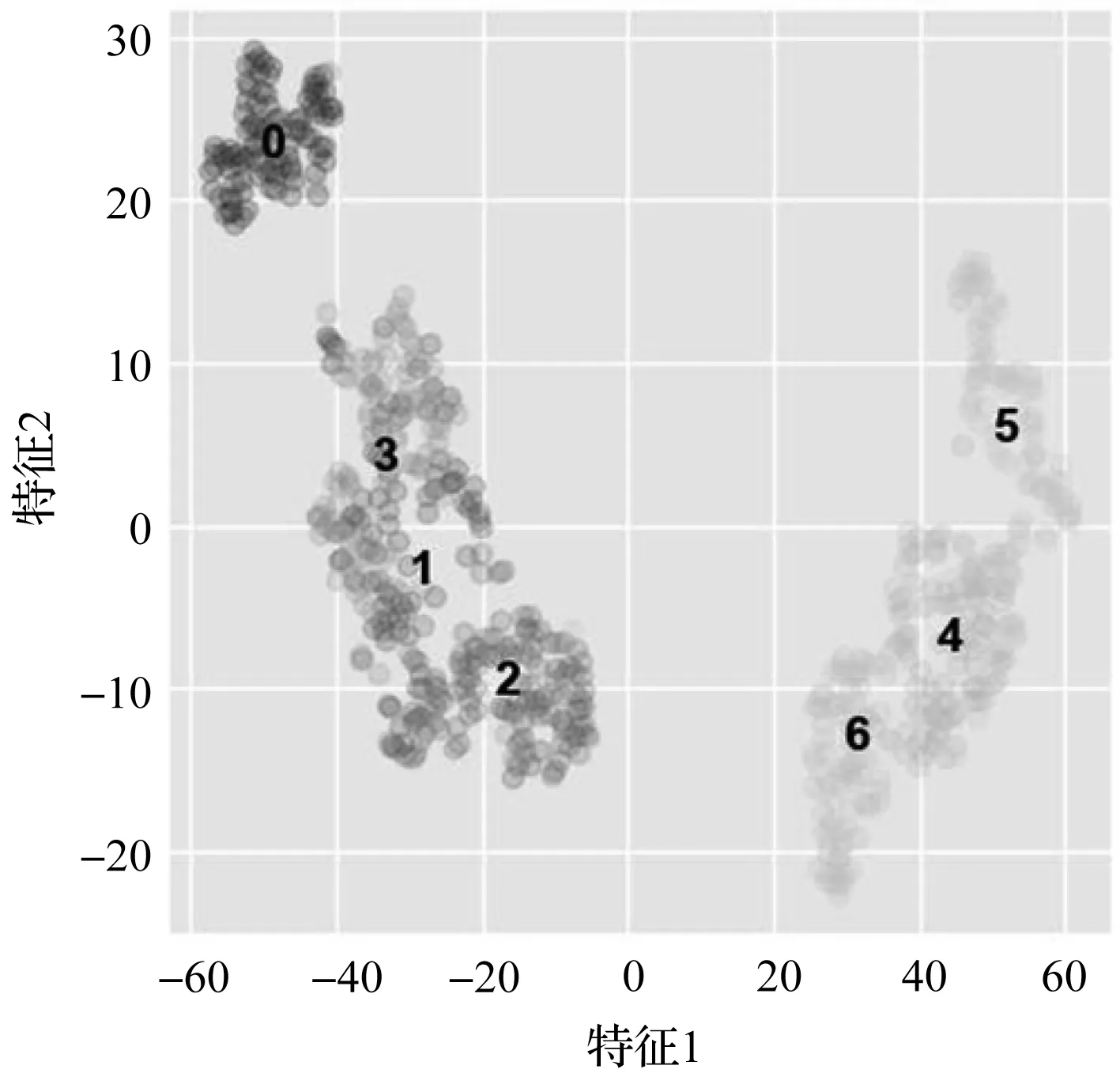
图8 模型全连接层的t-SNE可视化

同时,笔者给出在700个测试样本下的混淆矩阵,如图9所示。

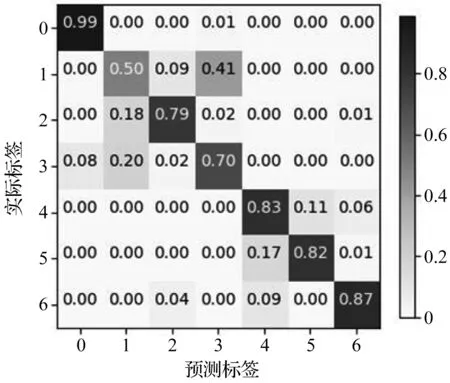
图9 测试结果混淆矩阵

从图(8,9)中可以看出:

SNN-LSTM故障诊断方法除了将1类中的接近一半测试样本误分成3类外,对于其余6个类的分类效果尚可:其中,对于0类的分类准确率最高接近100%;

对于3类的分类准确率较低为70%,其中,将20%的测试样本误分到1类里。

4 结束语

在小样本数据下的轴承故障诊断中,采用基于经典神经网络方法时,存在模型欠拟合和分类准确率低等问题,为此,笔者提出了一种基于SNN-LSTM的轴承故障诊断方法,并将其应用于小样本数据下的轴承故障诊断中。

研究结果表明:

(1)神经网络的输入是原始振动信号,从而减少了经过数据处理或者数据转化时产生的数据误差,同时避免了相对主观的人工提取方法;

(2)经过实验验证,在网络中加入长短时记忆网络层后,在不同训练样本数量的条件下,均可以提高网络的准确率,提高2%～5%;

(3)通过对比SNN-LSTM和CNN-LSTM在不同训练样本数量下的准确率,可以看到:当训练样本数量在700～2 100个之间时,二者的准确率均超过95%,并且相差不大;当训练样本数量在35～140个之间时,SNN-LSTM比CNN-LSTM的准确率高出20%左右;在训练样本数量仅为35个时,SNN-LSTM的准确率仍有61.28%,而CNN-LSTM的准确率只有41.25%。

在后续的研究过程中,笔者将加入三一集团有限公司不对中滚动轴承数据来进行故障的分类,研究实际工程数据对上述诊断模型的影响。