基于并行协同的多车间协同调度问题研究*
冯润晖,董绍华
(北京科技大学 机械工程学院,北京 100083)
0 引 言
在通常情况下,制造企业的生产过程可以分成加工和装配两个阶段,再由多个加工车间和装配车间组成一个多车间混合生产系统[1]。
在以往的研究中,将加工和装配两个阶段独立考虑,分别考虑每个车间的生产计划和调度。首先加工车间加工零部件,然后将半成品进行仓储,待所有配套零部件就绪后,再进行产成品的装配[2]。由于生产计划与调度的研究对象是单车间环境,只在车间内部实现了制造资源合理配置,无法兼顾制造系统整体效益,导致了产品生产周期增长和零部件库存费用增加等一系列问题,致使其生产效率较低。因此,对多个有关联的车间进行统一集成优化调度研究十分必要且意义重大,这是生产系统优化的关键问题。
在协同制造环境下,2个或2个以上具有独立生产能力的车间,组成了一个相互配合、目标一致的生产共同体,对其合理安排生产,在满足工艺约束的前提下,协同一致地达到目标函数最优化的过程,称为协同调度[3]。
现阶段,国内外学者们对协同调度问题的关注度较高。BHATNAGAR R等人[4]总结了协同调度问题的相关文献,为集成的多车间协同调度生产计划建立了数学模型,以最适合整个组织的方式,确定了所有工厂的生产决策。BEHNAMIAN J等人[5]将多车间协同调度的文献,根据车间环境进行了整理分类,并对综述文献进行了对比,以确定有效的调度可以提高生产率。NADERI B等人[6]研究了最小化完工时间的分布式流水车间调度问题,设计了分散搜索算法,并对其进行了求解,结果表明,该算法比现有算法具有更好的效果。XU Ye等人[7]研究了分布式置换流水车间的调度问题,设计了混合免疫算法,并对其进行了求解,证明了该算法的有效性。NA H等人[8]研究了加工与装配制造车间投产排序问题,并以总延迟时间最小为目标构建了模型,以便在设定的日期之前完成零件。秦金涛[9]采用了多代理和规则引擎技术,在制造执行系统中构建了调度协同平台,实现了不同车间生产制造信息共享的目标,提高了制造企业各车间协同生产的效率。董义军[10]建立了面向客户可承诺(available to promise,ATP)的多工厂生产计划调度数学混合规划模型,设计了基于遗传算法的多工厂协同生产计划模型的求解算法。孙亚南等人[11]借鉴了面向对象的设计思想,以及基于模糊数学的最大隶属度原则,提出了面向产能瓶颈单元的协同调度问题方法,解决了如何在有限资源的情况下,实现复杂制造系统最优化调度的问题。于晓义等人[12]为求解多协作车间的计划调度问题,提出了并行协同进化遗传算法,以满足多协作车间并行协同调度的要求。梁迪等人[13]提出了一种协同奔袭策略的狼群优化算法,将改进后的狼群优化算法应用在双车间协同调度问题上,并对此进行了验证,证明了该算法具有明显的优势。王艳等人[14]建立了以制造总成本与提前/延期为优化目标的分布式多工厂调度模型,提出了一种融合决策树的高斯粒子群嵌套寻优算法框架,验证了该算法在寻优性、收敛性和CPU时间方面的优越性。李修琳等人[15]运用了集成模拟退火算法的混合遗传算法,求解了具有多品种混流生产特征和作业车间,及流水车间集成的混流混合车间协同调度问题。廖不凡等人[16]提出了一种混合教学优化算法,以完工时间为目标,解决了多车间协作综合调度问题,提高了各车间设备资源的利用率,并缩短了产品加工的总时间。
综上所述,已有的对多车间协同调度的研究文献中,场景大多限定在流水车间,以混合流水车间为原型进行研究的甚少。
混合流水车间一般定义为:流水线上有N个工件依次经过M个阶段的加工,其中每个阶段至少存在一台机器,并且至少有一个阶段存在多台机器可以进行加工。对同一工件的某个阶段,工件可以选取任意一台并行机来完成相应工序,不同并行机处理时间可能存在差异。混合流水车间调度问题(hybrid flow shop scheduling problem,HFSP)是一般流水车间调度问题的扩展,不仅涉及到工件的排序,也涉及到并行机的分配,且该问题已经被证明是典型的NP难组合优化问题(non-deterministic polynomial problems,NP)。
因此,笔者对多混合流水车间的协同调度问题进行研究,以完成所有订单加工和装配的总时间为优化目标,运用协同进化思想,采用并行协同进化遗传算法对其进行求解,并以某液压缸生产企业作为实验对象,验证所建模型和采用算法的实用性与有效性。
1 多车间协同调度问题建模
1.1 模型描述及假设
笔者研究的问题是以零件加工车间及产品装配车间组成的两阶段生产系统为基础,根据生产数据,建立模型。
s个相互协作的加工车间以及一个装配车间共同完成n种订单产品的生产装配任务:
加工车间集S={1…j…s};每个车间的生产阶段集P={1…k…p};订单产品集O={O1…Oi…On},每个产品由w个工件装配而成,每种产品Oi的数量xi;每种产品包含的工件W={1…a…w};因此Oiajk,x代表第x个产品Oi的工件a在车间j加工工序k。
各车间加工的工件各不相同,车间j有Mj台设备完成工件加工任务,不同加工阶段之间运送设备Vj完成工件运送任务:
加工设备集为Mj={1…m…Mjall};运送设备集为Vj={1…v…Vjall},Mjk为车间j阶段k的可选加工机器集。
为方便确定装配关系,设置加工和搬运批量均为1,不同批次工件的工序之间没有先后约束。必须在其子项工件加工完成后,装配任务才可以开始进行,每道工序必须在其之前所有工序加工完成后才可开始,每台加工设备同一时间只可同时加工一个工件。各工件的工序间是相互独立的生产任务单元。
1.2 模型建立
相关参数设计如表1所示。

表1 模型参数
笔者研究的问题以最小化订单完工时间为目标的单目标优化问题,因此,其目标函数如下:
minf=max{FAikm,x}
(1)
式中:f—目标函数。
式(1)中,目标为最小化订单完工时间,订单完工时间即为装配结束时间。
约束函数如下:
(1)加工车间约束
任一工件只能在一个车间内进行加工,工序之间不可跨车间加工;
(2)
(2)工件加工时间约束
各工件在各工序的完工时间,为该工序开始加工时间与该工序被加工时间之和;
Fiajkm,x=Siajkm,x+Piajkm,xwhenXiajkm,x=1∀i,j,a,k,x∈xi,m∈Mjk
(3)
各工序的开始加工时间,为其运输到该阶段的运输完成时间与该阶段加工机器所加工的前一工件的完工时间的较大值;
Siaj(k+1)m,x=max{Fi1aj(k+1)m,x1,FTiajk(k+1),x,v}
whenXiaj(k+1)m,x,Xi1aj(k+1)m,x1,Tiajk(k+1),x,v=1∀i,i1,j,a,k,x∈xi,x1∈xi1,m∈Mj(k+1),v∈V
(4)
(3)工序加工顺序约束
任一工件若想进入下阶段进行加工,必须完成上阶段的全部加工任务;
FTiajk(k+1),x,v+Piaj(k+1)m,x≤Fiaj(k+1)m,x
whenXiaj(k+1)m,x,Tiajk(k+1),x,v=1
∀i,j,a,k,x∈xi,m∈Mj(k+1),v∈V
(5)
(4)搬运设备运送时间约束
开始搬运时间为上一个工件的结束搬运时间与两机器间的运输时间之和;
STiajk(k+1),x,v=FTi2ajk(k+1),x2,v+MTm1,m2
whenXiajkm2,x,Xiaj(k+1)m1,x,Xi2aj(k+1)m1,x2=1,
Tiajk(k+1),x,v,Ti2ajk(k+1),,x2,v=1
∀i,i2,j,a,k,x∈xi,x2∈xi2
m1∈Mj(k+1),m2∈Mjk,v∈V
(6)
搬运结束时间为工件的开始搬运时间与两机器间的运输时间之和;
FTiajk(k+1),x,v=STiajk(k+1),x,v+MTm1,m2
whenXiajkm2,x,Xiaj(k+1)m1,x,Tiajk(k+1),x,v=1
∀i,j,a,k,x∈xi,m1∈Mj(k+1),m2∈Mjk,v∈V
(7)
(5)机器加工能力约束
在同一时刻,一个工件只能由一台加工机器进行加工;
t∈[Siajkm,x,Fiajkm,x],m∈Mjk,∀k,j,a
(8)
同一时刻,一台机器只能加工一个工件;
t∈[Siajkm,x,Fiajkm,x],x∈{1,2,…,xi},∀i,k,j,a
(9)
(6)运输能力约束
同批工件同一时刻只能由一台运输工具进行运输;
t∈[STiajkm,x,v,FTiajkm,x,v],∀i,k,j,a,v,x∈xi
(10)
同一台运输工具同一时刻只能运输同一批工件;
t∈[STiajkm,x,v,FTiajkm,x,v],∀i,k,j,a,x∈xi
(11)
(7)加工时间约束
所有阶段的加工时间为正数:
Piajkm,x≥0,x∈{1,2,…,xi},m∈Mjk,∀i,k,j,a
(12)
所有工序在0时刻均可被加工,即:
Siajkm,x≥0,x∈{1,2,…,xi},m∈Mjk,∀i,k,j,a
(13)
2 多车间协同调度问题求解
2.1 算法流程
针对上述调度模型,笔者提出了一种多车间协同调度的并行协同进化遗传算法(PCE-GA),并采用该算法对上述模型进行求解。
其算法流程如图1所示。
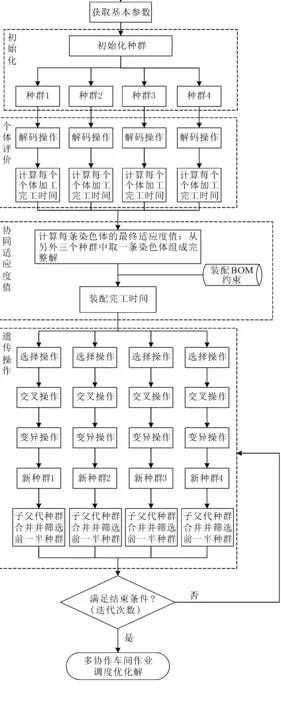
图1 并行协同进化遗传算法流程图
图1中的算法流程表明,种群与种群之间存在协作关系,所有种群合并形成一个完整解,种群内有竞争,种群间有协作,各个种群的进化过程并不是相互独立的,而是协同进化,更加符合自然界进化的规律。
2.2 并行协同进化遗传算法
2.2.1 染色体编码
为了同时描述工件的加工顺序、加工机器和装配关系3种信息,个体的染色体编码采用三层整数编码方式,每一个三层编码对应一个调度方案,种群初始化采用按工序随机生成原则,终止准则为预先设定的最大迭代次数。
编码第一层为基于工件的编码,工件号出现的次数代表该工件的工序数;第二层为基于机器的编码,代表该工序选择的加工机器的编号;第三层为基于装配的匹配关系的编码,不同种群中装配码相同代表具有装配关系。
染色体的编码方式如图2所示。
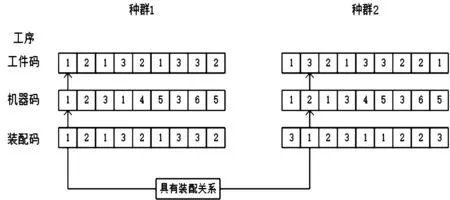
图2 编码方式
由图2可知:种群1中某条染色体编码为[1,2,1,3,2,1,3,3,2,1,2,3,1,4,5,3,6,5,1,2,1,3,2,1,3,3,2];其中,前三分之一[1,2,1,3,2,1,3,3,2]为工件码,代表工序{O11,O21,O12,O31,O22,O13,O32,O33,O23};其中,Oij代表第i个工件的第j道工序,机器码为中间三分之一部分[1,2,3,1,4,5,3,6,5],代表工件某工序选择的机器号,即工序O11选择机器1,工序O21选择机器2,装配码为最后三分之一部分,如图2箭头所示,种群1的工件1与种群2的工件3具有相同装配码,因此,具有装配关系,同理种群1的工件2和种群2的工件2、种群1的工件3和种群2的工件1具有装配关系。
2.2.2 协同适应度值计算
采用PCE-GA算法计算个体适应度值时,需要计算两次适应度值。
协同适应度值计算流程如图3所示。
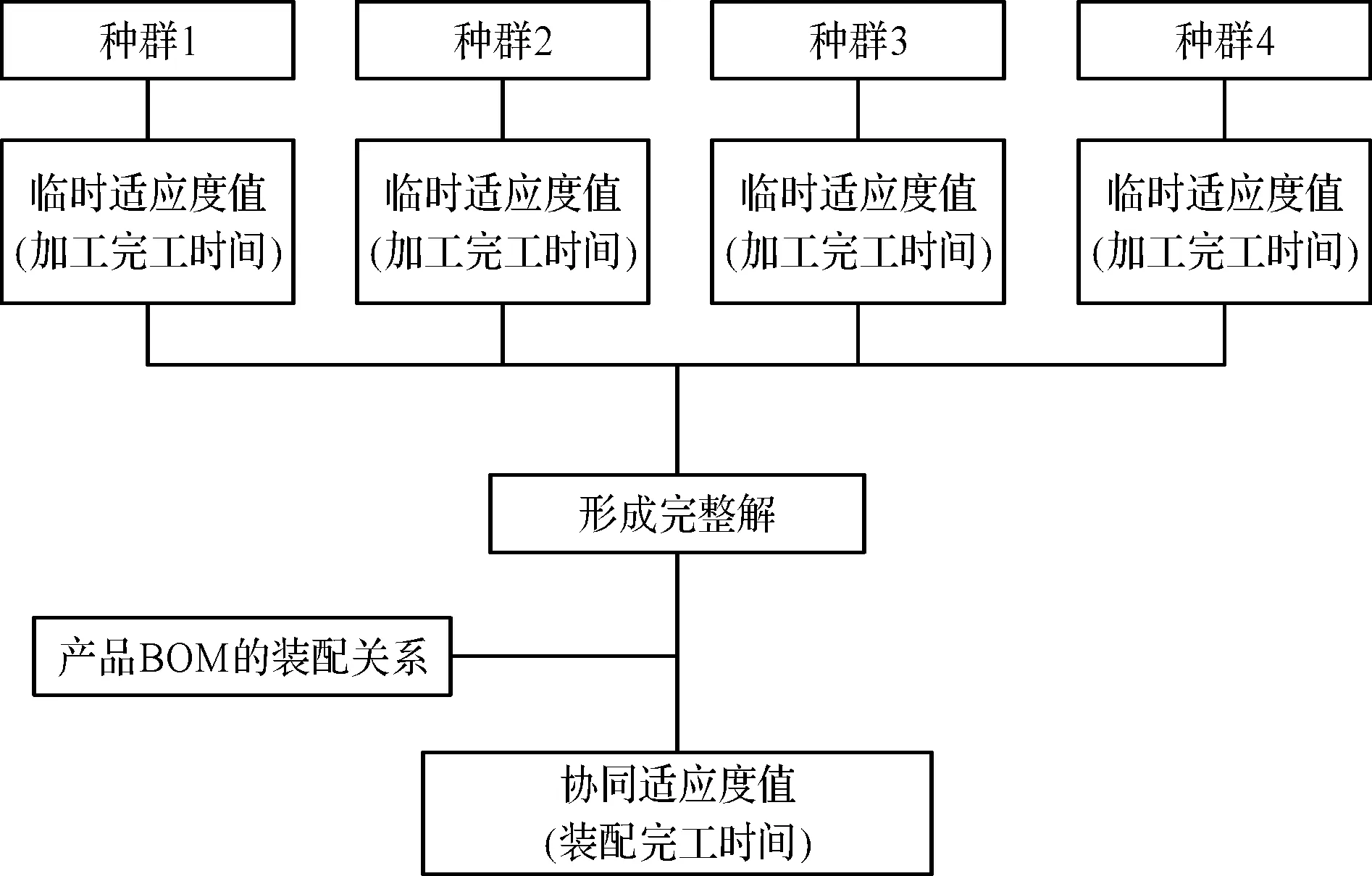
图3 协同适应度值计算流程
首先,笔者分别单独计算每个种群中每条染色体的适应度值,即每条染色体对应的调度方案的加工完工时间,作为该个体的临时适应度值;然后计算协同适应度值,方法为对于任一种群中的每一条染色体,与其他每个种群中的一条染色体合并作为一个完整解,根据物料清单(bill of material,BOM)表中的零件装配关系,计算该完整解的装配完工时间,作为该条染色体的协同适应度值。
2.2.3 选择交叉变异操作
为了将最优个体保留,笔者采用精英保留策略,将每一代中最好的个体保留至下一代,不进行交叉变异操作。选择操作采用锦标赛选择策略,每次从种群中取2个个体(放回抽样),选择其中完工时间较小的个体进入子代种群。重复该操作直到种群规模和原来的种群规模一样。
交叉操作采用工件层的单点交叉法,父代在工件码中随机选择交叉点,在交叉点前的基因互换,之后比较父子代染色体,将子代中多余的工件号替换成缺失的工件号,以此保证子代染色体为可行的调度方案,保证子代每道工序所分配的机器与父代一致,最后装配码则根据交叉完的工件码重新生成。
个体交叉示意图如图4所示。
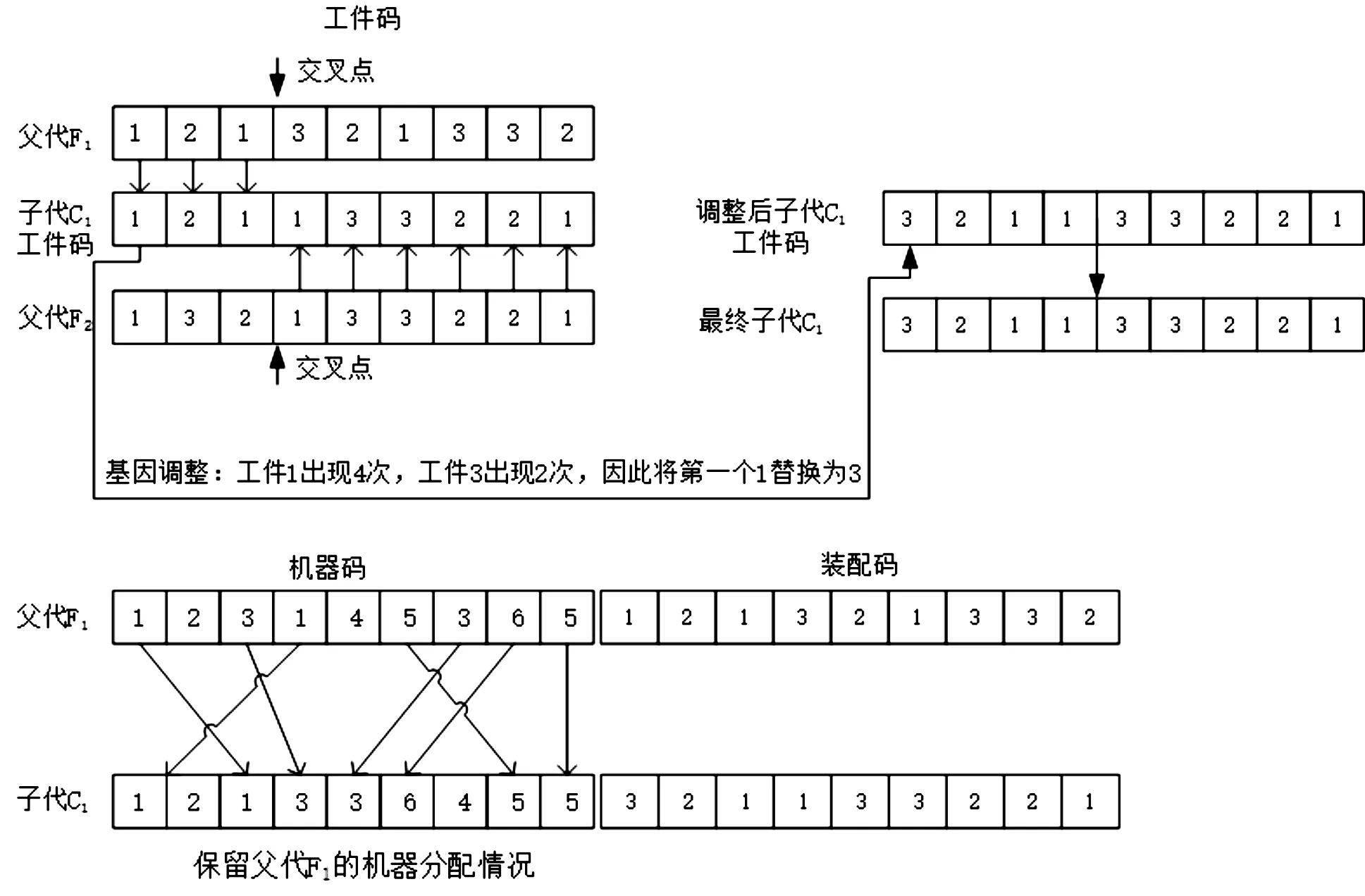
图4 个体交叉示意图
图4中,父代交叉点为第4个基因,交叉完成后子代保留父代的机器基因。
变异操作主要针对机器码,随机选取多个变异点,将机器变为该工序机器可选集中的其他机器。
3 实验及结果分析
为了验证PCE-GA算法的优越性,笔者以某液压缸制造企业为实验对象,对多车间协同调度算法进行研究。液压缸的加工零部件包含外罩、外缸、缸筒和末级。
各个车间之间的协作关系如图5所示。
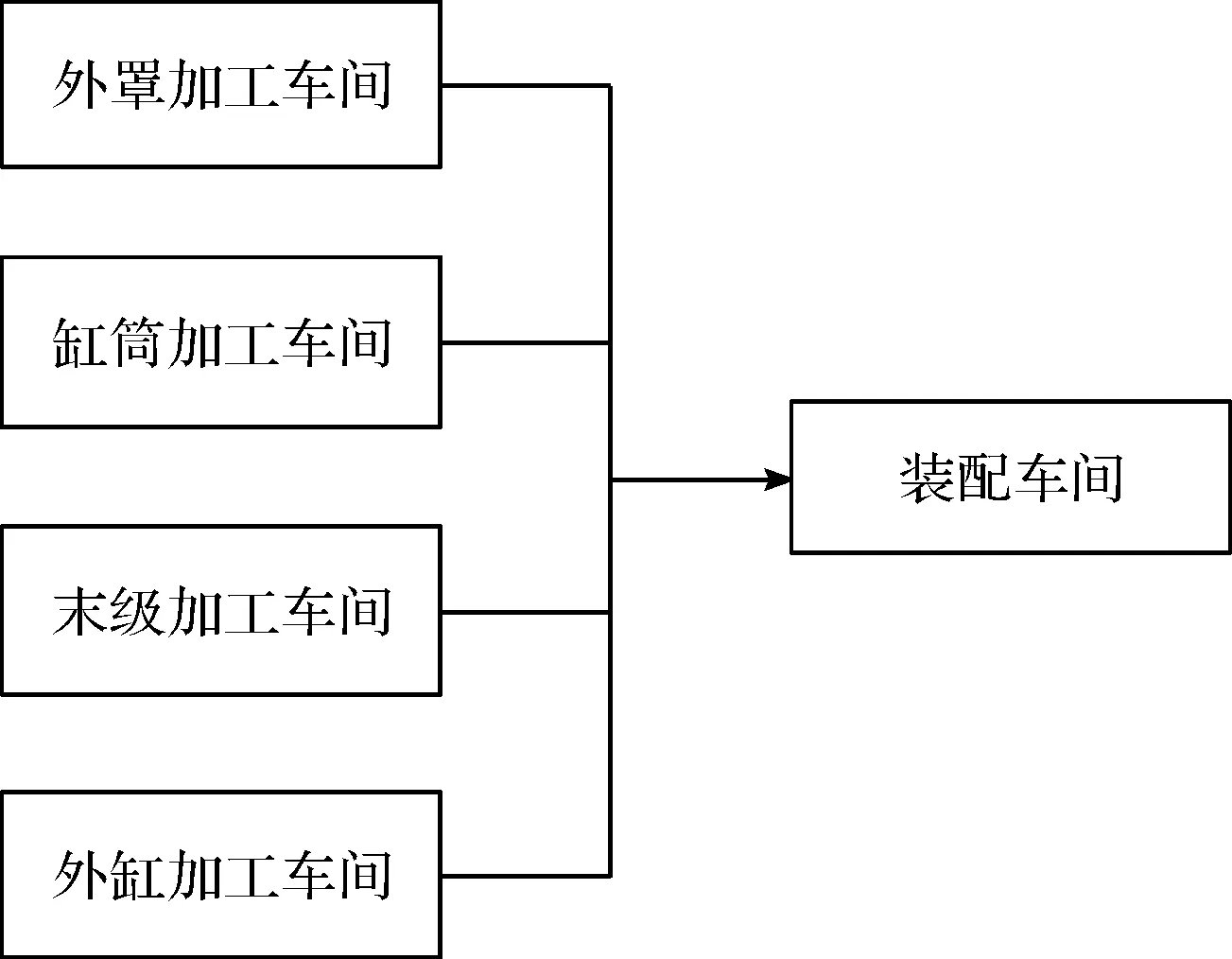
图5 液压缸生产车间协作关系
图5中,液压缸的各个零部件在不同的车间分别进行加工,加工完成后的各个零部件和外购的零件集中在一起进行装配,得到液压缸产品。该企业的每个生产车间可被抽象为混合流水车间。
外缸加工车间的设备如表2所示。
不同车间的加工机器不同,根据表2可知:该车间共有26台加工设备,8个加工阶段,每个阶段都包含并行机。
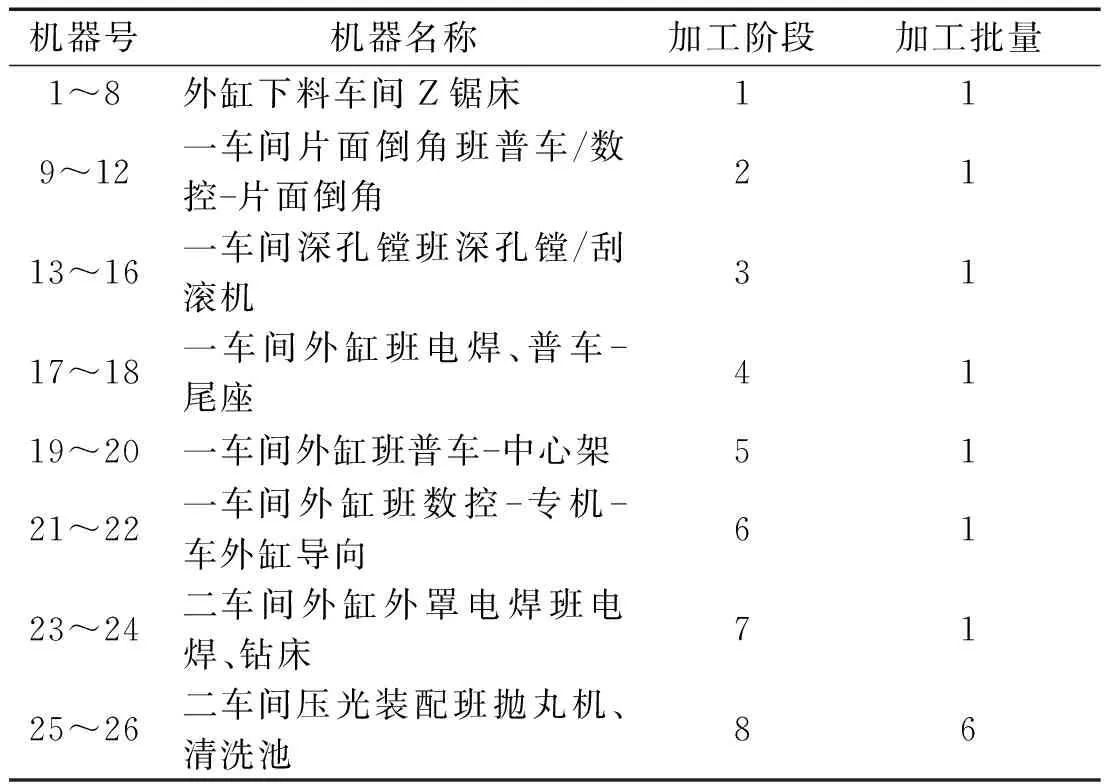
表2 外缸加工车间设备表
现对4个订单19件产品进行排产,产品信息及装配关系如图6所示。
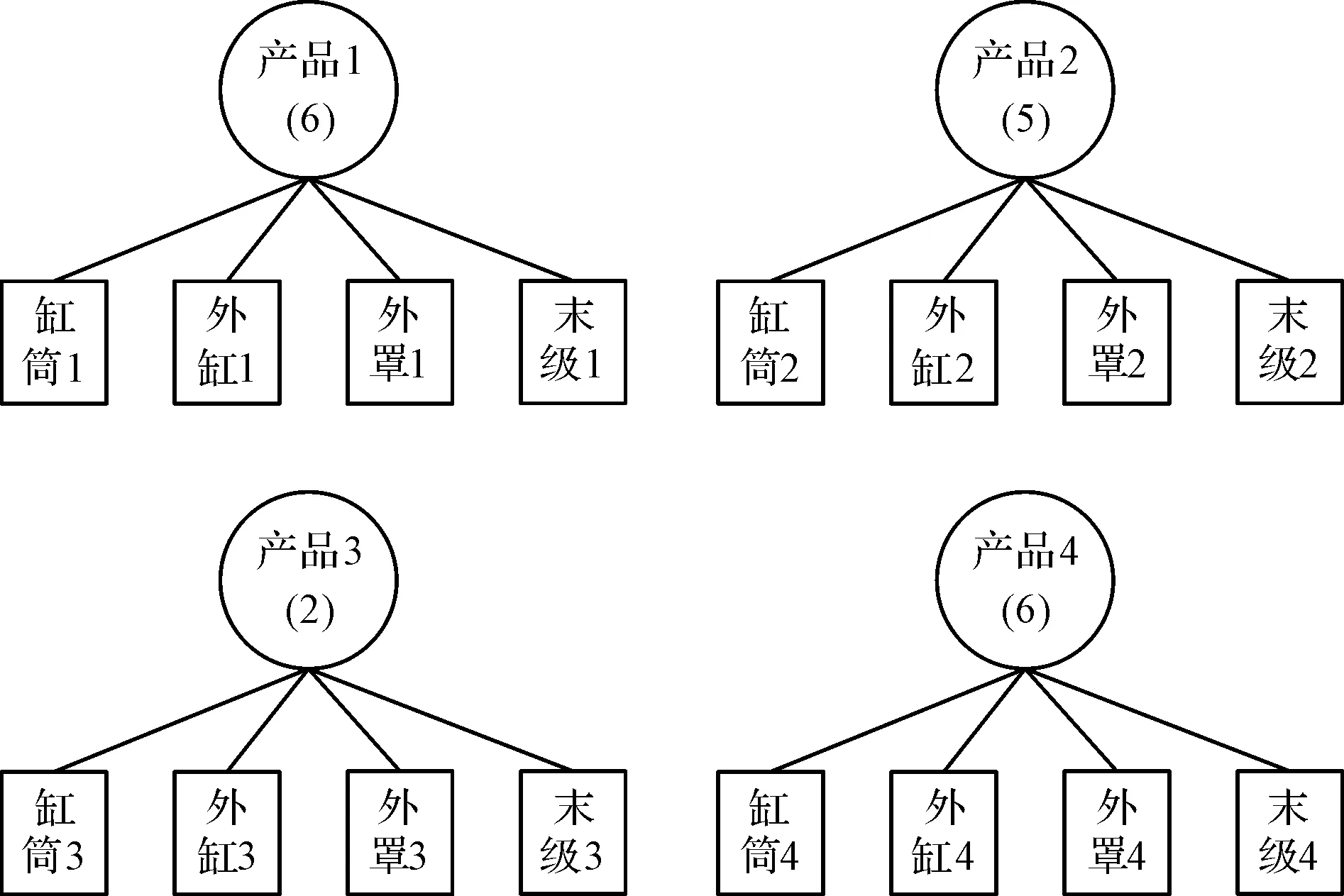
图6 产品信息及装配关系圆圈代表装配件,方框代表加工零部件,括号内是订单数量。
因为模型假设中定义的加工批量为1,因此,每个产品都有不同的装配码,对19个产品编号为1~19,每个零件与所属产品具有相同的装配码编号。不同订单的相同零件因具有不同的装配码编号,因此,是分开依次进行排产的,且不同订单的优先级相同,所有订单按BOM表分解后有76个零件加工生产任务,19个组合件装配生产任务。
为了验证上述模型与求解方法的实用性和有效性,笔者设置2组实验。
其中,遗传算法的参数为:种群数量为500,交叉概率为0.8,变异概率为0.1,迭代次数为20。用QT 4.11.1进行编程,算法运行环境为Intel(R) Core(TM) i7-8565U CPU @ 1.80 GHz 1.99 GHz,16.0 GB运行内存,Window10 64位操作系统。
3.1 实验一
接下来,笔者进行并行协同进化遗传算法(PCE-GA)的求解。
通过运用上述PCE-GA算法,在调度起始时间t=0、设备初始能力充足的情况下,对该企业的上述实际订单进行运算。
进化过程中每一代的最优解如图7所示。
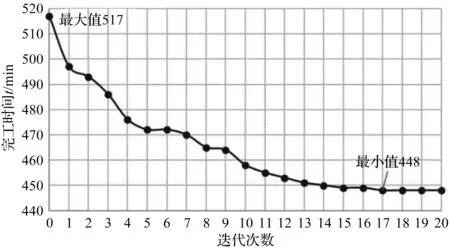
图7 协同进化收敛曲线
由图7可知:在20次迭代过程中,最优解的值不断下降,在第17代趋于平稳地收敛到最终的优化解。其中,最大值为517 min,最小值为448 min,优化率13.3%。
最优解调度方案对应的订单中,产品的各个部件完工时刻以及装配完工时刻,如表3所示。

表3 完工时刻表
由表3可以看出:外缸为瓶颈部件,因为0时刻为该组订单的开始加工时刻,因此,该组订单的最终完工时间为448-0=448 min。
3.2 实验二
接下来,笔者进行3种算法求解效果的对比。
为了进一步体现算法的优势,笔者将PCE-GA算法与单车间作业调度遗传算法(JSP-GA)及并行协同进化模拟退火算法(PCE-SA)进行比较。
单车间作业调度即分别对每个车间单独进行优化,将最晚完工的车间结束时间作为装配的起始时间,对装配车间进行优化,得到最终的完整解,即订单完工时间。
PCE-SA算法也采用并行协同进化思想进行求解(模拟退火算法的参数设置为:初始温度为500,停止迭代温度为0.1,降温速度为0.75,在每个温度下设置内部蒙特卡洛循环迭代次数为10)。
3种算法求解结果如表4所示。
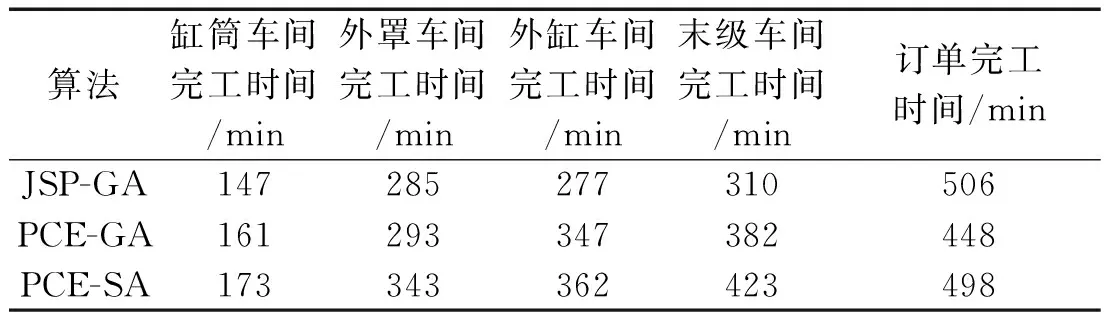
表4 3种算法的求解结果
由表4可知:对于单个车间,JSP-GA算法求解的每个车间的调度方案完工时间,都比PCE-GA算法和PCE-SA算法求解的完工时间要短,但应用并行协同进化算法求解的订单完工时间却要比单车间调度算法求解的订单完工时间短,即在整体层面上,PCE-GA算法产生的调度方案,其构成完整解的质量比单车间遗传算法产生的解优越,优化率为11.5%。
单车间遗传算法仅实现了车间局部的优化,未能实现企业整体最优。虽然PCE-SA算法的订单完工时间比PCE-GA算法的结果要长,但仍比JSP-GA算法求解结果略好,再次证明了PCE-GA算法的优越性。
4 结束语
传统企业在实际生产中,其多个关联车间之间的生产计划与调度存在难以协作的问题。为此,针对该多混合流水车间的协同调度问题,笔者以完成所有订单加工和装配的总时间为优化目标,运用协同进化思想,采用并行协同进化遗传算法对其进行了求解,并以某液压缸生产企业作为实验对象,验证所建模型和采用算法的实用性与有效性。
研究结论如下:
(1)在实验一中,采用PCE-GA算法求解得到的优化率为13.3%,说明该算法在解决该类复杂组合优化问题时是有效的;
(2)采用PCE-GA算法比JSP-GA算法求解的数据优化了11.5%,该结果表明,运用协同进化思想能够有效地协调各协作车间的生产活动,可以明显提高企业的整体生产效率。
在目前的研究中,笔者所采用的优化目标为订单完工时间。在后续的研究过程中,笔者将会增加研究目标,例如搬运时间等,并且在此基础上,针对不同订单交货期设置优先级。

