基于RCMRFDE和ELM的滚动轴承故障检测方法*

周经龙,乔惠萍

(1.北京大学 智能学院,北京 100091;2.重庆科创职业学院 人工智能学院,重庆 402160;3.山西工程科技职业大学 计算机工程学院,山西 晋中 030031)

0 引 言

滚动轴承易发生疲劳失效而导致结构故障。如何有效地检测滚动轴承的故障是轴承健康监测领域研究的重点[1]。

当轴承发生故障时,其振动信号表现出非线性和非平稳的特征[2]。采用线性分析的方法对该类信号特性进行描述时,常常存在不足之处。采用非线性的方法中,常用的非线性方法如熵,由于它能够快速地度量复杂序列的不规则度,在各领域得到了广泛应用[3]。

例如,杨云等人[4]采用排列熵(permutation entropy,PE),提取出了振动信号(经变分模式分解处理后)的模态分量中的故障信息,使得滚动轴承故障诊断的准确率达到了93.75%,该诊断结果表明,PE能够有效地量化轴承的故障特征。

然而,PE是基于数据振幅出现的顺序来进行熵的估计,因此,它忽略了数据的振幅信息。

为了解决PE的缺陷问题,吴新忠等人[5]采用了加权排列熵(weighted permutation entropy,WPE)来代替排列熵,用以提取出滚动轴承的故障特征,并将其与能量熵和PE进行了分类结果对比,结果表明,WPE的性能优于能量熵和PE,基于WPE的故障诊断方法的识别准确率更高。葛红平等人[6]提出了一种粒化幅值感知排列熵(amplitude aware permutation entropy,AAPE),将其用于滚动轴承的故障诊断,并将其所得结果与采用排列熵所得结果,在准确率和聚类效果方面进行了对比,结果表明,AAPE在准确率和特征聚类效果方面均优于PE。

在计算排序模式出现的概率时,WPE和AAPE通过引入振幅信息,以此来对PE进行改进。当数据振幅差异较小,而系统本身具有较大的复杂度时,采用WPE和AAPE的方法将不再有效[7]。

同样,为避免PE的缺陷,ROSTAGHI M等人[8]开发了散布熵(dispersion entropy,DE);并利用多种信号对DE和PE的性能进行了比较,结果表明,在数据不规则度的量化方面,DE比PE更加准确。夏理健等人[9]提出了一种基于散布熵的滚动轴承故障诊断方法,研究结果证明,DE具有较好的性能。吴守军等人[10]提出了一种基于变分模态分解的散布熵特征提取方法,结果证明,在特征提取效率和识别准确率方面,采用散布熵要优于采用样本熵和排列熵方法。

然而,原始DE算法的特征提取性能依然存在优化改进的空间。因此,在DE的基础上,出现了各种改进算法。例如,AZAMI H等人[11]提出了波动散布熵(fluctuation dispersion entropy,FDE), LI Yu-xing等人[12,13]提出了反向散布熵(reverse dispersion entropy,RDE)和两者的组合方法,即反向波动散布熵(reverse fluctuation dispersion entropy,RFDE)。

与DE相比,RFDE考虑了数据中邻近元素的区别,对数据的部分或整体趋势去趋势化后,再引入了距离信息,能够准确地估计出信号的复杂度。

然而,RFDE只是从单一的尺度来描述信号的波动,对信号的分析仍然不够全面。对于振动信号而言,故障信息分散在多个尺度上,仅靠单一尺度的故障特征无法挖掘信号中深层次的信息[14]。

为此,LI Yu-xing等人[15]在RFDE的基础上,引入了精细复合粗粒化处理方式,实现了信号的多尺度分析,提出了精细复合多尺度反向波动散布熵(RCMRFDE)方法,并将其用于舰船辐射噪声的分析。最后,通过与其他几种多尺度方法进行对比,验证了RCMRFDE在增强特征区分度和稳定性方面优于其他方法。

目前,基于滚动轴承的故障诊断方法大多是将正常轴承和故障轴承同时进行故障特征提取和模式识别。然而,由于特征提取中的波动和模式识别中的不确定性,可能会将正常轴承归为故障轴承,从而给出错误的维修方案。为了避免该情况的出现,要禁止健康轴承进入到模式识别的步骤中。

为了有效地提升滚动轴承故障诊断的可靠性和准确性,鉴于RCMRFDE方法在描述非线性序列复杂度和特征提取方面的优势,笔者将其引入到故障诊断领域,并用于提取滚动轴承的多尺度故障特征,提出一种结合RCMRFDE和极限学习机(ELM)的滚动轴承故障检测方法。

笔者利用滚动轴承故障数据,将该故障检测方法分别与基于多尺度散布熵(multiscale dispersion entropy,MDE)、多尺度波动散布熵(multiscale fluctuation dispersion entropy,MFDE)和多尺度反向波动散布熵(multiscale reverse fluctuation dispersion entropy,MRFDE)方法进行对比。

1 精细复合多尺度反向波动散布熵

1.1 反向波动散布熵

FDE考虑了信号的波动能够有效的识别随机性的序列,而RDE噪声鲁棒性强,RFDE结合了两种方法的优势。RFDE的原理为:

(1)

式中:μ—期望;σ—标准差。

(2)利用线性变换,将y映射至[1,2,…,c],即:

(2)

式中:round—四舍五入函数;c—类别。

随后,x中的元素均被映射至[1,2,…,c]内。

(3)

式中:m—嵌入维数;λ—延迟。

(4)

(5)每个散布模式的概率为:

(5)

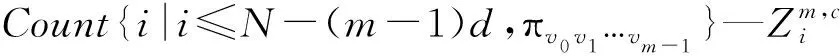
(6)结合距离信息,并基于原始信号与白噪声的距离,RFDE计算为:

(6)

1.2 精细复合多尺度反向波动散布熵

对于时间序列X={x1,x2,…,xN},基于下列步骤来计算其MRFDE和RCMRFDE[16]。

(7)

式中:τ—尺度因子。

计算各粗粒度序列的RFDE,即得到时间序列X的MRFDE。

(2)MRFDE的粗粒化处理存在缺陷,会遗漏大量有效信息。例如,当尺度因子为2时,根据式(7)的粗粒化处理,会遗漏x2和x3之间的信息,无法最大化数据信息。因此,采用复合粗粒化处理代替传统的粗粒化处理来实现RFDE的多尺度分析,称为RCMFDE。

RCMRFDE的原理如下:

对于时间序列,第n个粗粒度时间序列由下式进行计算:

(8)

RCMRFDE计算如下:

(9)

复合粗粒化综合考虑了序列中数据的内在关系,避免了传统粗粒化的信息遗漏问题。

2种粗粒化方法在尺度因子为2时的多尺度过程,如图1所示。

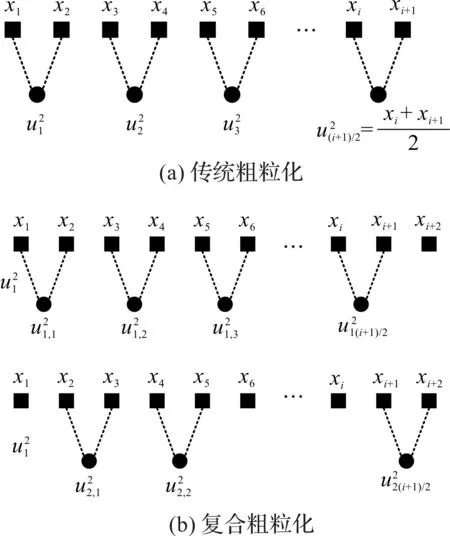
图1 τ=2时2种粗粒化过程

从图1可以发现:复合粗粒化处理对于时间序列的利用效率更高,数据之间的互相关性都得到了充分地考虑,优于传统的粗粒化处理。

1.3 参数选择

RCMRFDE需设置嵌入维数m、类别c、延迟d。对于m而言,太小,会无法检测到数据的动态变化;过大,无法捕捉到数据的微小波动,遗漏关键信息。文献[17]推荐m=2。

对于c而言,过小,造成可供分配的类别数目过少,使具有较大振幅差异的元素被归为同一类别,丢失振幅信息;反之过大,会增加可分配的类别数,使本该处于相同类别(具有较小振幅差异)的元素被划分为不同类别,影响算法抗噪性。基于以上原因,笔者设置c=5。

延迟对算法的性能基本没有影响。尺度因子的选择基于大多数文献的建议,即τ=20。

2 仿真信号分析

为了验证RCMRFDE的性能对数据长度不敏感,笔者生成了不同长度的WGN和1/f噪声,依次为1 000,1 500,2 000,2 500,3 000,3 500,4 000。

计算2种随机信号的MRFDE和RCMRFDE,结果如图2所示。

图2 不同长度WGN和1/f噪声的MRFDE和RCMRFDE

由图2可以发现:随着尺度的增加,2种噪声的MRFDE曲线波动得更加剧烈,特别是长度为1 000时,MRFDE波动的幅度非常大;相反,RCMRFDE曲线表现出良好的平稳性,随着尺度的增加,曲线的波动也明显小于MRFDE;

此外,在处理长度为1 000的序列时,RCMRFDE仍然取得了非常稳定的结果,这表明,在分析短时间序列时,RCMRFDE更具有稳定性;

因此,在后续分析中,长度设置为2 000。

随后,笔者进一步来验证RCMRFDE相较于MRFDE的优势。此处生成了40组长度分别为1 000,1 500,2 000的WGN和1/f噪声。

笔者分别采用RCMRFDE和MRFDE分析以上3种长度信号,并计算其得到的标准差差值。

熵值标准差差值结果如图3所示。

图3 3种长度随机信号的2种熵方法的标准差

从图3可以发现:对于3种长度的随机信号,在大多数尺度上,RCMRFDE的标准差均明显小于MRFDE;特别是在尺度因子较大时,2种熵方法的标准差差值明显较大,这证明了RCMRFDE方法适合用于分析短时间序列。

3 基于RCMRFDE和ELM的故障检测方法

基于以上的分析,笔者提出了一种用于实现滚动轴承综合故障检测的分级方法。该方法第一步是利用RCMRFDE对滚动轴承的故障状态进行预估,通过确定检测阈值筛选出来健康轴承;随后,利用RCMRFDE和ELM的混合模型来实现剩余滚动轴承的故障识别。

该综合故障检测方法的步骤如下:

(1)采集滚动轴承振动信号。设有h个工况。每个工况的数据分割成长度为2 000的互不重叠样本,设每个工况有N个样本,随机选取M个样本作为训练样本,剩余N-M个为测试样本;

(2)在尺度因子为20时,计算全部健康样本的RCMRFDE值,设[E1,…,Ei,…Em]为全部健康样本的第20个尺度的熵值,则健康检测时的阈值为：

(10)

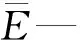
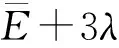
RCMRFDE之所以能够用于检测滚动轴承是否存在故障,是因为健康轴承振动信号较复杂,而故障振动信号中存在周期性的脉冲,复杂度较低。因此,故障轴承信号和健康轴承信号的熵值存在差异,导致健康轴承的RCMRFDE值小于故障轴承,从而能够完成样本的检测;

(3)经过健康检测后,若证明样本存在故障,则利用RCMRFDE方法提取20个尺度的熵值。在提取完全部故障样本的特征后,可获得故障特征库;

(4)将训练样本的故障特征输入至ELM分类器进行训练,生成完备的分类器。随后,将测试样本输入至分类器进行故障识别。

4 实验验证

4.1 实验一

4.1.1 实验及分析

为了验证基于RCMRFDE和ELM的故障检测的有效性,笔者利用美国凯斯西储大学(Case Western Reserve University,CWRU)提供的滚动轴承公开故障数据集进行实验。

CWRU滚动轴承实验台如图4所示。

图4 CWRU滚动轴承实验平台

该平台包括一台电机、扭矩传感器、传感器,和型号为SKF 6205的驱动端滚动轴承。轴承的转速为R=1 797 r/min,传感器的采样频率为f=12 000 Hz。

笔者利用电火花技术,人为在滚动轴承表面加工出3种故障,分别是内圈故障、滚动体故障和外圈故障。各故障状态根据故障直径的不同又分为0.177 8 mm、0.355 6 mm、0.533 4 mm的3种故障程度。

在实验中,每种状态都截取数据长度为2 000的60组样本,其中,30组样本作为训练集,剩余30组作为测试集。

实验数据的标签信息详细描述如表1所示。

表1 实验数据

滚动轴承振动信号的时域波形如图5所示。

从图5可以发现:波形杂乱无章,难以直接判断样本的故障类型。

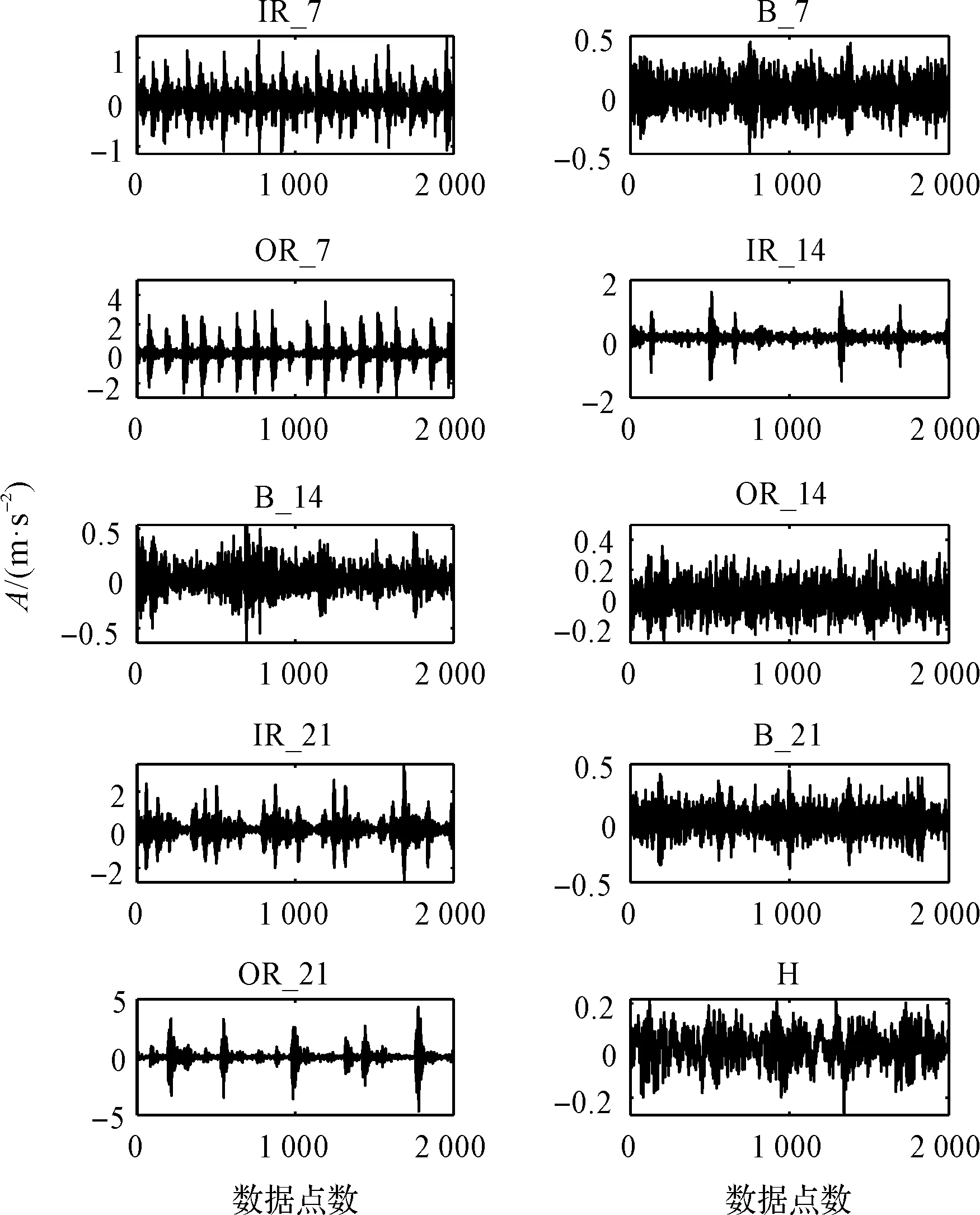
图5 滚动轴承振动信号时域波形

然后,在尺度因子为20时,笔者计算所有滚动轴承的RCMRFDE值。

所有样本第20个尺度的熵值结果,如图6所示。

由图6可以发现:所有故障样本的熵值均大于健康样本,证明了利用基于RCMRFDE和ELM的故障检测方法进行故障检测的可行性。

为了更加直观地确定健康筛选时的阈值,笔者利用式(10)设定了检测阈值,为0.165 9。对比图6可以发现:所有健康样本的熵值均小于该阈值,所有故障样本的熵值均大于该阈值。

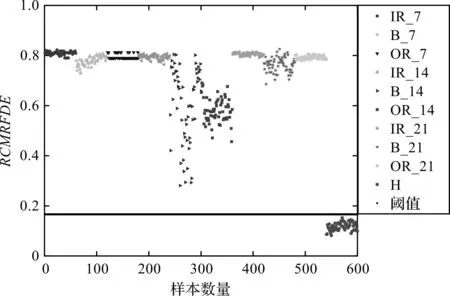
图6 所有样本在尺度τ=20时RCMRFDE分布

由此可见,在检测未知轴承样本时,将其熵值与阈值进行比较,能够快速地判断其健康状态,避免在后续故障特征提取和故障分类过程中,由于模型自身的不确定性而出现错误的分类。因此,通过引入故障检测这一步骤,能够提升模型的可靠性和实用性,避免错误地判断健康轴承的状态。

在完成了健康检测后可知,剩余的轴承样本均存在故障,需要采取模型来识别其故障类型和严重程度。根据流程,笔者利用RCMRFDE提取全部轴承样本的20个尺度的熵值。

4.1.2 对比分析

为了方便对比,笔者分别利用MRFDE、多尺度波动散布熵(MFDE)、多尺度散布熵(MDE)、多尺度模糊熵(MFE)、多尺度排列熵(MPE)进行特征提取。

MRFDE、MFDE和MDE的参数设置与上文一致。对于MFE,嵌入维数m=2,相似容限r=0.2,模糊参数n=2。对于MPE,嵌入维数m=6,时间延迟d=1。

不同熵值方法的特征提取结果如图7所示。

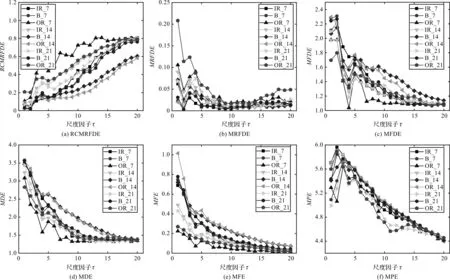
图7 故障轴承的RCMRFDE、MRFDE、MFDE、MDE、MFE和MPE熵值曲线

从图7可以发现:RCMRFDE提取的故障特征具有较好的区分度,在大多数尺度上都具备区分故障的能力,这证明了RCMRFDE能够有效地区分不同故障样本的复杂性;其他5种方法的熵值曲线在一定程度上也能够区分不同故障状态,但部分曲线出现了较为明显的重合,降低了可区分度(例如,MRFDE曲线在尺度因子为5～15部分出现了显著的重叠,此时无法可靠地区分不同故障类型的样本)。

因此,通过对比可以证明,RCMRFDE具有较强的特征提取性能,其采用的复合粗粒化处理具有优于传统粗粒化的性能。

在完成了故障样本的特征提取后,笔者将样本输入至ELM分类器中,再进行样本的训练和识别。

采用基于RCMRFDE和ELM的故障检测方法得到的分类结果,如图8所示。

图8 笔者所提方法的故障识别结果

从图8可以发现:样本的识别准确率达到了100%。可见,所有的故障样本都实现了准确分类,这证明基于RCMRFDE和ELM的方法能够有效地应用于滚动轴承不同故障类型和严重程度的识别。

随后,笔者将采用另外5种对比方法提取到的故障特征输入至ELM分类器,然后进行样本的识别。

采用不同方法得到的故障识别结果如表2所示。

表2 不同方法的故障识别结果

此外,为了验证RCMRFDE在特征提取中的效率,笔者对6种方法的特征提取时间分别进行了记录(其中,电脑环境为MATLAB为2020 a,CPU为i5-10200 H,运行内存为8 GB)。

从表2中可以发现:另外5种方法的准确率均低于RCMRFDE方法,该结果验证了其优越性;

其中,MPE的识别准确率达到了99.26%,仅出现2个错误分类的样本,性能优于除RCMRFDE方法外的其他4种方法。然而,MPE的效率较低,其特征提取的时间需要400 s;

此外,MFDE的特征提取效率最高,仅需要5.38 s即可完成故障特征的提取。这是因为MFDE采用的粗粒化处理,不需要复杂的滑动和平均处理,因此具有较高的效率。

为了进一步验证RCMRFDE在特征提取中的稳定性和优越性,笔者将分别采用6种方法做实验，并重复30次,以有效地避免偶然因素和随机性等未知因素对分类结果的干扰。

采用6种方法的30次分类结果曲线图如图9所示。

图9 30次分类下6种方法的准确率曲线

采用6种方法的30次分类详细结果如表3所示。

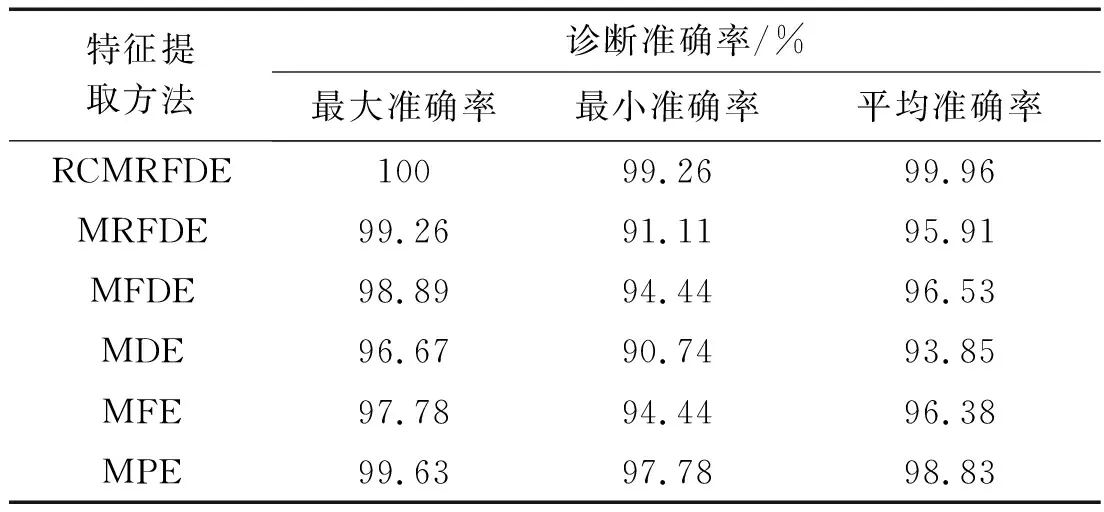
表3 6种方法的30次实验的详细结果

由图9和表3可以发现:采用RCMRFDE方法得到的平均准确率最高,达到了99.96%,明显高于另外采用其它5种方法所得结果,这证明了该方法在多次实验下,仍然能够取得相对可靠的故障识别结果;RCMRFDE的最低识别率为99.26%,即出现了2个样本被错误分类,与图8的结果并不完全一致(这表明单次实验可能不准确,再次验证了多次实验的必要性);

除了MDE外,采用其他4种方法所得的平均准确率均达到了95%以上,也表明这4种方法均能够相对可靠地识别滚动轴承的故障;

综上所述,和其他5种特征提取方法相比,RCMRFDE提取的故障特征具有较高的质量,能获得更加稳定的故障识别结果。

4.2 实验二

4.2.1 实验及分析

在实验二中,笔者利用辛辛那提轴承振动数据来验证RCMRFDE方法的通用性[19，20]。

辛辛那提轴承实验平台如图10所示。

图10 辛辛那提轴承实验平台

笔者将4个轴承布置在驱动轴上(传动轴的转速为2 000 r/min,采样频率为20 kHz),选取了正常、内圈故障、外圈故障和滚动体故障数据分别进行分析,每种数据的具体选择方式参考文献[21]中的方法。

在实验中,针对每种状态,笔者都截取数据长度为2 000的60组样本,其中,30组样本作为训练集,剩余30组作为测试集。

实验数据的详细描述如表4所示。

表4 实验数据的标签信息

滚动轴承振动信号的时域波形如图11所示。

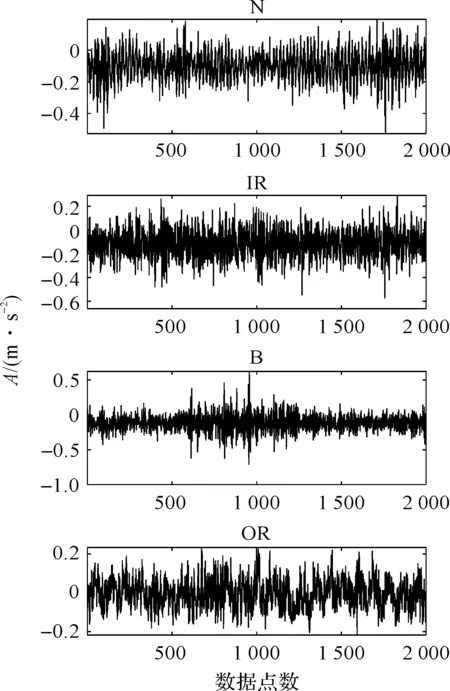
图11 滚动轴承振动信号的时域波形

由图11可以发现:虽然样本B和其他3种信号波形不一致,具有区别于其他3种样本的特点,但是仍然无法完全区分这4种样本。

然后,笔者利用基于RCMRFDE+ELM的故障检测方法来获得该数据下,所有样本的健康阈值。

所有样本的第20个尺度的RCMRFDE熵值如图12所示。

图12 所有样本在尺度τ=20时RCMRFDE分布

由图12可以发现:所有故障样本的熵值均大于健康样本,证明了故障样本的复杂性和健康样本的复杂性之间存在较大的差异,也证明了利用笔者所提方法进行故障检测的可行性。为了更加直观地确定健康筛选时的阈值,设定了检测阈值为0.362,对比图12可以发现,所有健康样本的熵值均小于该阈值。因此,通过引入故障检测这一步骤,能够极大地提升模型的可靠性和实用性,避免错误地判断健康轴承的状态。实验2的故障检测结果也验证了笔者所提模型能够适用于其他轴承数据。

4.2.2 对比分析

随后,笔者利用RCMRFDE、MRFDE、MFDE、MDE、MFE和MPE进行对比,将6种方法提取的故障特征输入至ELM分类器进行识别。

采用不同方法所得的分类结果如表5所示。

表5 采用不同方法所得的故障识别结果

从表5可以发现:RCMRFDE和MRFDE均取得了100%的识别准确率,证明这2种方法都可以有效地诊断轴承的故障;MFDE和MDE均出现了1个样本被错误分类,识别准确率为98.89%,低于RCMRFDE方法;MFE和MPE分别出现了15个和14个样本被错误分类,说明这2种方法不能完全准确地识别样本的故障;

此外,还发现RCMRFDE提取故障特征需要23.68 s,用时比MRFDE和MFDE长,但比MFE和MPE约短1/2,证明了RCMRFDE方法的效率较高。

为了进一步验证RCMRFDE在特征提取中的稳定性和优越性,笔者再次采用6种方法重复实验30次。

采用6种方法所得的30次分类结果的曲线图,如图13所示。

图13 30次分类下6种方法的准确率曲线

采用6种方法所得的30次分类的详细结果,如表6所示。

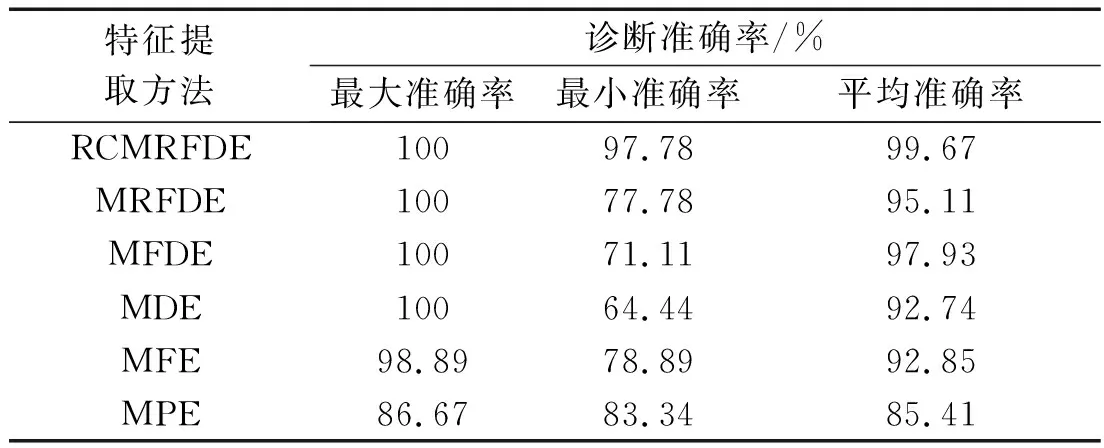
表6 采用6种方法所得的30次实验的详细结果

从图13和表6可以发现:采用RCMRFDE方法所得到的平均识别准确率达到了99.67%,高于其他5种方法,证明了RCMRFDE方法的优越性。

由此可见,即使开展多次实验,采用RCMRFDE方法也能够取得较为稳定的故障识别结果。

5 结束语

为了有效地提升滚动轴承故障诊断的可靠性和准确性,并针对轴承的故障诊断与健康检测,笔者提出了一种基于精细复合多尺度反向波动散布熵(RCMRFDE)和极限学习机(ELM)的滚动轴承综合故障检测方法。

首先,利用RCMRFDE对轴承进行了健康检测,将健康轴承筛选出去;随后,利用RCMRFDE提取故障轴承的特征,反映不同故障的特性;最后,将故障特征输入至ELM分类器进行分类;并采用2种轴承故障实验数据,对该轴承综合故障检测方法进行了实验验证。研究结论如下:

(1)RCMFDE采用了复合粗粒化处理方式,有效克服了MRFDE在处理短时间序列中的不足,减小了分析的误差。RCMRFDE方法能够准确地检测滚动轴承的健康状态,检测精度达到了100%;

(2)RCMRFDE能够有效地提取出滚动轴承振动信号中的故障特征。ELM分类器的分类结果表明,RCMRFDE方法的单次分类准确率达到了100%,即使开展多次分类实验,平均准确率也能达到99.96%和99.67%,优于其他5种对比方法;

(3)基于RCMRFDE方法,提出了滚动轴承综合故障检测方法,避免了盲目的特征提取与模式识别;可以将具备继续服役能力的健康轴承筛选出来,减小了误分类的可能性,增强了设备的工作可靠性。因此,该方法更适合于用于工程中的实际应用。

由于上述实验中所采用的2种数据均为公开数据集,基于RCMRFDE和ELM的故障诊断方法能否有效应用于工业实际尚未得到检验。

因此,在未来的研究过程中,笔者将计划搭建实验平台,以进一步检验上述算法的有效性和其通用性。