基于裂纹扩展的钢桥面板弧形切口疲劳性能研究

杨力

(河南省豫晋高速公路建设有限公司，河南 三门峡 472200)

0 引言

正交异性钢桥面板具有自重轻、承载力大和结构造型美观等优点，被广泛应用于公路、铁路以及城市道路钢结构桥梁中。然而，自1971年英国塞文桥检测出疲劳裂纹以来，钢桥面板的疲劳开裂问题一直未得到有效解决，钢桥面板疲劳研究一直是钢桥领域热点问题[1-3]。钢桥面板构造复杂、连接焊缝较多，疲劳裂纹分布具有一定的随机性，国内外既有的检测信息表明萌生于弧形切口处的疲劳裂纹占所有检出裂纹的50%以上[4]。因此，开展横隔板弧形切口的疲劳性能研究对钢桥面板具有十分重要的工程意义。

弧形切口区域包括纵肋与横隔板交叉连接、横隔板弧形切口，局部构造复杂，且切口处应力集中显著。国内外学者针对钢桥面板弧形切口疲劳性能进行了系统的研究，De Corte[5]通过10个闭口肋弧形切口模型疲劳试验，研究了不同切口形式的应力分布状态，分析了参数变化对细节疲劳性能的影响。唐亮等[6]、王春生等[7]和吉伯海等[8]通过有限元模拟对多种弧形切口形式进行受力分析，研究了疲劳荷载作用下细节疲劳应力幅变化特点及弧形切口参数的影响规律，提出了改善细节疲劳性能的有益措施。高立强[9]采用有限单元法，通过对主拉应力或面外应力比率的变化规律，确定了横梁腹板切口形状对正交异性钢桥面板疲劳性能的影响规律。祝志文等[10]采用名义应力法、热点应力法对细节的疲劳性能进行评估，确定了弧形切口疲劳性能的主要影响因素。张龙威等[11]基于加载测试对比分析了传统沥青铺装和超高性能混凝土(UHPC)铺装的钢桥面板弧形切口受力特性，采用热点应力法对细节疲劳性能进行评估。陈卓异等[12]提出采用切割孔形的方法对已开裂弧形切口细节进行修复，并对切割孔形的圆弧半径、直线长度和倾角进行参数优化。柯璐等[13]和何志刚等[14]分别以钢箱梁桥面板为例，分析了弧形切口的疲劳性能，基于热点应力法对不同切口形式进行对比分析。李爱群等[15]、黄炎等[16]和杜柏松等[17]通过焊接过程和焊缝凝结过程的热力耦合模拟分析，确定了弧形切口区域残余应力分布规律。王春生等[18]和汪珍等[19]通过有限元模拟指出弧形切口细节在残余应力影响下处于“拉—拉”应力状态，并对弧形切口细节裂纹扩展进行了模拟分析。上述研究成果为钢桥面板设计提供了重要的技术支撑，有力促进了钢桥面板的广泛应用。

已开展的研究大多采用名义应力法、热点应力法来表征弧形切口的疲劳性能，而实际工程中弧形切口细节疲劳开裂较为常见，反映出传统疲劳性能表征方法在进行疲劳细节优化设计时效果不太理想。本研究以某三跨斜拉桥为依托，选取国内外典型的弧形切口形式，建立钢桥面板有限元节段模型，研究不同弧形切口形式的残余应力分布，采用扩展有限元方法建立弧形切口细节数值模型，对钢桥面板弧形切口疲劳性能进行研究。

1 弧形切口形式及受力分析

1.1 典型弧形切口形式

早期纵向加劲肋与横隔板连接采用加劲肋与横隔板两侧分别焊接，英国运输和道路研究试验所(Transport and Road Research Laboratory, TRRL)在进行塞文桥加固时采用将横隔板切工艺孔，使得纵向加劲肋连续通过。工程实践表明纵肋与横隔板交叉部位受面内、面外应力的影响，采用纵向加劲肋连续通过的方式可以有效提高细节疲劳强度，目前工程中几乎全部采用此连接方式。

国内外学者对纵肋与横隔板交叉部位疲劳性能开展了大量的研究工作，常用的弧形切口形式如图1所示。形式Ⅰ为欧洲规范[20]推荐的公路钢桥切口形式，形式Ⅱ为美国AASHTO规范[21]推荐形式，切口类似“U”形，采用圆弧进行过渡。形式Ⅲ为实际公路钢桥中使用较多的切口形式，与形式Ⅰ、形式Ⅱ相比切口高度较小，与纵向加劲肋连接的圆弧半径较大，可以有效降低应力集中，被江阴长江大桥、虎门大桥等大型桥梁采用。形式Ⅵ，又称为Haibach形式，欧洲规范建议铁路桥梁采用此切口形式。本研究针对4种常用的公路钢桥面板弧形切口形式，采用扩展有限元方法弧形切口的疲劳性能进行研究。

1.2 弧形切口细节应力分析

某双塔双索面结合梁斜拉桥总体布置如图2(a)所示，跨径布置为(55 000+45 000+220 000+45 000+55 000) mm，结构为半漂浮体系。边跨和部分主跨共109 400 mm采用混凝土箱梁，中跨197 200 mm采用流线型扁平钢箱梁，中间分别设置2 000 mm钢-混凝土结合段。桥面全宽34 500 mm，双向六车道布置，两侧分别设置有3 500 mm宽的人行道。钢箱梁截面如图2(b)所示，中心线高度3 300 mm，两侧风嘴宽度4 197.5 mm，采用工字形开口截面。底板3 855.5、3 583 mm段为直线段，中间采用半径25 000 mm的圆弧过渡。钢箱梁面板采用正交异性板，横隔板间距为3 400 mm。钢箱梁钢板厚度16 mm，顶板闭口加劲肋厚度8 mm，底板12 mm，底板闭口加劲肋厚度6 mm，横隔板厚度12 mm。

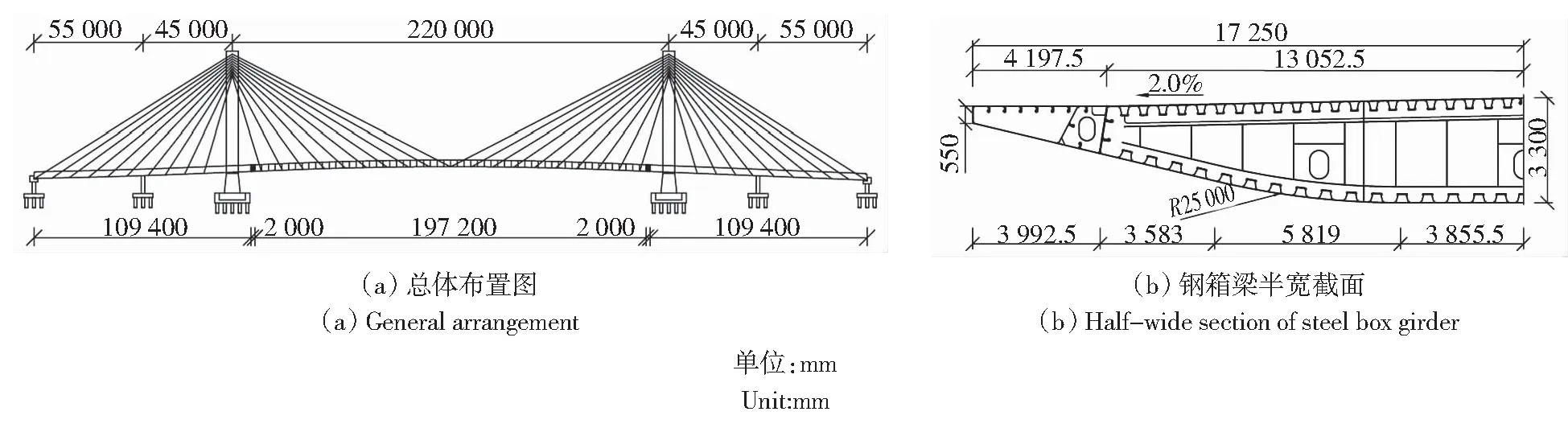
图2 某结合梁斜拉桥Fig.2 A cable-stayed bridge of composite girder

本研究依托实际工程开展弧形切口疲劳性能研究，基于ABAQUS软件建立钢箱梁节段模型和弧形切口实体子模型，如图3所示。节段模型长14 000 mm，包含4个完整的横隔板间距，横向不包括风嘴部分，在进行数值分析时仅变化弧形切口形式，其他参数均保持不变，如图3(a)所示。不同切口形式的实体子模型横隔板高度均取200 mm，完全包含横隔板与纵向加劲肋连接焊缝，加劲肋纵向长度取160 mm，弧形切口细节实体子模型如图3(b)所示。节段模型采用壳单元S4R，实体子模型采用实体单元C3D8R，假定钢材为各向同性、均质的理想弹塑性材料，本构关系采用双折线模型，弹性模量为210 GPa、泊松比为0.3。节段模型横桥向截断位置采用对称约束UZ=RX=RY=0、纵桥向截断位置施加UX=RY=RZ=0，拉索锚固位置约束竖向位移UY=0，对横隔板施加平动自由度约束UX=UY=UZ=0和转动自由度约束RX=RY=RZ=0。实体子模型边界采用ABAQUS软件中“壳-实体耦合”约束与节段壳模型连接。

为满足加载步要求，钢桥面板单元大小划分为100 mm，关注的弧形切口区域实体子模型为2 mm。采用《公路钢结构桥梁设计规范》(JTG D64—2015)[21]中疲劳车辆荷载模型Ⅲ单轴进行加载，轴重120 kN。轮载着地面积按45°扩散，铺装层厚度70 mm，计算得到轮胎实际着地面积740 mm(横向)×

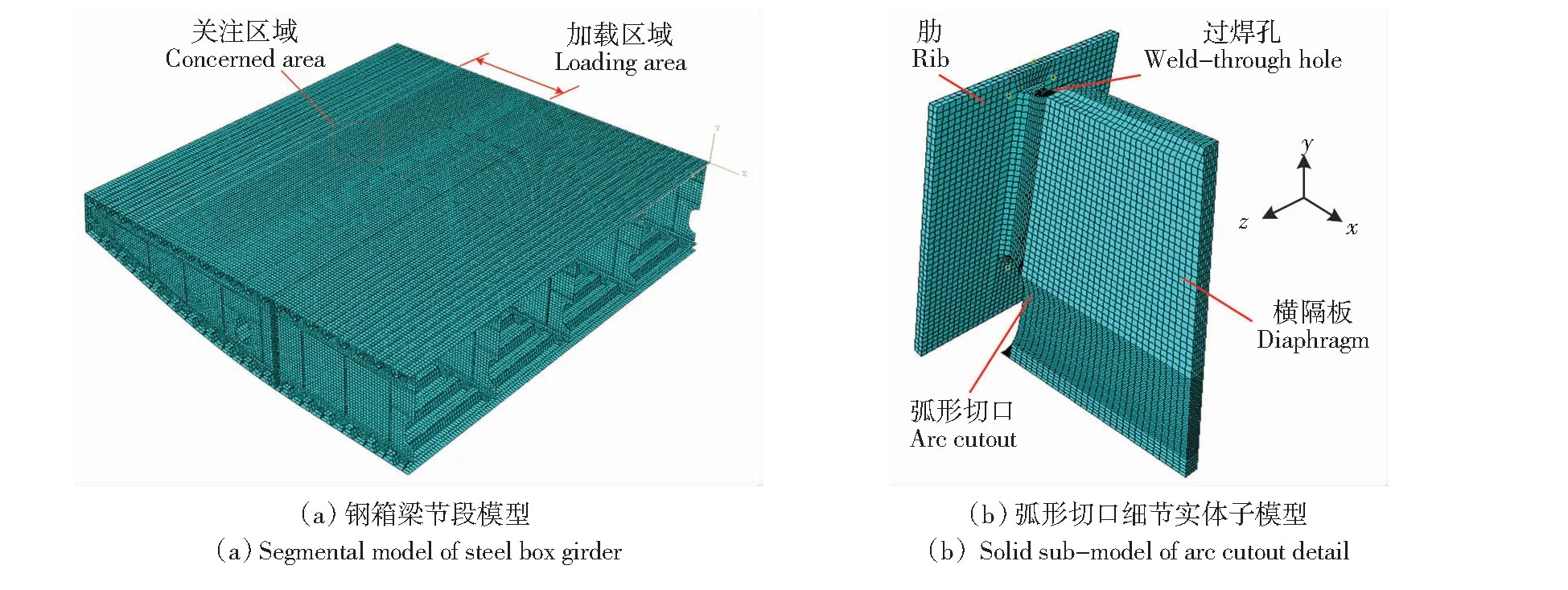
图3 钢桥面板节段模型Fig.3 Segmental model of steel bridge deck

340 mm(纵向)。基于Abaqus软件编制移动加载DLOAD程序，纵向加载步距200 mm、横向加载步距150 mm，共进行345个加载工况(纵向69个、横向5个)。

当车轮荷载中心位于弧形切口细节正上方时，细节疲劳应力最大，以弧形切口Ⅰ为例，细节应力分布如图4所示。弧形切口细节在车辆荷载作用下，细节均处于受压状态，纵肋与横隔板焊趾位置处于受拉状态。当轴载作用在弧形切口细节相邻跨时，细节应力变化显著，轴载纵向位于切口上方时，细节应力达到峰值。弧形切口细节疲劳应力影响线如图5所示，其中切口形式Ⅱ疲劳应力最大，疲劳主应力为87.8 MPa，切口形式Ⅲ疲劳应力最小，疲劳主应力为74.6 MPa。切口形式Ⅰ疲劳主应力为79.0 MPa，切口形式Ⅵ疲劳主应力为81.6 MPa。当轴载移动至距离弧形切口1倍横隔板间距以外时，弧形切口呈受压状态，此时细节疲劳应力较小，4种切口形式拉应力均低于10 MPa。

图4 弧形切口细节应力分布

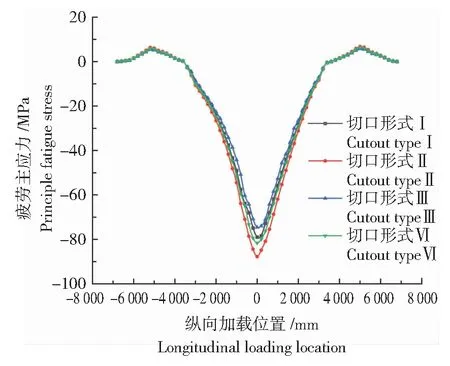
图5 弧形切口细节疲劳应力影响线Fig.5 Fatigue stress of arc cutout detail

2 弧形切口细节残余应力分析

弧形切口细节在轮载作用下均处于受压状态，一般认为不会萌生疲劳裂纹或初始裂纹处于闭合状态。然而，基于实桥检测结果弧形切口区域疲劳裂纹较多[3]，已成为钢桥面板主要的疲劳开裂细节。文献[15]采用参数化建模，对横隔板与纵向加劲肋焊接过程进行模拟，确定了弧形切口区域存在较高的残余应力场。为开展钢桥面板弧形切口细节疲劳裂纹扩展分析，本研究建立热弹塑性有限元模型，对不同切口形式的残余应力分布进行研究。

2.1 焊接模拟有限元模型建立

横隔板与纵向加劲肋采用双面角焊缝连接，焊接过程模拟分为2个阶段，先进行一侧焊缝模拟，待焊接区域温度冷却至环境温度，再进行另一侧焊缝模拟。本研究采用顺序耦合分析法进行残余应力分析，利用传热单元模拟焊接过程的温度场分布，将温度场作为外荷载施加到力学求解有限元模型上，进行热力耦合分析，最终确定焊接残余应力场。在钢桥面板节段壳模型中，建立弧形切口细节的局部实体子模型，如图3(b)所示。

焊接温度场分析采用DC3D8八节点线性六面体传热单元，残余应力分析采用C3D8R单元。焊接温度场与残余应力场模拟时，网格需完全一致，实体子模型网格大小为5 mm。切口形式Ⅰ模型共6 334个单元，切口形式Ⅱ模型共6 264个单元，切口形式Ⅲ模型共6 498个单元，切口形式Ⅵ模型共6 780个单元。焊接热分析时，设置实体子模型与空气接触面均为散热面，残余应力分析时，约束纵肋和横隔板顶、底部竖向位移Uy=0，横隔板横向边界施加x方向对称约束Ux=Ry=Rz=0，在纵肋腹板的纵向两端施加纵向位移约束Uz=0。采用“生死单元法”模拟焊缝的形成，编制移动热源子程序DFLUX实现热源模型移动，热源模型采用双椭球体热源模型。钢材的导热系数、比热容、对流换热系数等常数参照文献[18]选用。

2.2 焊接残余应力分析

焊接完成后冷却至常温状态，弧形切口细节的残余应力分布如图6所示。焊缝周围焊接残余应力峰值达到Q345qD的屈服强度，受弧形切口形式的影响残余应力分布规律差异显著。切口形式Ⅰ、Ⅱ、Ⅵ的残余应力影响范围更广，在横隔板-纵肋焊趾周围产生较大影响，切口形式Ⅲ影响范围较小，且残余应力峰值明显小于其他切口形式。弧形切口区域受焊接过程影响，残余应力沿切口周边呈现非线性变化趋势，且均为拉应力。

图6 弧形切口细节焊接残余应力分布Fig.6 Welding residual stress distribution of arc cutout detail

为验证焊接残余应力模拟的准确性，选取横隔板与纵肋连接焊缝焊接路径上焊接残余应力分布，并与实测数据进行对比，如图7所示。文献[22]针对弧形切口形式I采用盲孔法进行焊接残余应力测试，沿焊缝方向(y方向)残余应力与本研究模拟结果误差小于10%，可以认为本研究弧形切口区域焊接残余应力模拟结果准确。不同弧形切口形式的焊接方向上残余应力分布规律基本一致，在起弧和熄弧阶段残余应力变化剧烈，焊缝中部残余应力达到峰值且波动较小。以横隔板-纵肋连接焊缝焊趾处为原点，焊接方向上起弧50 mm范围内残余应力增大至300 MPa以上，然后基本保持不变。不同切口形式的焊缝长度略有差异，熄弧阶段残余应力变化较起弧阶段更为显著，距离焊缝末端30 mm左右，焊接残余应力由峰值降至较低水平。

为研究弧形切口细节疲劳裂纹扩展规律，选取弧形切口边缘单元应力，对弧形切口区域残余应力进行分析，如图8所示。4种弧形切口形式焊接残余应力均为拉应力，自横隔板焊趾处起呈现出先增大、后减小的变化趋势，受弧形切口形式的影响，残余应力的变化趋势略有差异。切口形式Ⅰ、Ⅱ在距离焊趾10 mm处残余应力最大，Von Mises应力(基于剪切应变能的一种效应力)峰值分别为215、243 MPa。切口形式Ⅲ、Ⅳ在距离焊趾15 mm处残余应力最大，Von Mises应力峰值分别为262、274 MPa。切口形式Ⅵ残余应力峰值最大，切口形式I最小，距横隔板焊趾位置50 mm处残余应力均低于100 MPa。考虑焊接残余应力与疲劳车辆荷载的共同作用，则弧形切口细节均处于受拉状态。

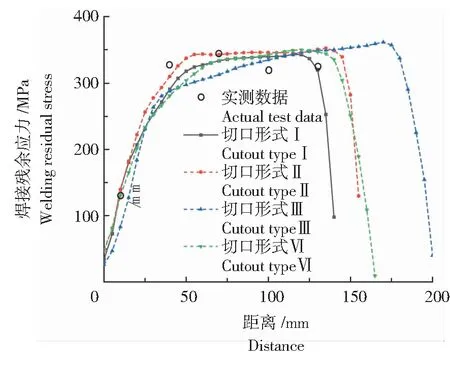
图7 横隔板-纵肋连接焊缝残余应力分布 Fig.7 Residual stress distribution of diaphragm-to-rib welding joint

图8 弧形切口细节残余应力分布Fig.8 Residual stress distribution of arc cutout detail

3 弧形切口疲劳性能研究

3.1 弧形切口疲劳裂纹扩展模拟

为研究钢桥面板弧形切口细节疲劳性能，考虑焊接残余应力与疲劳车辆荷载耦合作用，对弧形切口细节疲劳裂纹扩展进行模拟分析。疲劳裂纹扩展采用扩展有限元法进行模拟，在裂纹扩展过程中无须进行网格重新划分，计算效率较高且精度能够满足工程需求[23]。

建立含初始裂纹的弧形切口细节局部实体子模型，在弧形切口边缘最大主应力处设置初始裂纹，采用直接循环法进行疲劳裂纹扩展模拟。为计入焊接残余应力，疲劳裂纹扩展模拟子模型与残余应力分析模型完全一致，采用初始应力法引入残余应力。初始裂纹采用1/4椭圆进行模拟，a0/c0=5 mm/6 mm(a0表示椭圆半短轴长度，c0表示椭圆半长轴长度)。根据弧形切口细节受力分析结果，选取最不利荷载作用工况进行疲劳裂纹扩展分析，荷载工况如图9所示。疲劳荷载模型Ⅲ双联轴纵向分别位于目标细节的两侧，横向单侧轮胎中心位于弧形切口细节上方，单侧轮胎作用面积为740 mm(横向)×340 mm(纵向)。

图9 疲劳裂纹扩展模拟加载工况Fig.9 Loading case for fatigue crack propagation simulation

疲劳裂纹扩展判定与描述是开展疲劳性能分析的关键，常用的疲劳裂纹扩展公式有Paris公式、Forman公式等。本研究主要针对弧形切口疲劳裂纹扩展的第Ⅱ阶段进行研究，钢材疲劳裂纹扩展本构模型采用Paris公式

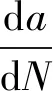
(1)

式中：a为裂纹长度，mm；N为循环次数；Δk为应力强度因子幅；C和m为材料常数。

由于弧形切口细节疲劳性能受局部构造、横隔板面外变形的影响，疲劳裂纹多为复合型，在进行疲劳裂纹扩展分析时选取应变能释放率定义裂纹的复合断裂准则

(2)

ΔGe=ΔGⅠ+1.9ΔGⅡ+2.1ΔGⅢ。

(3)

式中：GⅠ、GⅡ和GⅢ分别为Ⅰ、Ⅱ和Ⅲ型裂纹在扩展过程中的应变能释放率；Gth为应变能释放率门槛值；ΔGe为等效应变能释放率幅值。

基于线弹性断裂力学理论，应变能释放率(G)与应力强度因子(K)存在对应关系，见公式(4)。

(4)

式中，E为材料弹性模量。

在进行疲劳裂纹扩展模拟时，Paris公式可以采用应变能释放率表示

(5)

式中，c1，c2为材料参数。当裂纹尖端应变能释放率满足ΔGe≥Gth时，裂纹开始扩展。

3.2 弧形切口细节疲劳性能分析

考虑焊接残余应力与疲劳荷载共同作用，弧形切口细节疲劳裂纹扩展模拟共进行1 000万次循环加载计算，疲劳裂纹扩展形态如图10所示。加载初期疲劳裂纹均沿着初始方向扩展，随着循环次数的增加，裂纹逐渐向横隔板内部发展。弧形切口形式Ⅰ、Ⅲ裂纹扩展趋势基本一致，裂纹沿初始方向扩展，切口形式Ⅰ在循环加载400万次后向横隔板内部偏转角度增大。切口形式Ⅱ在加载至100万次后向横隔板内部偏转角度增大，之后扩展角度基本保持不变。弧形切口形式Ⅵ在0～200万次循环加载过程中裂纹沿初始裂纹方向扩展，循环加载至300万次时裂纹扩展方向基本与横隔板-纵肋连接焊缝平行，500万次循环加载后裂纹扩展方向进一步向焊缝方向偏转。循环加载1 000万次后，切口形式Ⅰ裂纹扩展路径最短，切口形式Ⅵ裂纹扩展路径最长，且裂纹扩展路径向焊缝偏移，对横隔板-纵肋连接细节的局部刚度降低影响较大。切口形式Ⅱ、Ⅲ疲劳裂纹扩展长度居中，其中切口形式Ⅱ裂纹长度明显大于切口形式Ⅲ。

图10 弧形切口细节疲劳裂纹扩展形态Fig.10 Fatigue crack propagation state of arc cutout detail

为了进一步研究弧形切口细节疲劳裂纹类型与扩展规律，以切口形式Ⅵ为例，不同类型裂纹的应变能释放率如图11(a)所示。弧形切口细节裂纹以Ⅰ型(张开型)裂纹为主，扩展过程中Ⅱ型(滑开型)裂纹、Ⅲ型(撕开型)裂纹应变能释放率约为Ⅰ型裂纹的13%。Ⅱ型裂纹、Ⅲ型裂纹与横隔板平面外变形密切相关，在弧形切口细节疲劳裂纹扩展过程中起到改变裂纹方向的作用。不同弧形切口形式的累计等效应变能释放率如图11(b)所示。从开始加载至300万次期间，切口形式Ⅱ累计等效应变能释放率远远高于其他3种切口形式，0～180万次加载过程中切口形式Ⅲ、Ⅵ累计等效应变能释放率较低，即裂纹扩展速率较慢。340万次循环加载后，切口形式Ⅵ扩展速率明显加快，累计等效应变能释放率显著高于其他3种切口形式。切口形式Ⅰ疲劳裂纹扩展速率相对较慢，累计等效应变能释放率较低，在420～580万次扩展速率明显加快，之后扩展速率保持较低水平。1 000万次加载完成后，切口形式Ⅵ累计等效应变能释放率最大，切口形式Ⅲ、Ⅱ次之，切口形式Ⅰ最低。

图11 弧形切口细节裂纹扩展应变能释放率Fig.11 Strain energy release rate of crack propagation in arc cutout details

结合不同弧形切口形式疲劳裂纹扩展形态与累计等效应变能释放率对比结果，切口形式Ⅰ疲劳性能最优，切口形式Ⅲ、Ⅱ次之，切口形式Ⅵ疲劳性能相对最差。4种弧形切口形式中，切口形式Ⅵ切口面积最大，车辆荷载作用下弧形切口区域平面外变形增大，使得疲劳裂纹扩展速率加快。切口形式Ⅲ切口高度明显小于其他切口形式，而切口半径大于其他切口形式，结合细节疲劳应力分析结果表明切口半径增大可以有效降低疲劳应力水平。对比分析切口形式Ⅰ、Ⅱ，弧形切口下部采用半径较大的圆弧过渡能够降低细节疲劳应力、提高该细节的疲劳性能。因此，在进行钢桥面板弧形切口细节设计时，应充分考虑焊接残余应力的影响，根据不同切口形式的疲劳性能选取合理的构造形式。

4 结论

本研究以某三跨斜拉桥为工程背景，建立钢桥面板有限元节段模型和弧形切口细节实体子模型，实现横隔板-纵肋连接焊缝的全过程模拟，确定不同弧形切口形式的残余应力分布，基于疲劳裂纹扩展对钢桥面板弧形切口疲劳性能进行研究。得到如下主要结论。

(1)疲劳荷载作用下弧形切口细节受压，焊接残余应力在弧形切口区域峰值达200 MPa以上，沿弧形切口方向呈现出先增大后减小的变化趋势，考虑疲劳荷载与残余应力共同作用时，弧形切口细节处于受拉状态。

(2)疲劳荷载与残余应力共同作用下，弧形切口细节疲劳裂纹先沿着初始裂纹方向向横隔板内部扩展，之后产生不同程度的偏转，Haibach形式疲劳裂纹向横隔板-纵肋连接焊缝方向扩展。

(3)欧洲规范推荐切口形式疲劳性能最优，实际公路钢桥常用切口形式与AASHTO推荐形式次之，Haibach形式疲劳性能相对较差。

(4)在进行钢桥面板弧形切口细节设计时，应充分考虑焊接残余应力的影响，根据不同切口形式的疲劳性能选取合理的构造形式。