基于支持向量聚类和模糊粗糙集的交通流数据修复方法
朱世超,王骋程,王超,刘隆,张润芝,3,王浩,3
(1.山东高速基础设施建设有限公司,济南 250000;2.山东省交通规划设计院集团有限公司,济南 250000;3.山东高速济潍高速公路有限公司,济南 250000)
0 引言
环路检测器与视频、蓝牙和装有全球定位系统(Global Positioning System, GPS)设备的浮动车辆等传统的交通数据收集方法相比,其检测成本低的优势在交通流量数据检测中被广泛使用。然而,这些技术检测出来的数据可能会由于天气因素、数据传输中的延迟和错误,以及数据丢失等因素的影响[1-4]而出现数据异常、缺失等情况。交通流数据的完整性是交通流预测、交通运行状态分析和路网通行能力分析的基础,交通数据的缺失必将影响分析结果的合理性及其在智能交通系统(Intelligent Transportation System, ITS)中应用的可行性[5]。因此,如何从庞大的交通大数据系统中获得真实、准确的信息来反映交通状态是研究者们目前面临的重要问题。
为提高交通模型输入数据的准确性,国内外学者建立了许多模型对交通数据进行预处理。当前,国外关于数据修复方面的研究可以归纳为4个方面,分别以传统模型、统计相关模型、机器学习模型和粗糙集模型为基础。传统方法的结构简单且易于计算,估计性能主要取决于交通流数据中的相似性特征,然而交通流的短期波动表现使得相似性并不显著,因此传统方法的估算性能常常不尽如人意;与传统方法相比,统计模型通常以其合理的数学结构表现出良好的归因性能,并且在交通流分析中具有清晰的可解释性,因此被广泛用于数据插补中;基于机器学习的插补方法在数据不完整的情况下由于其强大的学习能力而表现出较高的归因或预测性能,也成为了一种典型的交通流缺失数据处理方法;以粗糙集模型为基础的数据修复方法,其中模糊粗糙集(Fuzzy Rough Set, FRS)是在数据集不完整的情况下进行分类和预测的有效方法[6-9]。模糊粗糙集融合了粗糙集和模糊集的优势,通常表现出较强的能力来表示原始数据集中的不确定性和模糊性。然而,无监督学习机制使得模糊粗糙集的学习能力相对有限,导致其应用的推算或预测结果可能并不理想。一些神经模糊推理系统是为分类而设计的,很少有方法可以使用该系统来估算缺失的数据[10-12]。
在国内方面,随着交通智能化的不断发展,数据质量的问题引发了越来越多研究人员的关注。国内相关学者认为,首先应该充分了解数据丢失的过程,然后根据数据丢失的形式采取对应的修复模型。针对不同情况的数据缺失,选择不同的数据修复方法及模型可以更好地提高修复的准确度[13-14]。此外,交通流数据之间的空间相关性逐渐受到重视。邹海翔等[15]利用插值法对交通数据进行空间建模,以空间距离作为度量基准对未知路段交通数据进行估计。一些学者同样在探索使用基于粗糙集的修复方法以提高数据质量。于洪等[16]考虑具有不同丢失值的数据的相关性,结合粗糙集理论提出了一种基于时空权重的交通流数据的重构模型,利用北京二环高速公路的数据完成了仿真建模。
尽管目前大量工作侧重于对丢失的交通流数据进行插补,但是如何快速准确地估计丢失值,尤其是在高丢失率下,仍然是在ITS应用中实现交通流精确预测和合理分析的挑战。为了克服交通数据中强随机性对插补性能的影响,将机器学习框架和交通流理论相结合被证明是提高插补精度的有效方法[17-18]。在神经网络插补的应用中,训练过程中的参数选择和优化是实现较高插补性能的关键步骤[18-19]。当支持向量机(Support Vector Machine, SVM)模型用于缺少的流量估算时,也需要解决类似的问题[21-22]。与神经网络相比,支持向量机具有更好的拟合性能和泛化能力。因此,本研究将支持向量聚类和模糊粗糙集相结合,并结合模糊神经网络和遗传算法建立了一个混合模型来估算丢失的交通流数据,结合粗糙集和神经模糊系统的混合模型可以在不完整的数据集下训练模型,并可以估计缺失值的近似间隔。该混合模型结合粗糙集处理不确定性的优点和在神经模糊网络中具有监督学习过程的强大学习能力,并增强了图像识别中的聚类性能。因此,可以提高交通流数据中缺失值估算的准确性和稳定性。最后以高速公路的实测交通流数据为例对模型的性能进行验证。
1 粗糙支持向量聚类分类模型
1.1 粗糙集
粗糙集理论提供了一种依靠模糊和不精确的数据推理的技术,由Pawlak[23]于1982年提出。从可用信息的角度来看,具有相同信息的对象是不可分辨的。由不可分辨的物体组成的基本集形成了知识的基本粒子。基本集合的联合被称为清晰集合,否则该集合被认为是粗糙的。

(1)
(2)
式中:X为研究的论域;x为X中的一个对象;[x]R表示所有与x不可分辨的对象所组成的集合;Ø为空集。
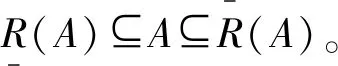
粗糙度是指上部和下部近似之间的差异,集合A的粗糙度是通过等价关系R来定义的,定义如下。
(3)
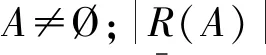
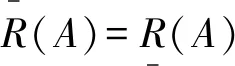
1.2 支持向量聚类
在支持向量聚类中[24],用核函数变换实现将数据点从平面空间映射到高维的特征空间。在高维特征空间上,寻找囊括所有数据点的最小空间球体。然后将此球映射到平面空间,则它将形成一些可以包围数据点的形状。内核参数可以控制群集的数量。在这里,借助软边距公式来处理异常值。
为了定义公式,令{xi}⊆X是具有m个点的多维数据集,数据空间为xi∈Rd。使用从X到某个高维空间的非线性变换φ,寻找包含X的所有点的最小半径R的球体。原始问题表达公式为
(4)

由于这是一个凸二次规划问题,因此很容易解决它的Wolfe对偶形式
s.t. 0≤∂i≤Ci=1,2,…,m;
(5)
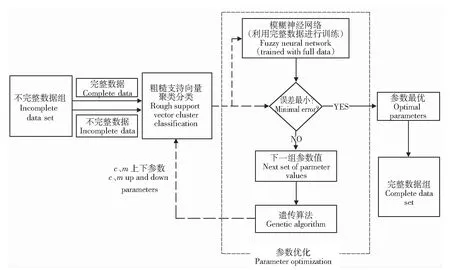
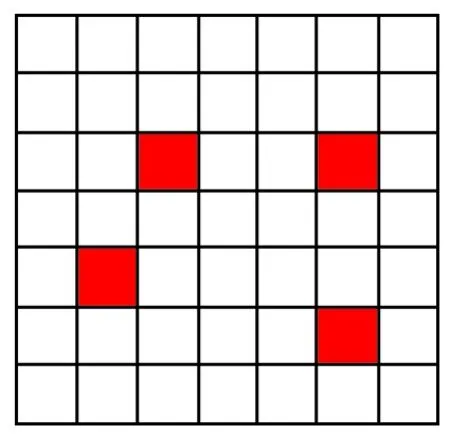
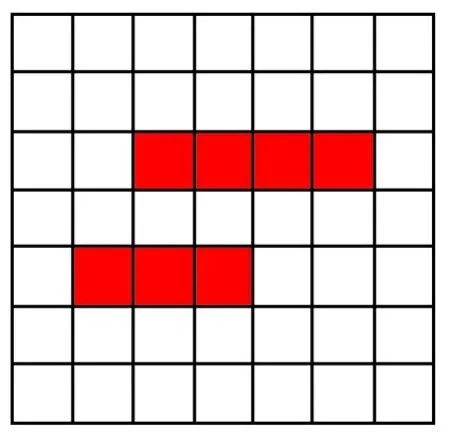
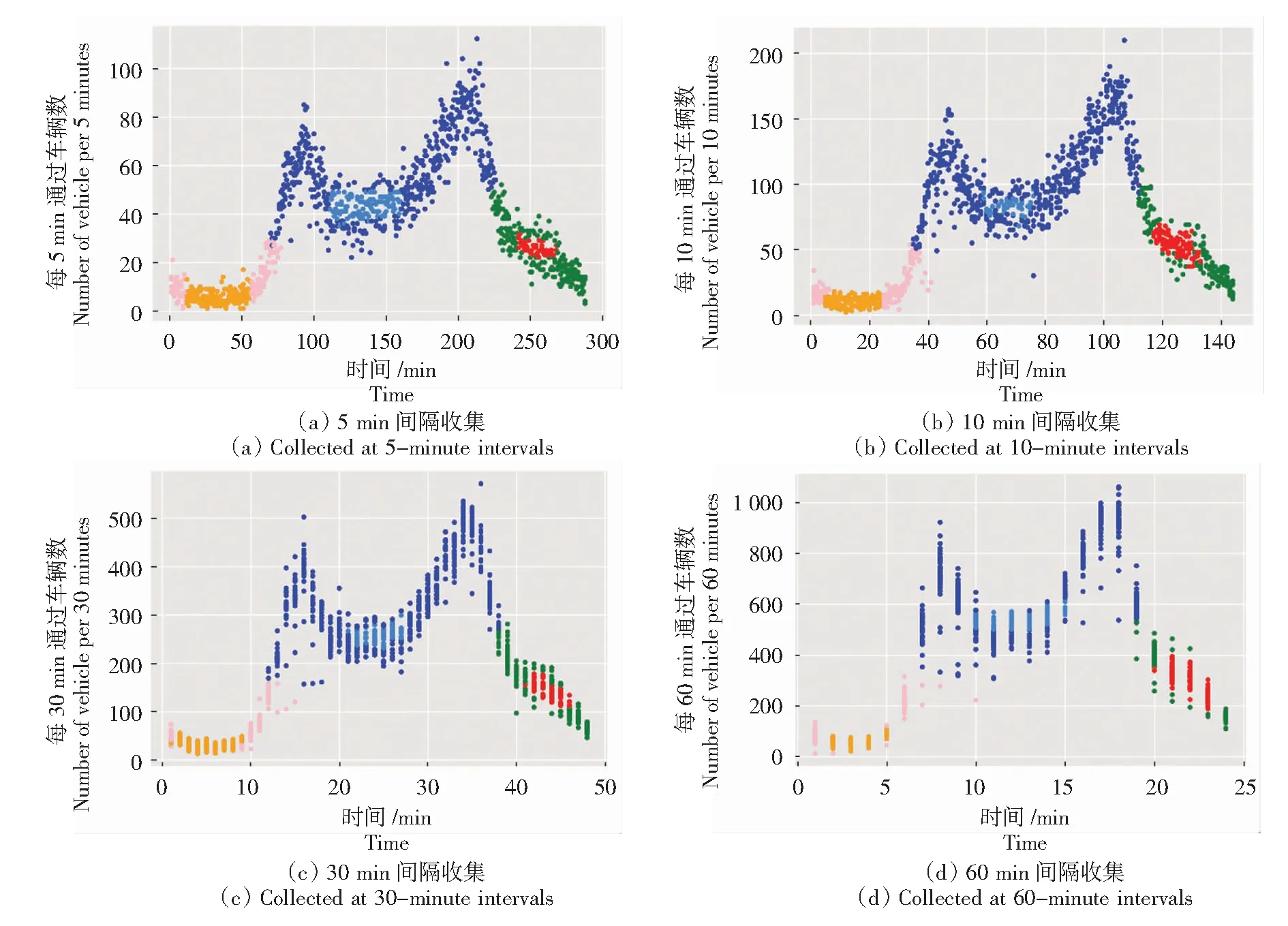
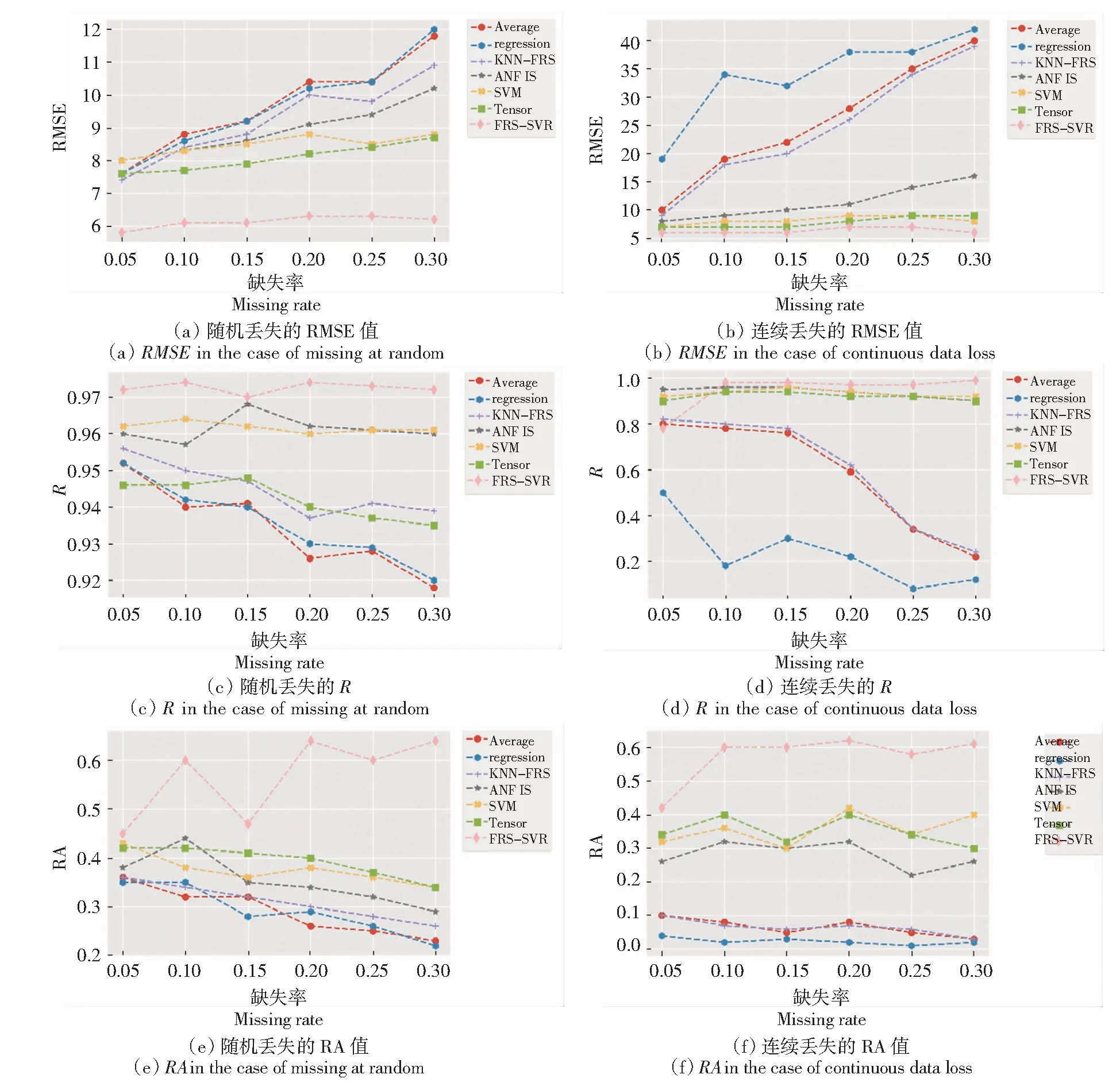
式中:K(xi,xj)表示核函数,给出了高维空间中的点积φ(xi)·φ(xj);∂i的值决定点φ(xi)是在球体内还是球体外;0<∂i R={G(xi):0<∂i (6) 现在,由{x/G(x)=R}定义了包围数据空间中点的轮廓。因此,借助核函数,避免了在高维空间中进行计算以及在数据空间中查找轮廓的反向映射。一旦找到这些轮廓,就按以下步骤完成聚类分配。根据观察结果,其采用涉及G(x)的几何方法:给定一对属于不同聚类的点,连接其任何路径都必须从特征空间的球体中退出。因此,可以通过将其连接在特征空间中的球面之中或之上的点xi和xj对之间定义邻接矩阵M,将其连接到的路径的图像定义为 (7) 式中,y表示xi,xj连线上的点;∀表示为对任意的属于xi,xj连线上的点y。 将聚类定义为由M诱导的图的连接部分,可以将球外的点(有界支持向量)分配给最接近的聚类。 在支持向量模型的基础上,遵循粗糙集的概念,粗糙球体为具有下近似的内半径(R)和上近似的外半径(T),并且T>R的球体。与支持向量聚类(Support Vector Clustering, SVC)中一样,粗糙支持向量聚类(Rough Support Vector Clustering, RSVC)还通过使用内核函数来实现平面数据映射到高维空间。其试图在高维空间中找到内外半径最小的粗糙球体,将数据集中所有点的图像封闭起来。现在,那些图像位于较低近似范围内的点是肯定属于一个群集(群集的核心)的点,而图像位于边界区域(位于较高近似范围内但不在较低近似范围内的那些点)被称为由多个群集(群集的软核)共享。某些点被允许位于球外,被称为离群值。 利用非线性变换方法,将数据从平面映射到某些高维空间,寻找内近似半径(R)和外近似半径(T)的最小封闭粗糙球体。原始问题表达公式为 0≤ξi≤T2-R2,ξi′≥0,i=1,2,…,m。 (8) 为了解决这个问题,找到在SVC中的Wolfe对偶形式,所以拉格朗日可以写成 (9) 式中:αi≥0,βi≥0,λi≥0,ηi≥0 ,i=1,2,…,m。 应用KKT条件,可以得到 (10) (11) (12) (13) 补充松弛条件为 (14) λi(ξi-T2+R2)=0。 (15) βiξi=0。 (16) ηiξi′=0。 (17) 从以上等式可以将Wolfe对偶形式写为 (18) 可以观察到,当δ>1,采用RSVC公式;当δ=1时,其退化为原始SVC公式。 从公式(12)和公式(13)可以看出,αi的值决定了图案xi是否落在较低近似值,边界区域或特征空间粗糙球之外。 其来自表示点的图像公式(12)—公式(18)。 (1)αi=0处于较低近似值。 第二步:查找图形的连接组件。通过查找图形的连接组件,给出每个簇的较低近似值。 第三步:寻找边界区域。对于任何聚类j,对于xi∈下近似(Ci)和xk∉下近似(Cj):G(y)≤T,∀y∈[xi,xk],则xk∉边界区域(Ci)。 模糊推理系统[25]基于模糊规则库实现模糊推理。通常规则表示为 Rr:如果x是Ar,那么y是Br。 (19) 式中:x是对象或状态;y=[y1,y2,…,ym]是输出语言变量;Ar是规则r的前置部分使用的模糊集;Br是规则r后置中使用的模糊集;r=1,…,N;N是规则数;m是输出语言变量的数。 假设ε=[ε1,ε2,…,εn]是描述任何对象或状态的特征的向量,n是输入语言变量的数量。将对象的隶属函数及其特征等同起来,可以将规则(19)记为 Rr:如果ε是Ar,那么y是Br。 (20) (21) (22) 接下来枚举几组模糊蕴含 S-模糊蕴含:I(a,b)=S{N{a},b}; R-模糊蕴含:I(a,b)=supz∈[0,1]{z|Г{a,z}≤b}; QL-模糊蕴含:I(a,b)=S{N{a},Г{a,b}}; D-模糊蕴含:I(a,b)=S{Г{N{a},N{b}},b}。 其中a,b∈[0,1],Г是任何t-范数,S是任何t-范数,N是任何模糊否定。 将模糊推理模型和神经网络系统进行集计可以构成模糊神经网络[21-22](Fuzzy Neural Network, FNN),实际上是将常规的神经网络模型输入模糊的信号和权值,其结构如图1所示。 图1 标准模糊神经网络结构Fig.1 Structure of a standard fuzzy neural network 将模糊推理系统与自适应神经网络集计在一起,该组合系统更加可以发挥这2个模型的优势,弥补了这2个模型的不足。该系统的框架如下。 第1层:通过计算输入信号的隶属函数的值来模糊输入信息,一般模型使用的隶属度函数是高斯函数,其计算公式为 (23) 式中:xa是节点a的输入;高斯函数的形状由参数c和b决定,c、b分别是隶属函数形状的中心值和宽度,被称为前件参数。 第2层:强度释放层。变量x与模糊集A的隶属度定义为 μA(r)(X)=μa1(r)(x1)·μa2(r)(x2)…μaA(r)(xA)=∑a∈Aμa(r)(xa)。 (24) 式中,r是模糊规则。 第3层:对所有规则信息强度进行归一化处理操作。在神经网络的每个节点处根据模糊规则r下计算归一化可信度 (25) 式中,R是规则库。 第4层:计算在模糊规则r下的每个节点的输出信号。第4层的每个输出信号均是拥有自适应性质的节点,其输出结果为 f(r)(X)=g(r)(X)·y(r)(X)。 (26) y(r)(X)=pT·[1,X]T=[p0(r),p1(r),…,pA(r)]·[1,x1,…,xA]T。 (27) 其中,g(r)(X)是第3层归一化可信度的输出;p是第4层上每个节点的参数集,称为后置参数。 第5层:计算所有信号的总输出。该层是一个固定节点,其计算如下 (28) 在利用粗糙支持向量聚类进行数据分类之后,获得了各个分类的上下中心,然后结合模糊神经网络和遗传算法进行缺失数据的补齐,具体的修复步骤如下。 (1)使用模糊神经网络训练完整数据集,输入数据组X,输出的数据组为Y。 (3)使用遗传算法获得优化的参数c和m,最小化粗糙支持向量与模糊神经网络两者输出之间的差异,使用带有优化参数的支持向量补齐缺失。 (4)将结果与模糊神经网络输出的结果进行对比。 本研究建立的模型框架如图2所示。该框架由3个模块组成。首先,通过粗糙集和支持向量聚类相结合来进行交通流数据的分类,设定初始的上下c、m参数,利用加权因子法获得缺失数据的补齐值。然后,利用模糊神经网络进行数据的预测获得的数据与前面的数据进行对比,然后利用遗传算法优化参数,减小修复误差,获得最优参数。 本论文使用的交通流数据是高速公路上利用线圈探测器采集的交通量数据,共计120 d,时间是2011年1月至2011年4月。在图3中显示了1月3日至1月7日不同时间间隔(5、10、30、60 min)的交通流量数据分布。 根据缺失的位置的分布情况,可以将数据缺失形式分为随机丢失、连续丢失和系统丢失,3种丢失形式的示意图如图4所示。 图2 基于支持向量聚类和模糊粗糙集的交通流数据修复框架图Fig.2 Framework of missing data imputation for traffic flow based on SVC and fuzzy rough set 图3 在相邻的5 d内以不同的时间间隔收集的流量数据折线图Fig.3 Graphs of traffic data collected at different time intervals during the five adjacent days 利用建立的粗糙支持向量聚类模型进行交通流数据的分类,在数据以不同时间间隔收集的情况下获得的分类结果如图5所示。 在图5中,交通流数据总共分成了3类,分别以橙色、蓝色和粉色为中心,球形的上近似半径和下近似半径形成了轮廓包围了这3个中心。可以通过设置每个分类的上下中心的权值,通过加权平均值法获得初始缺失数据补齐值。 (a) 随机丢失(a) Missing at random (b) 连续丢失(b) Continuous data loss (c) 系统丢失(c) Systematic data loss 图5 粗糙支持向量聚类模型分类结果图Fig.5 Classification results of the support vector clustering model with fuzzy rough sets 在进行数据分类之后,结合模糊神经网络和遗传算法对缺失数据进行补齐,选取均方根误差(RMSE)、相关系数(R)、相关精度(RA)3个结果评价指标,并选择平均值法(MV)、回归法(Regression)、基于KNN的模糊粗糙集方法(KNN-FRS)、自适应网络的模糊推理系统(ANFIS)、支持向量机(SVM)和张量(Tensor)6个模型进行结果对比。在数据以5 min间隔收集,以不同丢失形式,不同丢失率的情况下,结果如图6所示。 从图6可以看出,在随机丢失和连续丢失2种情况下(本研究中的数据丢失是对采集的完整数据集进行随机丢失和连续丢失的模拟),随着数据丢失率的增加,模型的补齐结果的均方根误差(RMSE)都增加,相关系数(R)和相对精度(RA)都减少,说明随着数据丢失率的增加,模型的补齐效果减少。通过图6(a)和图6(b)可以看出,随着丢失率增大,基于支持向量聚类和模糊粗糙集的交通流数据修复方法(FRS-SVR)的结果均小于其他6种方法,这说明就均方根误差这一评价指标而言,本研究所建立的交通流丢失数据补齐模型的修复效果优于其他6种对比模型。通过图6(c)和图6(f)中关于指标相关系数和相对精度的结果可以看出,随着数据丢失率的增加,基于支持向量聚类和模糊粗糙集的交通流数据修复方法(FRS-SVR)的结果从总体上来说均大于其他6种方法,这说明根据相关系数和相对精度这2个评价指标的表现,本研究所建立的交通流丢失数据补齐模型的修复效果优于其他6种对比模型。 图6 在不同丢失类型的数据集中7种方法的性能表现Fig.6 Performance of seven methods in datasets with different missing strategies 本研究将支持向量聚类和模糊粗糙集相结合,并结合模糊神经网络和遗传算法建立了一个混合模型来估算丢失的交通流数据。将模糊粗糙集和支持向量聚类结合,进行不同时间间隔收集的交通流数据的分类,然后结合模糊神经网络和遗传算法进行缺失数据的估计。利用某高速公路收集的交通流数据用于模型性能的验证,并使用均方根误差、相关系数和相关精度3个指标来评估插补精度。结果表明,研究中提出的支持向量聚类和模糊粗糙集模型的插补性能比其他6种对比方法的修复性能更高。这些结果验证了所提出的方法的有效性,也呈现出一定的局限性。例如,随着缺失率的增加,3个评价指标的恶化程度迅速增加,这意味着模型的补齐效果降低,模型的稳定性较差。在交通系统中,一旦受到比较严重的影响时,交通流数据极大可能存在大范围的丢失。因此,应做出更大的努力来提高模型的稳定性,以满足在数据存在系统丢失的情况。此外,本研究仅考虑随机和连续丢失数据的情况,而没有考虑在特殊情况下(如事故情况和天气影响)丢失数据的情况。在这种情况下,流量检测仪器可能会完全无法检测与记录数据,流量数据将存在系统丢失的情况。数据系统的缺失意味着一定时间内数据会完全丢失。系统缺失的数据补齐是未来需要进一步突破的挑战。在未来,可以考虑多个检测器之间的时空相关性以提高插补精度,进一步考虑道路网的交通流数据之间的关系,系统地补齐交通流丢失数据,为交通道路网系统的研究提供一定的数据支持,最终可为智能交通的发展奠定数据基础。
1.3 粗糙支持向量聚类




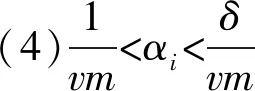
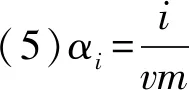

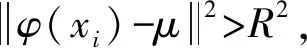
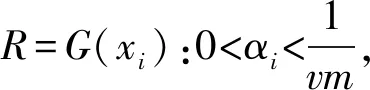
2 模糊神经网络和遗传算法数据补齐模型
2.1 模糊推理系统

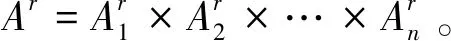

2.2 模糊神经网络

2.3 模糊神经网络和遗传算法数据补齐

3 交通流数据修复模型
4 实例分析
4.1 数据准备

4.2 粗糙支持向量聚类分类结果

4.3 模糊神经网络和遗传算法数据补齐结果
5 结论

