不确定条件下任务风险分析的贝叶斯网络方法

田文杰,徐吉辉,郝旭祥

(空军工程大学装备管理与无人机工程学院，西安 710051)

1 引言

随着复杂装备不断装配部队，以此为支撑遂行的作战任务样式也在发生巨大变化。目前作战任务已经实现了从单一到多元、从简单到复杂的转变，呈现出不确定性、模糊性、涌现性、集成性和多态性等特点。任务系统的复杂结构、高精度技术要求、多要素耦合性等因素已经引发了许多不确定性问题，所以需要开展风险分析保证任务的顺利实施。目前常用的风险分析方法有：贝叶斯网络[1-2]、Bow-tie模型[3]、STAMP模型[4-5]、Petri网[6]、FMEA[7]和HAZOP[8]等。贝叶斯网络作为典型的不确定性知识表达和推理模型，具有双向推理机制，适用于致因分析，已广泛应用于风险评估[9-10]、故障诊断[11-12]、可靠性分析[13]等领域。

贝叶斯网络风险分析方法通常使用精确值进行定量计算，但数据的随机不确定性及专家的认知不确定性往往会导致风险分析结果的不准确。DS证据理论[14-15]和模糊集理论[16-17]是解决不确定问题的主要方法，但因为DS证据理论的悖论问题无法有效解决，所以模糊集理论被广泛应用于解决不确定性问题，并与贝叶斯网络相结合进行风险分析。

由于贝叶斯网络推断过程计算量复杂，Netica、Hugin和Genie等软件被开发进行贝叶斯网络的计算。文献[18]引入模糊理论确定各节点状态的发生概率，使用Netica软件进行贝叶斯网络推理；文献[19]将模糊数学和贝叶斯网络相结合，使用Genie对航空安全事故进行风险分析。文献[20]针对复杂装备的不确定特性，提出基于故障树的模糊贝叶斯故障诊断推理模型，使用Genie找出关键故障要素，解决了由于数据缺失和专家打分导致的结果不精确问题；文献[21-22]使用模糊集理论和置信度理论与贝叶斯网络相结合，在不确定问题的处理上取得了良好的效果，但并未应用于工程实践问题，对于节点重要程度的判别标准也比较单一。

综上所述，目前贝叶斯网络的研究仍存在以下问题：① 对模糊数进行去模糊化处理会导致不确定信息在一定程度上的缺失；② 叶节点的条件概率仅使用简单的逻辑关系“与”和“或”进行表示，计算结果可信度不高；③ 用模糊理论进行不确定性描述，虽然解决了数据缺失导致的先验概率及条件概率难度量的问题，但受专家主观影响较大；④ 对于根节点重要程度的确定标准较为单一，以此作为风险预防的判断依据不合理。

针对上述问题，将模糊理论和置信度应用到贝叶斯网络中，提出一种模糊置信贝叶斯网络模型并开展任务风险分析，并以重装空投任务为例进行验证。首先，在专家确定模糊概率的基础上引入置信区间，对模糊概率进行区间描述，提高结果的置信水平；其次，从后验概率变化率及变化度等2个方面进行灵敏度分析，确定根节点的重要程度；最后，与其他模糊贝叶斯网络方法进行对比分析，以验证本文方法的有效性和先进性。

2 模糊置信贝叶斯网络方法

2.1 模糊置信贝叶斯网络构建方法

贝叶斯网络(bayesian network，BN)是通过有向无环图描述随机变量集及其条件依赖性的概率图模型，可以表示为:

(1)

(2)

模糊数学主要依靠隶属度函数进行不确定问题的研究，本文采用三角模糊数描述风险节点发生的可能性程度。

基于传统贝叶斯网络和模糊理论，本文提出模糊置信贝叶斯网络的任务风险分析流程，如图1所示。

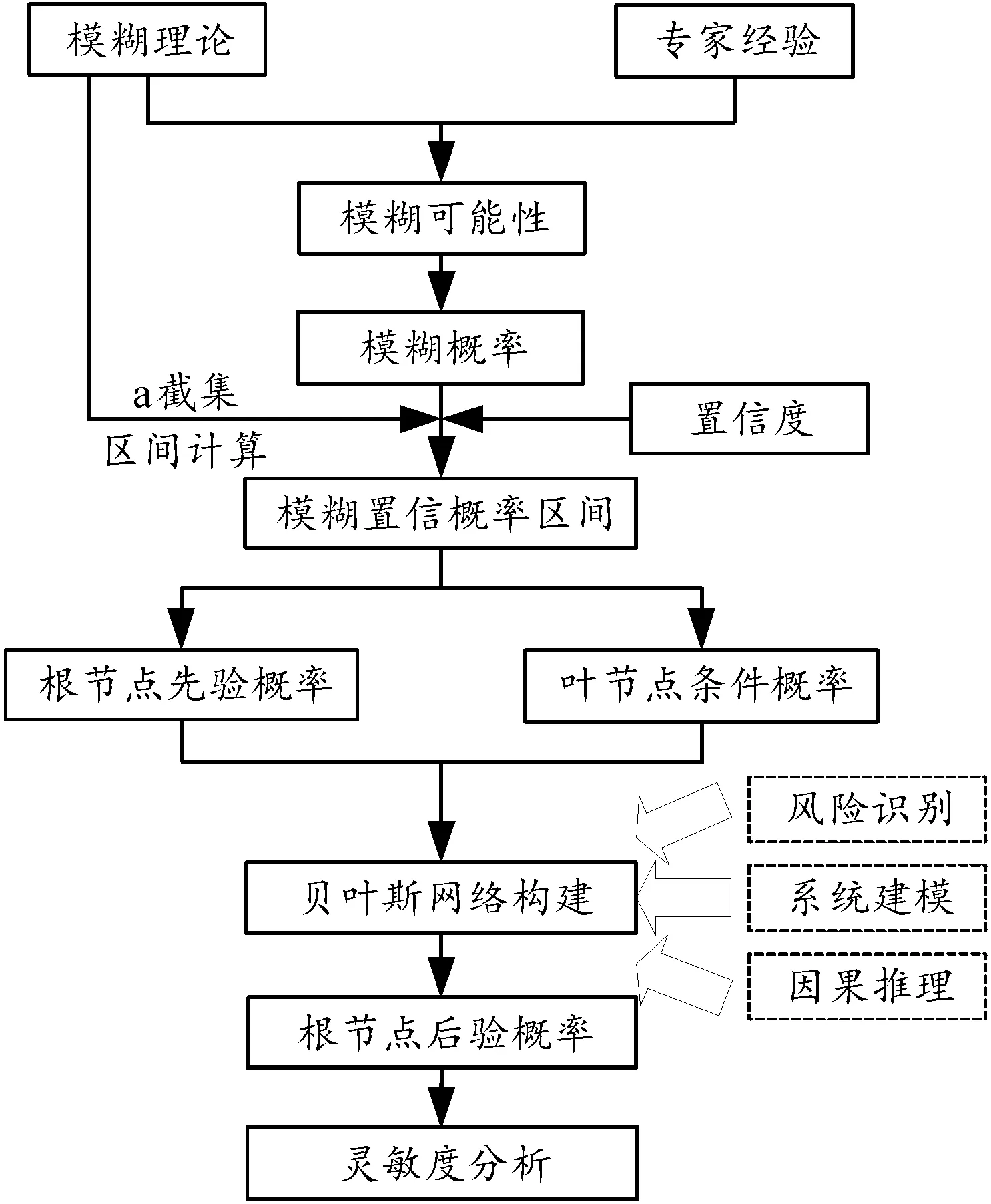
图1 任务风险分析流程

2.2 模糊置信贝叶斯网络构建方法详细步骤

在工程实践中，由于系统中存在的随机不确定性和认知不确定性，人们很难准确把握所有风险节点的发生概率。因此，基于专家经验和模糊理论，提出模糊置信贝叶斯网络进行风险分析研究。

2.2.1模糊概率计算

由于专家经验没有一定的理论支撑，通过模糊理论和专家经验相结合，能够确定模糊可能性(fuzzy prossibility,FPs)进行模糊概率(fuzzy probability,FPr)的计算。

假设xi为风险节点，其发生的可能性分为极不可能(NVL)、不可能(U)、可能(L)、非常可能(VL)、特别可能(EL)等5个等级，用三角模糊数表示，如图2所示。

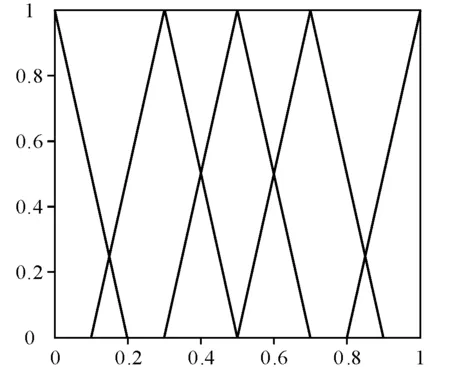
图2 隶属度函数

根据文献[23]，第i个风险节点的模糊可能性可以表示为：

(3)

式(3)中：ωj表示第j个专家的权重值；aij表示专家j对风险节点i的语言描述值。

第i个风险节点的模糊概率值可以表示为：

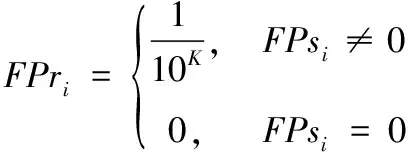
(4)

(5)

2.2.2模糊置信概率区间的确定

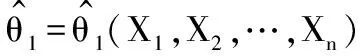
(6)

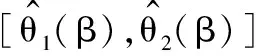
(7)

则p的置信区间为：

(8)

则p的置信度为1-β的置信区间为：

(9)

则三角模糊概率p的模糊置信概率区间可以表示为：

同理，可以根据上述方法确定风险节点的模糊置信条件概率区间。

由于α∈(0,1]，可以表示所有(1-α)100%的置信区间。因此，本文提出的模糊置信概率区间比点估计和置信区间能够更好地描述不确定信息。

2.2.3模糊置信后验概率区间

由于复杂系统中各要素之间相互耦合，不确定性特征明显，对风险概率求解结果的准确性影响较大，难以使用确定值计算风险节点的后验概率值。因此，本文根据各风险节点的模糊置信概率区间及模糊置信条件概率区间进行区间计算，区间计算原理如下：

给定模糊数A(α)=[a1,a2]，B(α)=[b1,b2]，则：

A(α)+B(α)=[a1+b1,a2+b2]

(10)

A(α)-B(α)=[a1-b2,a2-b1]

(11)

A(α)·B(α)=[a1,b1]·[a2,b2]=

[min(a1·a2,a1·b2,a2·b1,a2·b2),

max(a1·a2,a1·b2,a2·b1,a2·b2)]

(12)

A(α)/B(α)=[a1,b1]/[a2,b2]=[a1,b1]·[1/b2,1/a2]

(13)

(14)

针对A、B节点获取信息是否精确的情况，给出模糊置信后验概率区间的4种形式，有：

1)A、B节点获取信息精确，则：

(15)

2)A节点获取信息精确，B节点获取信息模糊，则：

(16)

3)A节点获取信息模糊，B节点获取信息精确，则：

(17)

4)A、B节点获取信息模糊，则：

(18)

2.2.4灵敏度分析

通过对复杂不确定系统进行风险识别、系统建模、因果推理，构建模糊置信贝叶斯网络。模糊置信贝叶斯网络不仅能够量化各节点风险发生的可能性，还能表征各节点之间的逻辑关系，有效进行风险分析。基于贝叶斯网络的双向推理功能，还能对节点进行灵敏度分析，确定各节点的重要程度，提供相应的防范措施。

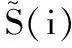
通过计算可以求得第i个节点的概率变化率S(i)为：

(19)

(20)

3 重装空投任务风险分析

重装空投任务是一项大型的复杂不确定系统，具有多人员、多系统协调配合、环境依赖性强、潜在风险隐蔽性高等特点。掌握重装空投技术对于实现我军快速机动、把握战场主动、提高我方火力优势具有重要作用。因此，本文以重装空投任务为研究对象，基于贝叶斯网络开展风险分析，并与文献[23]中的方法进行对比，验证本文所提方法的有效性。

3.1 任务描述与系统建模

重装空投任务剖面如图3所示。重装空投任务剖面主要分为飞行前准备(装载装备物资、飞行前检查)、起飞到达指定空域、装备货盘出舱、装备货盘空降、着陆缓冲、返航等6个阶段，各阶段的具体描述如下。

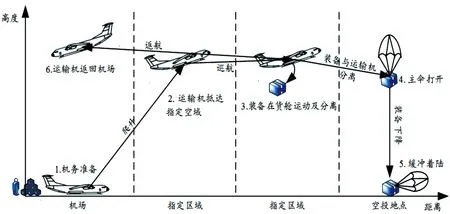
图3 重装空投任务剖面

1)飞行前准备：将要进行空投的装备、物资与降落伞系统可靠系留在空投货台上，使用机载电动吊车将货盘移动到货舱指定位置进行辅助系留，保证货盘不移动。随后安装牵引伞系统，使牵引绳与货台锁紧密连接，设置应急系留链和牵引伞的伞绳切割器，以应对紧急情况的发生，最后关闭登机门和货舱门。

2)起飞到达指定空域：飞行员正常巡航，驾驶飞机到达指定空域，针对具体情况保持货盘能正常出舱所需的俯仰角。同时，对货舱进行释压，解除货盘的辅助系留设置，在空投人员对货舱的状态检查完毕后，打开货舱门和登机门。

3)装备货盘出舱：空投人员向飞行员报告，得到许可后按下“投放”按钮，牵引伞在货舱尾部的牵引伞包挂钩上脱离、抛出，牵引伞充气张满，拉断定力绳，货盘在牵引伞作用下牵引货盘沿导轨出舱。在货盘出舱后，空投人员向飞行员汇报，得到许可指令关闭货舱门及登机门。

4)装备物资空降：货盘离机瞬间，牵引锁打开，牵引绳被拉直并提起引导伞，在引导伞张满后提起主伞包，并顺序打开减速伞和主伞，保持主伞及减速伞处于稳定的充气状态，同时主伞上的收口绳受力，使主伞保持“灯泡”状，在减速伞张满后，收口绳被切割器切断，主伞经2次充气张满，保证货盘系统稳定下降。

5)着陆缓冲：在货盘着陆后，缓冲系统依靠自重充气，实现对装备物资的缓冲。与此同时，着陆脱离锁工作，装备物资和主伞脱离，防止主伞系统对装备进行拖拽。定向防翻系统对货盘进行调整，达到抗风防翻的目的。

6)返航：在装备货盘出舱后，飞行员驾驶飞机安全返航。

本文中主要对单机单任务的牵引式重装空投开展研究。假设空投时运输机距离地面一定高度，投送装有武器弹药的集装箱，空投区域天气状况良好，地面威胁程度低，从人-机-环3个角度进行风险识别，具体节点描述见表1，建立重装空投因果推理图，如图4所示。

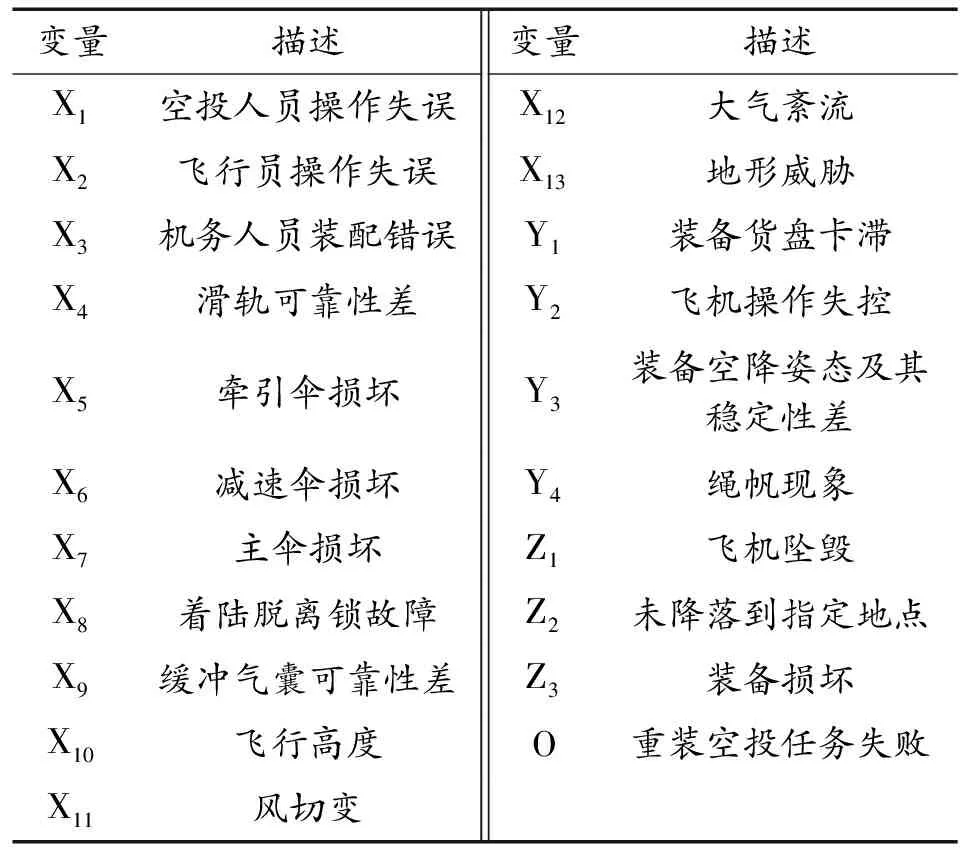
表1 节点描述

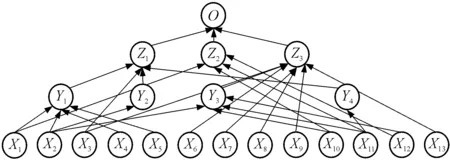
图4 重装空投任务因果推理图

由于客观原因，许多节点的先验概率无法确定，因此邀请5名重装空投领域的专家进行预测，本文以节点X1为例求解模糊置信概率区间。

1)计算专家权重。本文根据专家研究重装空投理论的时间、受教育程度、重装空投实操经验等方面，采用层次分析法[24]求解得5名专家权重ω=(0.16,0.23,0.28,0.14,0.19)。

2)计算模糊置信概率区间。通过专家打分，可得风险节点X1的可能性为a1=(0.3,0.16,0.2,0.1,0.15)，由式(3)、式(4)、式(5)可得风险节点的模糊可能性FPs1=0.183 3、模糊概率FPr1=0.016 4。本文选取α=0.01，求得节点X1发生的模糊置信概率区间为[0.006 4,0.026 4]。

当FPr≤0.01时，设置α=0.01，此时FPr-α≤0，不符合常理，则设置模糊置信条件概率区间左边界为0。同理，当FPr+α≥1时，设置模糊置信条件概率区间右边界为1。通过计算，可得其他各风险节点发生的模糊置信概率区间，如表2所示。

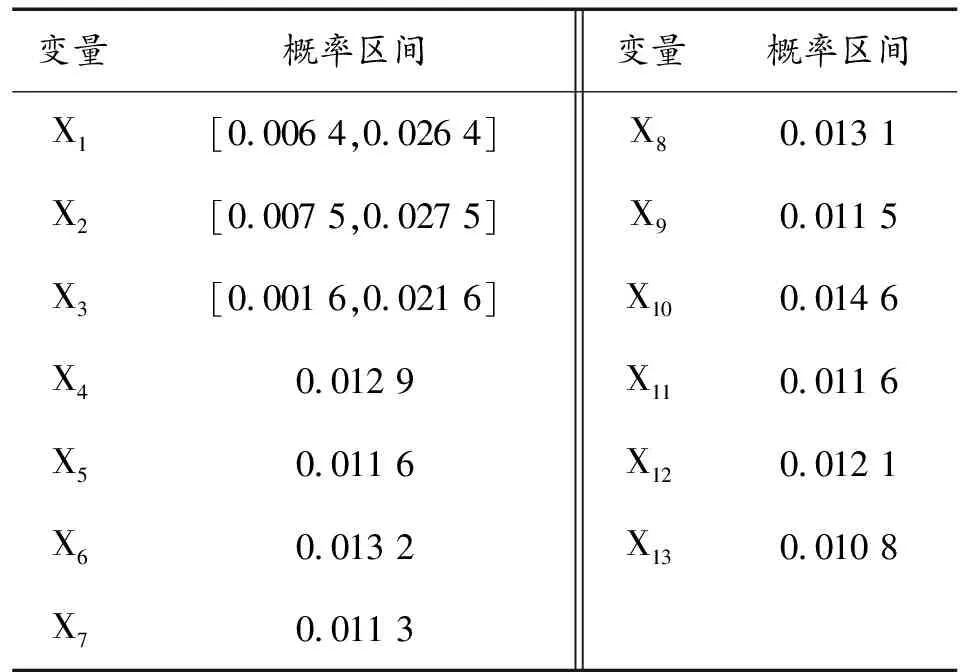
表2 根节点模糊置信概率

3)计算模糊置信条件概率区间。以叶节点Y1为例，具体计算过程为：由图4可知，Y1节点有4个根节点X1、X2、X4、X5，且这4个基本事件相互独立，通过计算可得节点Y1模糊置信条件概率区间如表3所示，其中“1”代表发生，“0”代表不发生。

表3 Y1条件概率

同理可求得其他节点模糊置信条件概率区间,通过计算得到各根节点的后验概率区间如表4所示。

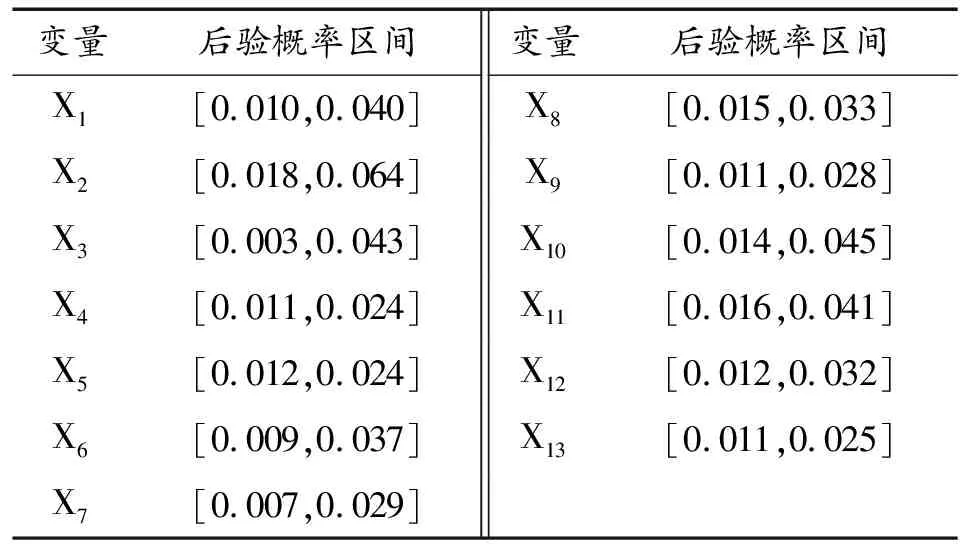
表4 根节点后验概率

3.2 风险节点灵敏度分析

本文中假设当重装空投任务失败时，将根节点的先验概率减少10%进行灵敏度分析，可得根节点的变化率及变化度，并根据重要程度进行排序，如图5所示。

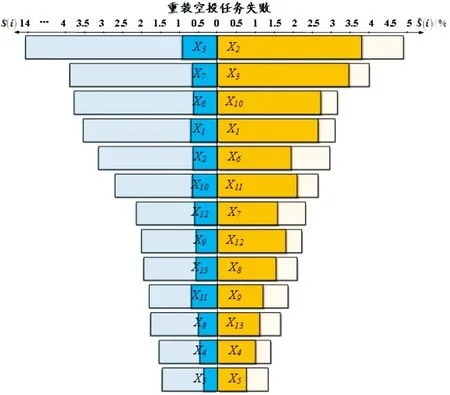
图5 灵敏度分析龙卷风图

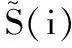
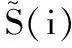
综上可得，加强对于飞行员、空投人员以及机务人员的专业训练是保证重装空投任务成功的决定因素。同时，运输机上各系统、装备本身的可靠性及所处的环境条件也是任务成功的重要因素，因此在任务实施前要注意对运输机各系统的检查及对环境的侦测。

3.3 对比分析

为验证本文所提方法的有效性及先进性，本文主要与文献[23]中的方法进行对比分析，通过软件Genie构造贝叶斯网络，如图6所示，各根节点先验概率调整10%的后验概率对比如表5所示。

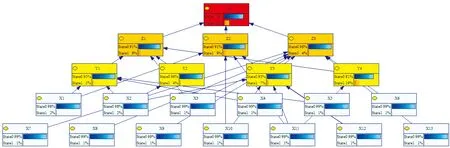
图6 重装空投贝叶斯网络

由表5可得，文献[23]中求得的后验概率均在本文中所提方法的概率区间之内，说明本文方法在不确定条件下进行任务风险分析是有效的。

表5 根节点后验概率对比

本文方法的先进之处主要有以下几点：首先，针对传统贝叶斯网络节点概率难以精确度量的问题，引入模糊理论确定模糊概率；其次，在仅使用专家意见确定模糊概率的基础上，本文使用置信度确定模糊置信区间，能够通过调节置信度大小，以更大范围量化不确定特征，对于不确定性问题处理具有更高的适应能力；接着，由专家意见得到模糊概率，使用精确值表示不符合客观实际，使用区间进行范围表示有更高的容错特性；最后，基于模糊理论和置信度描述不确定信息，使本文方法有一定的理论支撑，对于工程实践具有应用意义。

4 结论

将模糊理论和置信度引入贝叶斯网络中，提出模糊置信贝叶斯网络方法，能够在不确定条件下有效开展任务风险分析。主要结论如下：

1)使用区间表征各节点的状态，更有利描述现实任务条件下，风险传导复杂多样的逻辑关系，提高贝叶斯网络在不确定性条件下进行风险分析的能力；

2)克服了数据缺失、系统复杂、专家评估主观性强等因素导致的不确定性对任务风险分析结果的影响；

3)本文通过某次重装空投任务的风险分析实例，介绍了所提方法在任务风险分析、灵敏度分析等方面的应用可行性，在不确定条件下对复杂任务系统进行风险分析提供参考依据。