多值置信的格值闭包算子及Galois联络*
方进明,张 虎,褚晓清
(中国海洋大学数学科学学院,山东 青岛266100)
0 引言与预备
闭包算子及其闭包系统是经典数学中诸多分支的研究对象,且可以描述计算机科学中经常出现的Galois联络现象。从1980年代起,以Gerla及其合作者为代表的诸多学者在模糊集理论的框架下,对模糊闭包算子及其闭包系统进行了广泛研究[1-3]。
受多值逻辑(或模糊逻辑)的影响,值格上逻辑结构的介入成为格值闭包算子及其闭包系统研究的方向,如,2001年,Bělohlávek在文献[4-5]中用完备剩余格上的逻辑结构作为推理模型提出了一类所谓LK-闭包算子及LK-闭包系统的概念,其中此处的K是指定格L上的经典序滤子(或滤子),借用序滤子这一工具,Bělohlávek亦在文献[5]中对模糊Galois联络现象进行了研究。又如,取K为指定格L,张德学在文献[6]中引入了与他的强L-拓扑协调的强L-闭包算子的概念;方进明在文献[7]中,在完备剩余格的环境下,提出了多值闭包系统的概念,并用范畴论方法界定了多值闭包系统与多值闭包算子的规律性联系;姚卫在文献[8]中提出了更一般的模糊偏序集上的格值闭包算子理论。
纵观上述研究工作,本文发现格值闭包算子的引入及其相关推理的多值置信化应该成为新的研究方向。应该说Bělohlávek在文献[4]中引入的经典序滤子(或滤子)已经给了有益的提示。遗憾的是由于用来描述概念与推理的多值置信化的序滤子(或滤子)是背景格的经典子集,这与多值逻辑结构介入的出发点相悖,也导致概念和推理的多值置信化难以实现。
基于上述分析,本文提出多值置信滤子的概念,并把其作为闭包算子及其相关概念多值置信化的工具。然后提出基于多值置信滤子的K-置信闭包算子的概念,并给出等价刻画。事实上,此类闭包算子与相关置信闭包系统仍然具有相互确定性。最后,本文提出了多值置信意义下的Galois联络现象及等价条件,结果表明多值置信滤子可以描述Galois联络现象。
通篇全文,L均表示完备剩余格,L中的最大元记为1,最小元记为0。下面2个引理在后续内容中会常用到,证明参见文献[4-5,7,9]。



1 多值置信滤子与多值置信闭包算子
考虑到与经典置信滤子的不同,本文首先提出多值置信滤子的概念,作为闭包算子及其相关推理的工具。定义1 若映射K∶L→L满足如下性质:对任意a,b
∈L,(K1)K(1)=1;(K2)a≤K(a);(K3)K(a)k(B)≤K(ab);(K4)当a≤b时,有K(a)≤K(b)成立;则称K是L上的多值置信滤子。
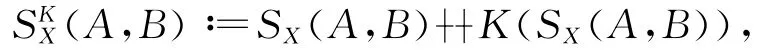
事实上,它仍是一种L-包含关系,称为K-置信L-包含关系,也满足引理2中的(6)~(10)。本文下文出现的“K”均指任意指定的完备剩余格L上的一个多值置信滤子,行文中不再特殊说明。在此背景下,我们可以引入一类新的闭包算子—K-置信闭包算子。



因此,C=Cφ(C)成立。至此,充分性证毕。
2 多值置信Galois联络
上一节介绍多值置信滤子可以作为闭包算子多值置信化的工具,本节作者探究用此工具描述多值置信意义下的Galois联络现象,并进一步证明这类Galois联络的等价刻画条件。
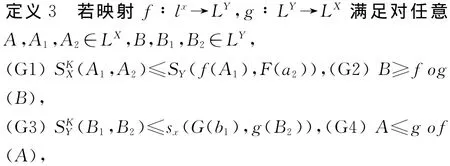


3 结语
本文通过引入多值置信滤子这一基本工具,解决了格值闭包算子和格值Galois联络的多值置信化问题,从而有效地界定了置信闭包算子和置信Galois联络的概念。本文进一步证明的置信闭包算子的刻画定理使得从理论上认清置信闭包算子的本质,即其与置信闭包系统具有相互确定性。此外,置信Galois联络的引入及其刻画条件的给出进一步回答了多值置信滤子在解决传统Galois联络现象的置信化问题中的重要作用。
[1] Biacino L,Gerla G.Closure system and L-subalgebras[J].Inform Sci,1984,33:181-195.
[2] Biacino L,Gerla G.An extension principle for closure operators[J].J Math Anal Appl,1996,198:1-24.
[3] Gerla G.Graded consequence relations and fuzzy closure operators[J].J Appl Non-Classical Logics,1996,6:369-379.
[4] Bělohlávek R.Fuzzy Closure Operators[J].J Math Anal Appl,2001,2622001:473-489.
[5] Bělohlávek R.Fuzzy Galois Connections[J].Math Logic Quart,1999,45(4):497-504.
[6] Zhang D.An enriched category approach to many valued topology[J].Fuzzy Sets and Systems,2007,158:349-366.
[7] Fang Jinming,Yue Yueli.L-fuzzy closure systems [J].Fuzzy Sets and Syetems,2010,1612010:1242-1252.
[8] Yao Wei,Lu Lingxia.Fuzzy Galois connections on fuzzy poset[J].Math Logic Quart,2009,55(1):105-112.
[9] Goguen J A.L-fuzzy sets[J].J Math Anal Appl,1967,18:145-174.

