一种求解旅行商问题的改进蚁群算法＊

王沛栋，唐功友，杨熙鑫，李 扬

（1.中国海洋大学信息科学与工程学院，山东 青岛266100；2.青岛市产品质量监督检验所，山东 青岛266101）

旅 行 商 问 题 （Traveling Salesman Problems，TSPs）是组合优化领域中一个重要的问题之一，也是现实中许多复杂问题的集中概括和简化形式，而且由于TSPs问题的典型性，目前它已成为各种启发式搜索以及优化算法的参照标准。TSPs的任务是在已知多个城市位置的条件下，从某个城市出发，依次遍历所有城市，再返回到出发城市，为销售员设计遍历路线，使总路径长度最小或用时最少。TSPs属于NP－hard问题，采用常规方法很难得到问题的最优解。

目前求解TSPs问题有许多方法，大体可以分为2类算法，即精确算法和启发式算法。精确算法主要指动态规划和分支限界法［1］等；启发式算法包括：遗传算法［2－3］、蚁群算法［4－11］等。在蚁群算法中，文献［4］提出蚂蚁系统（Ant System ，AS）算法，算法通过随机方式进行路径选择，而且每次迭代结束后对信息素进行更新；文献［5］提出蚂蚁群系统（Ant Colony System ，ACS）算法，算法使用最优选择和随机选择结合的路径选择方式，信息素更新采用局部更新和全局更新，提高了算法的全局的收敛能力；文献［6］提出最大最小蚂蚁系统（Max－Min Ant System ，AS）算法，算法在 AS算法基础上，通过限制信息素的大小范围，使算法不致于陷入停滞状态，性能较AS有较大的提高；文献［7］提出一种基于信息素扩散的蚁群算法（Pheromone Diffusion Ant colony Optimization，PDACO），算法通过建立信息素扩散模型，使相距较近的蚂蚁之间能更好地进行协作；文献［8］提出一种基于遗传算法和蚂蚁算法的融合算法，它采用遗传算法生成信息素分布，再利用蚂蚁算法进行求解；文献［9］提出一种带有变异策略和信息素动态更新的蚁群算法，变异策略增加了搜索的多样性，信息素动态更新方式加快了最优解的收敛速度；文献［10］提出一种带有变异过程和局部搜索的蚁群算法求解TSPs问题；文献［11］提出一种基于信息素增量和路径散播模型的蚂蚁群算法（ACO algorithm based on new pheromone increment and path diffusion models，PIPDMACO），它建立了信息素增量模型和信息素散播模型，并且使用复杂度更低的变异策略对每次的迭代结果进行优化。

本文在蚁群系统算法的基础上提出一种求解TSPs问题的改进算法。其中，在信息素更新过程，利用信息素局部更新和全局动态更新结合的方法，使得局部最优路径上的信息素值动态地调配，避免了算法陷入停滞状态；在局部搜索过程中，仅对部分走出更优路径的售货员使用2－opt方法，加快了最优解的收敛速度。

1 问题描述及数学模型

TSPs问题是由1名售货员对多个城市进行配送服务的问题。在已知城市位置的前提下，设计售货员配送路线，每个城市只能被访问1次，使运输成本最小化，即总代价最小（行走总距离最短或耗费时间最少）。用数学模型表达，根据TSPs问题中的城市分布，可以建立1个无向图G（V，A），包括节点集

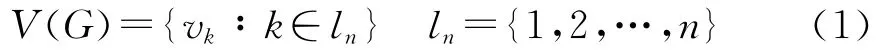
和边集

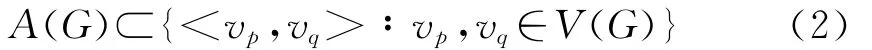
其中：n为城市的数量；vk表示城市k＜vp，vq＞表示城市p与城市q之间的路径；设dij为城市i到城市j的距离，

TSPs问题的目标是为售货员寻找最优的遍历路线，使运输成本J达到最小值，

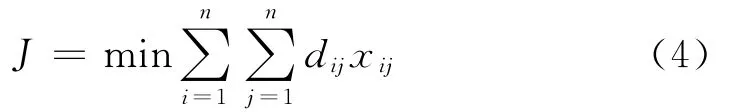
且应满足以下约束条件：

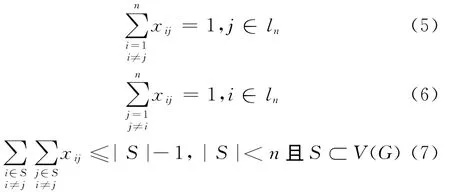
式（5）表示售货员仅有1次机会到达城市j；式（6）表示售货员仅有1次机会离开城市i，式（5）与式（6）共同保证了售货员对每个城市只能访问1次；式（7）为子回路限制条件，保证在规划的路径中没有其它的回路。

2 算法设计

使用蚁群系统算法求解TSPs问题时，一般将蚂蚁看作售货员，信息素τij表示售货员处于城市i时，城市j对售货员的吸引程度。在每次迭代之前，售货员会随机地选择1个初始城市，然后按照路径选择规则来构建路径，售货员每选择1个城市，就对所走过的路径进行信息素局部更新。当所有售货员的路径构建完毕时，就对每条路径使用2－opt方法进行局部搜索，选取当前最优路径进行信息素全局更新，从而完成1次迭代。经过数次迭代后，算法可以得到一个优化解。

根据以上算法过程的简述可知，算法可以分为3个部分：路径选择、信息素更新和局部搜索。本节将分析蚁群算法求解TSPs问题中信息素更新和局部搜索中的局限性，并提出相应的策略对其进行改进，最后将总结改进算法的步骤。

2.1 路径选择方式

路径选择方式采用蚁群系统路径选择模型［5］。假设售货员k在t时刻处于城市i时，下一步可能选择的城市为j，其路径选择公式为：

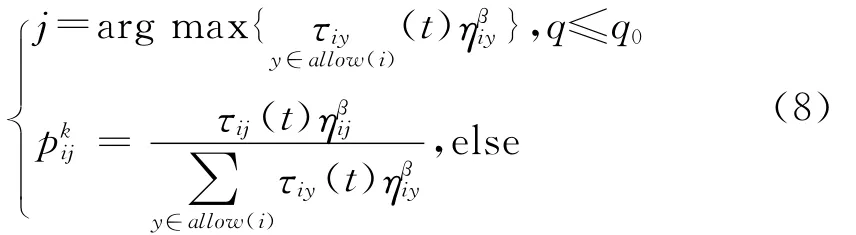
其中：τij（t）表示t时刻，路径（i，j）上的信息素值；启发式信息ηij＝1／dij，用来引导售货员向路径更短的城市移动；allow（i）表示售货员处于城市i时，候选城市的集合；β为权值系数，用来决定启发式信息的重要程度；q表示1个［0，1）的随机值；q0表示设定的阈值（0.8～0.95）。式（8）能够使售货员以较大的概率q0向信息素和启发式信息乘积最大的城市移动，而以较小的概率（1－q0）使用随机比例原则选择城市。这种方式既保证了售货员选择的方向性，又增加了售货员搜索的多样性。

2.2 信息素更新方式

目前，求解TSPs问题的蚁群算法使用的信息素更新方式包括蚂蚁系统信息素的更新方式［4，6，8］和蚁群系统信息素的更新方式［5，7，9－10］等。然而这些方法都普遍存在同样的问题，在迭代过程中，当新的最优路径还未出现时，当前最优路径上的信息素在更新策略的作用下会不断增强，可能会产生2种消极的结果：首先，当前最优路径上信息素可能会因过度加强而导致算法停滞；其次，当新的最优路径出现时，其路径上的信息素强度可能会远低于原最优路径上的信息素强度，有时经过数次迭代这种情况依然没有得到缓解。总之，目前的更新方式使当前最优路径的变化不能迅速地表现在路径的信息素分布上，从而降低了搜索的效率。

针对以上信息素更新方式局限性的分析，本文提出一种局部更新和全局动态更新相结合的信息素的更新方式。

（1）局部更新

在路径构建过程中，售货员每经过一条边（i，j）都会使用下式来更新该边上的信息素。

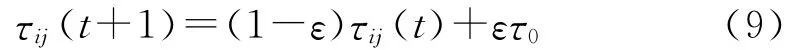
其中：ε为局部更新的蒸发率；τ0为信息素的初始值。信息素局部更新的作用在于，售货员每经过一条边（i，j），该边的信息素将会减少，从而降低其它售货员选中该边的概率，这将增加售货员探索其它未使用过边的机会。

（2）全局动态更新

当1次迭代结束后，将当前最优路径使用下式进行信息素全局更新。

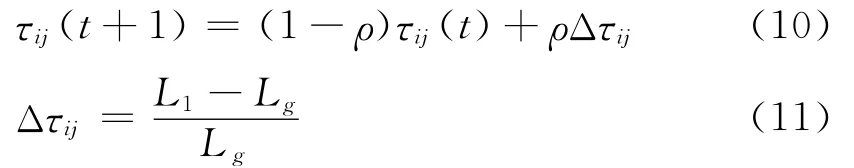
其中：ρ为全局更新的蒸发率；Δτij为全局更新信息素增量；L1为当前迭代最优路径长度；Lg为当前最优路径长度。更新当前最优路径上的信息素在于对最优路径的继续开发，将当前最优路径对信息素的反馈保留到下一次的迭代中去，直到有更优的路径取代为止。

式（10）和（11）能够根据售货员所构建路径的情况动态地调整当前最优路径上的信息素。在迭代过程中，当一条更优路径出现后，L1和Lg的差值开始可能会比较大，这说明当前最优路径与大多数售货员走出的路径存在较大的差异，走出当前最优路径的售货员所占比例很小。此时，式（11）能够加大当前最优路径上信息素的强度，以吸引更多的售货员。而随着迭代的进行，当前最优路径上的信息素不断增强，更多的售货员会聚集到这条路径上来，L1和Lg的差值会逐渐减小，此时，式 （11）能够相应地减小信息素增量，直至减小到0。当式 （11）减小到0时，当前最优路径上只进行信息素蒸发，对信息素进行削弱。该方法能够使当前最优路径上的信息素强度更为突出，但又不会因过度加强而造成算法的停滞，使当前最优路径的变化更快地反映在信息素的分布上。

2.3 局部搜索策略

2－opt方法是求解TSP问题经常使用的一种方法。图1描述了2－opt方法对路径的搜索过程，如图1所示，A为搜索之前城市访问的路径，B为使用2－opt方法后城市访问的路径。文献［5－6，9－10］分别将其应用到迭代后的每名售货员所构建路径的路径中。使用这种方法可以提高解的质量，为下一步选取当前最优路径进行信息素全局更新做准备。但是，使用2－opt方法非常消耗时间，如果问题规模和售货员的数量比较大，这种方法会消耗大量的时间，这也是以上算法［5－6，9－10］求解时间过长的原因之一。

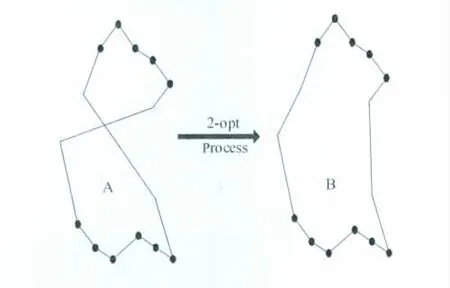
图1 局部搜索2－opt过程Fig.1 Schematic diagram of the 2－opt process

针对以上对局部搜索局限性的分析，本文局部搜索方法：

（1）在每次迭代结束后，将所有售货员所构建的路径，按照路径长度升序排列。

（2）从排列中选取路径长度最短的m／2（m为售货员的数量）条路径使用2－opt方法进行局部搜索。

使用这种方式的原因在于，作者通过实验发现，蚁群算法每次迭代后，在对每个售货员构建的路径使用2－opt方法的过程中，大部分售货员的结果对当前最优解并没有贡献，也就是说，并非所有路径使用2－opt方法都能够对当前最优解的选取有所帮助，而当前最优的结果往往来自当前迭代中更短的那些路径。这就造成了在蚁群算法求解过程中，由于对那些没有帮助的路径使用2－opt方法而消耗大量的时间。在本章改进蚁群算法中，算法在每次迭代后，仅对部分更优的路径使用2－opt方法，这种方式可以节省部分计算时间，又不会降低搜索效率。

2.4 算法步骤

根据以上改进策略的描述，总结改进算法步骤如下：

Step1参数初始化。令迭代计数器NC＝0，设置当前最优路径长度S、最大的迭代次数T、城市之间的距离dij（i，j＝1，…，n）、当前最优路径表t、启发式信息ηij（i，j＝1，2，…，n）、路径上的信息素τij（i，j＝1，2，…，n）。

Step2售货员位置初始化。初始化m名售货员的禁忌表tk（k＝1，2，…，m）、所走路径长度lk（k＝1，2，…，m）。所有的售货员随机地选择初始城市，将所选的城市添加到tk中，并更新lk的值。

Step3路径构建。每名售货员按式（8）进行路径选择，将所选的城市添加到tk中，并更新lk的值。

Step4信息素局部更新。售货员每选择一个城市，就对刚刚走过路径（i，j）根据公式（9）进行信息素局部更新。Step5 2－opt局部搜索。当所有售货员完成对全部城市的搜索，路径构建完毕时，将所有售货员的路径长度按升序排序，然后选取路径长度最小的m／2名售货员的路径进行2－opt局部搜索，并更新lk和tk。

Step6信息素全局动态更新。统计当前最优路径，将lk与S进行比较。若lk＜S，则lk替换S，t替换tk。对当前最优路径根据公式（10）和（11）进行信息素全局动态更新。

Step7迭代循环。若NC≤T，则返回Step2，开始新一次的迭代，否则算法结束，输出最优路径S和最优路径表t。

3 仿真实验

算法将从旅行商问题公共数据集中选择标准算例进行测试，使用BCB＋Matlab进行程序编写，并在CPU 为Intel Celeron 1.0G，内存512M 的计算机上运行，实验参数为：ρ＝0.1～0.2，ε＝0.1～04，β＝2～5，m＝15～30，q0＝0.7～0.95。从数据集中选择 Oliver30算例进行测试，该算例包含30个城市，算法对其计算结果见图2，从图中可以看到，算法经过3次迭代，就可以得到最优路径，其路径长度为432.74。图2（a）描述了算法对Oliver30算例最后得到的最优路径图，图2（b）描述了算法每次迭代的当前最优路径长度。

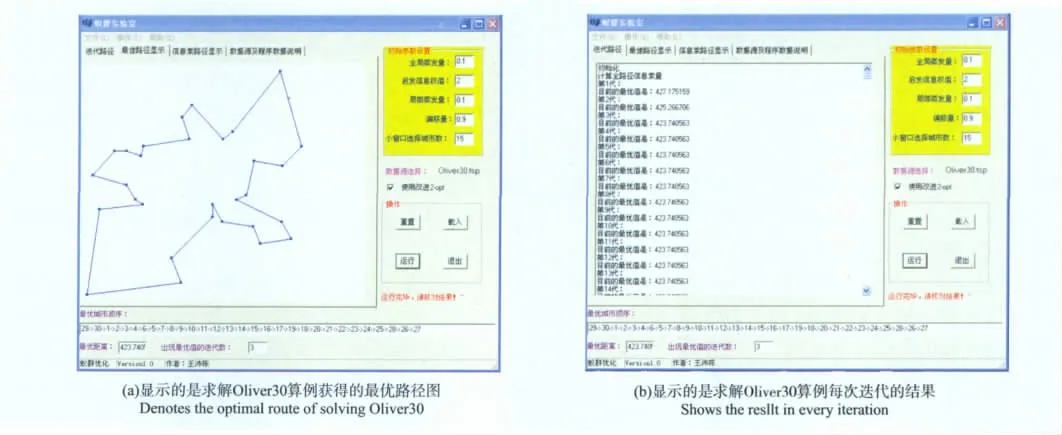
图2 Oliver30数据计算结果Fig.2Simulation result of Oliver30

从数据集中选取部分算例进行测试，每组算例运行10次，其结果如表1所示，其中，BK表示目前每组算例提供的最优参考结果。Best result表示本文算法获得的的最优结果。Num of cycles表示算法取得最优解时，使用的最少迭代次数。由表1可以看到，算法对10组算例都能够取得目前最优解，而且最优解所需的迭代次数最大为72次。

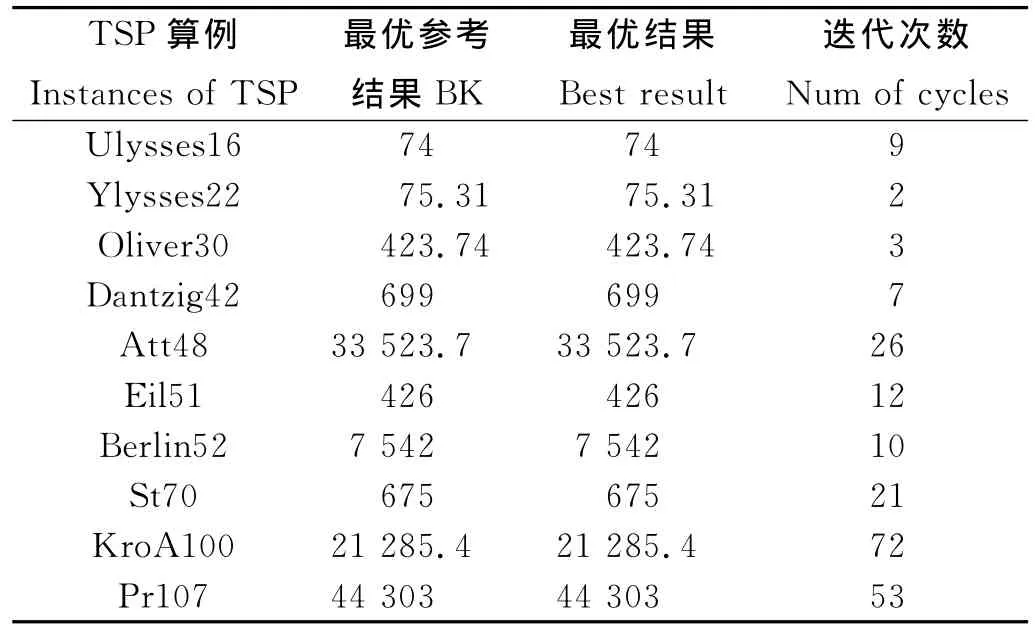
表1 本文算法计算结果Table 1 Best results for our algorithm on various instances

此外，将本文算法与其它算法进行比较，包括ACS［5］，ACS＋2－opt［11］，PDACO［7］，，PIPDMACO［11］，性能对比如表2所示，可以看到，在所有的算法中，PIPDMACO算法和本文算法对所有的算例均能够获得最优解，其余3种算法除Oliver30算例外，均未能获得算例的最优结果，而且这3种算法获得最优解所需的迭代次数较PIPDMACO算法和本文算法略大。此外，本文算法与PIPDMACO算法相比，求解Eil51and Pr107算例最优值所需的迭代次数要大，而求解其余4组算例迭代次数均略小些。本文方法不但能够增强信息素，而且在当前迭代最优路径长度与当前最优路径长度相等时会对信息素进行削弱，能够根据搜索结果动态地调配最优路径上的信息素。与其它方法相比，本文更新方式使最优路径的变化能够更迅速地反映在信息素的变化上，使售货员对最优路径更为敏感。综合以上实验结果可以看出，与其它算法相比，本文算法体现出良好的性能，并且在问题规模较大的情况下，解的质量也显示了较高的稳定性。

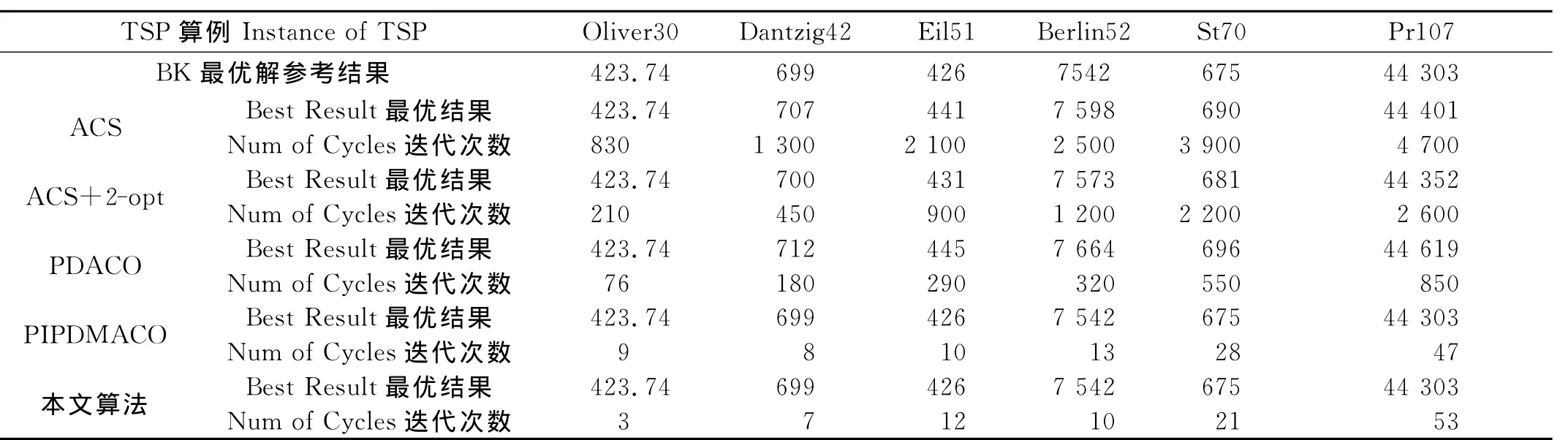
表2 算法性能对比Table 2 Comparison among the algorithm performances

4 结语

本文提出了一种基于蚁群系统算法的改进优化方法，并将其应用于求解旅行商问题。通过对标准问题的求解以及与其它方法的比较，本文算法均体现出了良好的性能。此外，该算法也可以用于其它相关类型的优化问题。

［1］ Fischetti M，Salazar J J，Toth P.A branch－and－cut algorithm for the symmetric generalized traveling salesman problem ［J］.Operations Research，1997，45：378－394.

［2］ Snyder L V，Daskin M S.A random－key genetic algorithm for the generalized traveling salesman problem ［J］.Operations Research，2006，173：38－53.

［3］ Darrell W，Doug H，Adele H.A hybrid genetic algorithm for the traveling salesman problem using generalized partition crossover［J］.Lecture Notes in Computer Science，2011，6238：566－575.

［4］ Dorigo M，Maniezzo V，Colorni A.Ant System：Optimization by a colony of cooperating agents［J］.IEEE Transaction on Systems，Man and Cybernetics Part B，1996，26（1）：29－41.

［5］ Dorigo M，Gambardella L M.Ant colony System：A cooperative learning approach for the traveling salesman problem ［J］.IEEE Transaction on Evolutionary Computation，1997，1（1）：53－66.

［6］ Stutzle T，Hoos H H.MAX－MIN ant system and local search for the traveling salesman problem ［C］.Indianapolis：Proceedings of the IEEE International Conference on Evolutionary Computation，1997：309－314.

［7］ 黄国锐，曹先彬，王煦法.基于信息素扩散的蚁群算法 ［J］.电子学报，2004，32（4）：865－868.

［8］ 丁建立，陈增强，袁著祉.遗传算法与蚂蚁算法的融合 ［J］.计算机研究与发展，2003，40（9）：1351－1356.

［9］ 朱庆保，杨志军.基于变异和动态信息素更新的蚁群优化算法［J］.软件学报，2004，15（2）：185－192.

［10］ Yang J H，Shi X H，Maurizio M，et al.An ant colony method for generalized TSP problem ［J］.Progress in Natural Science，2008，18：1417－1422.

［11］ 冀俊忠，黄振，刘椿年.一种快速求解旅行商问题的蚁群算法［J］.计算机研究与发展，2009，46（6）：968－978.