基于数据特性分析的风电机组叶片结冰辨识

董兴辉，张劲草，李 佳，高 迪，杨志凌

（1.华北电力大学 能源动力与机械工程学院，北京 102206；2.北京市城市照明管理中心，北京 100078；3.中国电力科学研究院有限公司，北京 100192）

0 引言

在一定气象条件下，风电机组叶片会出现结冰现象，既带来安全生产问题，又影响机组功率输出。针对叶片结冰条件，以及结冰对风电机组运行参数的影响，有关学者开展了比较深入的研究，按照研究内容大致归纳为数值模拟与数值仿真两种。

针对叶片雾凇、雨凇结冰，文献[1]进行了不同程度的模拟，得出雨凇对叶片表面粗糙度、叶片气动性能、风机转矩以及输出功率的影响均远大于雾凇的结果。将三维叶片简化为二维[2]，虽然可以较好地模拟雾凇覆冰，但受雨凇覆冰明显改变叶片形状，激发振动等相应复杂变化，模拟计算还有待进一步优化。采用欧拉法模拟旋转叶片覆冰过程[3]，但模型的准确性缺乏试验验证。也有基于多参考坐标系（MRF）法改进欧拉模型用于模拟旋转风机结冰[4]，还有研究覆冰对叶片不同位置、不同攻角的气动性能影响，但缺乏试验验证。文献[5]研究了叶片覆冰下桨距角的变化，得出不同功率限定值下的“桨距角-风速”曲线。文献[6]研究了叶片在不同覆冰厚度下的模态参数变化。

针对叶片结冰检测方法的研究也分为两类：气象观测检测与基于数据的分析检测。

气象观测检测是通过分析大气变化与叶片结冰的关系，间接判定叶片是否结冰；或者在机组机舱上安装专门的传感器，通过测量结冰引起的叶片物理特性变化，判断叶片是否结冰。上述方法不仅增加了机械复杂度，而且增加维护成本[7]。

基于数据分析的检测是根据专家经验知识提取数据特征，利用随机森林算法对叶片结冰进行识别[8]。但该检测方法难以全面客观地反应叶片结冰特性。文献[9]基于深度自编码网络（DNN）学习SCADA故障特征，训练几个基分类器，然后通过集成学习组合构建覆冰检测模型。也有基于叶片振动监测叶片覆冰状态[10]，根据覆冰概率与气象参数的关系，通过建立叶片覆冰概率矩阵来评估机组出力损失[11]。构建叶片结冰前后风功率曲线，取得冰冻功率折减系数[12]，对比理想功率曲线和温度偏离预测叶片结冰，基于环境温度、湿度、功率损耗建立结冰检测模型[13]。随着人工智能、大数据分析技术的发展，挖掘SCADA数据中可以表征风机叶片结冰的特征量[14]，利用粒子群算法（PSO）优化SVR回归模型，建立结冰检测模型。

1 叶片结冰的有关参量变化特性

1.1 叶片结冰的必要条件

叶片结冰与季节和气象条件密切相关。尽管不同地域存在结冰时节、结冰期长短等差异，但在结冰条件上，存在着温度、风速、液态水含量等相近特性。叶片结冰的主要影响因素如表1所示。

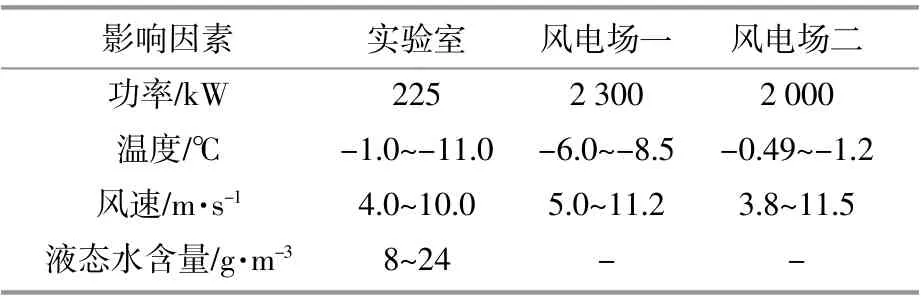
表1 叶片结冰的主要影响因素Table1 Main influencing factors of blade icing

仿真与实测数据统计表明，叶片结冰温度发生 在0～-11℃，风 速 在3.8～12m/s。

1.2 叶片结冰SCADA参数变化特性

图1为 风电 场一 在20170115T00：00-05：40时间内的SCADA系统数据（采样频率为10min，共计35个数据点）。现场运维记录显示，05：00出现机组叶片结冰。

图1 叶片结冰前后部分SCADA参数变化特性Fig.1 Variation characteristics of SCADA parameters before and after blade icing

机组在不同工况下的运行参数值如表2所示。其中，风速V、叶片转速n、功率P、桨距角 β可直接从SCADA中获取。

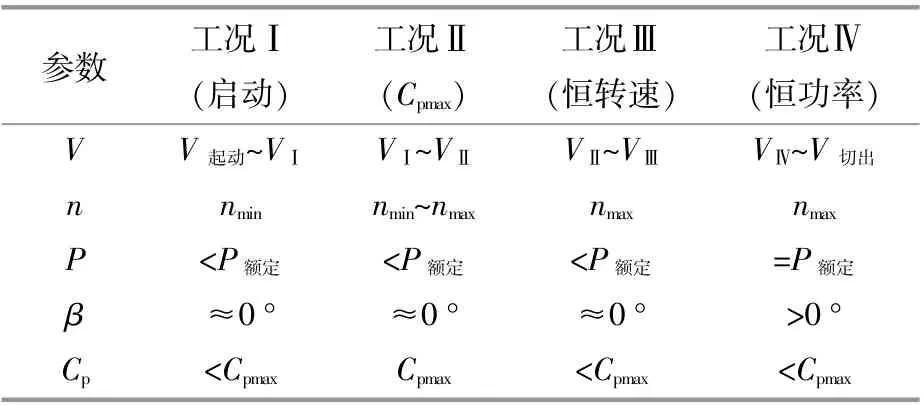
表2 不同工况下机组参数特性Table2 Parameter characteristic of the WT under different working conditions

根据风速值，对 比表2，在 序列点[1～13]时 段（图1）机组处于工况Ⅰ区，V，β，风能利用系数Cp值都处于正常状态；在序列点[13～29]时段，风速降低，机组处于Cpmax控制状态的工况Ⅱ区，V随风速减小而降低属于正常，各项参数值保持在正常范围内；在序列点[29～33]时段，风速由5.7m/s持续增大到10m/s，接近额定风速，此时机组运行于Ⅱ区-Ⅲ区边界工况区间，Cp还维持在Cpmax，β也在0°附近，V理应逐渐增大到满发状态，但从29点开始，Cp自0.43快速下降，V虽然在增大，但输出功率达不到（满发）状态Ⅲ，说明机组在转换风能方面出现异常。即从04：40时刻起叶片结冰。

运 行 在[Vmin，Vmax]，[nmin，nmax]各 工 况 区 间 上 的 机组 气 动 特 性 参 数 λmin与 λmax，Cpmin与Cpmax， 可 由 式（1），（2）计 算。

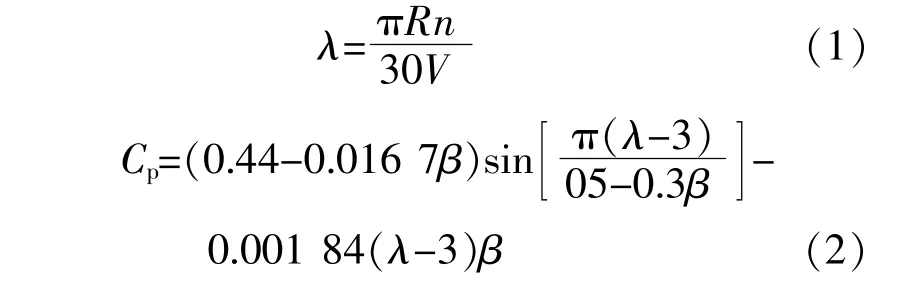
式中：λ为叶尖速比；R为叶片半径。

1.3 叶片结冰时的塔架振动特性

风力机叶片表面结冰是随机过程，呈非均匀分布，必然导致叶轮质量不平衡，机组塔架产生新的振动特性。图2为风电场二某机组在20170319 T00：00-23：59，叶片结冰前后塔架振动数据时序图（采样频率为1min，共计1440个数据点）。显然，叶 片 结 冰 前（0～450）后（450～1200）直 至 停 机（1200点之后），塔架振动特征明显不同。

图2 风电机组塔架时频振动Fig.2 WT tower time-frequency vibration

1.4 机械测风仪测值变化特性

结冰增大了测风仪转轴的摩擦力，致使其所测风速值偏小，开始出现测值误差。相对于机械式风速仪在低温环境中易受雨雪、冻雨等结冰影响，超声波风速仪则不受低温环境影响，有着更高的可靠性和准确性。因此，同一台机组上的两台测风仪在结冰前后所测风速值之差就会发生变化。设：

2 叶片结冰辨识逻辑

结冰改变叶片表面翼型，直接导致其气动性能下降，减小风能利用率，影响输出功率。叶片结冰呈无规则形状，必然引起叶轮不平衡，导致塔架产生新的振动特性。结冰期间的机械式风速仪也因结冰阻尼增大，测风精度下降。综合叶片结冰状态特性和结冰天气条件，形成叶片结冰辨识逻辑如图3所示，叶片结冰辨识流程如图4所示。

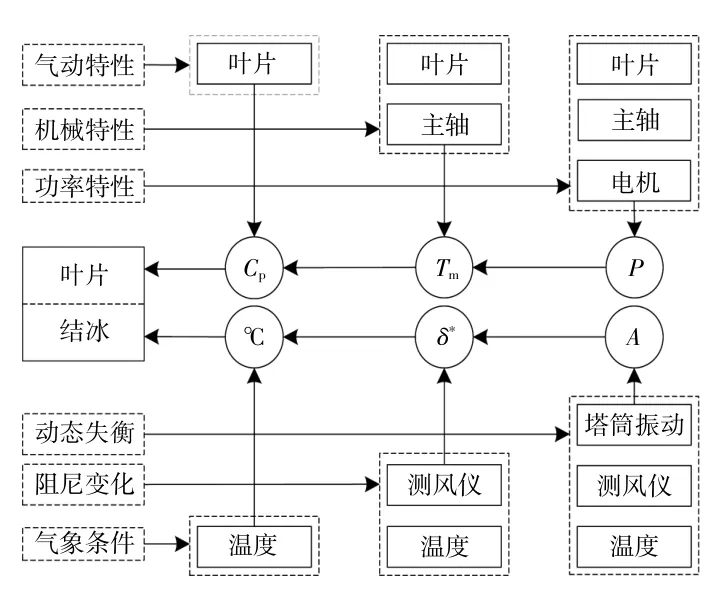
图3 叶片结冰与辨识逻辑Fig.3 Blade icing and identification logic

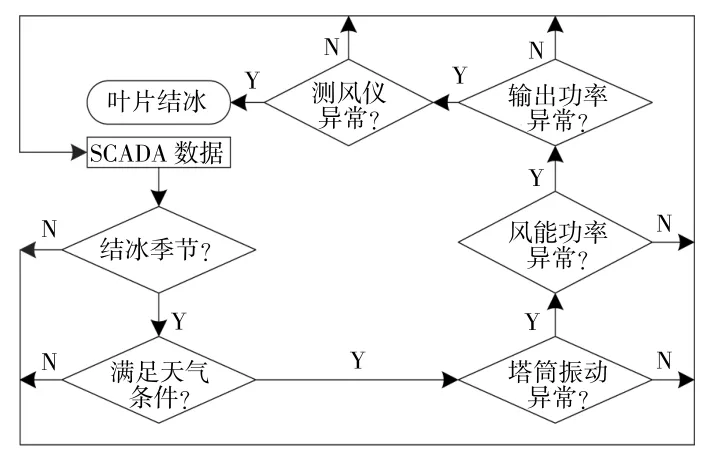
图4 叶片结冰辨识流程图Fig.4 Blade icing identification process

3 叶片结冰数值特性辨识

遴选与叶轮转换特性、振动特性、输出功率特性有关的参数，将非结冰机组历史数据划分为训练集和测试集两部分，运用支持向量机算法建立参数回归模型，计算参数历史回归值。

依据皮尔逊积矩相关系数法的相关性分析，获得机组叶片结冰状态的伴随参数。相关系数r是描述变量之间线性相关程度的量。

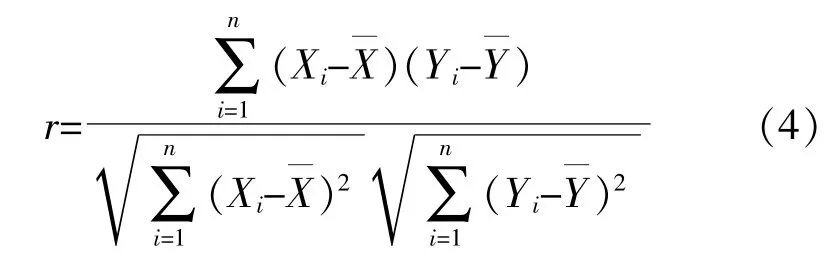
式中：Xi，Yi为变量样本；，样本平均值。

r的 取 值 为[-1，1]。当{r|-1≤r＜0}时，负 相 关；当{r|0＜r≤1}时，正相 关；当r=0时，不 相 关。r的数值越大，表明变量之间相关性越强。相关度分布如表3所示。

表3 相关度划分Table3 Divide the correlation

对于给定的输入-输出样本数据集 （xi，yi|i=1，2，…，N），其 中，xi为 第i个d维 输 入 样 本 变 量，yi为第i个输出标量，N为训练样本个数。依照优化目标函数：

式 中：w，b为 超 平 面 参 数；C为 惩 罚 系 数；ξi，为松弛变量。

对于约束条件，SVR模型的回归函数为

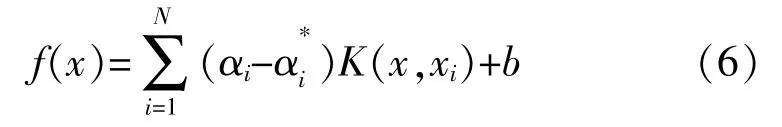
式 中：f（x）为 输 入 向 量x对 应 的 回 归 输 出；αi，为

拉格朗日乘子。

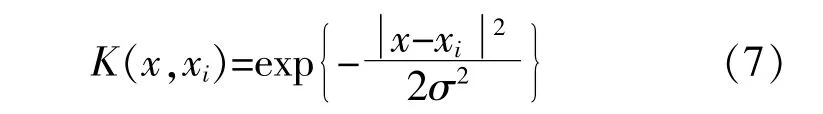
式中：σ为核宽参数。

考虑到风电机组SCADA数据具有多样本、多特征的特点，选择径向基核函数作为SVR核函数，构造支持向量机回归函数。

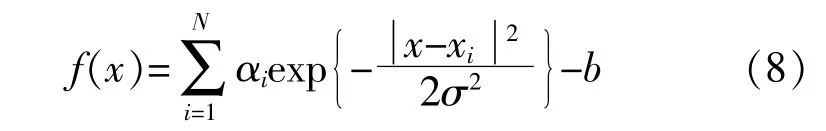
式（5）中的C和式（7）中的 σ取值，决定着SVR模型的学习能力和预测能力。为了得到具有最佳泛化性能的SVR模型，本文采用PSO算法对模型中的参数（C，σ）进行优化，从中选出最佳的C与σ。基于SVR进行参数偏离回归预测如图5所示。

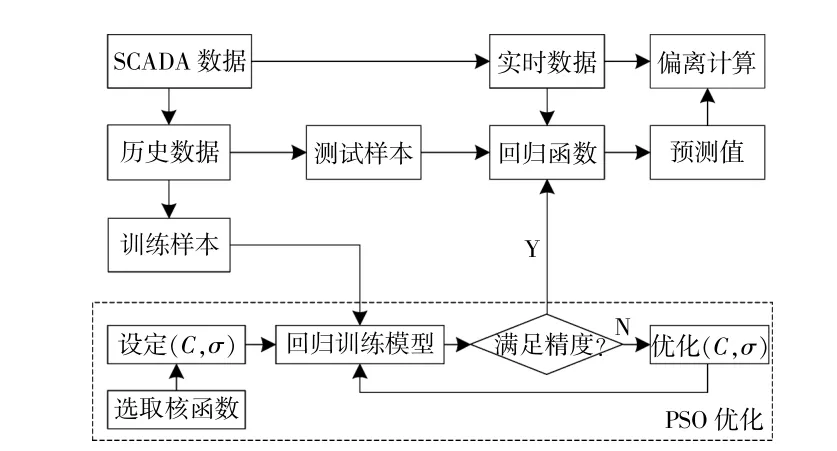
图5 基于SVR算法的参数偏离回归辨识Fig.5 Regression Identification of Parameter Deviation Based on SVR Algorithm

利用回归函数可计算出正常状态下的参数预测值。参数值偏离计算如下：

当 δ*偏 离 满 足 条 件：δP＞ηP＆δA＞ηA＆δCp＞ηCp（η*为偏离阈值），则可判定叶片出现结冰现象。

4 实测数据验证

4.1 SCADA相关参数辨识

选取宁夏某风电场结冰机组数据验证上述模型的正确性。机组主要参数：叶轮直径为110m，额定功率为2100kW，切入风速为3m/s，额定风速为10.5m/s，SCADA数据采集频率为1min。

4.1.1确定预测输入参量

随机取#A50机组连续5d的历史数据作为样本，依据皮尔逊积矩相关系数法，取｜r｜≥0.6（中、高相关程度）作为标准选取相关参数，计算各监测参数与有功功率的相关系数，得到变流器无功功率均值、发电量均值、风速1（机械式测风仪）均值、风速2（超声波式测风仪）均值、30s风速均值、5min风速均值、轮毂转速均值、发电机转速均值、转 矩 反 馈 平 均 值、电 网 电 压AB（BC，CA）均值、电网A（B，C）相电流均值、电网线电压L1L2（L2L3，L3L1）均 值、电 网 出 口 线 电 流L1（L2，L3）均 值 和 塔 架 振 动 加 速 度 均 值（波 段5，6，7，8，9，11，12）与有功功率输出量相关的输入参量。

考虑到机组相关变量数据具有不同单位和量级，且指标之间的量值差异非常大，为保证预测结果的准确性，需要对原始数据进行归一化[0，1]处理。

4.1.2选取验证数据

运行记录显示，#A50机组在20170319出现叶片结冰现象，并在19：56停机。由于没有安装任何监测叶片结冰的软、硬件设备，无法准确确定风力机叶片开始结冰的时间。鉴于此，本文选取机组SCADA系 统 在20170319T00：00-19：56的 监 测 数据作为分析、验证数据。

4.1.3输出功率数据辨识结冰

图6（a）为SCADA记录的有功功率1440个数据点以及应用回归预测计算出的相应功率值，图6（b）为 其 部 分 时 段 数 据。从 图6（b）可 知，大 约在460点之后，预测值开始偏离SCADA记录值。

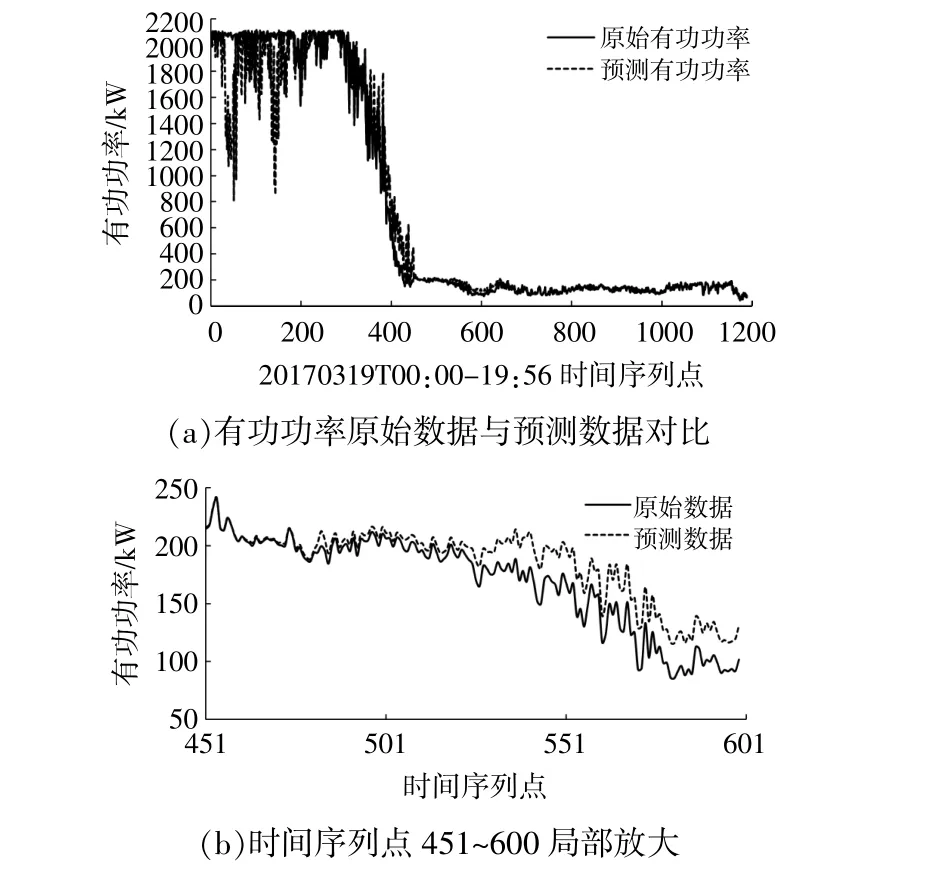
图6 有功功率预测值与原始值对比Fig.6 Compare the predicted value of active power with the original value

图7为机组有功功率的相对误差曲线。由图7可知，自458点之后，功率损失持续上升，即20170319T07：37前后发生“可能因叶片结冰”导致的机组整体性能“异常”。

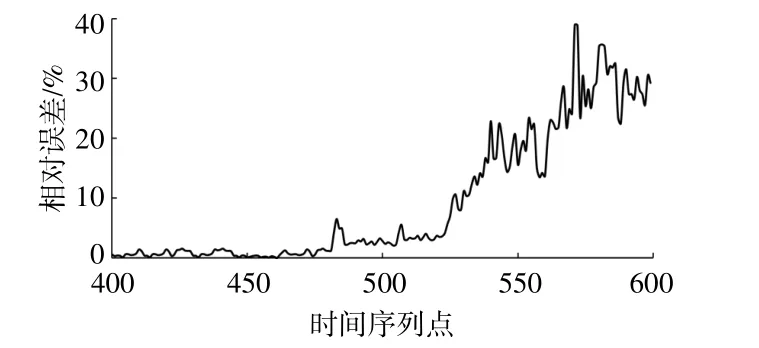
图7 有功功率400～600序列点相对误差Fig.7 Active power400～600sequence point relative error

4.1.4Cp数据辨识结冰

根据所选SCADA验证数据，计算机组Cp时序 值（图8）。

对比表3工况划分与图8，#A50机组处于两种 状 态，[1～342]时 序 点 间 处 于 第 一 状 态，[343～1440]时序点间处于第二状态。

[1～342]时 序 点 间，风 速 为10.5m/s，机 组 处 于Ⅳ工况区，叶轮转速、Cp，β正常波动变化，机组正常运行。

[343～1440]时 序 点 间，风 速 由10.5m/s逐 步降 低 到4.198m/s，之 后[443～1440]时 序 点，风 速 持续波动在4.198～10m/s，正常状态下机组应处于Ⅱ工况区，即Cpmax阶段，β不变，发电机转速跟随风速而变化。

图9为[400～600]数据时序点对应的多个参数值。

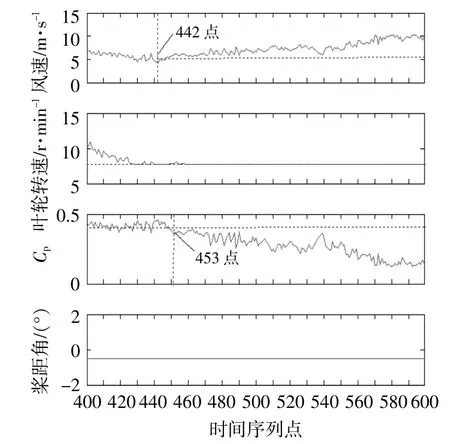
图9 时序400～600点间参数值Fig.9 Parameter values of sequence points in 400～600interval

由图9可知，[442～600]区段风速从4.198m/s开始持续增大，机组理应处于Cpmax，但与[400～452]区段不同的是，图中自453点开始，Cp出现快速下降，表明机组于时序453点即20170319T07：32时刻起，开始出现气动方面“异常”。

4.1.5振动特征数据辨识结冰

将塔架振动（振动加速度平均值）信号数据应用EEMD分解，选取前3个IMF特征信号进行分析（图10）。

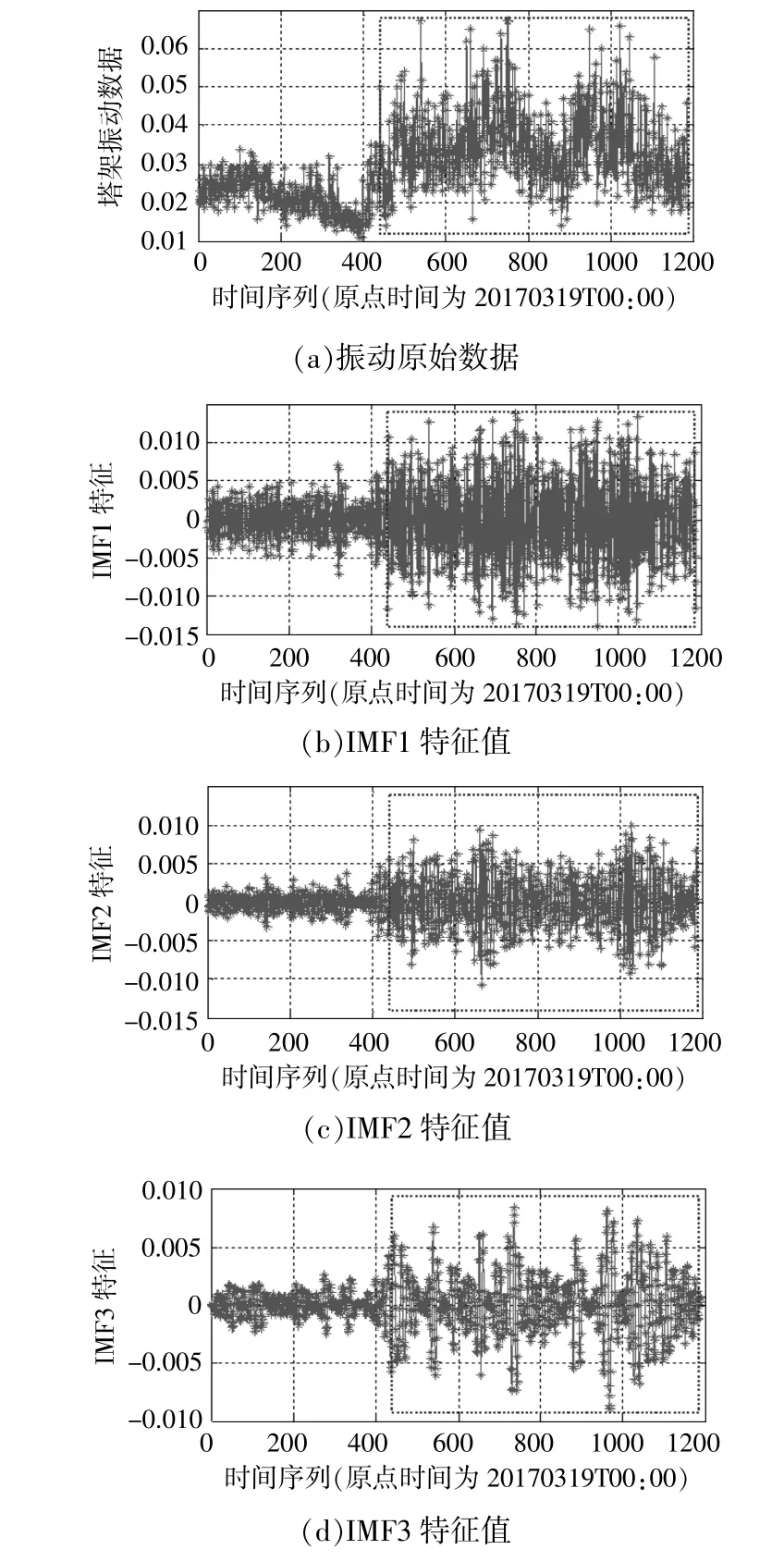
图10 EEMD信号特征分解图Fig.10 EEMD signal characteristics decomposition diagram

由图10可知，3种不同频率信号在441点附近的幅值都各自发生突然增大现象，即机组塔架于20170319T7：20左右，出现塔架振动＂异常＂现象。

上述3种模型计算结果对比如表5所示。

表5 3种SCADA参量对比判定机组叶片结冰Table5 Comparison of three SCADA parameters to determine the blade icing of WT

表5中，3种参量计算结果表明，#A50机组大约从450点开始出现运行异常，即叶片结冰。相对于机组输出功率来说，振动信号更加敏感，感知叶片结冰时刻更早一些。

4.2 不同类型风速测量仪验证

机组#A50共安装了机械式和超声波两种类型风速仪，两种测速仪实测风速数据如图11所示。

图11 两种风速测量仪的测量值对比Fig.11 Comparison of measured values between the two kinds of anemometer

由图11（a）可知：正常情况下，机械式测速仪和超声波测速仪所测得的风速值差别不大、趋势一致；在序列点[442～527]区域附近，叶片结冰之前，机械式比超声波式所测风速值偏大，但结冰之后则相反[图11（b）]。不考虑测速仪发生机械类故障，则可以推定是受结冰摩擦，影响到机械测量值。这也间接印证了#A50机组于时间序列第450点附近出现了结冰现象。

5 结论

①与通过观察机组功率曲线这种单一检测手段相比，本文采用多参数组合验证方法，可在叶片出现结冰的30min内辨识出叶片结冰，便于及时采取相应的运维决策。

②对比分析机组输出功率、风能利用系数和塔架振动信号3种参量的异常时序，机组塔架振动信号更加灵敏，可以更早反应叶片表面出现覆冰现象。

③通过分析叶片结冰前后SCADA有关参数的变化特性而不是通过增加硬件的检测方法，避免了因增添设备而改变叶片的气动特性、增加维护维修复杂度和运行成本。