基于分数域加窗和对比度增强的路面裂缝检测
赵鸿图, 周秋豪
(河南理工大学物理与电子信息学院, 焦作 454003)
裂缝是路面最为常见的病害之一,也是路面遭到损害的初期表现形式[1]。路面裂缝会导致路面的承载能力下降,如果不能及时被发现并养护,将会给行车安全带来严重隐患。而随着道路里程的增加和使用年限的延长,路面早期裂缝的防治工作变得愈加困难,传统的人工检测已经不再适应快速发展的道路养护需求。自20世纪80年代以来,国外的一些研究者就运用光学技术和计算机技术,先后制造出了基于激光测距和基于数字图像处理的路面裂缝检测设备,在一定程度上减少了人工干预,提高了自动化检测水平。而中国在这方面的研究虽然起步较晚,但目前也掌握了世界先进水平的自动化检测技术[2-3]。
随着数字图像处理技术的迅速发展,自动化检测程度得到了不断的提高,这为路面裂缝识别提供了更高效、更精确的检测方法[4]。贺福强等[5]采用网格聚类结合区域增长的方法来检测裂缝,提高了裂缝分割的质量。陈健昌等[6]和张世瑶等[7]采用深度学习的方法通过特征提取和模型训练来进行裂缝检测,一定程度上提高了检测效率并降低了检测成本。这些方法都只在空域对图像进行处理,而图像的频域中也包含丰富的特征信息,若同时在空域和频域进行处理将有助于裂缝提取,从而进一步提高检测精度。近年来,分数阶傅里叶变换[8]因其具有变换阶次的特殊性,能够同时反映出空域和频域的特征,被一些学者应用到图像识别领域。Kumar等[9]通过分数阶傅里叶变换和分数阶微分来检测图像的边缘,在分数频域中对图像进行处理,并且验证了其实用性。周丽军等[10]通过分数阶傅里叶变换将隧道裂缝图像转化到分数频域,先利用不同的阶次来均衡图像背景的对比度,然后使用分数阶微积分方法对图像进行增强来提取隧道裂缝。王永会等[11]使用二维分数阶傅里叶变换将裂缝图像从空域转换到分数域中,通过对频谱图进行区域去除和增强处理,从而达到了去除背景噪声的效果,为裂缝提取提供了便利。
在现实中,当裂缝位于复杂路面背景下或采集的裂缝图像光照不均匀时都会影响裂缝的提取,此时需要通过对比度增强处理来突出裂缝区域。而同态滤波算法因其具有良好地削弱低频、增强高频的能力,被广泛应用到图像对比度增强领域。如汪秦峰等[12]利用同态滤波来消除光照不均匀的雾霾图像所出现的光晕现象。而针对同态滤波算法中傅里叶变换只能单一地将图像从空域转换到频域的局限性,张新明等[13]将同态滤波与多级小波分解进行结合,用来增强图像的对比度。姜吉荣[14]也通过将傅里叶变换替换为小波变换来改进同态滤波算法,实现增强亮度不均匀裂缝图像的对比度,从而突出裂缝区域。
基于以上的研究,不同于传统方法在单一域内对图像进行处理,在分数域,即同时在空域和频域,现对裂缝图像进行去噪和对比度增强,并提出一种基于分数域加窗和对比度增强的路面裂缝检测方法来提取裂缝图像中的裂缝区域。该方法使用分数阶傅里叶变换在分数域进行加窗实现裂缝图像去噪,并通过改进同态滤波方法在分数域进一步对去噪图像进行对比度增强,以期最终达到有效提取裂缝特征的目的。
1 分数域加窗去噪
1.1 分数阶傅里叶变换
分数阶傅里叶变换可以将图像从空域转换到空频平面,同时反映图像的空域和频域信息,这将有利于全面分析图像的局部细微特征。二维分数阶傅里叶变换(two dimensional fractional Fourier transform,2D-FRFT)及其逆变换形式[15]分别如式(1)和式(3)所示,在p1、p2给定的情况下,图像f(x,y)的二维分数阶傅里叶变换定义为
(1)
式(1)中:Kp1,p2(x,y,u,v)为二维分数阶傅里叶变换的核函数,其定义为
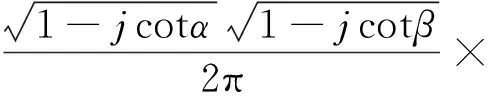
(2)
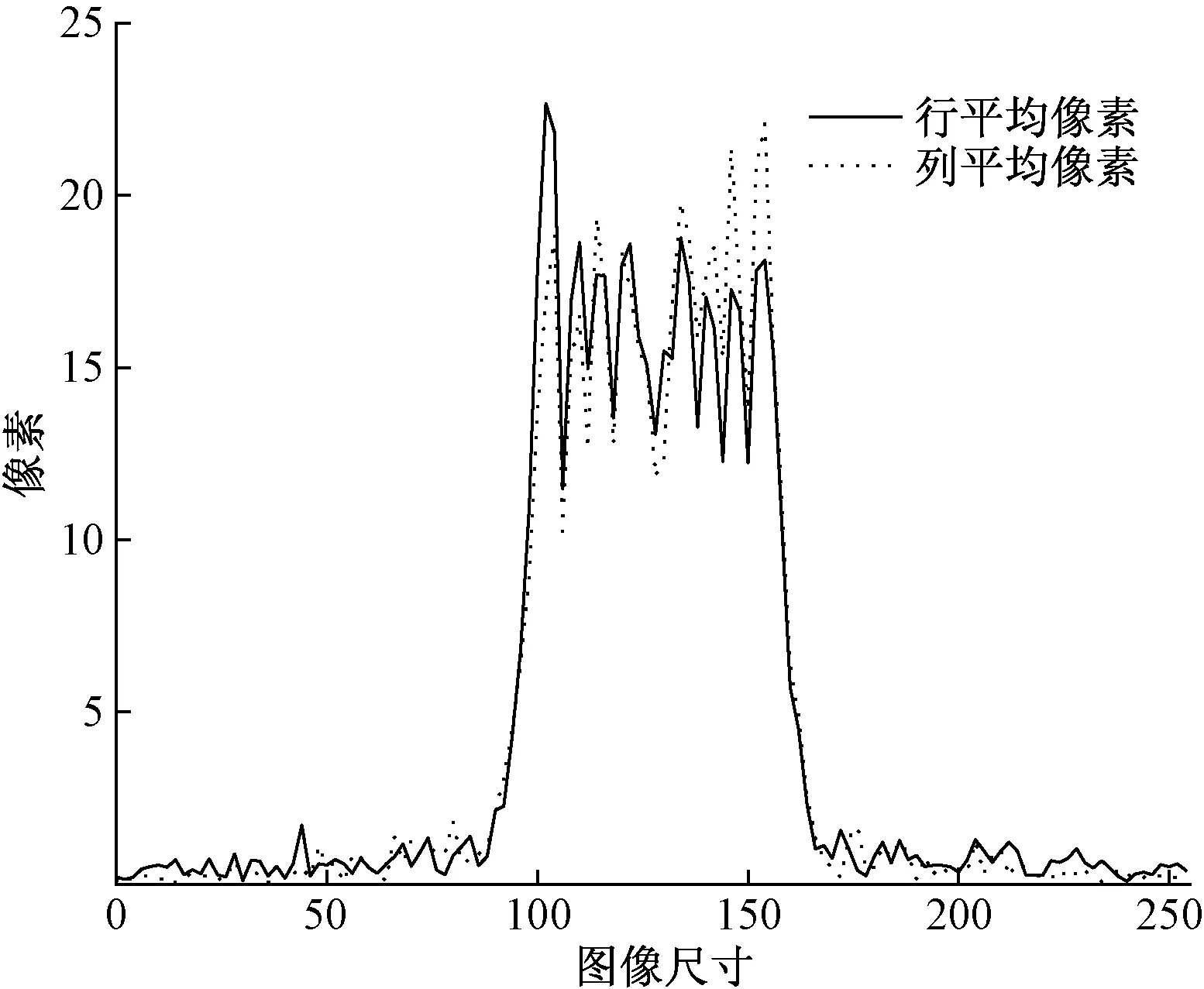
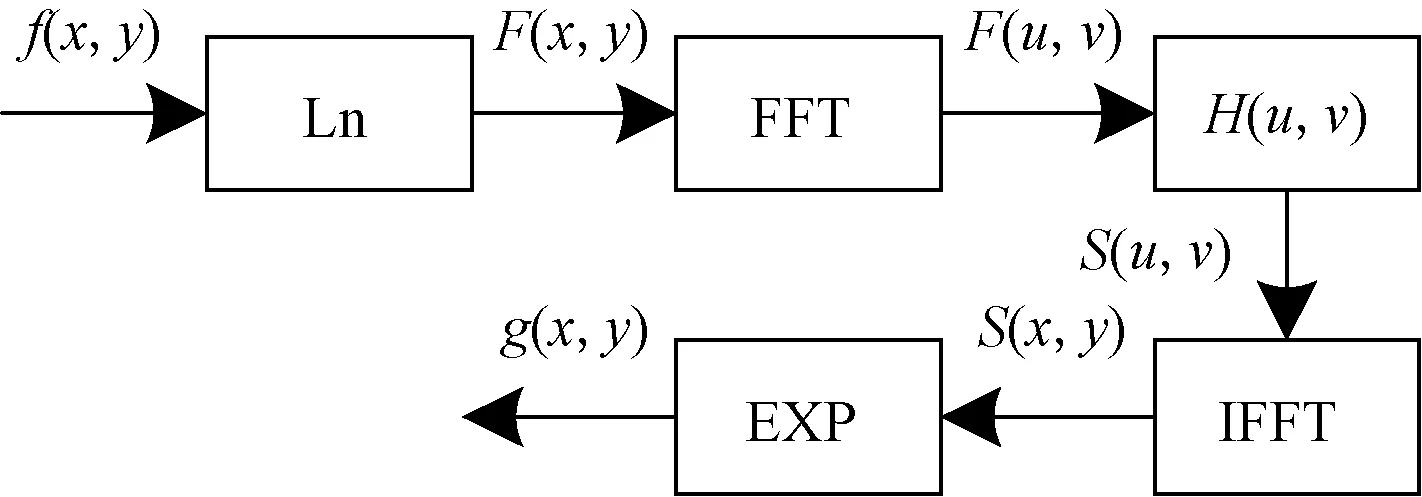
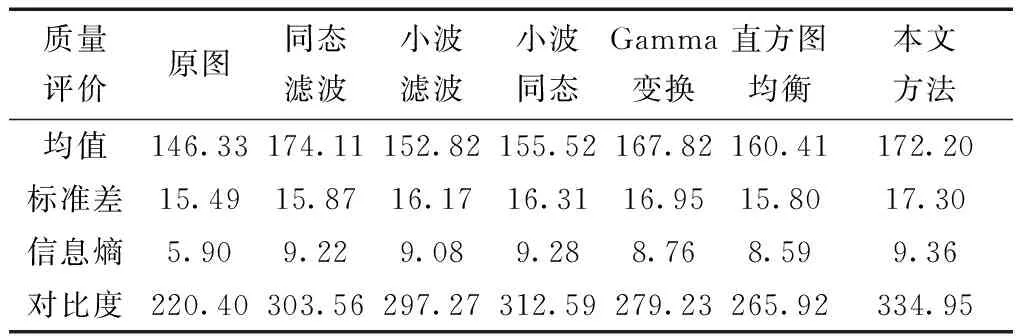
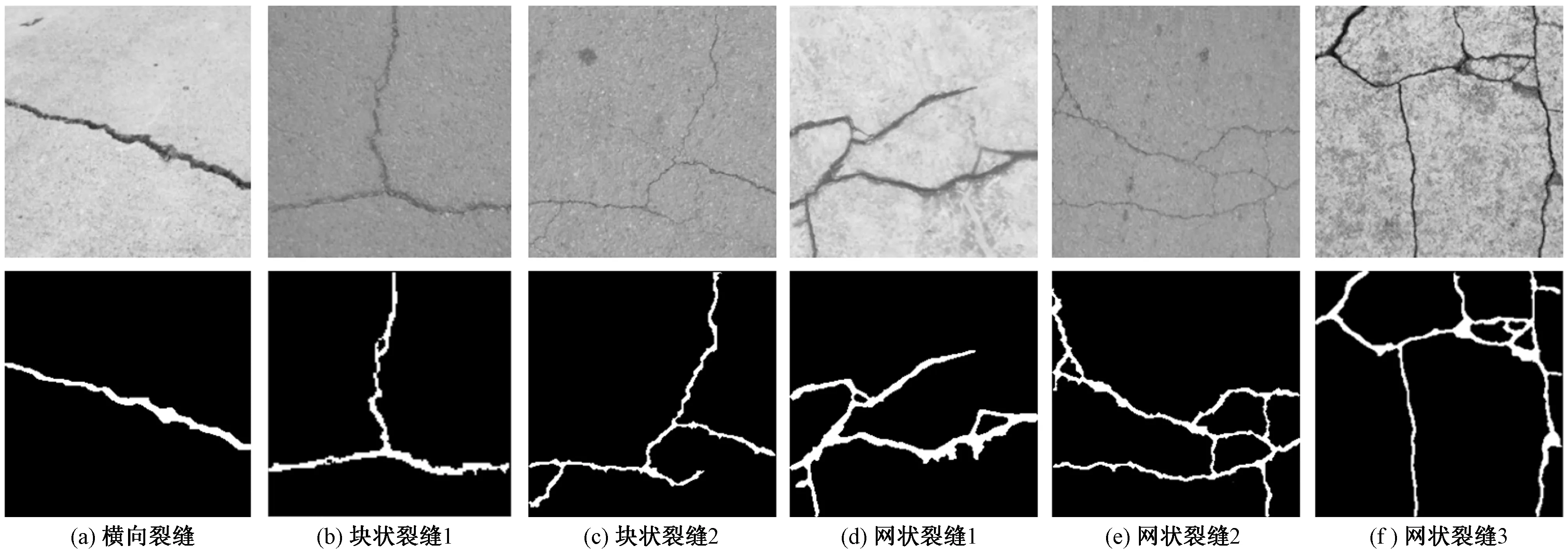
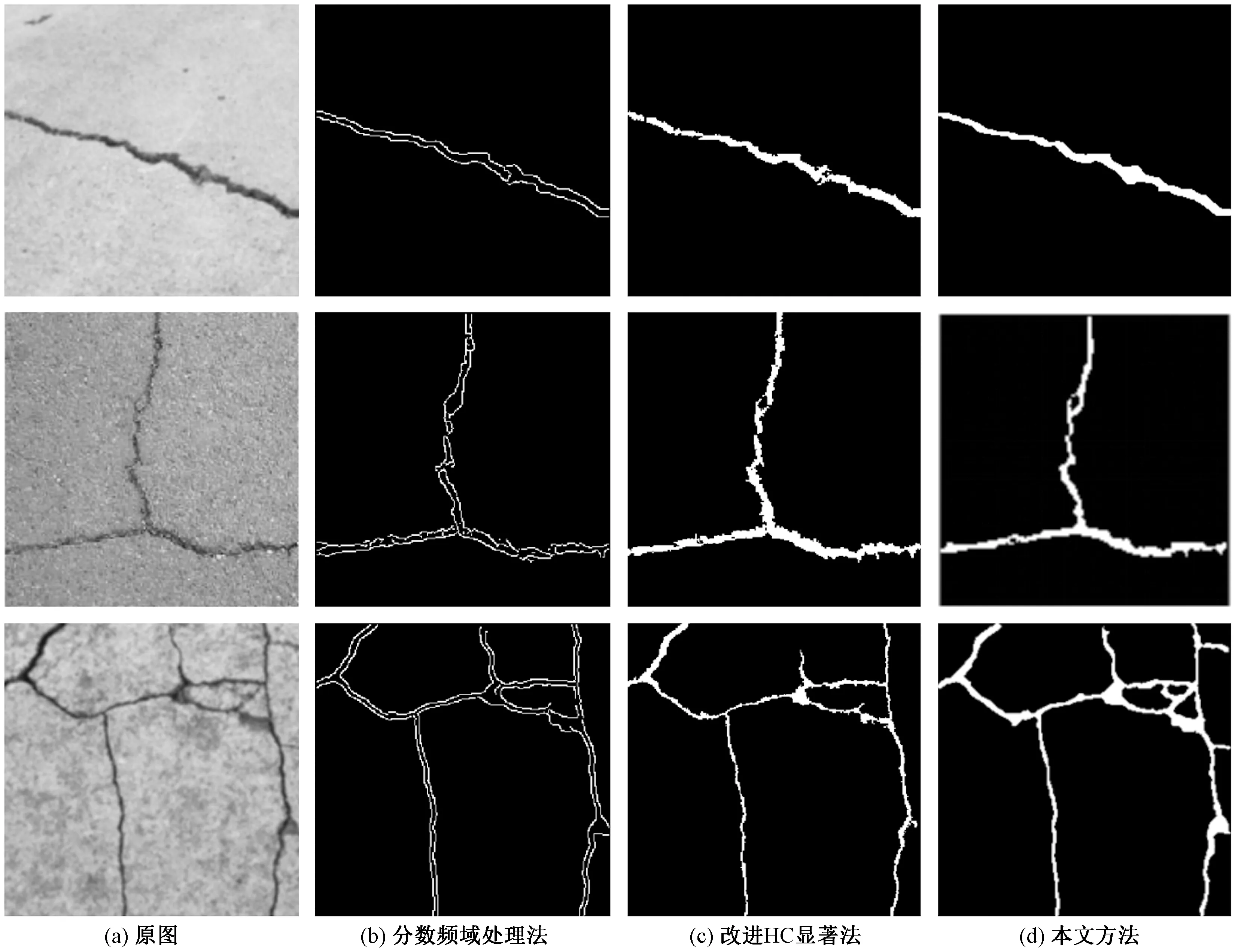
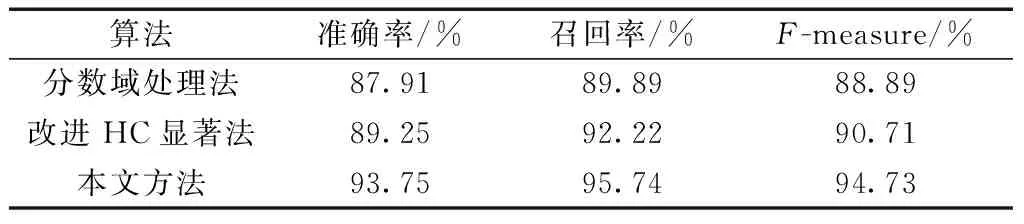
当α=β=0,即p1=p2=0时,表示图像的空域特征;当α=β=π/2,即p1=p2=1时,转化为传统傅里叶变换;当0<α=β<π/2,即0 二维分数阶傅里叶逆变换定义为 (3) 分数阶傅里叶变换具有集中信息的特征[16],当变换阶次p1、p2达到0.7时,分数域中心1/4区间内信息已集中到90%以上。继续增大p1、p2,频域所包含的信息增大的幅度和空间都会急剧减小,甚至会出现负增长。通过对横向裂缝、纵向裂缝、块状裂缝和网状裂缝图像集进行不同阶次的分数阶傅里叶变换后的结果进行比较发现,当p1、p2为0.83时对频谱图进行处理能够得到更好的效果。原始图像和0.7阶次、0.83阶次下的频谱图像如图1所示。 图1 原始图像和频谱图像Fig.1 Original image and spectrum image 为了更直观地表示,计算出图1(c)中频谱图像行和列的平均像素值,其分布图如图2所示。 图2 频谱图行列平均像素分布图Fig.2 Distribution map of average pixel values of the rows and columns of the spectrogram 根据上述二维分数阶傅里叶变换理论和图2可得到以下结论。 (1)对于裂缝图像转化的频谱图像,越靠近中心的区域,包含的裂缝特征信息就越多;越远离中心的区域,噪声信息越多。 (2)频谱图中较亮的“十字形”区域表示裂缝信息及原图中像素值较高、无法轻易消除的噪声。 (3)频谱图像素值较低,即亮度较暗的区域并不只包含噪声信息,也包含部分裂缝信息。 1.2.1 窗函数的设计 若要更好地去除原始裂缝图像中的噪声信息,在对频谱图进行处理时,要满足以下两个条件:①要最大程度地保留中心像素值较高的区域;②要较少地保留靠近边缘像素值较低的区域。 为同时满足这两个条件,使用分数域加窗的方法来处理频谱图。对频谱图中心包含裂缝特征信息较多的区域予以保留;对剩余区域使用升余弦窗函数[17]进行处理,使得越靠近边缘的区域保留越少。设计窗函数W(n)表达式为 (4) 式(4)中:N为频谱图的尺寸大小;m1和m2分别为保留中心区域的起点与终点;a为控制边缘区域像素值衰减速度的参数,且0≤a≤1。不同a取值下窗函数W(n)的形状如图3所示。 图3 不同a取值下的窗函数形状Fig.3 Shape of window function under different a value 1.2.2 最佳a的确定 由图3可知,随着a的增大,窗函数两侧衰减的速率越小,对应频谱图边缘区域保留的越多。而使用二维分数阶傅里叶变换加窗方法处理裂缝图像的目的是利于提取裂缝信息,去除噪声信息。因此,存在一个最佳的a,使得处理后两者的比值Ra达到最大,则有 (5) 式(5)中:Ncrack为图像中裂缝区域的像素点数;Nnoise为噪声像素点数。 经过Wa(n)处理后的频谱图2DFRFTW的表达式为 (6) 式(6)中:2DFRFT为二维分数阶傅里叶变换后的频谱图;2DFRFT(b)为频谱图的第b行,b=1,2,…,N;Wa(n)为最佳a值下的窗函数;符号·表示矩阵对应元素相乘。 综上,分数频域加窗去噪的流程如图4所示。 同态滤波算法[18]是一种频域图像增强的算法。它将频率过滤和灰度变换结合起来,以照度反射模型作为基础,在频域中同时压缩图像的亮度范围和增强图像的对比度,可以有效地解决图像中因照度不均匀及动态范围过大对图像处理带来的问题,并且能够在不损失亮区细节信息的同时,有效地增强暗区的细节信息,克服了直接用傅里叶变换处理造成的图像失真和细节丢失的问题[19],同态滤波算法流程如图5所示。 图4 分数域加窗去噪流程Fig.4 Process of fractional frequency domain windowing for removing noise f(x,y)为输入图像;Ln为对数变换;F(x,y)为f(x,y)对数变换后的图像;FFT为傅里叶变换;F(u,v)为F(x,y)傅里叶变换后的图像;H(u,v)为同态滤波传递函数;S(u,v)为H(u,v)F(u,v);IFFT为傅里叶反变换;S(x,y)为S(u,v)傅里叶反变换后的图像;EXP为指数运算;g(x,y)为指数运算后最终得到的同态滤波增强图像图5 同态滤波流程图Fig.5 Homomorphic filtering process 而传统傅里叶变换处理图像时,只能单一地将图像从空域转换到频域,但是当图像在空域和频域都难以辨别其特征时,傅里叶变换将不再适用。针对这一局限性,引入了具有变换阶次的分数阶傅里叶变换,将分数阶傅里叶变换与同态滤波算法相结合,在分数域对图像进行对比度增强处理,其增强效果强于传统的频域增强。改进后的算法如下。 步骤1对使用分数频域加窗去噪的图像fa(x,y)进行分解。表达式为 (7) 式(7)中:i(x,y)为照射分量,具有变化缓慢的特征,在频谱中主要集中在低频区域;r(x,y)为反射分量,倾向于剧烈变化,特别是在不同物体的交界处,其在频谱中主要集中在高频区域。对式(7)两边同时取对数,则有 ln[fa(x,y)]=ln[i(x,y)]+ln[r(x,y)] (8) 步骤2利用式(8)的形式将图像的照射分量和反射分量分离,再对式(8)进行分数阶傅里叶变换,将这两个分量转换到分数域来处理,则有 (9) H(u,v)Rp(u,v) (10) (11) 即 (12) 步骤3最后对式(12)两边同时进行指数运算,得到增强后的图像,即 g(x,y)=efah(x,y)=eih(x,y)erh(x,y) =i0(x,y)r0(x,y) (13) 式(13)中:i0(x,y)和r0(x,y)分别为增强后图像的照射分量和反射分量。 传递函数H(u,v)通常选用巴特沃斯高通滤波器(Butterworth high pass filter,BHPF),则H(u,v)为 (14) 为了得到更好的增强效果,利用低频增益rL和高频增益rH来修正传递函数,则有 (15) 式(15)中:D0为截止频率半径;D(u,v)为频谱图中点(u,v)到原点的距离;n为阶数,通常取值为2。 综上,分数阶同态滤波增强算法流程如图6所示。 图6 分数阶同态滤波增强流程图Fig.6 Fractional homomorphic filtering enhancement process 使用分数阶同态滤波处理裂缝图像的目的是突出暗部的裂缝特征,提高裂缝图像的对比度。因此,存在一个最佳阶次p,使得分数阶同态滤波处理后图像的对比度达到最大值。 在最佳阶次p下,定义最大对比度的计算公式为 (16) 式(16)中:k、l分别为分数阶同态滤波增强图像中两个相邻像素的灰度值;φ(k,l)=|k-l|为相邻像素间的灰度差;Pφ(k,l)为灰度差为φ的像素分布概率。 综合上述对算法的描述和改进,对裂缝图像增强的具体过程如下。 步骤1首先使用分数阶傅里叶变换加窗去噪得到输入图像fa(x,y),再对fa(x,y)进行对数变换将图像的照射分量和反射分量分离,得到ln[fa(x,y)]。 步骤3取阶次p=-p0对Sa(u,v) 进行分数阶傅里叶逆变换转回到空间域,得到Sa(x,y);最后对Sa(x,y)进行指数运算,得到分数阶同态滤波后增强的图像g(x,y)。 基于分数阶同态滤波算法增强图像的流程图如图7所示。 图7 图像增强流程图Fig.7 Image enhancement process 图8 裂缝提取结果Fig.8 Crack extraction results 裂缝图像提取是将裂缝特征从背景中提取出来,图8选取一张横向裂缝图像(第一行)和一张块状裂缝图像(第二行)分别进行裂缝提取。其中,Canny边缘检测算法[20]能够比较准确地检测出裂缝的真实边缘,但可能将背景噪声也标识成边缘,检测图像如图8(a)所示。Otsu阈值分割法[21]可以有效地将裂缝特征与背景分割开,但二值化后的裂缝图像边缘会有较多的像素缺失,出现“锯齿”现象,甚至出现断连,即整体提取效果好,能提取出更细节的部分,而边缘提取效果较差,分割结果如图8(b)所示。 图像或运算是将两幅图像的对应像素按位进行或运算。将Canny边缘检测结果Ed和Otsu阈值分割结果Ts进行或运算,或运算OR公式为 (17) 或运算既保留了裂缝边缘的完整性,又能够很好地消除“锯齿”现象。或运算结果如图8(c)所示,通过或运算裂缝边缘缺失的部分将会被“包裹”,封闭了边缘“锯齿”状缺口。再对图像进行膨胀操作来填充一些细小的孔洞并桥接裂缝断连的部分,如图8(d)所示。然后对图像进行噪点去除,如图8(e)所示。最后通过双重腐蚀操作细化裂缝,就提取出较为完整的裂缝特征,如图8(f)所示。 以MATLAB 2019b为实验平台,以120张横向和纵向裂缝图像、112张块状裂缝图像和98张网状裂缝图像作为原始样本,将这330张尺寸不一的裂缝图像分割为256×256大小的500张子图像作为实验分析对象。所有实验仿真在IntelI CoreI i5-6300HQ CPU @ 2.30 GHz,运行内存8 GB的个人电脑中运行。 路面裂缝图像尺寸大小均为256×256,则N=256;经过测试得出,m1和m2的取值仅与选取的阶次有关,分数域去噪选取的阶次为p1=p2=0.83,由频谱图行列平均像素值分布图可以得到m1=93,m2=163。 为确保实验的准确性,取初始a=0,以0.01为步长迭代求得裂缝信息与噪声信息的比值Ra,直至a=1停止迭代。求得不同裂缝图像在各a取值下的Ra的曲线如图9所示,其中,比值Ra越大,去除噪声信息的效果越好。 图9 求最佳a取值图Fig.9 Find the best value of a 使用最佳a取值下的窗函数Wa(n)对频谱图进行处理,通过分数阶傅里叶逆变换得到去噪后的裂缝图像。将加窗处理的图像与文献[11]中的加矩形窗处理的图像进行对比。为了更直观地显示去除噪声信息的效果,将去噪前后的裂缝图像进行二值化处理,去噪对比结果如图10所示。 图10 去噪前后对比图像Fig.10 Contrast image before and after removing noise 根据图10可以得出,由于加矩形窗处理没有考虑到频谱中心之外的区域也包含部分裂缝信息,导致去噪时将裂缝信息特征也去除了。而本文加窗方法则可以在不破坏裂缝信息的情况下去除原始图像的大部分噪声信息,但是一些与裂缝信息特征很接近的噪声信息无法被轻易消除。因此,为提取完整的裂缝信息,将通过增强裂缝特征与背景和剩余噪声的对比度来突出裂缝区域,以便于后续裂缝信息提取。 由于变换阶次p达到0.7时,分数域中心1/4区间内信息已集中到90%以上,因此,取初始阶次p=0.7,对不同裂缝图像进行分数阶同态滤波增强处理。然后,以0.01为步长迭代求得各阶次下增强图像的对比度,直至p=1停止迭代。求得各阶次下的图像对比度值的曲线如图11所示。 空心图案表示该曲线的最值点图11 求最佳阶次pFig.11 Find the best value of p 由表1可知,6种算法都不同程度地提升了图像的均值、标准差、信息熵和对比度。其中,同态滤波增强图像的均值最大,说明增强后的图像亮度最高,但单独使用同态滤波和小波滤波增强的图像在标准差、信息熵值和对比度上都低于两者结合的小波同态滤波算法。这是由于小波分解的子波通过同态滤波中的高通滤波器后,高频的裂缝部分细节得到增强,同时低频的背景受到削弱,因此增强效果较好。本文方法在空域和频域进行增强高频削弱低频处理时,通过调节阶次大小,选取了增强后对比度最高的图像,因此增强效果最好。而Gamma变换扩展低灰度值的裂缝部分细节,增强了暗部区域的对比度;直方图均衡将裂缝区域的低灰度值进行展宽,增加了灰度值差别的动态范围,从而增强图像整体对比度。这两种方法都只对裂缝图像的局部区域进行处理,因此增强效果有限。 表1 各算法质量评价对比Table 1 Comparison of the quality evaluation of each algorithm 综合来看,本文方法增强后的图像均值略小于同态滤波方法,但其标准差、信息熵和对比度都优于其余方法,因此具有更明显的增强效果和最优的质量评价。这表明经过分数阶同态滤波增强后的裂缝图像对比度提高更多,细节信息也更加丰富,即裂缝区域更加突出了。 分别用Canny边缘检测算法、Otsu阈值分割法以及两者做或运算方法对上述去噪增强后的图像进行裂缝特征提取,实验结果如图12所示。其中,第一行表示不同类型和形状的原始裂缝图像,第二行表示使用本文方法最终得到的提取结果。 图12 裂缝特征提取结果Fig.12 Crack extraction results 将本文方法与王永会等[11]的分数频域处理法和钟艾娥的改进HC显著性检测法[22-23]的裂缝提取结果进行对比,并从实验样本中选取3张横向(第一行)、块状(第二行)和网状(第三行)的裂缝图像,对比结果如图13所示,并分别计算准确率、召回率和F-measure 3个指标[24]来评价各裂缝检测算法的性能,如表2所示。 图13 各算法检测结果对比Fig.13 Comparison of detection results of various algorithms 表2 各算法性能对比Table 2 Performance comparison of various algorithms 由图13可以看出,对于裂缝宽度较小的区域,本文方法能够在去除噪点的同时保留边缘完整连续的裂缝特征,而其余两种方法去除噪点的效果较差,并且提取的裂缝特征出现断连现象;对于复杂度较高的网状区域,前两种方法只能提取出外围的网状轮廓,不能提取出网状内部的细节部分,而本文方法则能够较为完整地提取出裂缝更为细节的区域。因此,本文方法具有更好的检测结果。 根据表2中的实验结果可知,3种裂缝检测方法的各个评价指标都高于85%,具有较高的准确率;而本文方法较分数域处理法和改进HC显著法在准确率上分别提升了5.84%和4.5%,在召回率上分别提升了5.58%和3.52%。 综合上述对各算法的裂缝提取效果和评价指标对比,本文方法裂缝提取效果更好,鲁棒性更高,性能更优。 针对复杂背景下路面裂缝检测,提出了一种基于分数域加窗和对比度增强的路面裂缝检测方法,并将该算法与分数频域处理法和改进HC显著法进行了定性定量地对比分析,仿真实验结果表明本文方法去除背景噪声效果和裂缝特征提取效果较好,能够有效提升裂缝的识别率。
1.2 分数域加窗


2 分数域对比度增强
2.1 分数阶同态滤波

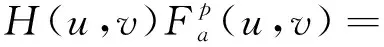
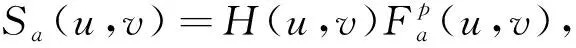
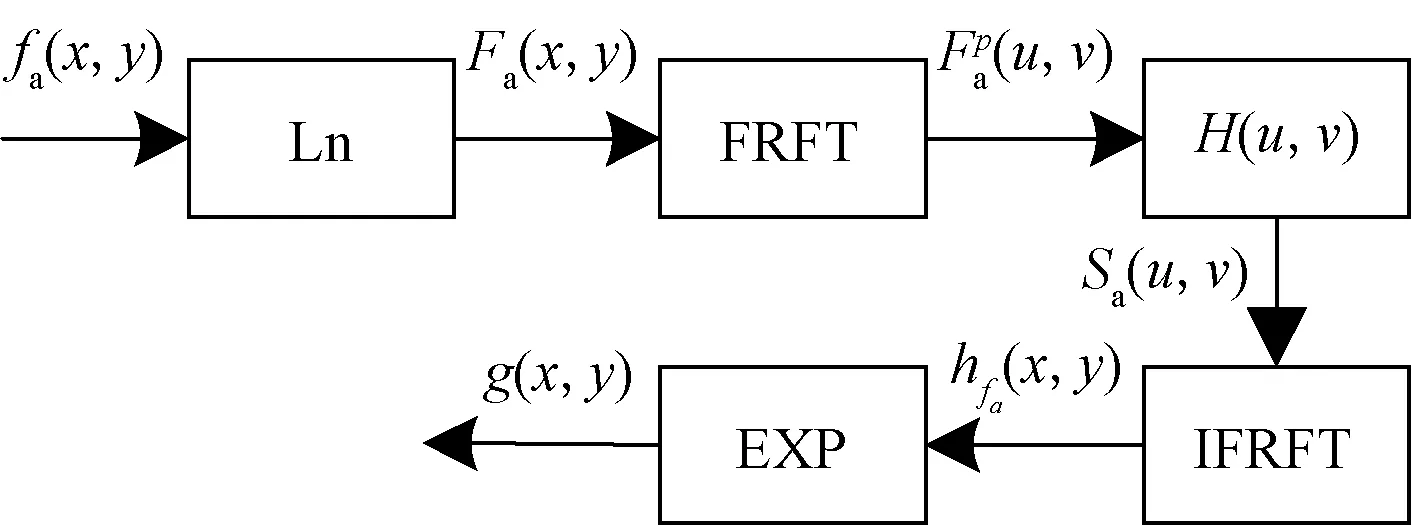
2.2 最佳阶次p的确定
2.3 图像对比度增强过程
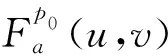
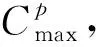

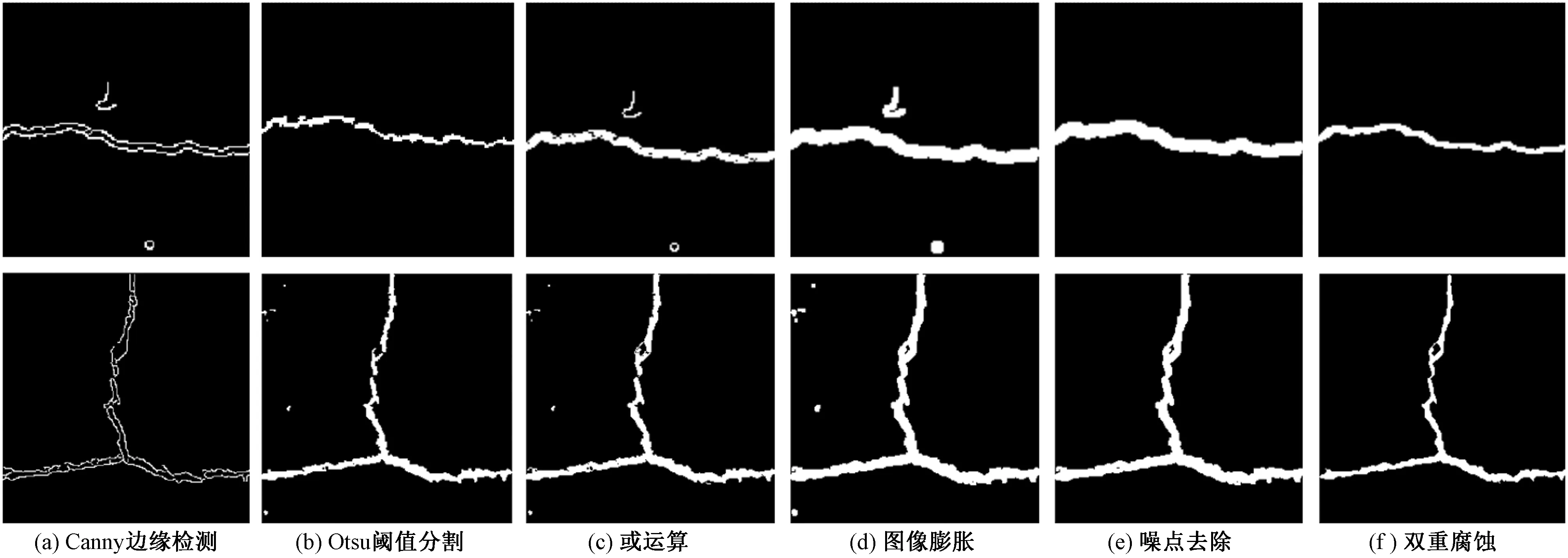
3 裂缝图像提取
4 实验仿真与结果分析
4.1 窗函数的最佳a确定

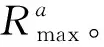
4.2 对比度增强的最佳阶次p
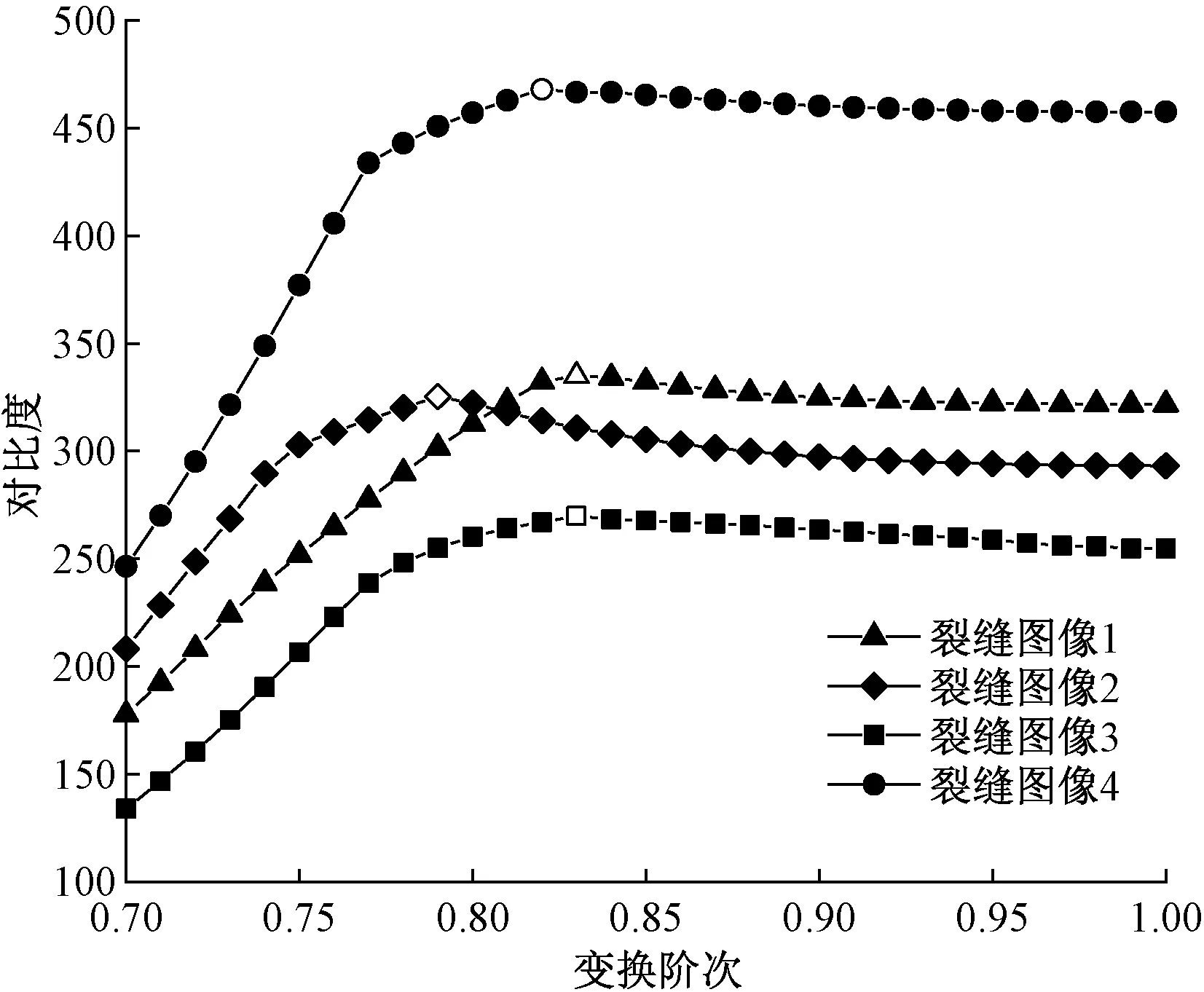

4.3 裂缝信息的提取
5 结论

