基于CFD仿真的扑动模式对扑翼气动性能影响研究

李战东,龚昌全，王 巍，陶建国

(1.沈阳航空航天大学 民用航空学院，沈阳 110136；2.哈尔滨工业大学 机电工程学院, 哈尔滨 150001)

1 引言

扑翼飞行器由于其独特的仿生外形和灵活的机动性，在军事和商业领域具有广泛的应用前景。扑翼飞行器的气动外形和运动方案是影响其气动性能的主要因素[1]。与传统飞行器相比，扑翼飞行器的运动主要由上下扑动、弦向扭转、展向折叠和前后挥摆几种运动耦合而成，产生飞行所需的气动升力和推力，从而使其具备灵活的机动性能[2]。因此，研究运动模式对扑翼气动性能的影响具有重要意义。

扑翼飞行的运动模式对飞行过程中高升力和高推力的产生具有重大影响。近年来，国内外的研究人员采用仿真计算和实验，研究了扑翼飞行运动参数的变化规律，以探索扑翼的运动模式对其气动性能的影响。对于刚性扑翼，研究人员通过将鸟类翅膀的上下扑动简化为二维翼型的沉浮运动,研究了运动参数对沉浮翼型产生推力大小的影响[3]，Yang等[4]将机翼置于二维层流中，通过改变扭转和水平挥摆运动之间的相位差，发现当扭转角为30°，扑翼会产生高平均推力，而较小幅度的水平扫掠运动有利于提升扑翼的推进效率，且随着挥摆运动幅度的增加，扑翼的升力也会随之小幅度增加；Xijun Ke等[5]通过引入俯仰频率与扑动频率的频率比值，研究了两自由度三维扑翼俯仰角相对扑动相位偏移的可调规律，Khanh Nguyen等[6]采用计算流体动力学方法研究了机翼运动学对悬停气动效率的影响，发现拍击和甩打可以提高5%的升力；M.M De等[7]研究了非对称1自由度运动扑翼模型在不同平面形状下的气动特性，发现椭圆形的翼面飞行效率更高；吴越等[8]采用了非定常涡格法(UVLM)计算扑翼气动力，发现经过优化后的扑翼运动方案能够使特定翼面发挥最佳的气动性能；Sang-Hoon Yoon等[9]开发了一种三维扑翼流固耦合求解器，发现被动扭转运动对弧面机翼气动性能有显著影响。谢鹏[10]基于ADAMS软件，设计了一种折叠翼仿鸟扑动飞行器，并发现折叠翼在上扑阶段受到更小的阻力，在扑动过程中能够获得更大的升力;Yang等[11]结合CFD数值计算方法，设计了一种具有完全自主操作的能力扑翼飞行器Dove，可实现半小时的巡航工作，并同时向4 km外的地面站发送实时稳定的彩色视频。扑翼的气动性能与附着在机翼表面的涡结构也密切相关，A.Boudis等[12]通过对二维两自由度非正弦运动轨迹扑翼模型的涡脱落过程进行研究，发现相比于正弦扑动轨迹，非正弦轨迹每半个周期可以脱落2个反向涡，且增大了尾缘涡的强度，显著提高了扑翼的推进效率。Chunlin Gong等[13]提出了一种基于浸没边界格子Boltzmann方法(IB-LBM)的大规模并行求解器，分析了三维扑翼前缘涡和尾流涡结构的演化过程，发现随着展弦比的增大，扑翼的推力系数先增大后减小。Deng等[14]搭建了六分力传感器测力实验分析了扑翼频率和机翼柔性对气动力的影响，然后使用粒子图像测速技术揭示了扑翼后缘涡的脱落过程，并发现无翼肋约束的机翼比有翼肋约束的气动性能更好。Yang等[15]通过数值模拟和实验研究了单自由度扑翼样机的气动机理，发现扑翼在升力方向上的惯性力大小与气动力的大小相同，而在推力方向上惯性力相对较小。

综上所述，目前绝大部分的研究都是基于单自由度和两自由度耦合运动模型展开，主要研究几何和结构参数设计对气动性能的影响，并没有完全揭示各个运动对气动机理的影响。同时，大部分研究都是基于二维翼型开展，忽略了三维仿生扑翼流场强烈的非定常效应、涡流动复杂的特点，没有精确揭示运动模式对扑翼气动性能的影响，而复杂涡系的精确捕捉是揭示扑翼飞行器产生高升力和大推力机理的重要基础。本文建立了三维扑翼多自由度运动模型，采用数值模拟的方法将计算模型导入CFD求解器中，对扑翼的非定常N-S方程进行求解，获得不同真实运动模式下翼的升力和推力数据，然后结合翼面压力场分布情况和流场涡结构的演变过程，对扑翼的升推力变化曲线、压力场和涡结构的结果进行分析讨论，进一步揭示各个运动模式对翅翼气动性能的影响。

2 数值计算模型和方法

2.1 计算模型

为了更真实的研究运动模式对扑翼气动性能的影响，本文采用NACA00012翼型建立三维扑翼模型，翼面布局形式为反齐默尔曼机翼，研究其在单自由度和多自由度下的升力性能和推力性能问题。整个扑翼模型和运动坐标系如图1和表1所示。

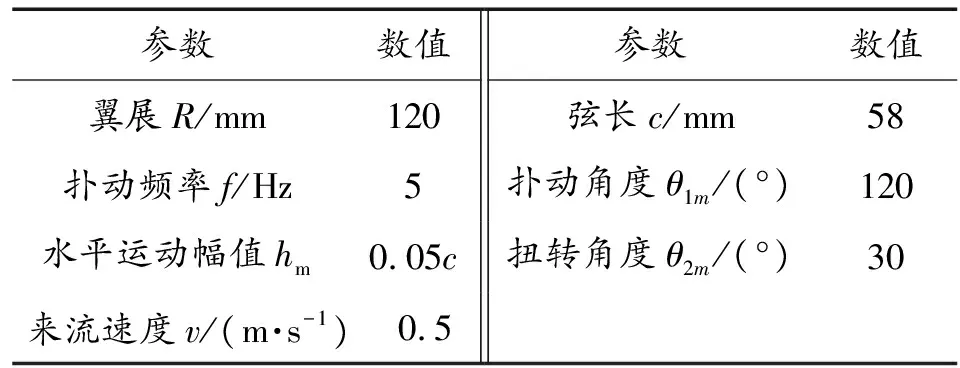
表1 三维扑翼的几何和运动学参数

图1 NACA0011三维扑翼模型

翅膀的扑动方式和扑动规律对鸟类飞行过程中高升力和大推力的形成至关重要。典型的鸟类翅膀宏观扑动包含扑动、扭转、扫掠和折叠。本文将主要研究YZ方向的扑动、弦向XZ面的扭转和水平XY面上的水平扫掠运动的耦合对扑翼气动性能的影响。扑翼飞行器翅翼的上下扑动运动简化为以X轴为旋转轴作扑动的简谐运动[4]，则翅翼的扑动规律方程为：

θ1(t)=θ1msin(2πft)

(1)

式中：θ1(t)为翅翼在垂直方向上的扑动角速度；f为扑翼运动的扑动频率；θ1m为扑翼运动的扑动幅值。

对于扑翼的弦向扭转运动，将其定义为以Y轴为旋转中心的扭转运动，简化后的扭转运动规律方程为：

θ2(t)=θ2 msin(2πft)

(2)

式中：θ2m扑翼弦向的扭转幅值。

对于扑翼的水平运动，将其定义为扑翼沿X轴方向的水平运动，简化后的水平运动规律方程为：

h(t)=hmcos(2kπft)

(3)

式中：h(t)为扑翼运动过程中，翅翼在水平方向上的位移；hm为扑翼运动的水平运动的幅值；k为扑翼水平运动的频率调控参数。

本文将θ1(t)的扑动运动定义为单自由度运动；θ2(t)的扭转运动和θ1(t)扑动的耦合运动定义为两自由度运动；θ1(t)的扑动运动、θ2(t)的扭转运动和h(t)水平运动共同控制的耦合运动定义为3自由度运动。

2.2 数值计算方法

基于图1的三维扑翼模型，在开展扑翼运动数值计算模拟时，确定翅翼各个自由度的运动参数如下：翅翼的扑动幅值为120°，扭转幅值为30°，扭转中心为1/5c，扑翼运动频率为f=5 Hz，水平运动的幅值为0.05c。考虑到流动对气动性能的影响，计算域的大小为13c×8c×8c，边界条件的设置如图2所示。网格划分由ICEM CFD软件完成，采用四面体非结构网格来离散流体域，并对近机翼表面进行加密处理，通过计算网格总数量为118万，最差网格质量为0.35，满足计算精度要求。

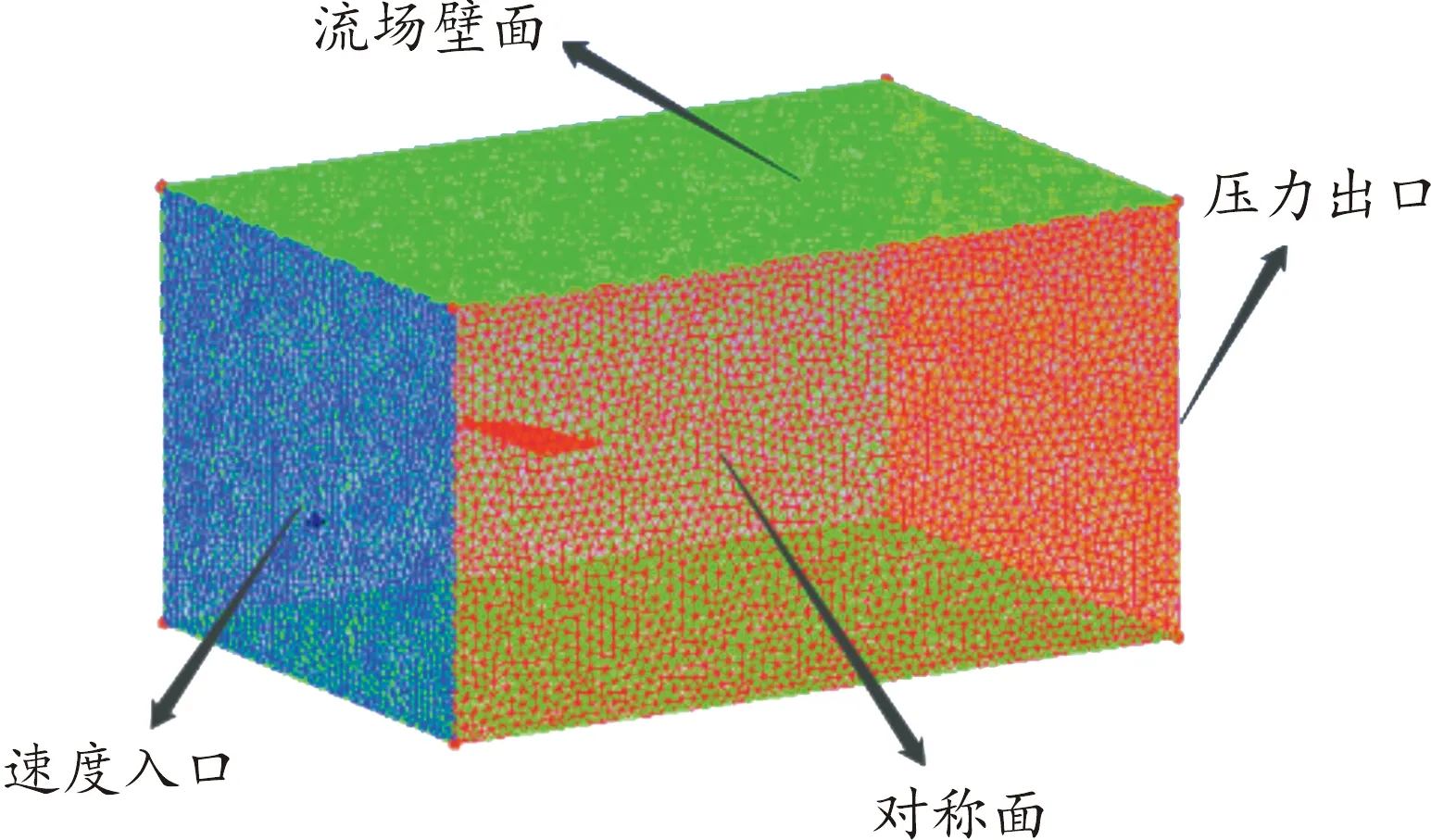
图2 流域网格划分及边界条件设置

随着网格精度的提高，研究计算结果的收敛性是至关重要的，因此，通过改变计算域网格的数量，对扑翼的计算结果进行了网格无关性验证，为此还考虑了网格数量为57万和271万的计算结果，得到一个周期内不同网格密度随时间的升力变化曲线如图3所示。从图3中可以看出，采用网格数量为57万和271万所得的升力数据计算结果变化曲线与网格数量为118万的计算得到了较好的吻合，这表明本文的扑翼数值计算结果基本不受网格密度变化的影响。

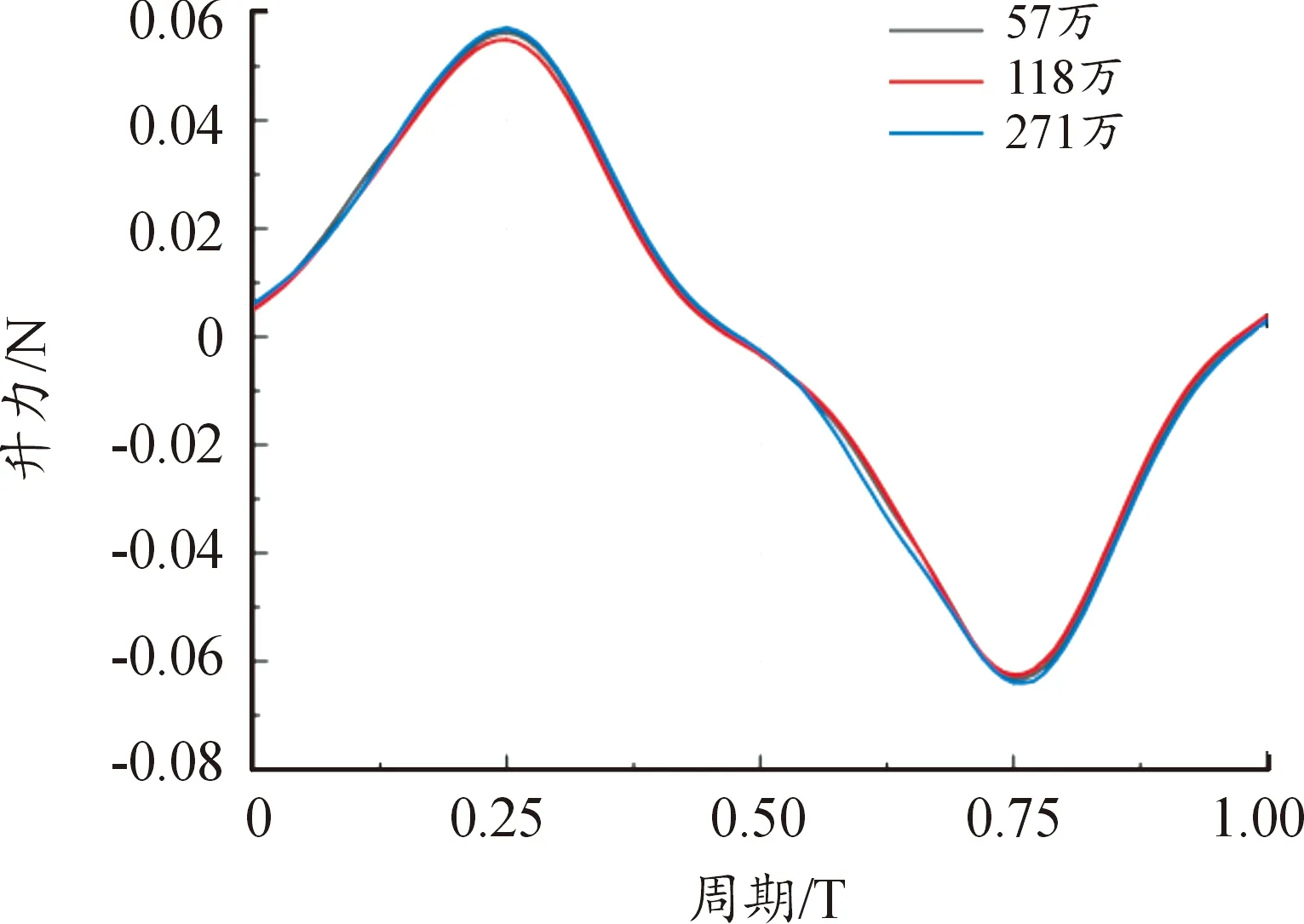
图3 不同网格精度下的气动力变化曲线

湍流模型采用Realizableε-epsilon模型，扑翼的流体控制方程采用有限体积法进行求解，其中控制方程中非定常项采用1阶隐式格式进行离散，对流项采用2阶迎风格式进行离散，扩散项采用中心差分格式进行离散，速度和压力的解耦采用SIMPLEC算法实现，然后结合网格光顺和重构的动网格技术，分别对不同自由度的扑翼运动模型进行仿真计算，得到扑翼的升力变化曲线和推力系数变化曲线。扑翼的推力系数定义为：

(4)

式中：FT为扑翼推力；ρ为扑翼周围空气密度；S为扑翼面积。

数值计算中，采用有限体积法，通过ANSYS FLUENT软件对上述的控制方程进行数值仿真。扑翼模型的运动通过用户自定义方程(UDF)控制实现。

2.3 气动力方法验证

为了验证本文气动力计算方法的准确性，本文根据Yang[15]对扑翼样机Dove的实验数据，建立了几何参数和运动学参数一致的扑翼模型，其中翼展R为300 mm，弦长c为100 mm，扑动角度为70°，扑动频率为6 Hz；运用本文的气动力计算方法和运动模型对扑翼的气动性能进行仿真计算，得到对应扑动行程的实验数据对比结果如图4所示。

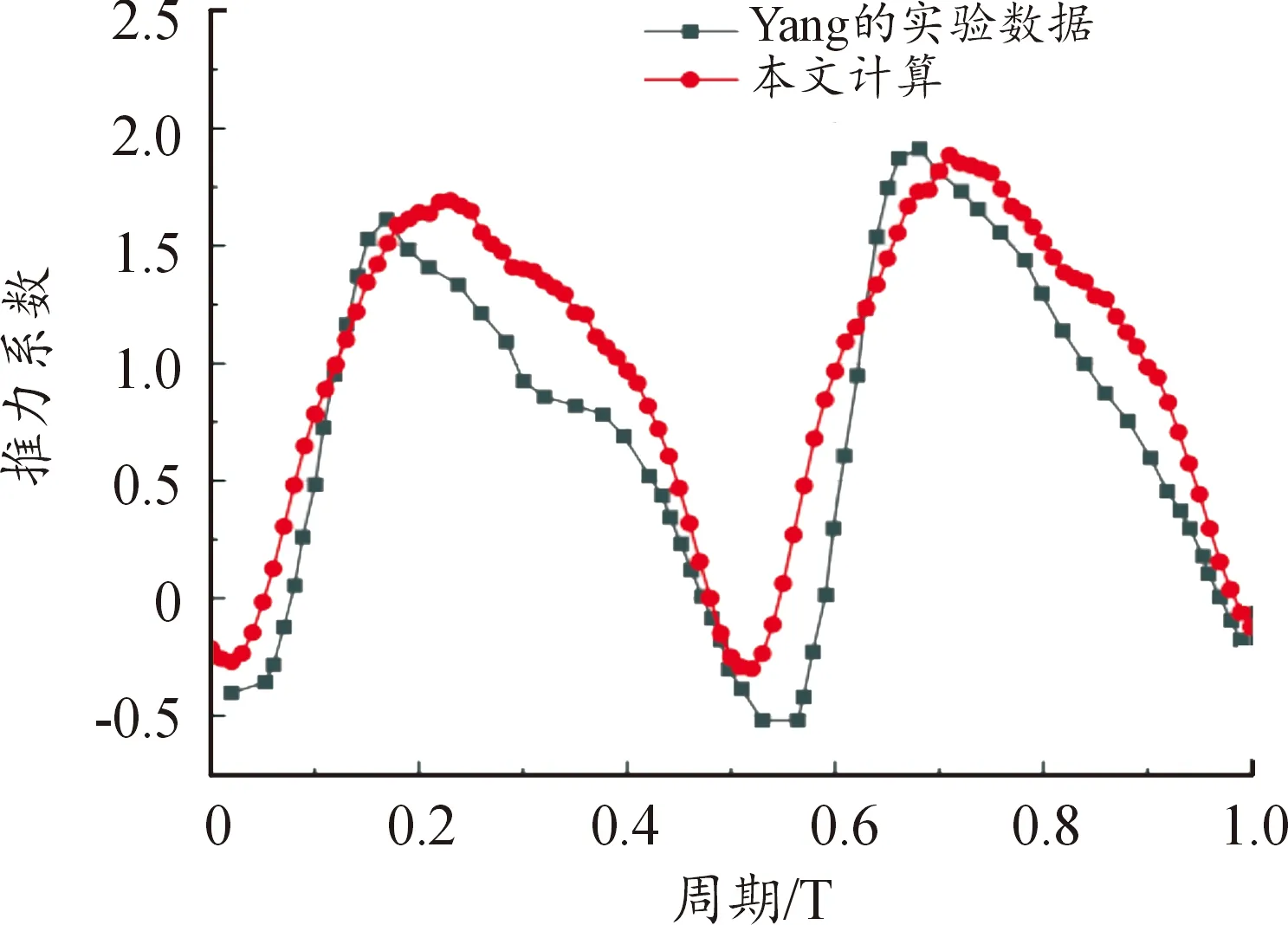
图4 本文的气动力方法与Yang实验数据对比

从图4中可以看出，本文采用的气动力计算方法计算结果与实验数据吻合效果较好，部分数据存在波动，这是因为Yang等人的扑翼模型数据是利用DIC技术采集得到，而本文的扑翼计算模型是根据Yang等人的扑翼几何参数所建立，导致本文的扑翼模型在翼面后缘部分与实验模型有微小差别，引起了小幅度的波动。总体来看，本文的仿真计算结果符合真实样机的气动力实验结果，这说明本文的扑翼气动力计算方法准确性较高。可以准确计算扑翼的气动性能。

3 数值结果与分析

本文主要研究扭转运动和水平运动对扑翼升力方向(Z)与推力方向(X)的气动性能影响，研究在不同扑动频率以及不同自由度下扑翼的气动性能和流场结构。

3.1 不同自由度对气动性能的影响

基于图1的扑翼模型，本文将扑翼扑动运动起始行程定义为由下扑行程起点向下扑动，扑翼的扭转运动起始行程为向下扭转，扑翼的水平运动起始行程定义为向后(-X)运动，扑动运动与扭转运动的频率一致，即上扑行程时，扑翼向上扑动，翼面向上扭转，扑翼也同时向前运动，而下扑行程时，扑翼向下扑动，翼面向下扭转，扑翼同时向后运动。扑翼水平运动的频率调控参数k取值为1，对不同自由度的升力和推力系数进行了数值计算，得到扑翼在一个周期内不同自由度下的升力和推力系数变化曲线如图5和图6所示。

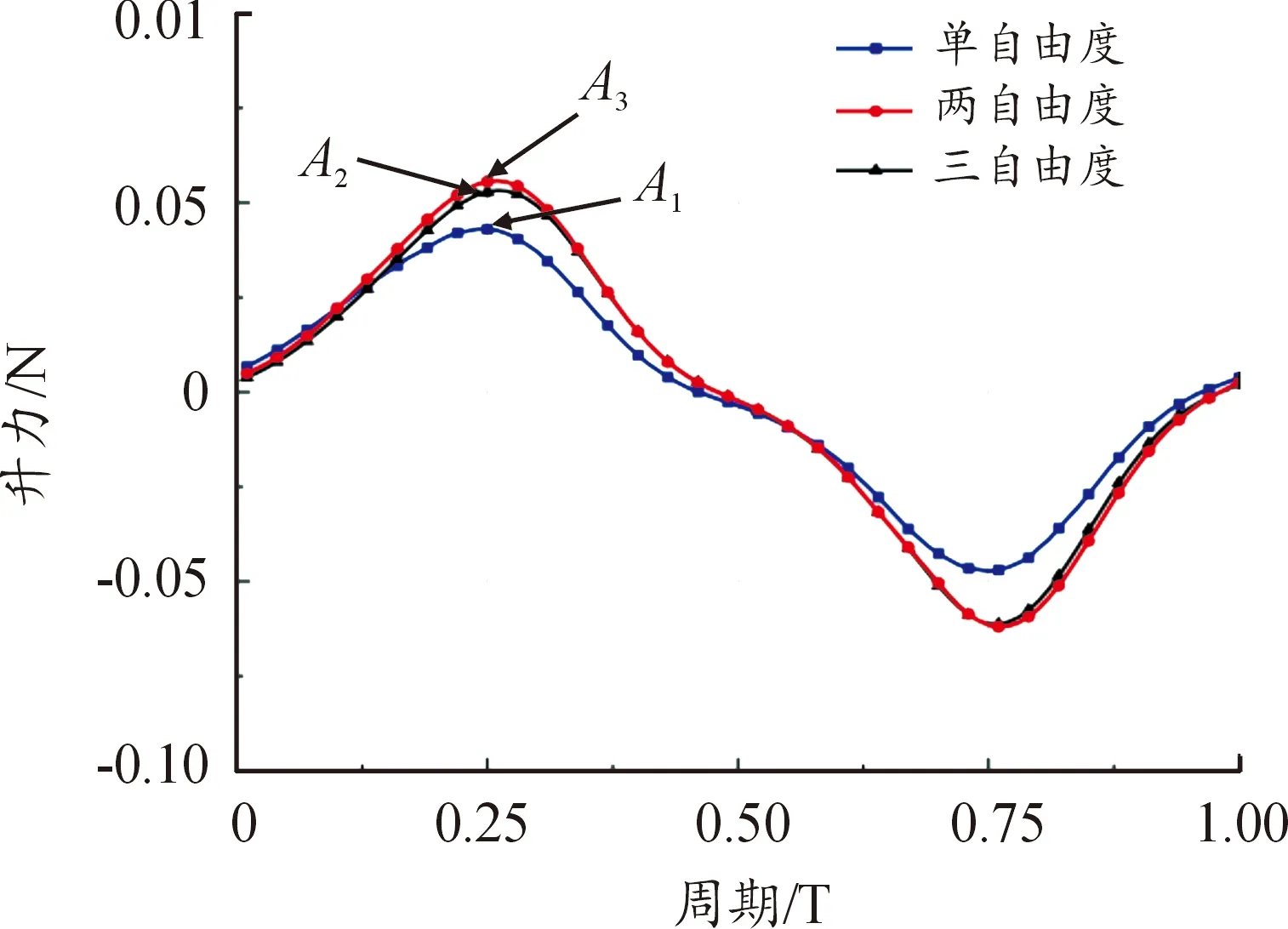
图5 不同自由度的升力变化曲线

其中0T-0.5T为下扑行程，0.5T-1T为上扑行程。从图5中可以看出，当加入扭转运动后，两自由度的升力峰值A2相比单自由度升力峰值A1提升了28%，而3自由度与两自由度相比，两者的升力变化曲线几乎重合，这说明扑翼的扭转运动可有效提升扑翼升力性能，而水平运动对升力的产生几乎没有影响。

在推力性能方面，如图6所示，在单自由度扑动时，扑翼在整个扑动行程中推力系数都处于正值，扑翼的推力系数峰值B1都出现在下扑行程的水平位置，即图5中的A1时刻；而3自由度下的扑翼在下扑行程时，推力系数为正，在上扑行程时出现较小负推力系数。推力峰值B3和两自由度B2较单自由度B1而言提前了0.12T，即出现在扑翼下扑至水平位置之前。

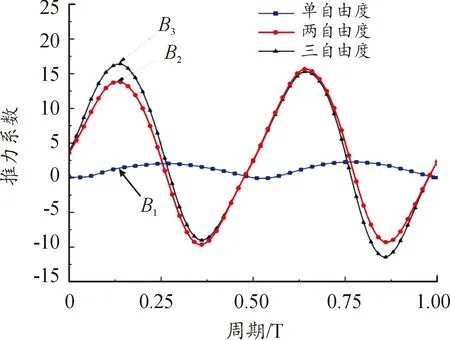
图6 扑动频率为5 Hz下不同自由度的推力系数曲线

相对于单自由度扑翼的下扑行程，加入弦向扭转运动后，随着扑翼向下扭转的角度逐渐增加，在B2时刻(0.12T)推力系数增大到峰值，与该时刻单自由度的推力系数B1相比，扑翼的推力性能大幅度提升了4.69倍。在两自由度扑翼的基础上加入水平运动后，即3自由度下的推力峰值B3得到了更进一步的提升，与B1相比，具备3个自由度的扑翼推力系数提升了6.26倍，显著提高了扑翼的推力性能。

3.2 不同扑动频率对气动性能的影响

在扑翼运动中，机翼的扑动频率也是影响升力和推力性能大小的重要因素，较大频率的运动不仅改变了扑翼附近的流场速度，同时还改变了扑翼表面的气压，从而改变气流在整个翼展的分布情况。因此，本文还研究了扑翼在3自由度下不同扑动频率的气动特性。与上文的计算方法一致，本文计算了扑动频率为10 Hz下的气动性能，得到了不同扑动频率下扑翼的升力和推力系数变化曲线如图7和图8所示。

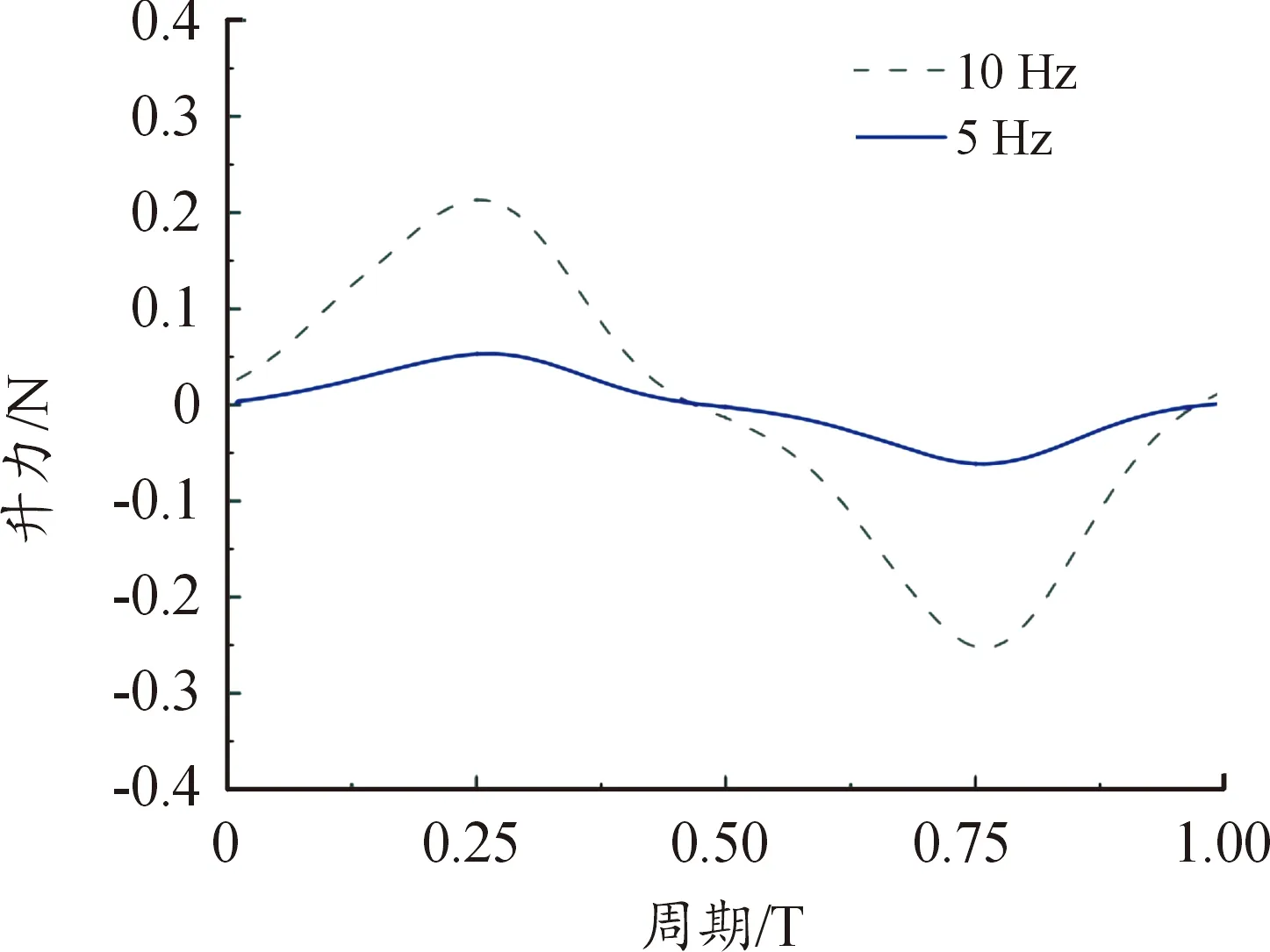
图7 3自由度下10 Hz和5 Hz的升力变化曲线

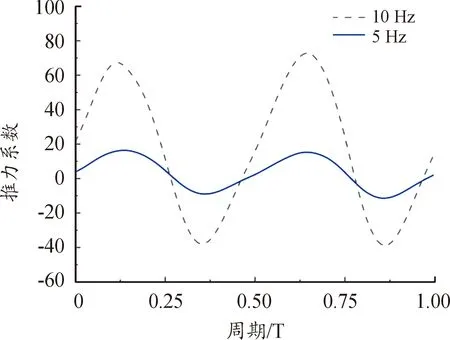
图8 3自由度下10 Hz和5 Hz的推力系数变化曲线

从图7中可以看出，扑动频率为10 Hz时最大升力为0.224 N，5 Hz下最大升力为0.055 1 N，相比之下，在3自由度扑动模式下，扑动频率10 Hz下升力比5 Hz提高了3倍。

在推力性能方面，从图8中可以看出，10 Hz下最大推力系数为78，10 Hz和5 Hz的推力峰值都出现在上扑行程结束后开始下扑行程的起始位置附近。扑动频率5 Hz与10 Hz相比，10 Hz下扑翼的推力提高了4.26倍，且在上扑行程起始位置附近的推力提升更大。

3.3 不同运动频率对气动性能的影响分析

为了进一步探索扑动模式对扑翼气动性能的影响的力学，本文继续研究了扑翼相对运动频率对气动性能的影响。在水平前飞工况下的3自由度扑翼基础上，对水平挥摆运动引入了运动频率调控参数k，分别计算了当k=1、2和3时的气动力参数，得到3自由度下不同运动频率的升力和推力系数变化曲线如图9和图10所示。从图9中可以看出，在下扑行程中，相对于k=1的常规3自由度运动而言，当k=2时，扑翼的升力峰值增加了6%，随着水平运动频率增大，当k=3时，扑翼的升力峰值减小了4%，而在上扑行程中，扑翼的负升力峰值随着水平运动频率的增大逐渐增大，当k=2时，扑翼的负升力峰值增大了3.6%，当k=3时，扑翼的负升力峰值增大了6%。

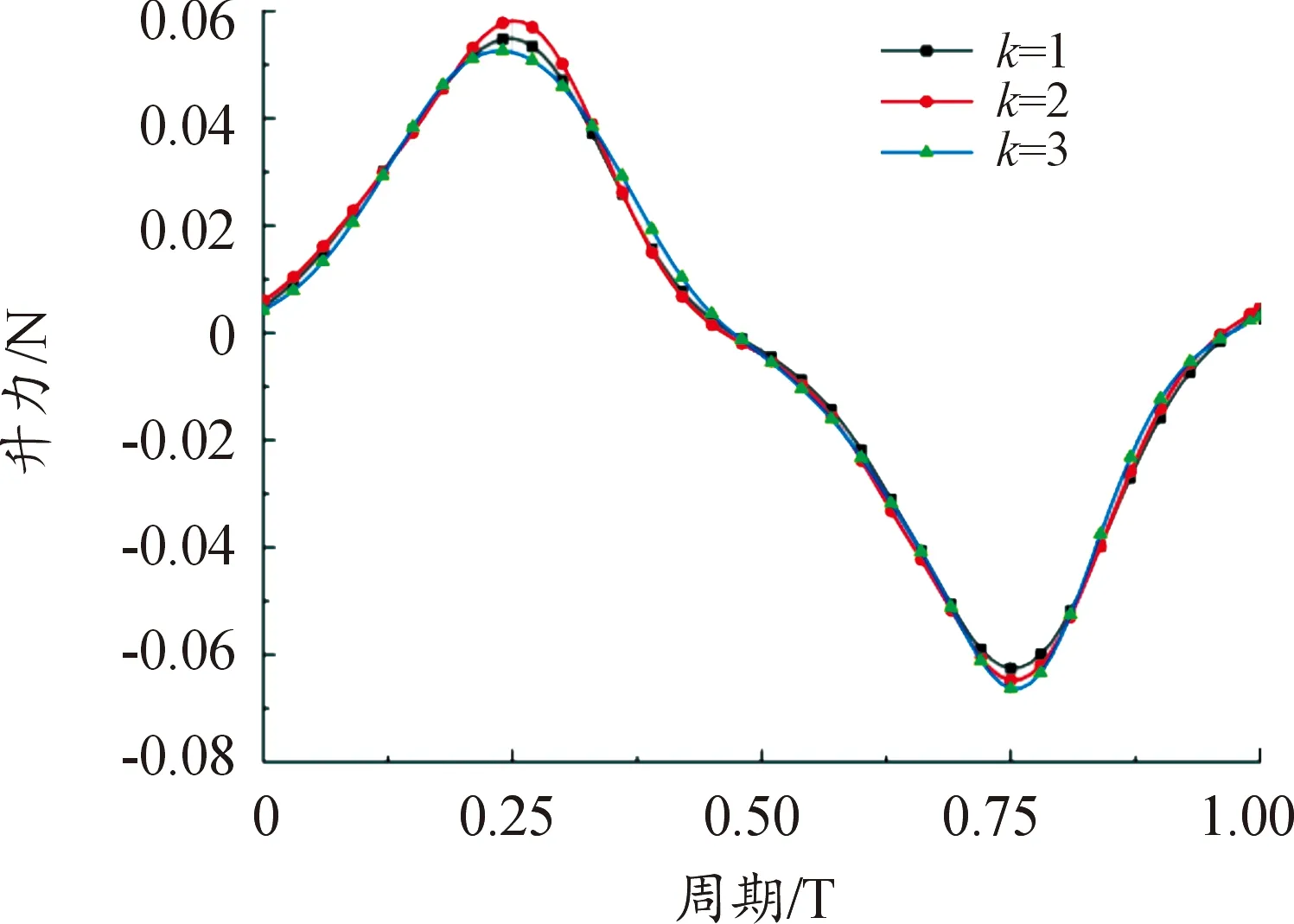
图9 3自由度下不同水平运动频率的升力变化曲线

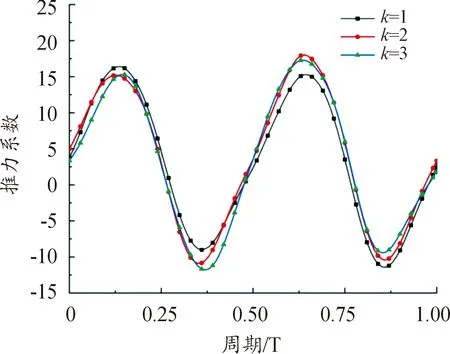
图10 3自由度下不同运动频率的推力系数变化曲线

在推力性能方面，在下扑行程中，扑翼的推力系数随着k值的增加略有降低，而相对于k=1而言，k=2和k=3的推力峰值接近，推力峰值均降低了7%；在上扑行程中，随着水平运动频率的增大，扑翼的推力系数逐渐增加，当k=2时，扑翼的推力系数峰值增加了17.8%，当k=3时，扑翼的推力系数峰值增加了13%。

综合来看，加入扭转运动会使扑翼的升力小幅度增加，推力性能大幅度增加；而再加入水平运动即3自由度运动后，进一步提升了扑翼的推力性能。随着扑动频率的增加，扑翼3自由度运动模式的升力性能和推力性能得到了更大幅度的提升，这表明扑动频率对扑翼的气动性能具有正相关的显著影响。此外，随着扑翼的水平运动频率增加，扑翼的升力略有提高，但同时也会增加负升力，而在推力性能方面，水平运动频率的增大会小幅度减小扑翼下扑行程的气动推力性能，但会显著提高扑翼在上扑行程的气动推力性能。

4 气动机理分析

为了详细阐述3自由度下扑翼的气动机理，本文将不同自由度的数据计算结果导入CFD-POST软件进行后处理，截取了一个完整扑动周期的计算结果，通过扑翼展向压力场分布情况和涡结构变化过程对不同自由度的气动特性进行分析。

4.1 扑翼压力场分析

通过对数值计算结果的处理，得到扑翼YZ截面0.12c处不同拍动行程压力云图如图11所示。

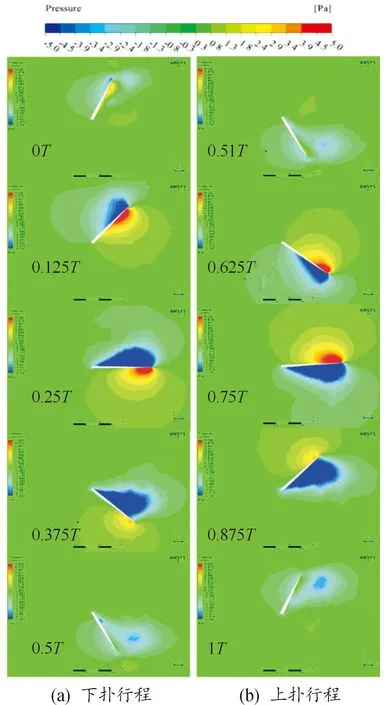
图11 扑翼YZ截面不同拍动行程压力云图

4.2 扑翼涡结构分析

为了进一步揭示不同自由度下扑翼气动力的产生机理，本文还将A时刻升力峰值和B时刻推力峰值的涡结构进行了提取，得到了图12扑翼弦向0.4R处截面涡量云图。在A时刻，从图12可以看出，当扑翼下扑到水平位置时，在扑翼上表面产生了强烈前缘涡，前缘涡具有附着于扑翼表面不脱落的特性，附着于翼面的前缘涡面积越大，扑翼的翼面压差也就越大，这也解释了图11中该时刻(0.5T)的翼面压差达到最大，由此产生升力峰值的原因。此外，当添加扭转运动后，扑翼上表面的前缘涡明显变得更强，涡形也变得更加饱满，而加入水平运动后，A3相对于与A2的前缘涡强度和范围变化不大。

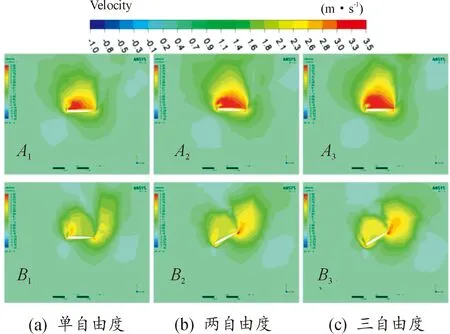
图12 扑翼弦向0.4R截面涡量云图

当扑翼在上下扑动的转换阶段，会在扑翼的后缘产生一个尾缘涡随着空气的流动向后脱落，受到尾缘涡的诱导作用，在扑翼后缘附近将产生一个与来流相同方向的流动区域，此时漩涡中各处的诱导速度与来流方向相同，扑翼会受到推力。反之，当漩涡中各处的诱导速度与来流方向相反时，扑翼会受到阻力。

对于B时刻的涡量云图，通过对比图12(a)、(b)和(c)可知，在单自由度扑翼B1时刻，机翼后缘处行成了尾缘涡，准备开始脱落行程，而在多自由度扑翼的B2和B3时刻，扑翼下表面的尾缘涡已完全脱落，且3自由度扑翼脱落的尾缘涡的形状要比两自由度更大，涡的强度也明显强于前者。

综上所述，通过比较升力和推力系数曲线，可以发现扑翼的扭转运动会扩大前缘涡的形状和增大前缘涡的强度，从而提高扑翼的升力性能。此外，扭转运动还会加快扑翼下表面尾缘涡的脱落速度，使得多自由度扑翼提前达到推力峰值，且脱落的尾缘涡形状更大，强度更大，这也是扑翼的推力性能得到大幅度提升的主要原因；而水平运动对前缘涡的形成几乎没有影响，但是扑翼加入水平运动使得扑翼脱落的尾缘涡强度获得小幅度提升，形状变大，致使3自由度扑翼的推力性能得到了进一步提升。

5 结论

针对扭转和水平挥摆运动对三维扑动模型的气动性能问题，基于FLUENT建立了三维扑翼气动力仿真模型，计算了不同自由度和不同频率下的升力、推力性能，并结合一个周期内不同扑动行程的压力云图和涡结构变化揭示了运动模式对三维扑翼气动性能影响。研究表明：

1)本文建立的三维扑翼气动力计算模型和计算方法与实验测试结果吻合度较高，可准确计算扑翼的气动性能。

2)与单自由度扑翼相比，在迎风水平前飞时，扑翼加入弦向扭转运动(两自由度)使扑翼的升力提升了25%，推力性能提升了4.69倍；而加入水平挥摆运动(3自由度)对扑翼的升力性能影响微小，但是使推力性能提升了6.26倍，且在不同的扑动频率下，多自由度运动对扑翼气动性能的提升效果更加明显。

3)相对于常规3自由度扑翼运动而言，水平运动频率调控参数k对扑翼气动性能的影响比较明显，随着水平运动频率的增加，扑翼的气动升力先增大后减小，在下扑行程中，随着k值的增大，扑翼的推力性能逐渐减小，而在上扑行程中，扑翼的推力性能先后增大后减小。当k=2时，扑翼的升力峰值增加了6%，扑翼的推力系数峰值增加了17.8%，为取得较好的气动性能，k=2的3自由度扑翼是一个比较好的选择。

4)扑翼的弦向扭转运动加速了扑翼下表面的前缘涡脱落进程，改变了前缘涡的脱落强度和形状，增大了扑翼后缘与来流相同方向的流动区域强度，从而提高了推力性能；而水平挥摆运动会使两自由度扑翼下表面脱落的尾缘涡强度得到进一步提高，脱落的尾缘涡形状更大，从而使扑翼获得更佳的气动性能。