基于“数学+”的线性代数课程深度学习研究

姚 斌，杨红伟，杨玲香

（石河子大学 理学院，新疆 石河子 832003）

深度学习最早由Marton等人提出，他们将学习者的学习分为浅层学习和深度学习。Marton认为深度学习是指学习者在理解学科知识的基础上，对新学习的学科知识和思想方法进行批判性的学习与融合，并将其融入自身已有知识和经验结构中，最终能够运用迁移知识解决实际问题［1］。李沁等基于课堂深度学习实践困境的剖析，探寻并思考课堂深度学习的实践路径［2］。唐玉溪从深度学习理论出发，系统梳理学界相关认知神经科学研究成果，挖掘深度学习活动背后的认知神经机制，以期对教学实践有一定的启发作用［3］。马如霞等以课堂师生对话行为作为研究对象，通过实证研究聚焦当前课堂深度学习的现状，探究促进课堂深度学习的策略［4］。

一、线性代数教学现状

线性代数课程是大学数学公共基础课之一。本课程概念、公式、定理较多，且内容纵横交错，前后联系紧密，环环相扣，相互渗透，计算相对复杂但规律性强，解题方法灵活多变，对学生的抽象思维能力与逻辑推理性有较高的要求。学生在学习过程中普遍感到课程内容过于抽象，学习兴趣随着课程的深入越来越低，学后对很多知识点的掌握都流于表面，只知其行，不知其意，不懂如何运用它们解决实际问题，只会模仿例题机械式的解题，课程的获得感不高。

在以往的线性代数教学中，课程重点讲授的是概念、定理及计算，注重的是知识逻辑的严密性和计算的准确率。随着时代的发展，不少高校在课程教学中融入数学软件Matlab，引导学生运用数学软件计算相关问题。但通过学生座谈及问卷调查等显示，学生对所学知识具体是如何抽象出来的，到底有什么用以及怎么用还是存在诸多困惑。学生主动参与课堂的意愿较低。究其原因，主要是课程教学中重点关注的是代数方法以及计算过程的准确性和简洁性，而忽略了课程所体现的几何观念和解决问题的思维产生过程。课程考核重点关注的是学生的计算水平，也就是布鲁姆目标分类理论的浅层次水平。学生很难自主构建所学知识与现实生活的联系，导致学生很难学以致用，难以用数学的语言描述问题，进而解决问题。

二、基于“数学+”的深度学习培养策略

（一）数学+创新思维方法：优化课程教学内容，将创新思维方法融入线性代数课堂教学

当今社会对大学生的创新能力提出了更高的要求。“四新”建设的“新”不是新旧的新，是创新的新，是整个发展思路、标准、路径、技术方法和评价等系列的新变化［5］。教师应结合时代需求及课程特点进行教学设计，深入研究课程的哪些知识点能够与创新思维方法相融合。在线性代数课程教学中，着重将形象思维、逆向思维、发散思维、类比思维和批判性思维等创新思维方法融入课堂教学。结合具体的教学内容，设计教学目标，提炼相应的科学思维方法，总结学习经验，设计教学方式，让学生明白思维的产生和运用过程。

第一，在线性代数教学中，重视思辨数学的教育价值，设计数形结合，几何直观案例，让学生体验形象思维的运用和价值。例如，以往在讲解向量的夹角时，直接给出夹角公式学生能够运用该公式计算夹角，却无法理解公式的来源。教学过程中，教师可以从几何直观入手，建立三维空间直角坐标系，让学生直观感受如何由内积推导得出向量夹角公式，进一步推广到任意向量的情形。

第二，通过不同知识点之间的对比和细分，带领学生对其进行深度解读，发现它们的区别和联系，培养学生的类比思维和发散思维。例如，在讲解向量的线性组合时，可以从同学们熟悉的三原色原理出发，人的眼睛对红、绿、蓝最为敏感，它像一个三色接收器的体系，大多数的颜色可以通过红、绿、蓝三色按照不同的比例合成产生。同样，绝大多数单色光也可以分解成红、绿、蓝三种色光，这是色度学的基本的原理，也称三原色原理［6］。是否能用数学的语言来描述这一现象呢？将颜色类比成向量，则三原色原理可以表示为：

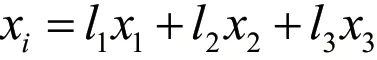
其中，x1,x2,x3分别表示红绿蓝三种颜色，xi代表任意一种颜色，123,,lll表示比例。

即任意一种颜色可以表示成红绿蓝三种颜色的比例组合。这一问题是否可以推广呢？进一步通过类比引出向量的线性组合的概念。

定义：给定向量β和向量组α1,α2,… ,αn，如果存在一组数k1,k2, …,kn使得

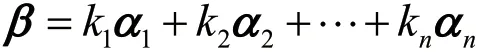
则称向量β为向量组α1,α2, …,αn的一个线性组合，或者说β可由向量组α1,α2, …,αn线性表示，k1,k2, …,kn称为组合系数［6］。

第三，在习题课的教学中，精心设计相关习题，尝试从一题多解、逆向思考、题目变式训练等多个方面培养学生的逆向思维、批判性思维和发散思维。具体要注重题目选择的层次性，逐步递进，通过类似思维训练，有效地培养学生的发散思维，开阔学生思路。

（二）数学+实际问题解决：基于实际问题解决的线性代数深度学习任务设计

当前，混合式教学打破了时空界限，拓展了教学空间，成了广受欢迎的一种教学形式。在教学过程中，依托前期建设的线性代数课程混合式教学资源，构建了课程混合式教学环境，满足学生个性化学习的需要。同时，在上述思维教学基础上，进一步优化了内容。结合“传递—接受”和“自主—探究”两种模式之所长，聚焦线性代数在新一代信息技术、智能制造、经济学等领域的广泛应用，围绕学习内容设置具有开放性、发散性和探究性等特征的实际问题，让学生组建学习小组，从不同角度思考和探究运用所学知识解决现实问题，从而让学习活动实践化，为调动已有知识与创造新的知识提供可能与基础［7］。

具体实施过程如下：以“矩阵的初等变换”为例

教师引导：学生课前完成在线预习任务，教师在课堂上进一步讲解初等变换的理论知识，主要结论。帮助学生掌握核心学科知识，进行相关知识储备，为开展深度学习打下基础。

深度学习任务设计：教师布置线上学习任务——“小组合照图像旋转的数学机理探究”。具体包含如下内容：一是正向问题。以小组合照图像为例，如何利用初等变换实现该图像任意角度的旋转？二是反向发散问题。已知一幅旋转后的图像，能否运用所学知识推断原图像，并给出旋转角度。三是拓展问题。请在此基础上提出一个新问题，并思考解决方案。

小组任务解决：小组成员依据任务查找相关资料进行个体的知识建构并共享观点及相关支撑材料，通过沟通，质疑和协商后达成共识，最终完成相关任务。通过该任务帮助学生真正理解学习内容，应用形象思维、逆向思维和发散思维等解决实际问题。学生也将在共同的协作中锻炼复杂问题解决能力，沟通能力和团队协作能力。

汇报交流：各小组通过汇报交流学习成果，其他小组提出相关问题或质疑。教师提出疑问，引发学生思考和交流，培养批判性思维，提升自学能力。

上述任务贴近学生实际生活。难度稍高于学生的实际知识掌握水平。学生可在教师的指导和帮助下以及与小组的协作中解决。目前，智能手机都装有图像处理APP，学生大都能够熟练使用这类APP处理各种照片，但很少去探究这些操作都是怎么实现的？这就是所谓的“黑盒子”理论，使用者的门槛很低，研发的门槛越来越高。这背后蕴含了大量的数学过程。

三、教学实践与分析

本研究以S大学连续两届线性代数教学班学生为研究对象，进行了两轮的教学研究实践，具体实施情况如下。

（一）第一轮教学实践

2021年，第一轮主要包括课前自学，课中讲解汇报，课后讨论测试等。教师课前通过网络教学平台发布自主学习任务单，学生通过阅读自主学习任务单，明确课前学习任务，包括预习视频、书本知识点、在线讨论题及课前阅读材料等。由于数学课程难度较大，完全由学生课前自学，大部分学生会比较吃力。所以课前预习主要涉及课程中相对简单的知识点的概念及基本计算。课中教师会针对重要内容进行讲解、思维训练及实际问题解决案例分析。课后主要是完成作业、小组合作任务、讨论及测试等。

在第一轮的教学实践中，教师共发布在线讨论题63道，讨论题的设计重点关注学生思维层次的训练，以期让学生在课后更深层次理解教师所讲授的内容。为了达到以测代练的目的，课后测试允许学生重复3次。小组合作任务共5道。

第一轮教学实践完成后，教师通过面对面访谈和调查问卷等方式，了解学生学习感受。学生普遍反映可以接受教师采取的教学方式，但也提出了一些问题。一是自主学习任务较多，部分学生自主学习预习视频的积极性不高。二是在线讨论题过多，虽然教师只要求同学自主选择自己感兴趣的参加讨论即可，但不少学生为了获得高分，基本所有讨论题都参与，导致讨论题灌水现象严重。三是在线测试反馈不及时。每章学习完后才开始在线测试，学生又要学习新一章的内容，基本无暇顾及上一章的知识点巩固。四是小组任务设计题目偏难，部分学生查阅资料也无法有效完成。

（二）第二轮教学实践

针对上述问题，教师之间进行了交流讨论，对混合式教学策略进行了一定调整。一是根据学生反馈，对自主学习任务单中相对较难的知识点调整为课内教学。二是对在线讨论题进行了适度删减，每章在线讨论题不超过5道。三是课中教学使用雨课堂进行，每节课中发布1—2道测试题，便于教师及时了解学生掌握情况，调整教学进度。四是小组合作任务题目减少到3道，并根据学生学情调整了部分任务难度，增加了部分任务解决思路的提示。

教师根据上述调整进行了第二轮教学实践。教学实践完成后教师再次对学生进行了访谈和问卷调查，学生对教师采取的教学策略满意度明显提升。同时，在实际问题解决部分，学生普遍感觉还是偏难。由于本课程面向大一学生，学生专业知识储备较少，所以实际问题解决对学生的挑战较大。后期教师将在这部分的讲解和反馈上加大力度。

四、建议

第一，教师要深入学习创新思维的内涵，精心设计思维训练方式，拓展内容的深度和广度。注重发掘创新思维与数学理论之间的关联，如新概念能不能直接从旧概念或者实际生活中的某些“通识性原理”引入；抽象的代数概念能不能从几何的角度直观引入；新概念引入后能不能更加“简洁方便”地得到某些已有的数学理论；一题多解的各种解法各有什么优缺点；同一种方法解不同类型问题的原理和过程是否相同等方面入手，不断拓展相关案例。可以尝试布置习题变式等作业，让学生自主探究相关题目的演变、拓展及延伸，以期达到思维能力的跃升。

第二，在具体实施时，要注重课程教学设计。教学改革的成败一定程度上依赖于教师的教学设计。教学材料的选择要时刻关注学科的最新发展态势，动态更新相关教学内容。同时，教学设计要紧跟时代步伐，融入现代教育教学理论与工具，不仅注重教师的教，还要研究学生的学，关注学生易于接受的教学方式及学习方式，通过有效的教学导引让学生深度参与教学的各个环节。

第三，深度学习任务的设计要能够匹配学生的实际水平。不同高校的学情不同，教师在设计相关任务时，首先要考虑任务与学生实际情况的契合度，解决任务需要的数学原理和背景知识是否匹配课程的内容和学生的认知水平；其次要考虑任务的可达性，任务是否难度适宜。小组合作任务的设计问题不能太大，要略高于学生现有的能力，但不能遥不可及。这就要求教师要对任务进行拆解，使其变成学生跳一跳就能够做的事情；同时还要考虑任务的实用性，任务是否来源于实际生活或其他学科中的实际问题，使学生能够在任务解决中自主实现知识的迁移应用，达到深度学习的目的。

五、结语

综上所述，在线性代数教学中开展深度学习改革研究，拓展了教学时空，对学生关于课程知识的理解和计算有着一定促进作用。各类教学环节涉及内容广泛，有效地拓展了学生的发散思维、逆向思维和批判性思维等，学生应用数学意识得到明显增强，且学生对课程的获得感也有所增强。在后续教学中，教师仍需不断探索，优化教学策略。