基于混合A*算法的自动驾驶汽车轨迹生成

周苏 王若伊 张友发 张岗

（1.同济大学汽车学院，上海 201804；2.同济大学中德学院，上海 201804）

主题词：混合A*算法 轨迹优化算法 贝塞尔曲线 自动驾驶

1 引言

自动驾驶汽车配备先进的传感器、控制器和执行器，可以感知复杂环境、进行智能决策和运动控制，最终使车辆达到人类驾驶员驾驶水平[1-2]。

规划作为驾驶自动化系统中不可缺少的环节[3]，不仅需要从感知层获取当前的周围环境信息和自身定位信息，还需要将规划好的动作信息传到控制层，再交由控制层对汽车进行控制。一个规划迅速、反应良好的规划层直接影响无人驾驶汽车的性能。

20世纪至今，规划方法发展迅速，根据具体的计算方法，规划算法分为5类：

（1）基于图搜索的规划算法；

（2）基于采样的规划算法；

（3）基于插值的规划算法；

（4）基于数值优化的规划算法；

（5）基于机器学习的规划算法。

各类规划算法研究进展如下：

（1）基于图搜索的规划算法

图搜索算法主要指遍历从起点到终点的状态空间以搜索出当前最优的结果，一般使用栅格、格子来表示一个点的状态。

迪杰斯特拉算法是1种单源最短路径的最优路径规划算法，在迪杰斯特拉算法中配置状态空间，一般被离散为单元网格后再进行搜索[4]。Dijkstra最早给出了这种算法的严格证明[5]。在自动驾驶领域，迪杰斯特拉算法已经被应用于多车仿真中[6]，本-富兰克林车队（The Ben Franklin Racing Team）和维克多-探戈（Vector Tango）将其应用于DARPA城市挑战赛中[7]。

A*算法是带有启发式函数的迪杰斯特拉算法，非常适合已知地图下的路径规划问题[8]，但是当要搜索的区域过大时，其所耗费的内存空间也会随之增大，搜索速度随之下降。

A*类算法家族具有很多成员，这些A*类算法相比A*有了很多的提升，也被广泛应用到自动驾驶、机器人等领域。比较常见的有Hybrid A*算法、D*算法（Dynamic A*,D*）、Field A*算法[9]、Theta*算法[10]、ARA*算法（Anytime Reparing A*,ARA*）和AD*算法（Anytime D*,AD*）[11]。在自动驾驶领域中，Ziegler等[12]在文献中实现了A*算法用于非结构化空间下（停车场）的规划。混合状态A*算法被斯坦福大学用于DARPA挑战赛[13]。2007年的DARPA挑战赛获胜车辆Boss也使用了AD*算法[14]。Saeid等[15]使用了Hybrid A*算法实现了停车场中实验车辆的自动泊车。Francesco等[16]则通过减少车辆转弯和向后行驶，提高了乘客在自动泊车时的乘坐舒适度。Silvana等[17]使用正态分布变换算法建图后，使用Hybrid A*算法进行路径规划，并使用模型预测控制算法进行控制器设计，实现了在园区内稳定运行的高尔夫球车。

Howard等[18]将状态栅格法应用于崎岖地形下的轮式移动机器人的全局规划和局部规划。Likhachev等[8]根据控制复杂度将状态空间离散化，而McNaughton等[19-22]考虑了时间和速度，将状态根据时间空间离散化。

（2）基于采样的规划算法

基于采样的算法中也有很多实用且高效的算法。如概率路图法（Probabilistic Roadmap,PRM）[23]，快速搜索随机树算法（Rapidly-Exploring Random Trees,RRT）[24]。其中，RRT算法也已经被应用到自动驾驶领域。

RRT算法是一种快速的在线搜索算法[25]，可以在半结构化空间中进行快速规划，考虑了非完整约束[24]。MIT将该算法应用到了DARPA挑战赛中[26]，但其结果并不稳定，而且曲率也不连续。与A*类算法一致，RRT类算法也有很多成员，如RRT*算法[27]、Informed RRT*算法[28]、Anytime RRT*算法[29]，以及Kino-Dynamic RRT*算法[29]。

（3）基于插值的规划算法

Reeds等[31-32]使用了直线和圆弧插值算法来近似汽车规划。螺旋曲线插值中对应的曲线是根据菲涅尔积分定义而来的[33]，使用回旋曲线可以定义曲率线性变化的轨迹，平滑过渡直线段和弯曲线段[34]。多项式插值算法非常适合多段轨迹的插值问题。Piazzi等在文献[35]、[36]和[37]中分别阐述了相关的计算方法。贝塞尔曲线插值广泛应用于航空航天、汽车设计、游戏众多领域，在自动驾驶领域的研究中，三阶和四阶的贝塞尔曲线被用来规划当前可以转弯、避障的轨迹[38-39]。

（4）基于数值优化的规划算法

基于数值优化[40-41]的方法时间上是使受不同约束的函数最大化或者最小化，大多数是基于凸优化的算法，还有一些是基于非线性优化的算法。这种算法实际上已经被广泛应用于移动机器人在狭窄通道中避障的势场方法（Potential Field Method,PFM），其轨迹可以包含一阶连续性[42]甚至更高阶（速度、加速度、冲击度等）连续性的轨迹。

（5）基于机器学习的规划算法

基于机器学习的方法具有较快的计算速度和较强的泛化能力，但是使用机器学习的方法之前需要进行一定的离线学习。以下机器学习相关的方法被应用在规划领域：强化学习[43]、流形学习[44]、卷积神经网络[45]、隐马尔可夫模型[46]、高斯混合模型[47]和径向基函数神经网络[48]。

通过以上分析，目前自动驾驶车辆的运动规划算法存在以下缺陷：

（1）考虑了汽车动力学的规划算法计算较慢，且不能保证规划处的路径总是无碰撞的。

（2）汽车的路径规划与某些机器人和无人机的路径规划不同，汽车的运动规划属于非完整约束问题，且大多数规划算法规划出的结果是路径，并没有规划出其轨迹。而且即便是有轨迹规划的算法，其路径和速度是不匹配的，需要对速度重新进行规划。

（3）大多数规划算法并没有考虑多车协同问题。现在绝大多数的规划算法都是考虑已知地图下的单车规划问题。

因此，本文以提高汽车舒适性为目的，基于汽车的最小冲击度进行建模，在MATLAB和栅格地图中进行了算法预研，解决了自动驾驶汽车运动过程中舒适度不足的问题。然后，针对优化算法可能导致轨迹碰撞的问题，对优化算法进行了改进，保证了汽车的安全性，并给出了“走廊”自动调整的策略。

2 基于混合状态A*算法的路径规划模型

混合状态A*算法最早出现于2007年美国DRAPA挑战赛[49]，它并不像迪杰斯特拉算法、A*算法那样经过数学推导而得出，但这并不影响该算法的实用性。2007年，斯坦福大学的车队就是使用该算法跑完了全程。混合A*算法是A*算法的一种变体，它不仅继承了A*算法的特性，还可以在更高维度的状态空间进行搜索，并提出新的状态更新规则。

相比A*算法，混合状态A*算法具有更高的搜索维度，主要体现在以下方面：

（1）一般混合状态A*算法会在x坐标、y坐标、朝向角和转弯半径4个维度进行路径规划。而A*算法会选取当前累计代价和启发式函数代价最小的点作为下一点来膨胀；

（2）与此类似，混合状态A*算法则是基于A*算法和Reeds_Shepp曲线[31]来决定下一节点，其节点可以不是栅格的顶点。

图1是混合状态A*算法的流程图。

图1 混合状态A*算法流程

3 基于最小冲击度的优化模型

由于很多路径规划算法会将汽车视为点来进行路径规划，这导致某些规划算法规划出的路径超出了汽车的正常行驶范围，且不能保证车内乘客的舒适性。为了提高汽车在运动过程中的舒适性，本文将对混合A*算法的结果基于最小冲击度进行优化。

3.1 基于最小冲击度的一维优化模型的建立

本文建立的基于最小冲击度的优化模型，取最小冲击度的L2范数的平方作为优化的目标函数，优化目标是最小化最小冲击度的平方，目标函数如式（1）所示。

式中，Jk为目标函数；T为优化模型时间域；jk为最小冲击度。

选取当前的状态量为

式中，sk为当前的状态量；pk当前状态的位置；vk是当前的速度；ak是当前的加速度。同时，将外界输入定义为：

整个系统的状态表达为：

式中，fs(sk,uk)为当前状态量与外界输入的状态表达式。结合庞特里亚金极大值（极小值）原理，可得最终的状态表达式[50]：

式中，s*(t)为系统的最优状态表达式；t为时间；α、β、γ为任意常数；α0、a0、v0、p0为t=0时的系数、加速度、速度和位置。

3.2 多段优化模型边值问题求解

对于轨迹规划问题，工程中很难只用一段多项表达式就拟合出一个符合预期的从起点到终点的轨迹，更一般性的做法是用多段连续的多项表达式拟合。本文中，后续出现的多项式连续条件均指位置连续、速度连续和加速度连续。同时，路径的多项表达式还需要满足运动的初始条件和终止条件。

对于多项表达式，可以用如下表达式来表示：

式中，f(t)为多段连续多项式的总表达式；fM(t)为各段多项式表达式；TM-1≤t≤TM为时间分段。

同时还需满足如下约束：

式（7）是指多项表达式中每相邻2段表达式之间连接处需要满足连续性约束；而式（8）是指第j段表达式的头和尾部需要满足该处的状态约束（位置、速度以及加速度）。本文中，每相邻2段的状态约束只包含位置约束。

有了以上目标函数和约束还不够，为了求解多段表达式的最小冲击度，还需要知道每段上的时间。本文中的时间按照常数或者梯形速度曲线进行分配。

综上可以得出最终优化表达式：

式中，min式为凸目标函数；s.t.式为约束函数；Ti为仿射函数。

3.3 基于最小冲击度的优化结果

在以下场景中，设置汽车起始位置为[9,16,0]，再绕过障碍物后，需要停在停车位上，最终的状态为[12,8,pi]（pi表示停车时车头朝向角为π，后文均采用此种表述）。混合状态A*算法的结果图2所示。方点代表汽车的起点，圆点代表终点，点线代表算法的历史前向搜索记录，点划线代表算法的历史后向搜索记录，实线是最终的运动轨迹。

图2 混合状态A*算法的搜索结果

根据优化算法得出的结果，可以计算出此时的速度图像、加速度图像，来近一步分析优化后的结果。

图3是根据优化后的结果得出的汽车状态图像。从中可知优化后的质心速度大多数时间稳定在3 m/s左右，而质心加速度则变化幅度比较大。实际上，汽车在行驶过程中，最大加速度一般在10 m/s2左右，此处计算出的加速度已经超过了实际的最大加速度。在这种搜索步长下，优化算法对混合状态A*算法搜索出的结果优化效果不明显。同时，又由于缺少不等式约束，导致计算出的加速度容易超出汽车实际的最大加速度。因此算法值得进一步的改进。

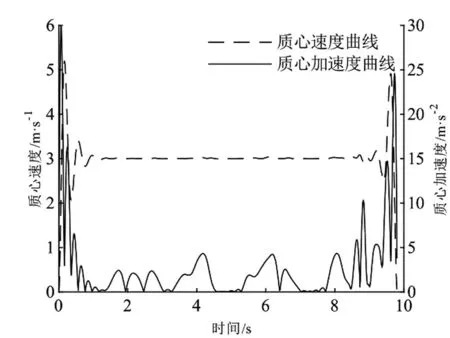
图3 优化后汽车的运动速度和加速度

优化过程需要花费的时间也是优化算法十分重要的评价指标。基于最小冲击度的优化算法的运行速度实际上是比较快的。如表1所示，Hybrid A*代表混合状态A*算法的运行时间，QP和CF则分别代表二次规划求解器和闭式解求解方法的运行时间。在混合状态A*算法搜索出50个路径点的条件下，基于二次规划求解器的求解算法和基于闭式解的求解算法生成了576个系数，共7 224个数值。在这种计算规模下，MATLAB中的3次试验结果显示，不论是基于二次规划求解器的求解方式，还是基于闭式解的求解方式，优化算法的计算时间都不会超过0.1 s。即便是加上混合状态A*算法的耗时，运算时间也基本保持在0.5 s左右。

表1 算法运行时间比较 s

对于前文中（图3）加速度超出实际范围的情况，可以在优化之后再单独加一层速度规划层，便可以基于优化结果得出更好的速度和加速度结果。此处采用梯形速度分配公式来做速度规划，设置最高速度为3 m/s，便可以得出如图4所示的结果。

图4 速度、加速度重规划

本文采用的地图是栅格地图，以上试验全部是在静态层进行的试验。实际应用中，从起点到终点的运动过程中，汽车需要不断地感知周围的环境。在静态地图中，当汽车接近突然出现的障碍物或汽车运动到某位置才检测到周围具有障碍物时，可能导致之前规划的轨迹失效，需要规划器重新做出规划。所以此处给汽车栅格地图障碍物层加入障碍物信息，并给汽车加上传感器再次进行试验。

假设汽车可以感知到周围环境120°范围内的障碍物，探测范围在[0,20]之间。设置汽车起始位置为[9,16,0]，最终停在停车位上的状态为[22,8,pi]。用实线代表当前算法搜索出的轨迹，虚线代表历史搜索出的轨迹，而辐射范围代表传感器可探测到的范围，方块代表检测到障碍物后膨胀的方格。需要注意的是，如果规划的轨迹存在“局部碰撞”（未来可能发生碰撞），算法也会重新规划路径。最后图5显示了2种算法到达终点附近的运动历史轨迹，由虚线可知，2种算法均会做出多次重新规划。同时，优化算法在某些障碍物附近的曲率变化略小于混合状态A*算法。

图5 两种算法的最终运动轨迹

直观的来看，基于优化算法的最终轨迹相对于混合状态A*算法的曲率变化率较小，但是还是不能改变混合状态A*算法在某些点距离障碍物较近的缺点。虽然这种缺点是有可能通过调整混合状态A*算法的参数来解决的，但仅从优化的角度来看，基于最小冲击度的优化算法是很难解决这样的问题的。

4 硬约束下基于最小冲击度的优化模型

由于很多路径规划算法会将汽车视为点来进行路径规划，这导致某些规划算法规划出的路径超出了汽车的正常行驶范围，且不能保证车内乘客的舒适性。为提高汽车在运动过程中的舒适性，实际工程中会根据最小冲击度的大小对当前运动情况进行调整。所以，在本文对混合A*算法的结果基于最小冲击度进行优化，但是发现基于最小冲击度的优化算法在大步长时生成的轨迹会碰撞到障碍物（图6a）。如果假设在自由空间EFree存在一条从起点到终点的无碰撞“走廊”（图6b），规划出的轨迹位于走廊之内，那么最终的轨迹无论如何都不可能发生碰撞。因此本文尝试采用此方法求解最终轨迹。

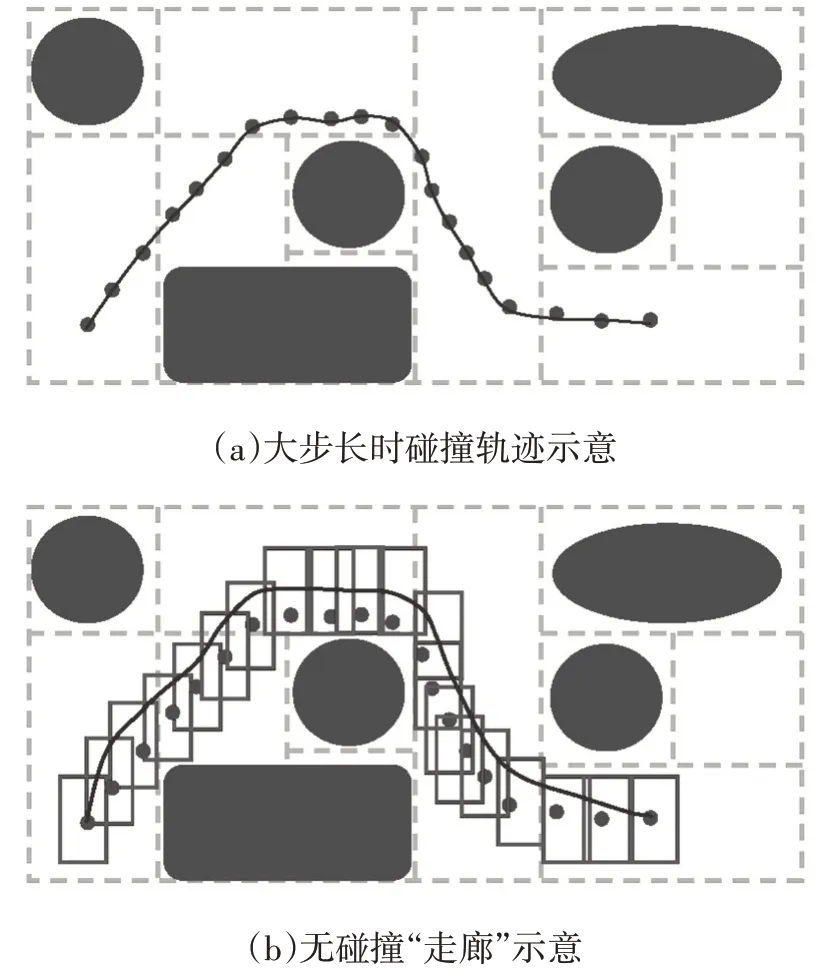
图6 算法改进策略

硬约束下基于冲击度的优化模型就是要将最终的目标函数化为带有不等约束的目标函数，此处依旧按照解凸优化问题的求解器进行求解。与之相反的，软约束下的优化模型就是要将所有的约束写入目标函数中，最终使用梯度下降法、牛顿法或拟牛顿法进行求解。

本文基于贝塞尔曲线实现轨迹的无碰撞，其优点如下：

（1）传统的基于贝塞尔曲线的轨迹规划方式中，不同阶数的贝塞尔曲线对应着不同数量的控制点，业内经常利用4次和3次贝塞尔曲线来做插值[50-51]。通常的做法是，根据速度、加速度、贝塞尔曲线的阶数约束，先得到相应阶数下从起点到终点的控制点，然后再根据控制点计算出最终的轨迹。而本文中，贝塞尔曲线的阶数是固定的，前文已经证明基于最小冲击度的轨迹可以用5次多项式来表示，所以此处的伯恩斯坦多项式也是5次多项式。

（2）本文将首先根据规划算法（混合A*类算法）规划出全局的路径点。然后，在规划出的路径点附近形成一系列连续的“走廊”，这些“走廊”全部位于自由空间EFree，最后在走廊中生成贝塞尔曲线。

（3）传统的贝塞尔曲线无所避免的会出现“打结”现象，而本文中只固定起点和终点，而“释放”其它规划的路径点，最终形成的多段贝塞尔曲线可以避免“打结”。

（4）本文中利用贝塞尔曲线来构建一个基于最小冲击度的优化问题，属于优化问题范畴；传统贝塞尔插值式的路径规划算法属于插值式的规划算法，属于规划范畴。

本文中“走廊”内规划的思想也与自动驾驶时代“高精度地图+管道式行驶”的精神相契合。

4.1 贝塞尔曲线

由规划算法得出的路径点得到“走廊”之后，如何确保最终生成的轨迹不超出走廊是目前需要考虑的问题。而贝塞尔曲线无疑是一个比较好的选择，只要贝塞尔曲线的控制点都在“走廊”以内，那么贝塞尔曲线也在“走廊”以内。这个逻辑之所以成立，是因为贝塞尔曲线具有凸包性。贝塞尔曲线对应的多项式具有以下形式：

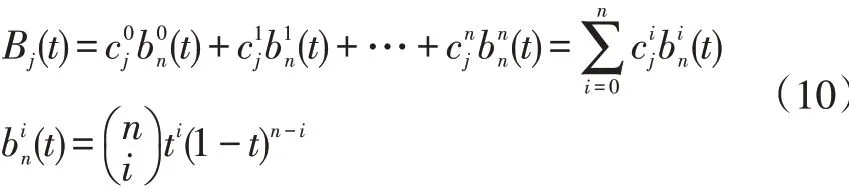
式中，Bj(t)为各走廊内贝塞尔曲线表达式为贝塞尔曲线的控制点;为各控制点的系数表达式，与控制点个数与时间t有关。

本文中主要利用了贝塞尔曲线的以下性质：

（1）贝塞尔曲线的凸包性，即由一组控制点形成的贝塞尔曲线始终位于这组控制点组成的凸包以内。

（2）贝塞尔曲线的导数仍然是贝塞尔曲线。

（3）贝塞尔曲线中的t始终在[0,1]区间内。

4.2 硬约束下基于最小冲击度优化模型的建立

由于仍然是基于最小冲击度的一维优化模型，所以硬约束下最小冲击度模型的目标函数仍然与式（9）相似，但需要将一般多项式转化为伯恩斯坦多项式。另一方面，为了解决速度、加速度会超出计算范围的问题，还需要给模型加上不等式约束。等式约束仍旧是连续性约束（位置连续、速度连续和加速度连续）、边界约束（初始时刻和终止时刻的位置约束、速度约束和加速度约束）和中间点位置约束。由于此处的目标函数已经转化为伯恩斯坦多项式，所以此处所有的约束也需要转换为相应形式。

对于如下形式的一般多项式：

式中，pj(t)为n阶伯恩斯坦多项式；为多项式中的算子。

要将其转化为式（10）所示的形式，需要建立一个映射矩阵如：

式中，p为一般多项式（11）中的系数向量；c为贝塞尔曲线多项式（10）中的系数向量；M为系数向量p、c的映射矩阵。

添加速度约束和加速度约束：

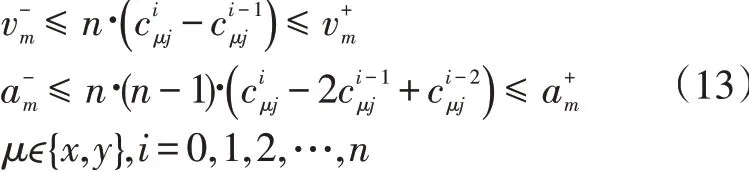
根据这些目标函数和约束，可以最后推到出多段硬约束下基于最小冲击度下的优化模型如式所示：

式中，min式为凸目标函数；s.t.式为约束函数。

最终，问题转换成了一个典型的凸优化问题，可以采用求解凸优化问题的方法来求解相应的系数。

4.3 对混合状态A*算法的优化结果

由于基于最小冲击度的优化对混合A*的优化效果并不明显，且加速度会超出实际汽车的最大加速度。本文采用硬约束下基于最小冲击度的优化算法对混合状态A*算法进行优化，当路径点距离障碍物较近时，在原来路径点基础上得出走廊会存在和障碍物重合的现象。这时得出的最终轨迹也会因此发生碰撞，优化结果应在无碰撞的基础上，对原来的路径点做出优化。

本文采用矫正走廊位置的方法，即将当前存在碰撞的“走廊”向自由空间挪动。如图7，对于有一个顶点和障碍物重合的情况，可以沿着对角线附近方向微调，不一定沿着对角线方向，因为这样的调整方法可能会造成“走廊”不连续的情况。对于2个顶点和障碍物重合的情况，只需要将走廊中心沿着另一端平移即可。而对于4个顶点与障碍物重合但中心不重合的情况，则需要沿2端的连线方向缩小走廊，然后再平移走廊。所以，可以得出图8的走廊调整算法。

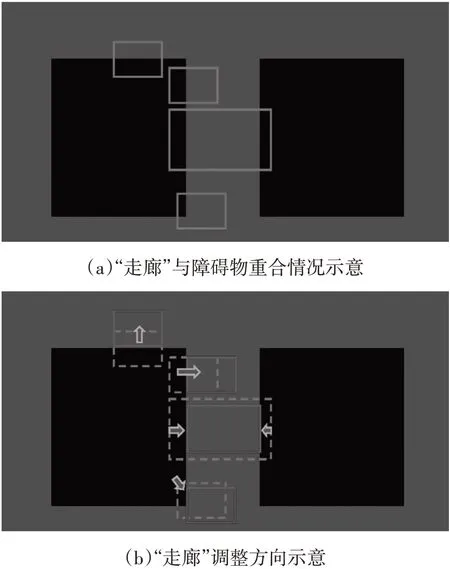
图7 “走廊”调整策略

图8 “走廊”调整算法

设置初始状态为[9,16,0],最终状态为[12,8,pi]，绕过障碍物后汽车需要停在停车位上。星点代表了由混合状态A*算法搜索得到的路径点，方框内的实线是混合状态A*算法得出的轨迹，菱形是根据混合状态A*算法搜索得到的路径点调整的“走廊”的中心，方框构成了最终的“走廊”。在不改变其它条件的情况下，调整“走廊”在x和y方向上的长度都为3 m。如图9所示，对比起走廊约束分别为2 m的结果，更大的约束下得出的优化结果与混合状态A*得出的轨迹差别更大。

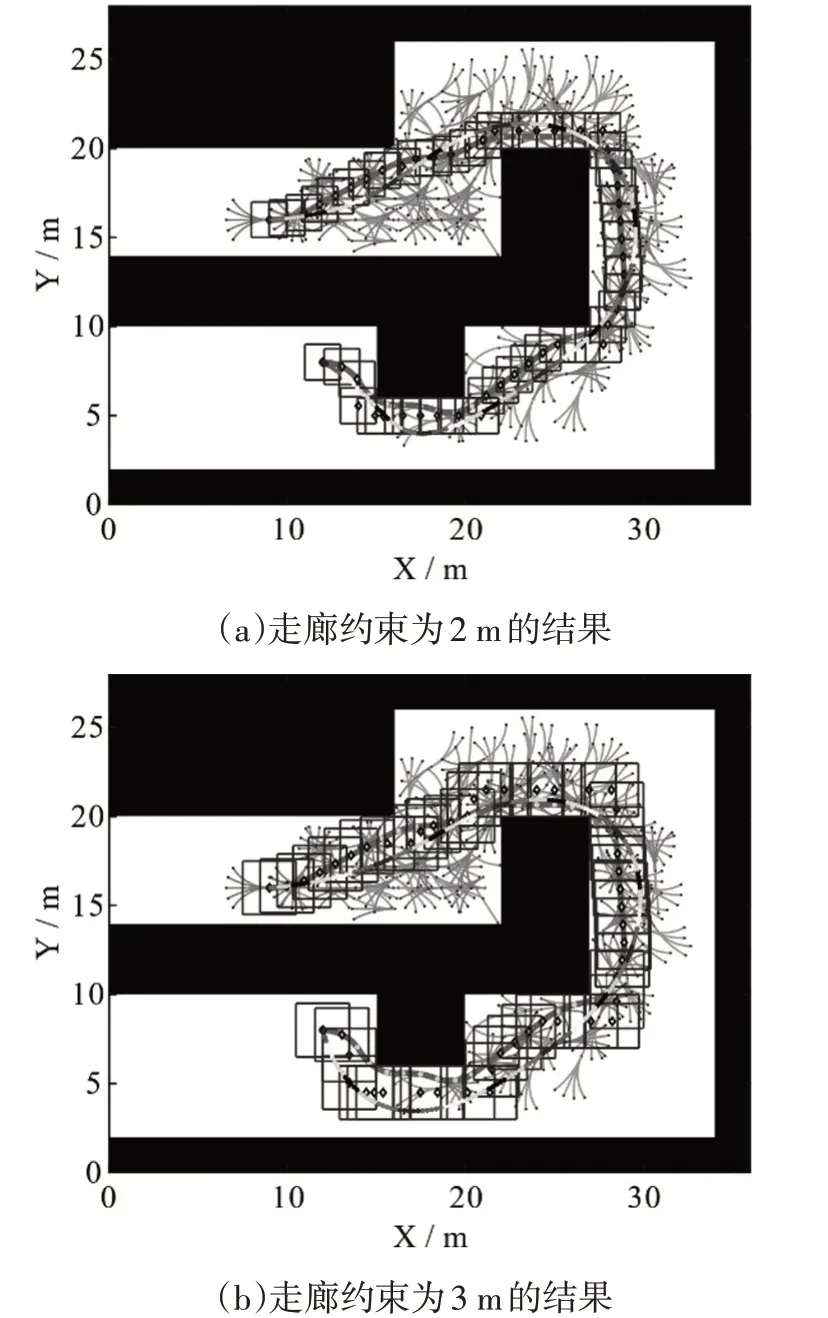
图9 不同走廊约束下的优化结果

表2是在混合状态A*算法搜索出49个路径点，优化算法得到588个系数，4 949个路径点的条件下，在MATLAB中混合状态A*算法以及硬约束下的优化算法的运行时间。此处进行了3次试验。

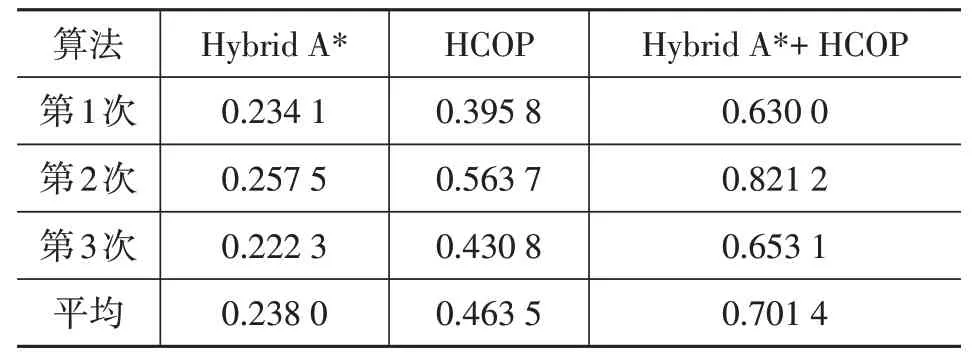
表2 硬约束下基于最小冲击度优化算法运行时间 s

在相同条件下试验，最终的走廊不再与障碍物重合，所以最终的轨迹也不再发生碰撞。不过从运行时间来看，优化算法的运行时间并不快。与上一节类似，最后需要在栅格地图的障碍物层加入障碍物信息，给汽车加上传感器，以探究动态过程中算法的表现。从起点到终点的运动过程中，汽车需要不断地感知周围的环境。在地图中，当汽车接近突然出现的障碍物或汽车运动到某位置才检测到周围具有障碍物时，需要规划器重新做出规划。

4.4 对优化结果的评价

此处对图9（b）的结果进行进一步讨论。已知初始状态为[9,16,0]，最终状态为[12,8,pi/2]，绕过障碍物后汽车需要停在停车位上。混合状态A*算法的最小转弯半径为2 m，搜索步长为2 m。设置“走廊”在x和y方向上的长度都为3 m。汽车的最大速度为20 m/s，汽车的最大加速度为10 m/s2。

在得出从起点到终点的路径之后，对多项式求导便可以得出其速度、加速度和冲击度。由此获得速度曲线、加速度曲线和冲击度曲线如图10和图11。由这2幅图可知，优化后的曲线是近似梯形的，最高速度是3.87 m/s，对应的速度代价值，即路程为60.85 m。同时，最大加速度也在合理范围内，为3.97 m/s2。除去起始和终止时刻，冲击度也较小，优化后的代价值为

图10 速度曲线

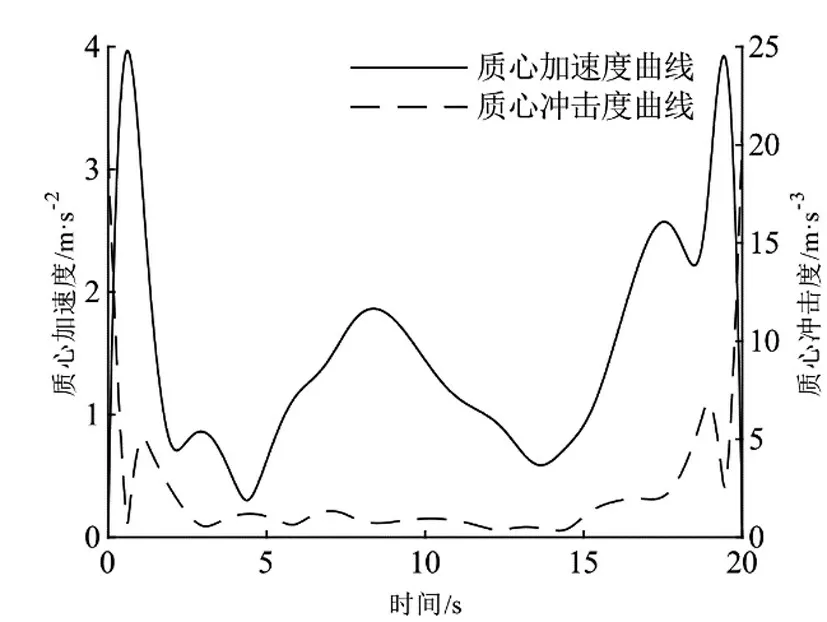
图11 加速度和冲击度

213.66 m2/s5。

至于优化前后轨迹的曲率，可以通过优化前后的路径点来计算。除去起点和终点的曲率无法计算外，其它点最终都可以得出一个曲率值。优化前有320个路径点，最终得出318个点的曲率。优化后的点有505个点，最终得出503个点的曲率。可由图12知，优化前的曲率振荡振幅很大。由于优化前后计算曲率的方法一致，考虑到可能是由于优化前的点过于稠密，所以删除点的个数为原来的1/4，便可得出图12b所示的曲率。此时，优化后的曲率是小于优化前的曲率。由于数值计算的不稳定，所以初始和终止的曲率会比较大。事实上，当具体分析起点和终点的曲率数值时，可以看出初始时刻，只有4个点是过大的，终止时刻，则有8个点较大，但是相比起505点，这12个点只占2%左右。也就是说，绝大多数计算出的曲率是在正常范围以内的。

图12 优化前后的曲率

最后，分析优化前后路径点距离周围障碍物的最小距离，从图13可知，优化前路径点到障碍物的最小距离为0.20 m，而优化后路径点到障碍物的最小距离为0.30 m。优化前距离的代价值为6.19，而优化后为3.76，在距离这个评价指标上，优化后的路径点也是优于优化前的。

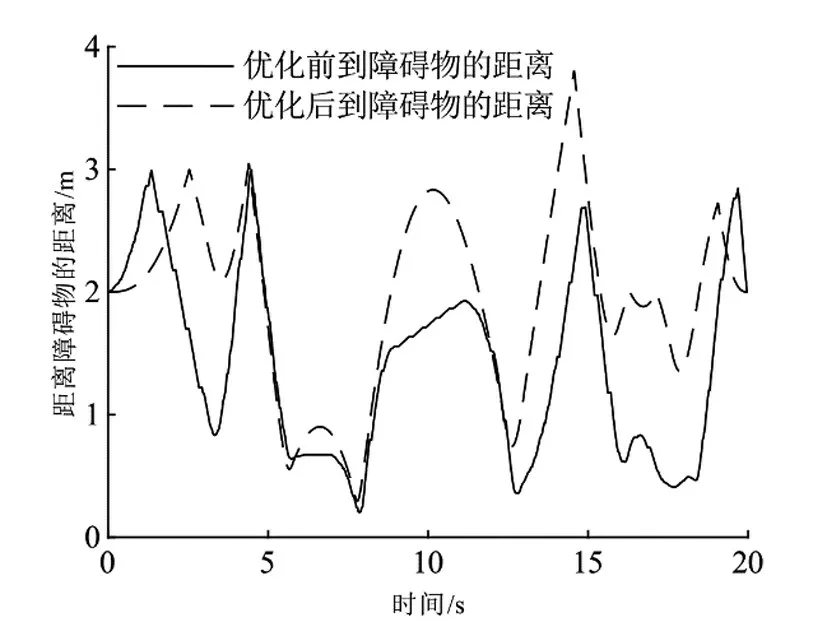
图13 优化前后路径点到障碍物的距离

从上面的试验结果可以看出，优化后的轨迹不仅是基于最小冲击度，同时也可以得出近似梯形的速度曲线。优化后的曲率和到障碍物的距离也优于优化前的曲率和距离。这说明硬约束下基于最小冲击度的优化算法在整体上是优于优化前的算法，可以在保证舒适性的前提下，得出较优的轨迹，具有应用于实际场景的潜力。

5 结语

本文主要针对自动驾驶汽车的轨迹优化问题展开研究，聚焦如何通过优化手段，得出汽车最终可行驶优化轨迹的同时提高自动驾驶汽车的舒适性。主要研究了最小冲击度下汽车的轨迹生成问题，基于硬约束下的最小冲击度模型对原有的优化模型进行了改进。对比分析后可知：虽然硬约束下的优化算法计算速度不占优势，但是优化后的轨迹无碰撞，且在基于最小冲击度的前提下，曲率更小、加速度保持在正常范围内、距离代价值也降低了39.3%。总体上硬约束下基于最小冲击度的优化算法解决了原有模型优化后相关状态量超出实际范围及优化后出现碰撞的问题，使得原有模型更加适合于非结构化空间场景。