基于改进迁移学习和多尺度CNN-BiLSTM-Attention的短期电力负荷预测方法

欧阳福莲，王 俊，周杭霞

基于改进迁移学习和多尺度CNN-BiLSTM-Attention的短期电力负荷预测方法

欧阳福莲，王 俊，周杭霞

(中国计量大学信息工程学院，浙江 杭州 310018)

针对目标域负荷数据样本不足导致模型训练不充分从而预测精度不高的问题，提出一种改进的分层级迁移学习策略结合多尺度CNN-BiLSTM-Attention模型的短期电力负荷预测方法。设计串并行相叠加的多尺度CNN作为特征提取器，把提取到的特征作为输入传递到两层BiLSTM结构进行进一步的学习，引入注意力机制调节捕获的信息向量权重。按照基础模型的结构划分层级，将源域数据按照拟合优度值的高低输入至模型进行分层级的迁移学习训练，保留每一层最优的训练权重，之后使用目标域数据对模型进行微调得到最终的预测模型。经实验证明，所提出的多尺度CNN-BiLSTM-Attention模型能有效提高负荷预测精度，在负荷数据样本不足时，改进的分层迁移学习策略相比于直接迁移学习能有效降低预测误差。以目标域6个月数据为例，MAPE指标降低13.31%，MAE指标降低15.16%，RMSE指标降低14.37%。

负荷预测；卷积神经网络；双向长短期记忆网络；注意力机制；迁移学习

0 引言

电力负荷预测作为电力系统调度的基础，准确的预测对电力系统的运行规划有重要的指导意义[1]。国内外学者对短期电力负荷预测进行了大量的研究。以自回归移动平均模型[2]为代表的线性方法简单可行，但电力负荷容易受到气象、时令、节假日等多种因素的影响[3]，线性方法对于短期电力负荷预测中的非线性因素的影响难以评估，预测精度得不到保证。应用于短期负荷预测领域常用的机器学习模型有随机森林算法[4]、支持向量回归(support vector regression, SVR)[5]、极限梯度提升机(extreme gradient boosting, XGBoost)[6]和极限学习机(extreme learning machine, ELM)[7]等，这些方法在处理非线性问题上展现出较大的优势，但是仍然存在数据相关性处理困难、特征维度多、数据规模大和处理速度慢的问题[8]。随着深度学习的不断发展，以卷积神经网络(convolutional neural networks, CNN)[9]和循环神经网络(recurrent neural network, RNN)及其改进方法(如长短期记忆(long short-term memory, LSTM)[10-12])为代表的神经网络模型在短期负荷预测领域取得了良好的预测效果。但是基于单链结构的LSTM仅能学习正向时序关系，BiLSTM(Bi-directional LSTM)[13-14]优化了LSTM神经网络对历史数据的全局信息学习不充分和忽略了前后时间的关联性的问题，其双向的结构使其可以学习序列正向和逆向的时序关系。文献[15]验证了在预测准确度上BiLSTM优于LSTM。为了克服单一模型在电力负荷预测精度上的不足，组合模型利用不同基础模型对不同特征处理能力的优势来提高整体的模型性能，得到了广泛的应用[16-17]。文献[18]将CNN与BiLSTM组合，结果表明在预测误差方面优于LSTM、BiLSTM和CNN-LSTM，是目前预测精度最高的方案。注意力机制是针对编码器-解码器结构存在信息丢失等问题提出的改进机制[19-20]。文献[21-22]在CNN- LSTM网络上附加注意力机制用于特征选取。

现有的短期负荷预测研究方法主要利用了负荷数据的历史数据而不考虑其他负荷数据的有效信息，并且需要在大量的数据样本下进行实验，对于数据样本不足的情形，进行准确的负荷预测依然存在困难。目前针对小样本数据的预测方法主要有迁移学习方法，传统的迁移学习方法将数据整体迁移，没有考虑负荷数据不均衡的特点，数据局部特征学习不够充分，预测准确率仍然得不到保证。本文针对电力负荷数据样本不足导致模型训练不充分从而预测精度不高的情形，提出一种融合分层级迁移学习和多尺度CNN-BiLSTM-Attention网络模型的短期电力负荷预测方法。多尺度CNN将不同大小的卷积核串行叠加和并行拼接对特征进行有效学习，与两层BiLSTM相连改善了单层BiLSTM在负荷预测空间特征上提取不充分的问题，结合注意力机制，融合分层级的迁移学习算法解决了预测精度不高的问题。以美国典型气象年不同区域的负荷数据进行实验，证明了本文方法的有效性。

1 基础模型构建

本文提出的基础预测模型结构包括输入层、多尺度CNN层、两个BiLSTM层和Attention层，之后通过全连接层(Dense)将结果映射到一维进行输出。模型结构图如图1所示。

图1 多尺度CNN-BiLSTM-Attention基础模型结构图

图1中：U表示卷积操作；表示滑动窗口大小；表示特征数目；Concatenate表示特征拼接操作；Dense表示全连接网络；1—8表示基础模型进行分层迁移学习时划分的层级。

1.1 输入层

将预处理后的负荷数据、日期数据、节假日以及时令信息输入基础模型中，采用每个时间步滑动窗口大小的外部特征和负荷值作为输入，时间步滑动窗口大小为，通道数为，在时刻具体的输入如式(1)、式(2)所示。

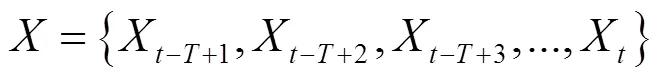
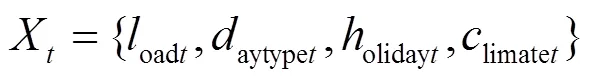
1.2 多尺度CNN层

本文基础模型中的多尺度CNN层使用不同尺寸的卷积核从不同跨度的时序邻域内提取特征，大尺寸邻域内每项数值产生的影响更小，输入数据中的波动以及噪点对输出特征的影响更弱，但是也容易产生平滑过度的问题。与之相对，小尺度卷积核可以更好地保留输入数据中的信息，但也更容易受到噪声的干扰。因此使用不同大小的卷积单元来提取不同时序尺度的特征，使用串行叠加和并行拼接的方式完成特征融合并输出多维特征。本文使用的时序特征提取单元的卷积核大小为1、3、5、7，其中Kernel=1的卷积核用来进行数据升维。多尺度CNN层的运算可以表示为式(3)—式(7)所示。

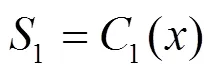
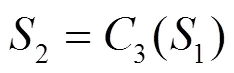
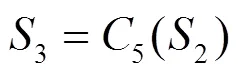
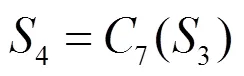
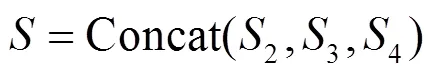
1.3 BiLSTM层

在周期性数据中，表现出以周负荷的消耗为单位呈现极大相关性，以日负荷的消耗为单位呈现较大相关性的特点。使用BiLSTM对负荷数据进行周期特征提取，利用BiLSTM网络分别计算前向传播状态和反向传播状态，计算过程如式(8)—式(10)。

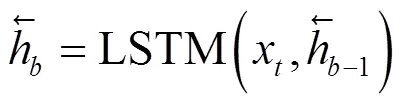
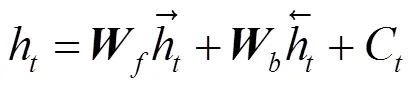
1.4 Attention层

时间序列输入较长时，容易出现信息丢失的问题，使用Attention机制调整注意力系数以提高模型整体的记忆能力。具体的过程如下。

(11)

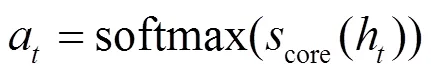
2) 赋予各历史状态对应的注意力权重，加权平均得到经注意力机制优化的输出结果，如式(13)所示。

1.5 输出层

在Attention层之后连接一个激活函数为sigmoid的全连接层将数据转化成一维，得到最终的输出。

2 分层级迁移学习

迁移学习把知识从一个或多个源域迁移到另一个目标域，利用已知某领域的知识求解不同但相关领域的问题[23]，已经在故障诊断等多个领域得到应用[24]。迁移学习无需训练数据，和测试数据保持独立同分布，因此对目标域的训练不需要从头开始，加快了训练速度。本文改进的分层级迁移学习过程概括如下。

1) 源域数据划分。对源域数据按照拟合优度从低到高排序划分为组，取决于基础模型的层数，在本文中= 8。

2) 分层迁移学习。将排好序的源域数据输入多尺度CNN-BiLSTM-Attention模型的不同层级进行分层迁移学习，每组数据依次输入模型的不同层进行训练，采用合适的冻结策略，得到目标域负荷最终的预训练权重。

3) 模型微调。固定冻结层参数，采用目标域数据对非冻结层参数进行微调。

2.1 源域数据划分

为寻找源域与目标域数据更加相似的数据，先对源域的数据进行拟合优度划分。目标域数据经过滑动窗口输入到多尺度CNN-BiLSTM-Attention模型(基础模型)中进行训练，得到一个初始预测模型；之后，源域数据也通过滑动窗口输入到该初始预测模型中，每一个时间序列滑动窗口均可得到一个预测结果，该预测结果的优劣程度用拟合优度(2)衡量；将源域数据中拟合优度小于特定值的数据剔除，认为其与目标域数据拟合程度不高；剩余数据按照拟合优度高低划分区间后按照区间排序。源域数据的划分过程如图2所示，图中表示基础模型。

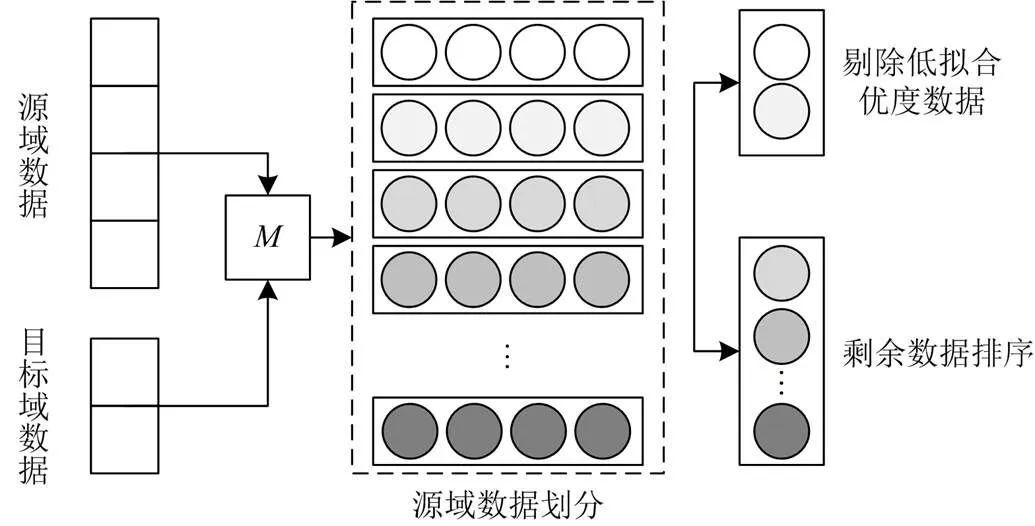
图2 源域数据的划分过程

2.2 分层级迁移学习

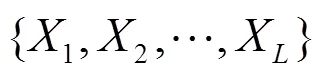
改进的分层迁移学习策略实现过程： Input:源域数据X，目标域数据Y，验证集数据T，基础模型M。 Output:Wend // 基础模型经过预训练后最终的输出权重 /*步骤1. 获得基础权重并对源域数据进行划分*/1: W0 ← Train model M with data Y; /*使用目标域数据在基础模型上训练，获得初始权重W0*/2: R2(X,M(W0)) ← Test X with M(W0); /*M(W0)表示加载了初始权重的模型M, R2(X,M(W0))为数据X在模型M(W0)训练得到R2；3: {X1, X2, …, XL} ← DividedX ; /*将数据X划分为L组，每组根据R2值的大小排序*/ /*步骤2 分层迁移学习*/4: i = 0; /*i表示当前层5: whilei < L /*L表示总层数6: i+= 1;7: Load Wi-1; /*加载上一层的权重，其中Wi代表第i层迁移学习得到的权重8: Unfreeze Fi; /*解冻当前层，其中Fi代表冻结第i层9: Wtmp← Train model M with data Xi; /*使用第i组数据训练模型，获得权重Wtmp*/10: if Loss(T, M(Wtmp)) <= Loss(T, M(Wi-1)) /*比较当前层和上一层在验证集上的损失值，如果损失值下降，执行下一步操作*/11: Wi = Wtmp; /*保存此时的临时最优权重*/12: j = i;13: whilej > 1 /*若当前层非第一层*/14: Unfreeze Fj-1; /*解冻上一层*/15: Wtmp1← Train model M with data Xj ;/*此时的模型M为解冻当前层和上一层的结构*/16: if Loss(T, M(Wtmp1)) <= Loss(T, M(Wi))17: Wi = Wtmp1; /*则此时的Wi即为当前层的最优权重*/18 j-= 1;19 continue;/*重复以上步骤找到每层的最优权重*/20: else /*如果预测误差没有下降*/21: Wtmp← Train model M with data Xi-1; /*使用上一层数据训练模型M22: if Loss(T, M(Wtmp)) <= Loss(T, M(Wi-1))23: Wi = Wtmp;/*保存最优权重*/24: else25: Wi = Wi-1;26: continue;

2.3 模型微调

最后一层迁移学习完成后，使用目标域的训练集对预训练模型进行部分参数微调，冻结除最后的全连接层之外的所有层，并对全连接层的权重进行初始化，给定一个较小的学习率，只需要训练修改部分网络参数，而不需要训练整个网络。

3 算例分析

3.1 数据集描述与处理

本文的数据是从Open Energy Data Initiative (OEDI)(https://data.openei.org/submissions/153)网站上获取的美国各州一年的负荷数据。选用9个城市不同医院设施的用电负荷数据作为实验数据集，其中8个不同区域的医院设施用电负荷数据作为源域数据，剩余一个区域用电负荷数据作为目标域数据。数据粒度为每小时1个点，源域合计8×8760条数据，目标域12个月共8760条数据，训练集、测试集和验证集按照10:1:1划分。使用模拟的缺失数据分别为目标域1/4、2/4、3/4的数据量样本，验证集和测试集与数据充足时相同，训练集为除去验证集和测试集之后的剩余数据。数据集的具体划分示意图如图3所示。

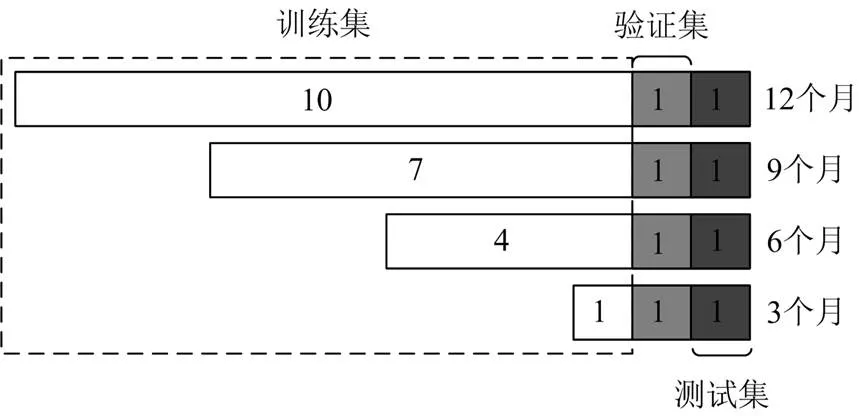
图3 数据集划分示意图

由于选用的数据集的电力负荷数值在500~ 1500 kWh内波动，数值跨度大，不利于模型的训练，为了消除不同特征数据量纲的影响，先对数据进行最小最大归一化处理，目标域负荷数据分布情况如图4所示。

图4 数据分布情况

图4上图为数据整体分布情况，下图为截取的部分夏令时(左)和冬令时(右)的负荷分布，包含了7个波峰，依次对应周一至周日的负荷情况。由图4可知，电力负荷在夏令时波动比较规律，冬令时负荷的峰谷值波动较大。总体上负荷表现以周为单位的周期性变化，其中周一至周五的日负荷值较高，波动有序，周六相比工作日负荷值要低，周日比周六又更低；其中，若某天为重大活动或节假日，当天的负荷值更低。由此总结出7个特征：节假日、非节假日、工作日、周六、周日、夏令时、冬令时。为方便模型计算，将文本数据转换为数值型数据，对数据集的上述特征进行标签编码，各非数值特征编码如表1所示。

表1 特征编码

3.2 评价指标选取

本研究使用平均绝对误差(mean absolute error, MAE)、平均绝对百分比误差(mean absolute percentage error, MAPE)、均方根误差(root mean square error, RMSE)三个指标对本文的实验结果进行评价。评价指标计算公式如式(15)—式(17)所示。

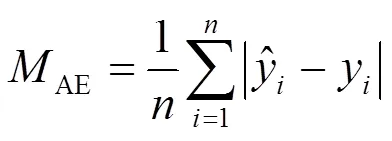
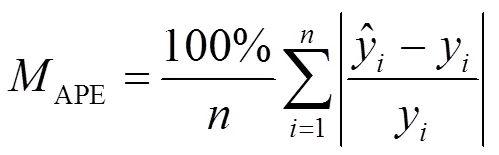
3.3 模型参数设置

在模型的训练和预测过程中涉及许多超参数，超参数的设置影响着最终的预测结果，经过多次预训练和优化调整，各项参数设置如表2所示。

3.4 实验结果

3.4.1预训练模型性能

为了更好地验证本文提出的多尺度CNN- BiLSTM-Attention神经网络模型的性能，选取了在负荷预测中应用较为广泛的ARIMA、LSTM、CNN-LSTM、CNN-GRU、BiLSTM-LSTM、SVR、XGBoost、ELM模型作为对比模型。各模型预测误差对比结果如表3所示。

表2 参数设置

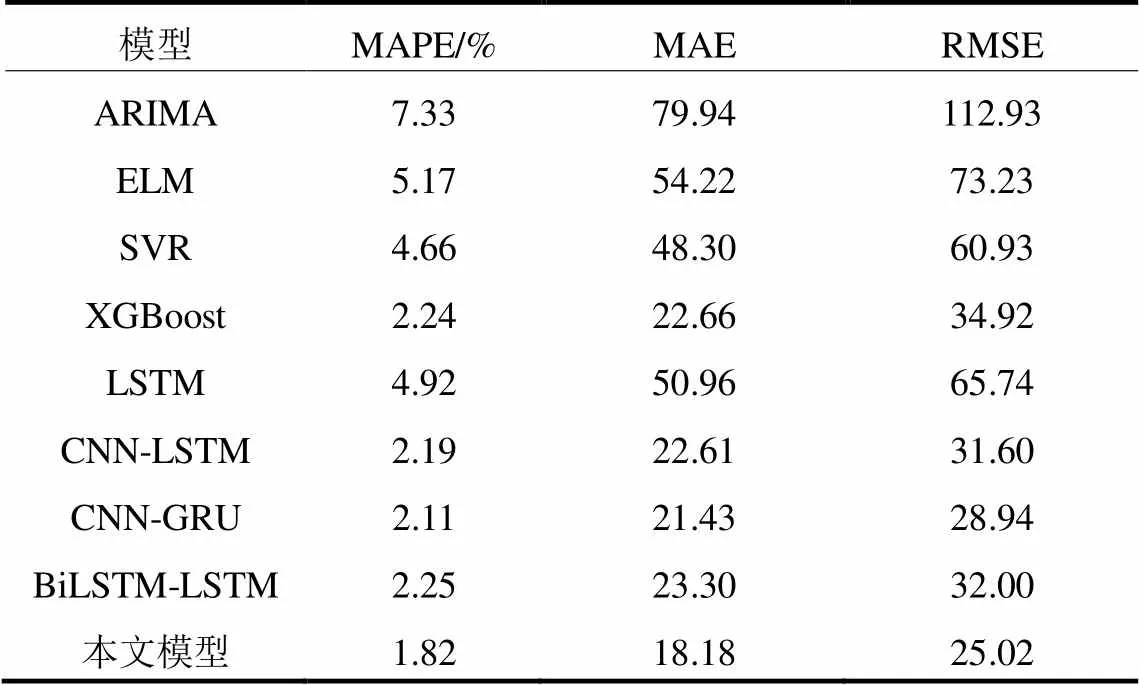
表3 不同模型预测误差对比结果

由表3的预测结果进一步分析可知，ARIMA模型是一个统计模型，对于负荷数据的非线性规律难以捕捉，预测误差较大；以ELM、SVR为代表的机器学习模型相比于统计模型，在预测精度上有一定的提升，其中，XGBoost模型作为集成模型采用boosting的思想，预测性能表现较好；深度学习模型中，LSTM单向的循环网络不能充分捕获长时间序列的有效信息，预测效果不理想；组合模型均能不同程度地改善上述问题，相较于单模型预测误差下降明显。本文模型充分结合了多尺度CNN、BiLSTM和注意力机制的优势，在三个评价指标上均表现最优。

为了证明本文提出模型中的每一模块的重要性，针对本文模型的各个模块进行消融实验，为了控制变量保证实验的严谨性，只去除或者改变单个模块，其余内部参数保持一致。消融研究实验说明如下：

1) NoAttention表示不使用注意力机制模块；

2) Linked表示不同尺度CNN采用串行方式连接；

3) Parallel表示不同尺度CNN采用并行方式连接；

4) 单层BiLSTM表示只使用一层BiLSTM；

5) 三层BiLSTM表示使用了三层BiLSTM。

消融实验的对比结果如表4所示。

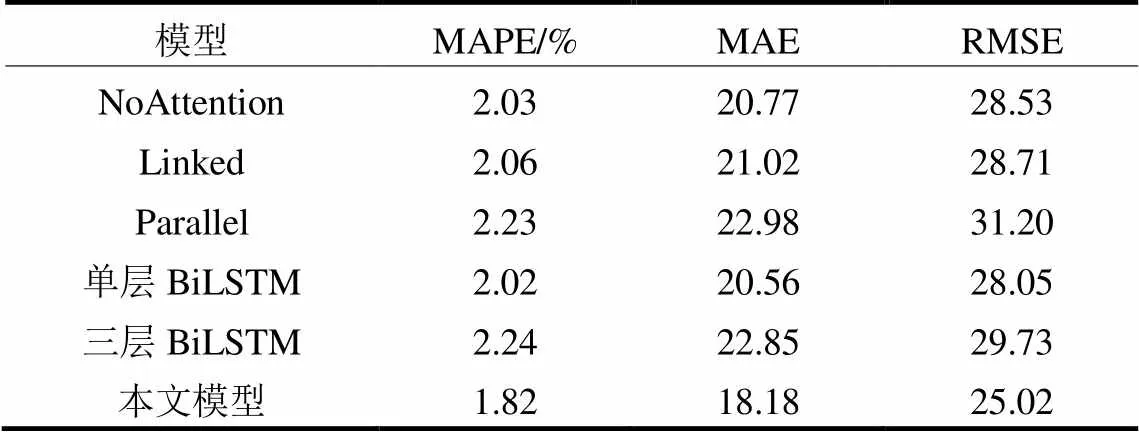
表4 消融研究实验对比结果

从表4中的预测误差结果可以看出，本文提出的模型在MAPE、MAE和RMSE值上优于其他对比模型，进一步分析，主要原因在于以下几方面。

1) 多尺度CNN采用不同尺寸的卷积核提取特征，然后采用串行叠加和并行拼接的方式完成特征融合得到多尺度邻域特征，从而输出的特征中既包含平滑后的特征，也保存了原始输入的特征。在模型训练过程中，后续的网络结构可以学习分析这两种特征，从而在一定程度上实现了平滑输入数据，并且避免信息丢失。

2) CNN与BiLSTM组合模型合理利用了CNN提取数据局部特征以及BiLSTM隐藏层权重反向传播逐步优化训练权重的优势，充分考虑了特征的影响和数据的时序变化。

3) BiLSTM的双向结构使其可以学习序列正向和逆向的时序关系，对历史负荷数据的全局信息进行进一步的学习，其两层的BiLSTM结构弥补了BiLSTM空间信息提取不足的缺陷，避免了不必要的时序信息的丢失。

4) Attention机制的引入可以有效地对存在关联性的时间序列长距离数据特征进行挖掘，对于长序列数据和多维输入特征数据引入注意力机制可以提升模型的特征发掘能力。

3.4.2分层级迁移学习性能

采用多尺度CNN-BiLSTM-Attention作为基础模型，根据基础模型结构划分为8层，每一层迁移学习均保留当前层的最优权重，最后使用目标域的负荷数据对基础模型进行参数微调。以目标域6个月数据为例，不同迁移层数的预测误差及使用目标域数据进行微调后的预测误差如图5所示。

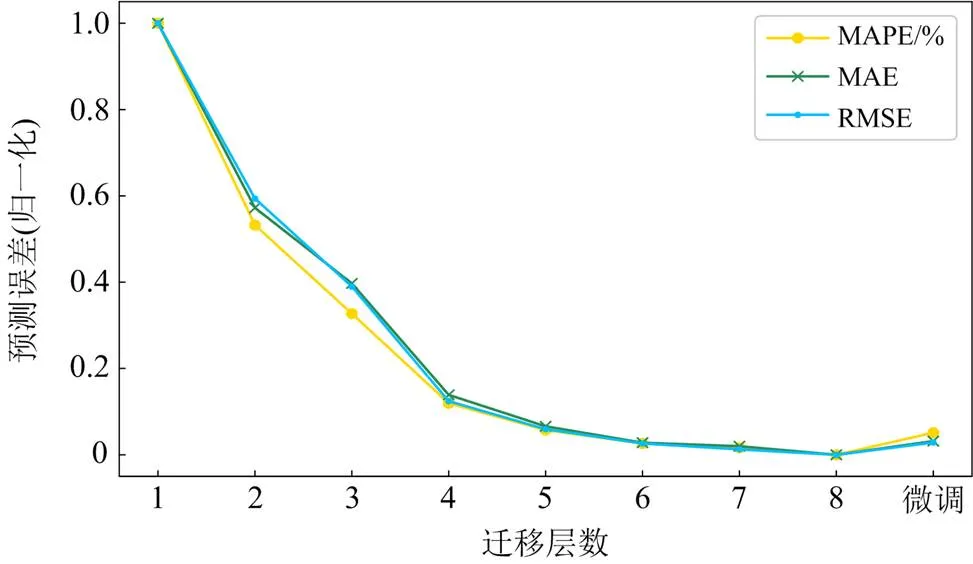
图5 不同迁移层数的预测误差

由图5可知，随着分层迁移层数的不断增加，每一层迁移学习在测试集上的预测误差均有所下降，下降幅度逐渐平缓，迁移至第8层后，预测误差趋于一个较小值，证明了本文方法分层迁移的有效性。然而，使用目标域少量数据对模型进行微调后，预测误差反而有小幅度的增加，这是由于源域数据进行迁移学习时使用的验证集和目标域训练基础模型时相同，并且本文选取的源域数据和目标域数据样本较为相似，所以在模型进行微调时，使用的目标域数据相较于预训练模型的质量较差，微调后的预测误差反而增大。在迁移学习至第8层时，预测误差在各项评价指标下均处于一个最优值，故本文选取预训练模型第8层迁移学习保存的最优输出权重作为最终的权重。

为了证明本文提出的分层迁移学习策略能够改善小样本数据情况下的预测误差，分别使用目标域3个月、6个月、9个月的数据量样本，采用以下训练策略进行对比实验，预测误差对比如表5所示。

1) 不迁移：不进行迁移学习，直接进行训练并预测；

2) 直接迁移：采用传统迁移学习进行训练并预测；

3) 分层迁移：采用本文提出的分层迁移学习策略进行训练并预测。

表5展示了在不同数据量下的预测结果，通过对比不同训练策略下的预测误差，本文提出的分层迁移学习策略在3个指标下的表现均最优。以目标域6个月数据为例，相比于直接迁移学习，MAPE指标降低13.31%，MAE指标降低15.16%，RMSE指标降低14.37%。3种不同训练策略的预测曲线对比如图6所示。

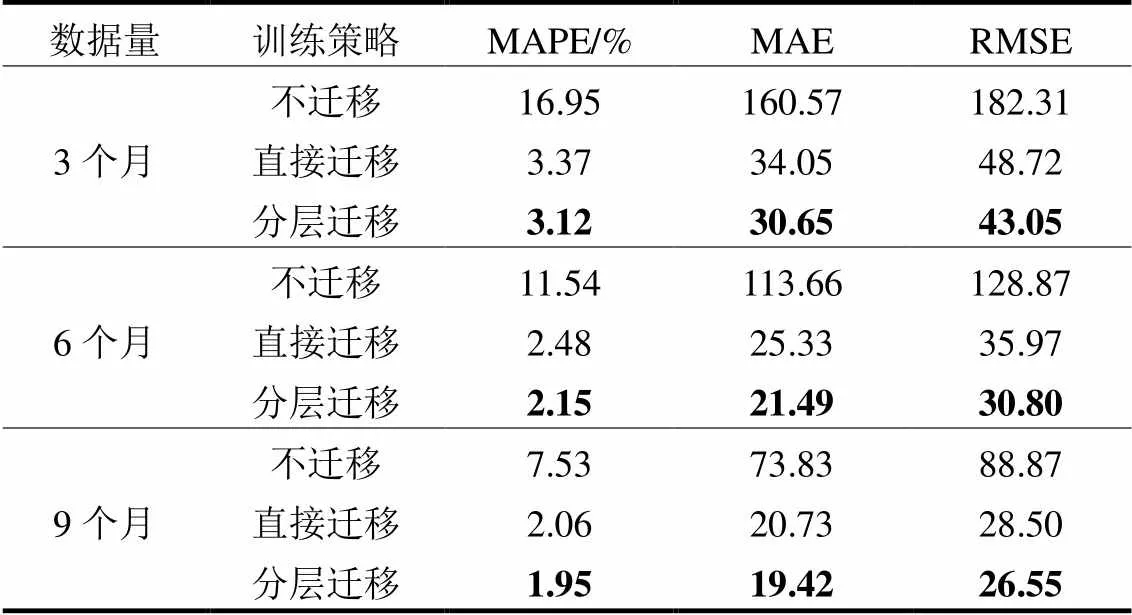
表5 不同训练策略预测结果对比

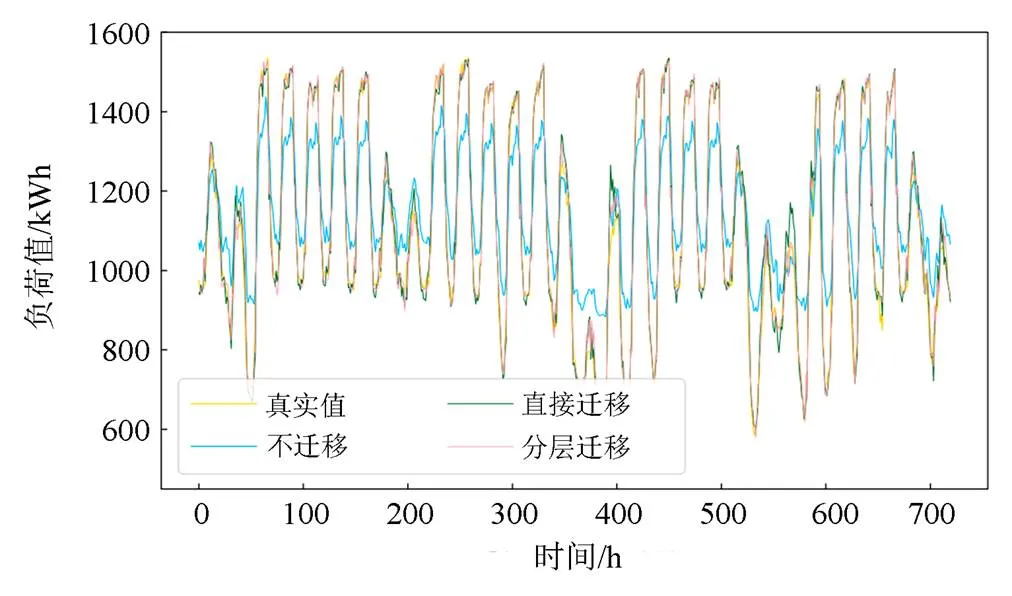
图6 预测曲线对比图

从图6可以看出，本文方法与真实值有最佳的拟合效果，在只有少量训练样本情况下，直接进行初始网络的训练，效果并不理想；采用迁移学习的方式进行训练，在预训练模型基础上，再次采用目标域的数据进行训练，可大幅提升模型收敛的速度，在缺少负荷数据样本的区域建模中，迁移学习具备非常明显的优势。此外，本文提出的分层迁移学习在此基础上进一步优化，通过寻找源域数据和目标域数据的相似数据，不同相似程度的数据输入到基础模型的不同层级分别训练，学习到的负荷周期信息更加丰富，降低了预测误差。

3.4.3多步预测性能

上述实验均为单步预测，为了进一步验证方法的有效性，在3个数据量上保持数据集的划分比例不变，改变模型输入的滑动窗口大小和输出长度，对负荷数据进行多步预测。设定多步预测为预测未来24个时间步的负荷值，即固定输出长度= 24，然后对进行集中调优。保持其余参数不变，预设置为{24,48,72,96,120,144,168}。经过实验分析对比，的大小设置为120时预测效果最佳。因此，在本文的多步预测模型中，滑动窗口大小= 120，输出长度= 24，即利用过去5天(5 ×24 = 120)的负荷数据预测后24个时间步的负荷值。多步预测的输出形式如式(18)所示。

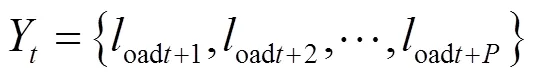
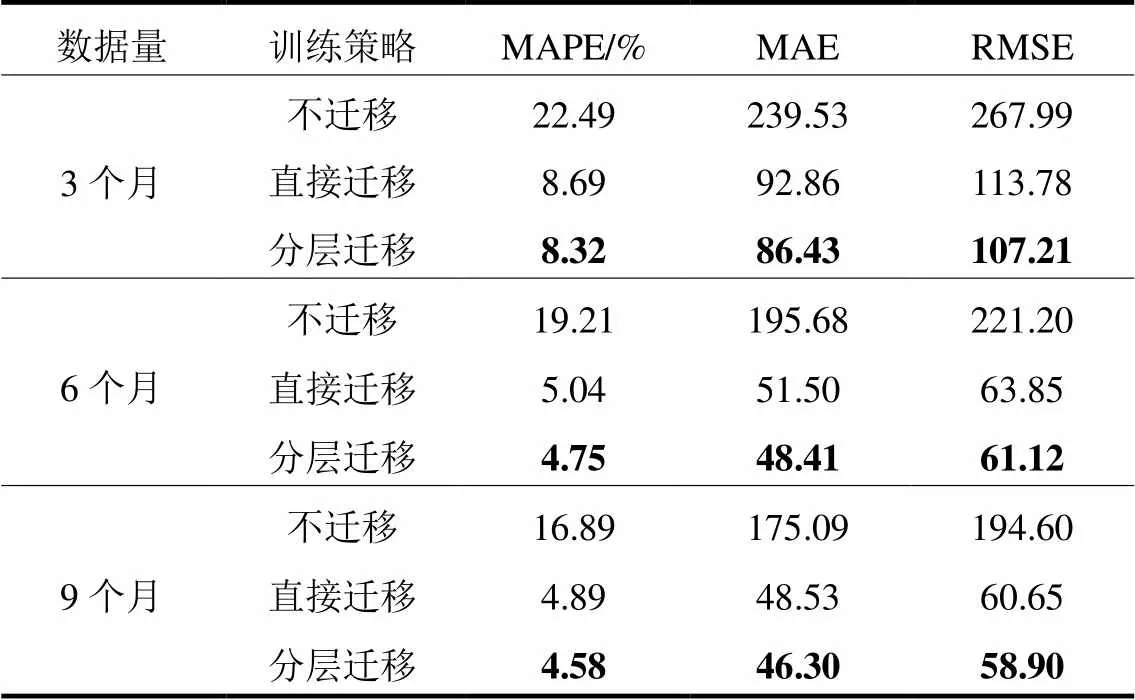
表6 不同训练策略预测误差结果对比

4 结论

本文针对电力负荷数据样本不足导致模型训练不充分从而预测精度不高的问题提出了一种融合分层级迁移学习和多尺度CNN-BiLSTM-Attention的短期电力负荷预测方法。经过实验分析，可以得出如下结论：

1) 多尺度CNN-BiLSTM-Attention模型使用不同大小的卷积核通过串行叠加和并行拼接的方式对特征进行充分学习，利用CNN在提取数据局部特征和BiLSTM在学习时间依赖关系上的优势，并结合注意力机制在处理高噪声、非平稳和非线性数据上表现出优良的性能。

2) 实验对比了在负荷预测中应用较为广泛的ARIMA、LSTM、CNN-LSTM、CNN-GRU、BiLSTM- LSTM、SVR、XGBoost、ELM模型，本文提出的多尺度CNN-BiLSTM-Attention模型取得了较高的精度。

3) 采用分层迁移学习对比不同数据量样本下的实验结果，以目标域6个月数据为例，相比于直接迁移学习，MAPE指标降低13.31%，MAE指标降低15.16%，RMSE指标降低14.37%。在单步预测和多步预测上，本文方法均拥有更好的预测效果，证明了改进的分层迁移学习方法能够有效改善数据样本不足时预测精度不高的情况。

本实验仅在公开的数据集上随机选取了9个区域的负荷数据集进行实验，在未来的工作中，会进一步将分层迁移学习策略细化，对不同类型不同领域的数据进行分析验证，增强分层迁移学习策略的适用范围。

[1] 范士雄, 李立新, 王松岩, 等. 人工智能技术在电网调控中的应用研究[J]. 电网技术, 2020, 44(2): 401-411.

FAN Shixiong, LI Lixin, WANG Songyan, et al. Application analysis and exploration of artificial intelligence technology in power grid dispatch and control[J]. Power System Technology, 2020, 44(2): 401-411.

[2] WU F, CATTANI C, SONG W Q, et al. Fractional ARIMA with an improved cuckoo search optimization for the efficient short-term power load forecasting[J]. AEJ- Alexandria Engineering Journal, 2020, 59(5): 3111-3118.

[3] WANG Y, ZHANG N, CHEN X, et al. A short-term residential load forecasting model based on LSTM recurrent neural network considering weather features[J]. Energies, 2021, 14(10).

[4] 李焱, 贾雅君, 李磊, 等. 基于随机森林算法的短期电力负荷预测[J]. 电力系统保护与控制, 2020, 48(21): 117-124.

LI Yan, JIA Yajun, LI Lei, et al. Short term power load forecasting based on a stochastic forest algorithm[J]. Power System Protection and Control, 2020, 48(21): 117-124.

[5] WU J R, WANG G W, TIAN Y C, et al. Support vector regression with asymmetric loss for optimal electric load forecasting[J]. Energy, 2021, 223.

[6] 姜建, 刘海琼, 李衡, 等. 基于XGBoost的配电网线路峰值负荷预测方法[J]. 电力系统保护与控制, 2021, 49(16): 119-127.

JIANG Jian, LIU Haiqiong, LI Heng, et al. Peak load forecasting method of distribution network lines based on XGBoost[J]. Power System Protection and Control, 2021, 49(16): 119-127.

[7] 侯慧, 王晴, 赵波, 等. 关键信息缺失下基于相空间重构及机器学习的电力负荷预测[J]. 电力系统保护与控制, 2022, 50(4): 75-82.

HOU Hui, WANG Qing, ZHAO Bo, et al. Power load forecasting without key information based on phase space reconstruction and machine learning[J]. Power System Protection and Control, 2022, 50(4): 75-82.

[8] HU Y, QU BY, WANG J, et al. Short-term load forecasting using multimodal evolutionary algorithm and random vector functional link network based ensemble learning[J]. Applied Energy, 2021, 285.

[9] KIM J, MOON J, HWANG E, et al. Recurrent inception convolution neural network for multi short-term load forecasting[J]. Energy and Buildings, 2019, 194: 328-341.

[10] WEN Lulu, ZHOU Kaile, YANG Shanlin, et al. Optimal load dispatch of community microgrid with deep learning based solar power and load forecasting[J]. Energy, 2019, 171: 1053-1065.

[11] 李丹, 张远航, 杨保华, 等. 基于约束并行LSTM分位数回归的短期电力负荷概率预测方法[J]. 电网技术, 2021, 45(4): 1356-1364.

LI Dan, ZHANG Yuanhang, YANG Baohua, et al. Short time power load probabilistic forecasting based on constrained parallel-LSTM neural network quantile regression mode[J]. Power System Technology, 2021, 45(4): 1356-1364.

[12] 王凌云, 林跃涵, 童华敏, 等. 基于改进Apriori关联分析及MFOLSTM算法的短期负荷预测[J]. 电力系统保护与控制, 2021, 49(20): 74-81.

WANG Lingyun, LIN Yuehan, TONG Huamin, et al. Short-term load forecasting based on improved Apriori correlation analysis and an MFOLSTM algorithm[J]. Power System Protection and Control, 2021, 49(20): 74-81.

[13] 杨龙, 吴红斌, 丁明, 等. 新能源电网中考虑特征选择的Bi-LSTM网络短期负荷预测[J]. 电力系统自动化, 2021, 45(3): 166-173.

YANG Long, WU Hongbin, DING Ming, et al. Short- term load forecasting in renewable energy grid based on bi-directional long short-term memory network considering feature selection[J]. Automation of Electric Power Systems, 2021, 45(3): 166-173.

[14] YANG M, WANG J. Adaptability of financial timeseries prediction based on BiLSTM[J]. Procedia Computer Science, 2022, 199: 18-25.

[15] SIAMI-NAMINI S, TAVAKOLI N, NAMIN A S. The performance of LSTM and BiLSTM in forecasting time series[C] // IEEE International Conference on Big Data (Big Data), December 9-12, 2019, Los Angeles, CA, USA: 3285-3292.

[16] VEERAMSETTY V, REDDY KR, SANTHOSH M, et al. Short-term electric power load forecasting using random forest and gated recurrent unit[J]. Electrical Engineering, 2022, 104(1): 307-329.

[17] RIBEIRO MHD, COELHO LD. Ensemble approach based on bagging, boosting, and stacking for short-term prediction in agribusiness time series[J]. Applied Soft Computing, 2020, 86.

[18] 朱凌建, 荀子涵, 王裕鑫, 等. 基于CNN-BiLSTM的短期电力负荷预测[J]. 电网技术, 2021, 45(11): 4532-4539.

ZHU Lingjian, XUN Zihan, WANG Yuxin, et al. Short-term power load forecasting based on CNN-BiLSTM[J]. Power System Technology, 2021, 45(11): 4532-4539.

[19] JIN X B, ZHENG W Z, KONG J L, et al. Deep-learning forecasting method for electric power load via attention- based encoder-decoder with Bayesian optimization[J]. Energies, 2021, 14(6).

[20] SUTSKEVER I, VINYALS O, Le Q V. Sequence to sequence learning with neural networks[C] // 28th Annual Conference on Neural Information Processing Systems, December 8-13, 2014: 3104-3112.

[21] 魏健, 赵红涛, 刘敦楠, 等. 基于注意力机制的CNN-LSTM 短期电力负荷预测方法[J]. 华北电力大学学报, 2021, 48(1): 42-47.

WEI Jian, ZHAO Hongtao, LIU Dunnan, et al. Short-term power load forecasting method by attention-based CNN- LSTM[J]. Journal of North China Electric Power University, 2021, 48(1): 42-47.

[22] 任建吉, 位慧慧, 邹卓霖, 等. 基于CNN-BiLSTM- Attention的超短期电力负荷预测[J]. 电力系统保护与控制, 2022, 50(8): 108-116.

REN Jianji, WEI Huihui, ZOU Zhuolin, et al. Ultra-short- term power load forecasting based on CNN-BiLSTM- Attention[J]. Power System Protection and Control, 2022, 50(8): 108-116.

[23] WANG Weiping, WANG Zhaorong, ZHOU Zhanfan, et al. Anomaly detection of industrial control systems based on transfer learning[J]. Tsinghua Science and Technology, 2021, 26(6): 821-832.

[24] KUMAR P, HATI A S. Transfer learning-based deep CNN model for multiple faults detection in SCIM[J]. Neural Computing and Applications, 2021, 33: 15851-15862.

Short-term power load forecasting method based on improved hierarchical transfer learning and multi-scale CNN-BiLSTM-Attention

OUYANG Fulian, WANG Jun, ZHOU Hangxia

(College of Information Engineering, China Jiliang University, Hangzhou 310018, China)

Insufficient power load data samples in the target domain result in inadequate model training and low prediction accuracy. Thus an improved hierarchical transfer learning strategy combined with a multi-scale CNN-BiLSTM-Attention model is proposed for short-term power load forecasting. A multi-scale CNN superimposed, linked and in parallel is designed as a feature extractor, and the features are then passed as input to two BiLSTM structures for further learning. Then an attention mechanism is introduced to adjust the weight of the captured information vector. This paper divides the layers according to the structure of the basic model, and inputs the source data into the model according to the level of the goodness-of-fit value to perform hierarchical transfer learning training. It then retains the optimal training weight of each layer, and uses the target domain data to carry out model training and obtain the final predictive model after fine-tuning. Experiments show that the proposed multi-scale CNN-BiLSTM-Attention model can effectively improve the accuracy of load prediction. When the load data samples are insufficient, the improved hierarchical transfer learning strategy can effectively reduce the prediction error compared with traditional transfer learning. Taking six months of data in the target domain as an example, compared with traditional transfer learning, the MAPE is reduced by 13.31%, MAE is reduced by 15.16%, and RMSE is reduced by 14.37%.

power load forecasting; CNN; BiLSTM; attention mechanism; transfer learning

10.19783/j.cnki.pspc.220422

浙江省基础公益研究计划项目资助(LGG22E070003)

This work is supported by the Basic Public Welfare Research Program of Zhejiang Province (No. LGG22E070003).

2022-03-26；

2022-06-02

欧阳福莲(1998—)，女，硕士研究生，研究方向为智能电网、深度学习；E-mail: P20030854058@cjlu.edu.cn

王 俊(1998—)，男，硕士研究生，研究方向为时间序列分析、智能算法；E-mail: S20030812009@cjlu.edu.cn

周杭霞(1963—)，女，通信作者，教授，硕士生导师，研究方向为智慧能源、模式识别与数据挖掘。E-mail: zhx@ cjlu.edu.cn

(编辑 魏小丽)