适应非光滑特性的交直流混合电力系统状态估计

巨云涛，黄 炎

适应非光滑特性的交直流混合电力系统状态估计

巨云涛，黄 炎

(中国农业大学信息与电气工程学院，北京 100083)

交直流混合电力系统中的有载调压变压器(on-load-tap-changer, OLTC)和换流器模型存在大量限幅、死区等非光滑特性，如何处理换流器引入的分段函数约束是当前状态估计的研究难点。构建了OLTC的混合整数非线性(mixed integer nonlinear programming, MINLP)模型，通过控制二次侧电压水平得到OLTC挡位的估计值。针对换流器采用分段函数描述包含限幅、死区等下垂控制特性的问题，提出采用近似拟合函数将分段函数光滑化。与采用MINLP描述分段函数的方法相比，所提模型显著提高了计算效率。通过3节点和IEEE14节点交直流混合系统算例，验证了所提状态估计模型的正确性和实用性，同时分析了拟合系数对状态估计的影响。算例表明，所提模型增强了状态估计处理不良数据的能力，提高了对非光滑特性的适应能力，在保证计算精度的前提下能够提高状态估计的收敛性。

交直流混合；换流器；有载调压变压器；非光滑特性

0 引言

状态估计(state estimation, SE)是实现电力系统安全评估、实时调度和稳定运行的基础[1-3]。在“碳达峰，碳中和”的目标背景下，电网的新能源接入比例越来越高，电力系统电力电子化程度增高，状态估计中考虑有载调压变压器(on-load-tap-changer, OLTC)、电力电子设备会引入大量含离散变量的限幅、死区等非光滑约束，国内外关于此类非光滑约束的研究尚不多见[4-6]。

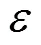
基于物理模型的传统SE方法仍是当前能量管理系统(energy management system, EMS)的主流方法。现有文献多集中研究SE中的坏数据处理，以及如何提高SE的精度和计算效率，较少文献给出SE中电力系统OLTC、换流器等元件的详细物理建模过程[14-16]。文献[17]提出了基于等值信息交换的分布式抗差状态估计算法，在保护区域隐私的前提下极大地提高了计算效率。文献[18]提出采用三阶段的方法过滤量测生数据进而提高SE精度，并详细给出了基于序分量模型的三相分布式电源建模过程。文献[19]构建了交直流混合系统的SE模型，给出了AC/DC、DC/DC 系统中2种换流器的物理模型，但没有考虑换流器的下垂控制特性。换流器[20]通常建模成“变压器+滤波器+移相器+逆变器”的组合模型[21-23]。一般有以下4种控制方式：(1) 交流母线有功功率、无功功率恒定；(2) 交流母线有功功率、电压幅值恒定；(3) 直流电压、交流母线无功功率恒定；(4) 直流电压、交流母线电压幅值恒定。此外，文献[24]提出包含无功功率限幅的Q-V下垂控制，即控制交流母线有功功率恒定，交流母线无功功率和电压幅值满足下垂控制函数。文献[25]提出了包含直流侧有功功率限幅的下垂控制，即控制交流母线无功功率恒定，直流侧有功功率和电压幅值满足下垂控制函数，但没有考虑死区。

下垂控制函数是一个分段函数，具有严重非光滑特性，当系统运行至拐点附近时，导数不连续，容易导致算法计算失败。对于分段函数所描述的问题，常用的方法是采用混合整数非线性规划(mixed integer nonlinear programming, MINLP)。文献[26-27]提出采用混合整数非线性规划方法进行处理，但增加了0-1整数变量，使得计算效率大大降低。文献[28]从建模的角度处理了分段函数，提出了一种分段线性函数进行拟合，并通过投影信赖域法进行了有效计算，但分段线性函数仍然是分段函数，具有强非光滑特性，对算法收敛域的要求较高。

因此，为了更加详细地将OLTC、换流器模型纳入现有EMS的SE程序中，在SE建模方面提出以下改进：

1) 考虑有载调压变压器的控制特性，给出OLTC的详细建模过程，建立基于MINLP方法的OLTC状态估计模型；

2) 考虑换流器模型中包含的限幅、死区等非光滑特性，采用拟合函数近似处理换流器分段下垂控制函数，建立换流器的光滑化模型，分析拟合系数对SE的影响。

所提模型增强了SE对坏数据以及非光滑约束的处理能力，提高了适应非光滑特性的交直流混合电力系统状态估计性能。

1 最小二乘状态估计

1.1 目标函数

当前EMS能量管理系统中主要采用最小二乘状态估计[29]。

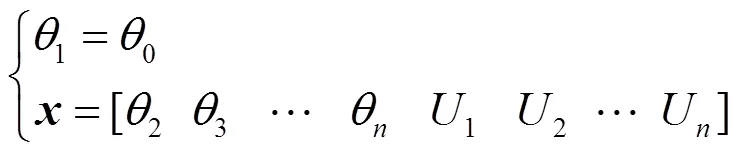
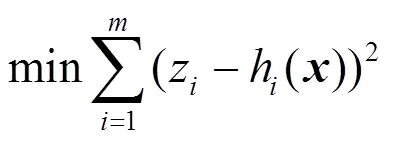
1.2 量测方程

图1 线路等效模型

节点电压幅值的量测方程为

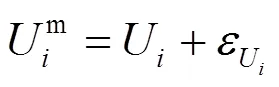
节点注入功率的量测方程为

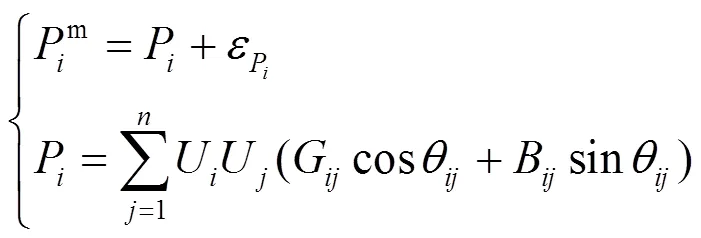
支路功率的量测方程为

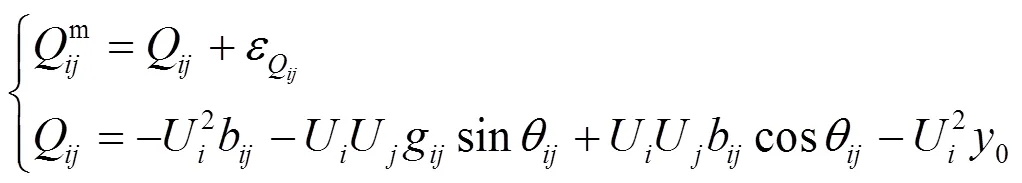
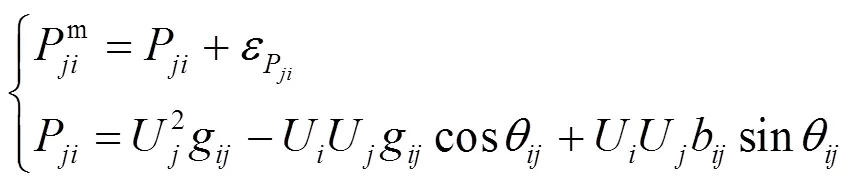
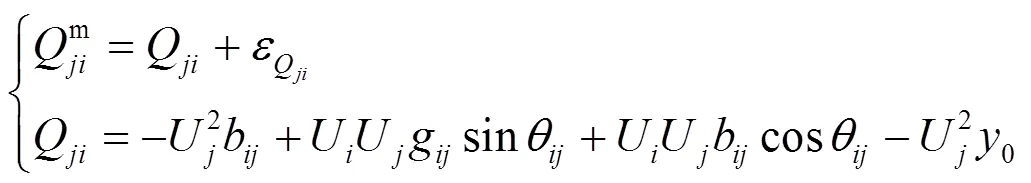
1.3 零注入等式约束条件

最小二乘状态估计的等式约束包括零注入有功功率和无功功率约束，可表示为

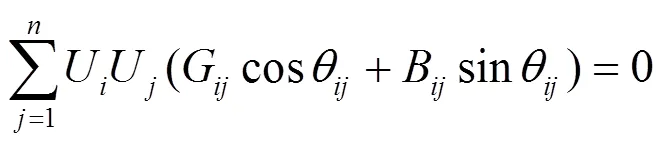
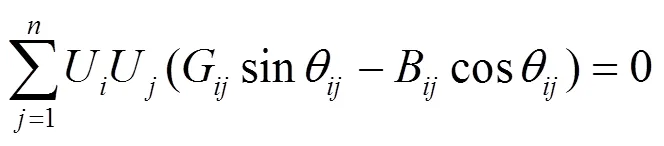
式(11)、式(12)的物理意义是流入或流出零注入功率节点的有功、无功功率之和为0。

1.4 不等式约束条件

本文考虑功率及电压幅值的限幅不等式约束，如式(13)所示。

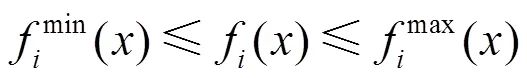
支路传输功率的数学表达式为

2 有载调压变压器MINLP模型

图2 有载调压变压器模型

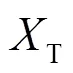
式中：表示有载调压变压器的无功功率损耗；为额定变比；为分接头的分级步长；为二次侧电压控制目标；为电压带宽；表示分接头挡位取值，是离散变量；、分别表示挡位的上、下限。

3 换流器光滑化模型

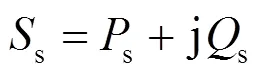
图4 换流器等效电路图

交流区域的零注入等式约束可表示为

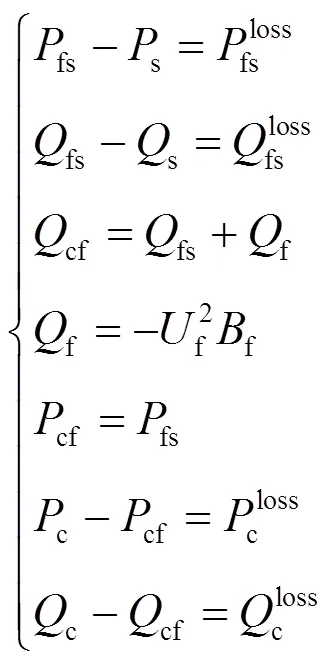
直流区域的零注入等式约束为

图5 特性曲线

分段函数表达式为

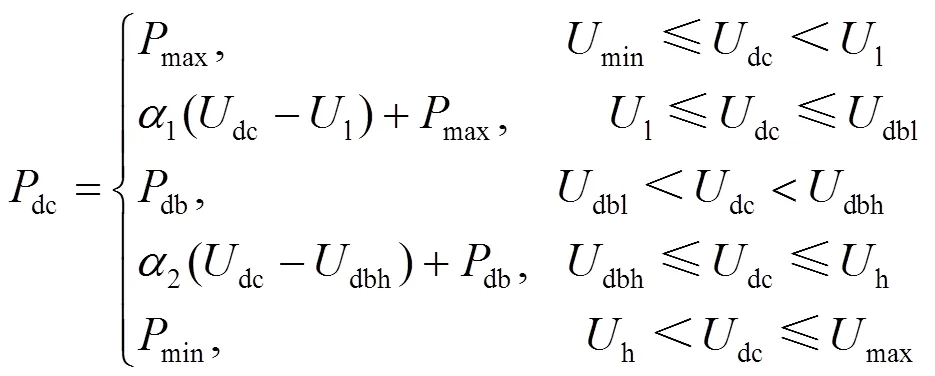
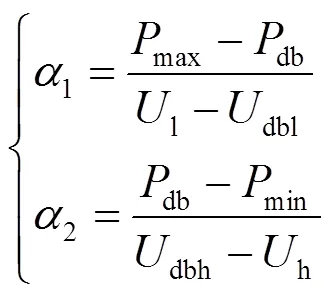
通常采用混合整数非线性规划描述分段函数控制特性，但该方法计算效率较低。本文采用拟合函数对分段函数进行近似拟合，拟合后的下垂控制函数为

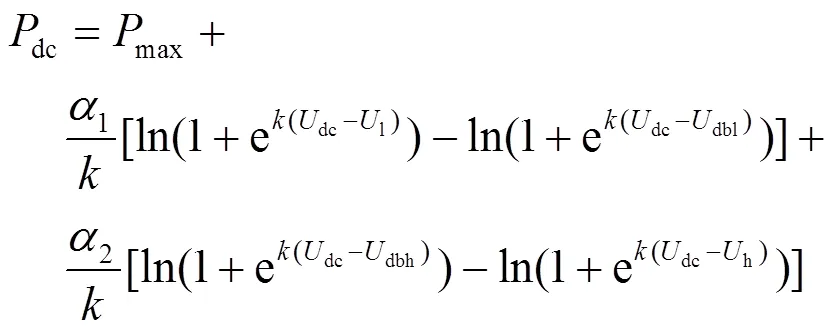
对分段函数的近似拟合，可使其转换成处处可导且导数连续的光滑化函数，如图6所示。光滑化函数可以在算法迭代计算的过程中避免导数阶跃变化，提高了算法的收敛性。

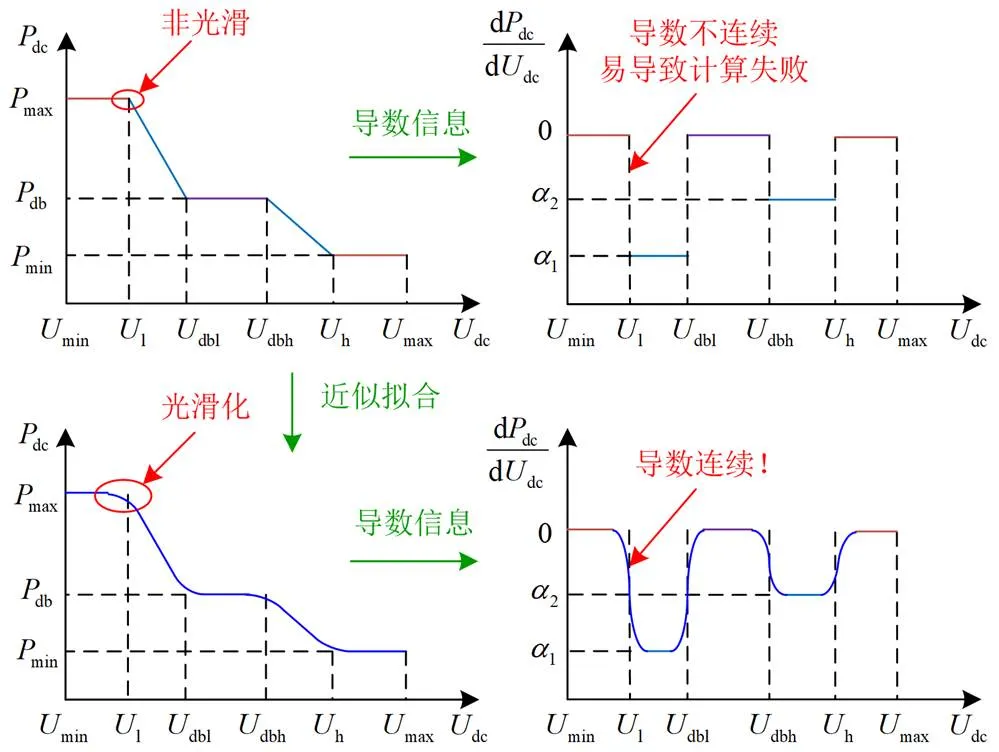
图6 拟合前后导数对比图

4 算例分析

为了验证本文所提出的状态估计模型的正确性与实用性，本文采用3节点和IEEE14节点系统对所提模型进行测试。在考虑量测坏数据和量测误差的情况下，分别对比采用有载调压变压器MINLP模型、换流器光滑化模型得到估计值与真值之间的误差，并进行定量分析。为便于分析，本文选取均方根误差(root mean squared error, RMSE)和最大绝对误差(maximum absolute error, MAE)两个数学指标。均方根误差在本文中表示状态变量估计值与真值之间误差的平方和与节点个数的比值的平方根；最大绝对误差一般用来衡量绝对误差的范围，即状态变量估计值与真值之间绝对误差的最大值，两个指标的数学表达为

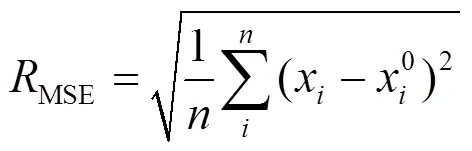
算例系统量测值采用系统潮流解加上正态分布量测误差模拟，均值为0，方差为0.000 005，且采用标幺值计算，基准容量和基准电压分别为100 MVA、110 kV。本文采用GAMS优化软件[30]，版本为24.7，调用Knitro求解器[31]计算。测试系统的硬件环境为英特尔 i7-8550U CPU 1.80 GHz，16.0 GB内存，操作系统为Win10 64 bit专业版。

4.1 3节点系统

图7 3节点系统结构示意图

表1 3节点系统量测配置

表2 3节点系统电压幅值量测值(含坏数据)

采用第2节介绍的有载调压变压器MINLP模型进行测试计算，分析模型的计算精度。

状态变量及分接头挡位的估计值与真值对比如图8、表3和表4所示。

图8 3节点系统节点电压幅值估计值对比

表3 状态变量及分接头挡位的估计值与真值对比

表4 电压幅值计算精度分析

图8、表3和表4中的“MINLP模型”表示采用第2节介绍的OLTC模型计算得到的估计值。结果表明，对于3节点系统，当状态估计存在坏数据和量测误差时，采用MINLP模型计算得到的估计值与真值一致，证明模型具有较高的估计精度。

4.2 IEEE14节点系统

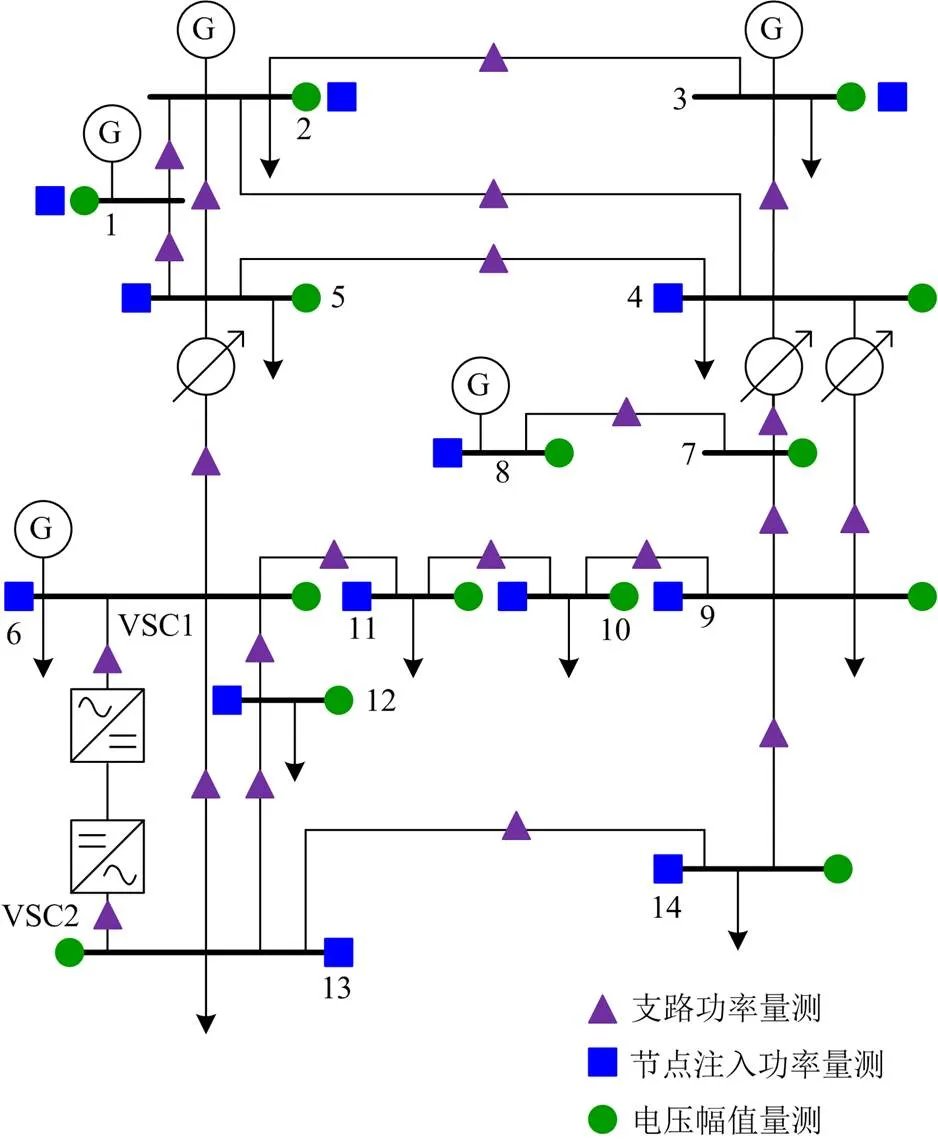
图9 IEEE14节点系统结构示意图

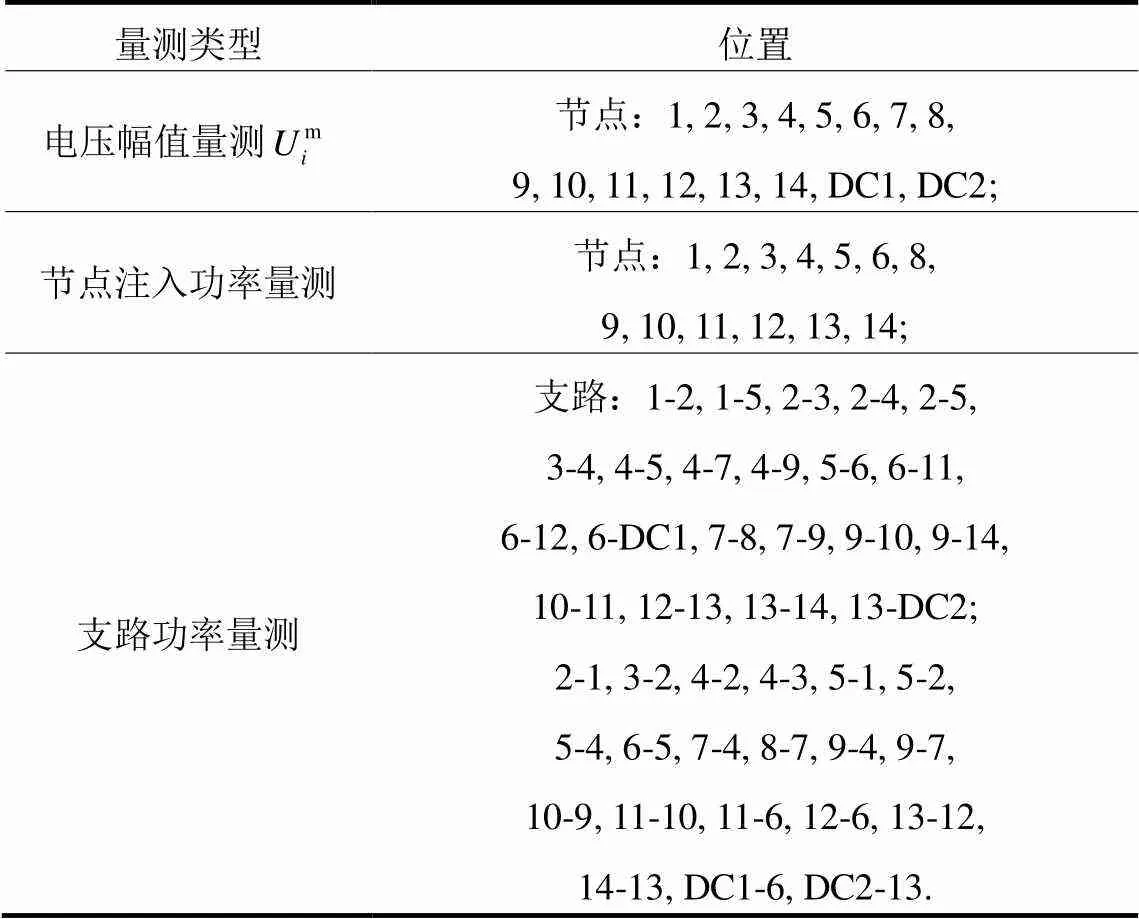
表5 IEEE14节点系统量测配置

采用拟合函数对分段函数进行近似拟合，取拟合系数，对比拟合前后的下垂控制特性曲线，如图10所示。

为了进一步验证所提状态估计模型的正确性与有效性，考虑系统中存在坏数据进行下一步测试，坏数据信息如表6所示。

表6 IEEE14节点系统部分量测信息(含坏数据)

对OLTC二次侧电压增加控制范围，同时对系统中的部分变量增加限幅不等式约束，详细信息见表7。

表7 IEEE14节点系统考虑的不等式约束

4.2.1计算精度分析

对本文所提出的有载调压变压器MINLP模型及换流器光滑化模型进行状态估计测试，分析模型的计算精度。在有载调压器变压器采用MINLP模型的情况下，对换流器的两种建模方法进行对比分析。

方法1：采用本文提出的光滑化模型。

方法2：采用MINLP模型描述分段函数特性。

计算结果对比如图11、图12和表8所示。

由图11和表8可知，对于IEEE14节点系统，当系统中存在坏数据和量测误差时，估计结果与真值会存在一定偏差，不等式约束的限幅环节可增强对坏数据的处理能力，保证估计结果的合理性。此外，采用本文提出模型得到的估计值与采用换流器MINLP模型得到的结果一致，可进一步验证本文所提光滑化模型的精确性。

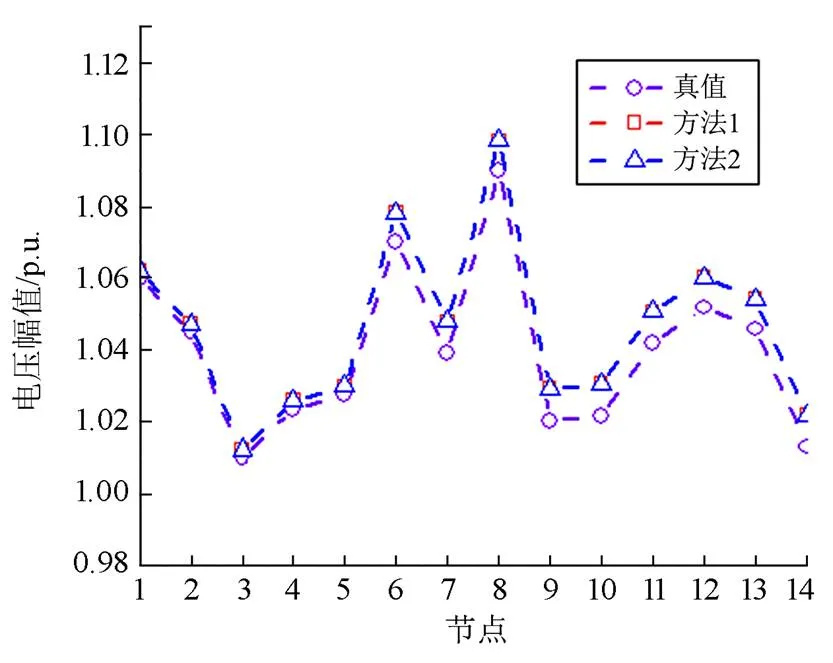
图11 IEEE14节点系统电压幅值与分接头挡位估计值对比

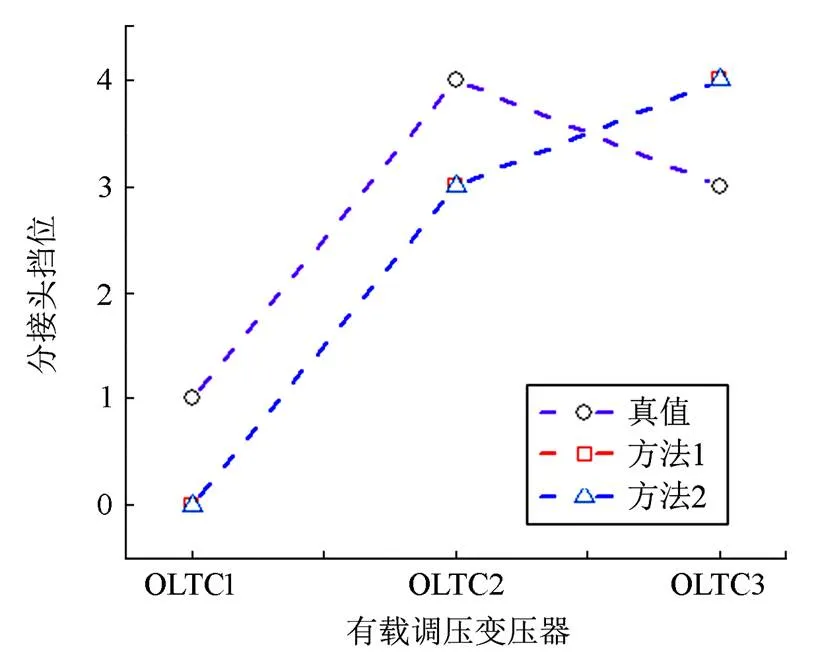
图12 IEEE14节点系统分接头挡位估计值对比

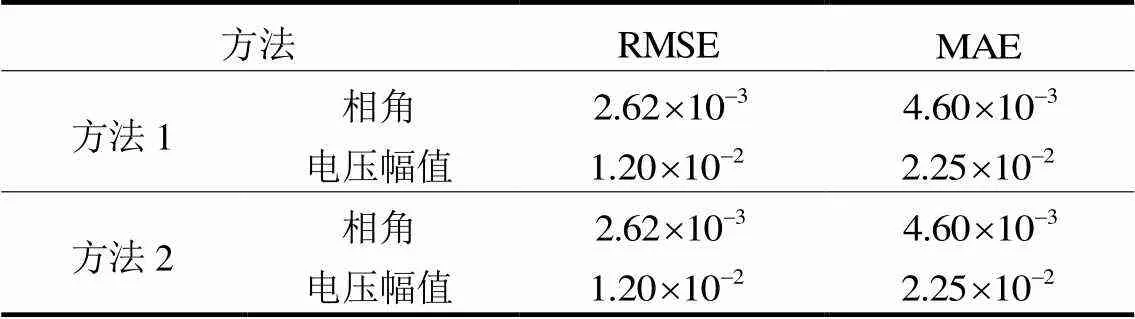
表8 节点电压计算精度分析

4.2.2计算效率分析

为验证本文所提换流器光滑化模型在计算效率上的优势，对比分析采用不同求解器求解不同方法所需要的CPU耗时。Knitro、SBB[32]和Bonmin[33]3个求解器计算所需的CPU耗时如表9所示。

表9 不同求解器计算所需CPU耗时

综合图11、图12、表8与表9的结果可以得到，对于IEEE14节点测试系统，本文所提光滑化模型测试得到的结果与换流器MINLP模型测试结果相同，但对于3种不同的求解器，本文所提模型计算所需CPU耗时均小于换流器MINLP模型。其中Knitro求解器求解光滑化模型仅需0.602 s，相比于换流器MINLP模型，其计算效率提高了近6倍，这在工程应用中至关重要。算例结果验证本文所提换流器光滑化模型计算效率更高，能够较好地满足现场对状态估计实时性的需求。

4.2.3拟合系数的影响分析

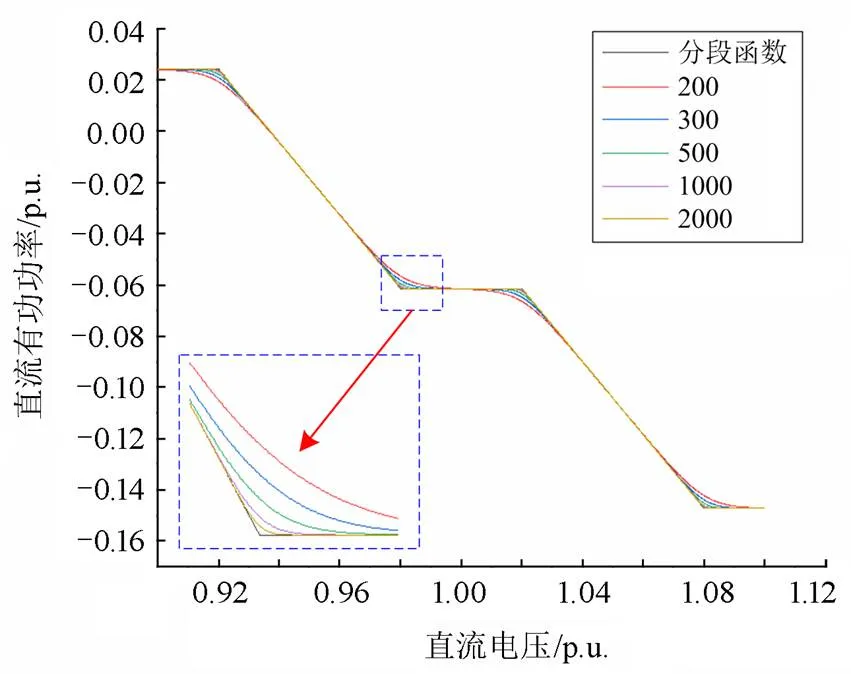
图13 拟合系数对近似拟合的影响

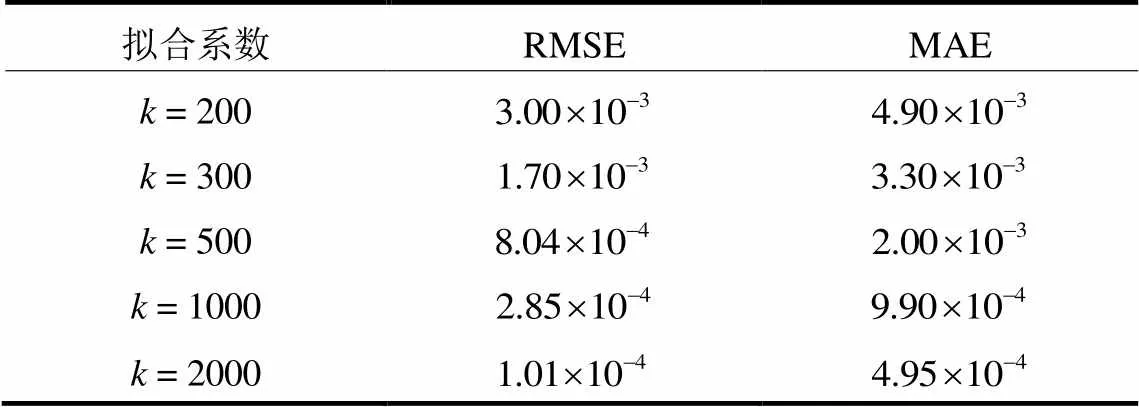
表10 拟合精度分析

由图13与表10可知，当拟合系数取= 200、= 300时，拟合曲线与原曲线误差较大，拟合精度较低。随着拟合系数的增大，拟合曲线与原曲线的拟合精度越来越高，但拟合系数过大会对状态估计精度和计算效率产生不利影响。下文从状态估计的计算效率和目标函数优化结果的角度对比不同拟合系数的区别。

表11 计算效率及目标函数结果分析

表11中的“目标函数”即为估计值与真值的残差平方和，目标函数越小表示估计结果越精确。由表11可知，随着拟合系数的增大，Bonmin求解器的估计精度会降低。同时，随着拟合系数的增加，求解器所需的CPU耗时均有不同程度地增加，这不利于实现状态估计的实时性。而且由于拟合函数中存在自然底数e的指数函数，其特点是函数值会随着自变量的增加而呈现爆炸式增长，当拟合系数继续增大至= 6000时，会达到GAMS优化软件的存储极限导致状态估计无法计算。

综上，对于本文算例系统参数，= 500足以在满足精度要求的前提下拥有较高的求解效率，是精确性与快速性的折衷选择。需要指出的是，对于不同的算例参数，拟合系数的选择并不是唯一的，应根据下垂曲线的参数，兼顾计算效率与计算精度进行合理选择。

5 结论

现有EMS状态估计对交直流混合电力系统中的换流器分段函数约束适应性差。本文考虑状态估计中OLTC、换流器的详细物理特性，构建了OLTC的MINLP模型和计及限幅、死区特性的换流器光滑化模型，增强了对坏数据的处理能力。文中提出采用数学拟合的方法近似处理换流器的下垂控制函数，实现分段函数连续光滑化。算例结果表明，在OLTC采用MINLP模型的基础上，对换流器下垂控制函数进行拟合，可以提高状态估计收敛性，在保证计算精度的前提下极大地提高了状态估计的计算效率。此外，拟合系数的取值不同会对状态估计的计算精度和计算效率产生影响，应根据实际算例系统合理选择。后续工作将围绕系统中的三相不平衡特性展开，构建适应非光滑特性的三相交直流混合电力系统状态估计模型。

[1] 陈艳波, 于尔铿. 电力系统状态估计[M]. 北京: 科学出版社, 2021.

[2] EXPÓSITO A A, ANTONIO G. Power system state estimation[M]. CRC Press, 2004.

[3] 肖飞, 叶康, 邓祥力, 等. 基于最优编码集及智能状态估计的电网故障诊断方法[J]. 电力系统保护与控制, 2021, 49(2): 89-97.

XIAO Fei, YE Kang, DENG Xiangli, et al. A fault diagnosis method of a power grid based on an optimal coding set and intelligent state estimation[J]. Power System Protection and Control, 2021, 49(2): 89-97.

[4] 李欣悦, 李凤婷, 尹纯亚, 等. 直流双极闭锁故障下送端系统暂态过电压计算方法[J]. 电力系统保护与控制, 2021, 49(1): 1-8.

LI Xinyue, LI Fengting, YIN Chunya, et al. Transient overvoltage calculation method of HVDC sending-end system under DC bipolar blocking[J]. Power System Protection and Control, 2021, 49(1): 1-8.

[5] 张伟晨, 熊永新, 李程昊, 等. 基于改进VDCOL的多馈入直流系统连续换相失败抑制及协调恢复[J]. 电力系统保护与控制, 2020, 48(13): 63-72.

ZHANG Weichen, XIONG Yongxin, LI Chenghao, et al. Continuous commutation failure suppression and coordinated recovery of multi-infeed DC system based on improved VDCOL[J]. Power System Protection and Control, 2020, 48(13): 63-72.

[6] CHEN Y, YAO Y, ZHANG Y. A robust state estimation method based on SOCP for integrated electricity-heat system[J]. IEEE Transactions on Smart Grid, 2021, 12(1): 810-820.

[7] PRIMADIANTO A, LU C N. A review on distribution system state estimation[J]. IEEE Transactions on Power Systems, 2017, 32(5): 3875-3883.

[8] SIDDIQUI A S, PRASHANT. Optimal location and sizing of conglomerate DG-FACTS using an artificial neural network and heuristic probability distribution methodology for modern power system operations[J]. Protection and Control of Modern Power Systems, 2022, 7(1): 124-148.

[9] WENG Y, NEGI R, ILIC M D. Probabilistic joint state estimation for operational planning[J]. IEEE Transactions on Smart Grid, 2019, 10(1): 601-612.

[10] YU J, WENG Y, RAJAGOPAL R. PaToPaEM: a data-driven parameter and topology joint estimation framework for time-varying system in distribution grids[J]. IEEE Transactions on Power Systems, 2019, 34(3): 1682-1692.

[11] 俞文帅, 张晓华, 卫志农, 等. 基于深度神经网络的电力系统快速状态估计[J]. 电网技术, 2021, 45(7): 2551-2561.

YU Wenshuai, ZHANG Xiaohua, WEI Zhinong, et al. Fast state estimation for power system based on deep neural network[J]. Power System Technology, 2021, 45(7): 2551-2561.

[12] ZAMZAM A S, FU X, SIDIROPOULOS N D. Data-driven learning-based optimization for distribution system state estimation[J]. IEEE Transactions on Power Systems, 2019, 34(6): 4796-4805.

[13] 张越, 单连飞, 余建明, 等. 基于ε-模糊树方法的电力系统状态估计[J]. 电力系统保护与控制, 2019, 47(5): 138-144.

ZHANG Yue, SHAN Lianfei, YU Jianming, et al. Power system state estimation based on ε-fuzzy tree method[J]. Power System Protection and Control, 2019, 47(5): 138-144.

[14] 巨云涛, 吴文传, 张伯明. 支持大规模电流量测的配网抗差状态估计方法[J]. 中国电机工程学报, 2011, 31(19): 82-89.

JU Yuntao, WU Wenchuan, ZHANG Boming. A new method for distribution state estimation accommodating current measurements[J]. Proceedings of the CSEE, 2011, 31(19): 82-89.

[15] CHENG Z, REN H, ZHANG B, et al. Distributed kalman filter for large-scale power systems with state inequality constraints[J]. IEEE Transactions on Industrial Electronics, 2021, 68(7): 6238-6247.

[16] CHAKHCHOUKH Y, ISHII H. Enhancing robustness to cyber-attacks in power systems through multiple least trimmed squares state estimations[J]. IEEE Transactions on Power Systems, 2016, 31(6): 4395-4405.

[17] 王帅, 张海波. 基于等值信息交换的分布式抗差估计算法[J]. 电力系统保护与控制, 2021, 49(15): 30-37.

WANG Shuai, ZHANG Haibo. A distributed robust estimation algorithm based on equivalent information exchange[J]. Power System Protection and Control, 2021, 49(15): 30-37.

[18] 巨云涛, 于燕玲, 吴文传, 等. 三阶段式交直流混合主动配电网三相区间状态估计[J]. 高电压技术, 2021, 47(7): 2330-2341.

JU Yuntao, YU Yanling, WU Wenchuan, et al. Three-phase interval state estimation for three-stage AC-DC hybrid active distribution network[J]. High Voltage Engeering, 2021, 47(7): 2330-2341.

[19] FANG Z, LIN Y, SONG S, et al. A comprehensive framework for robust AC/DC grid state estimation against measurement and control input errors[J]. IEEE Transactions on Power Systems, 2022, 37(2): 1067-1077.

[20] XING G, MIN Y, CHEN L, et al. Limit induced bifurcation of grid-connected VSC caused by current limit[J]. IEEE Transactions on Power Systems, 2021, 36(3): 2717-2720.

[21] BEERTEN J, COLE S, BELMANS R. Generalized steady-state VSC MTDC model for sequential AC/DC power flow algorithms[J]. IEEE Transactions on Power Systems, 2012, 27(2): 821-829.

[22] MARTÍNEZ-PARRALES R, FUERTE-ESQUIVEL C R. A new unified approach for the state estimation and bad data analysis of electric power transmission systems with multi-terminal VSC-based HVDC networks[J]. Electric Power Systems Research, 2018, 160: 251-260.

[23] ACHA E, CASTRO L M. A generalized frame of reference for the incorporation of multi-terminal VSC-HVDC systems in power flow solutions[J]. Electric Power Systems Research, 2016, 136: 415-424.

[24] KIM J, SEOK J K, MULJADI E, et al. Adaptive Q–V scheme for the voltage control of a DFIG-Based wind power plant[J]. IEEE Transactions on Power Electronics, 2016, 31(5): 3586-3599.

[25] LI B, LI Q, WANG Y, et al. A novel method to determine droop coefficients of DC voltage control for VSC-MTDC system[J]. IEEE Transactions on Power Delivery, 2020, 35(5): 2196-2211.

[26] DAKIN R J. A tree-search algorithm for mixed integer programming problems[J]. Computer Journal, 1965, 8(3): 250-255.

[27] CHAMBERS M L, HILLIER F S, LIEBERMAN G J. Introduction to operations research[J]. Series A (General), 1976, 139(2): 273.

[28] JU Y, WANG J, ZHANG Z. An improved power flow method to cope with non-smooth constraints of integrated energy systems[J]. CSEE Journal of Power and Energy Systems, 2020, 7: 1-10.

[29] RAMOS C J, MARTINS A P, CARVALHO A S. Frequency and phase-angle estimation using ordinary least squares[J]. IEEE Transactions on Industrial Electronics, 2015, 62(9): 5677-5688.

[30] RICHARD E R. GAMS-a user's guide[R]. Washington: GAMS Development Corporation, 2014.

[31] YUMPU.COM. KNITRO user's manual version 5.0- Ziena Optimization Inc[EB/OL].[2021-12-02]. https:// www.yumpu.com/en/document/view/37639221/knitro-users-manual-version-50-ziena-optimization-inc.

[32] GUPTA O K, RAVINDRAN A. Branch and bound experiments in convex nonlinear integer programming[J]. Management Science, 1985, 31(12): 1533-1546.

[33] BONAMI P, GONÇALVES J P M. Heuristics for convex mixed integer nonlinear programs[J]. Computational Optimization and Applications, 2012, 51(2): 729-747.

State estimation for an AC/DC hybrid power system adapted to non-smooth characteristics

JU Yuntao, HUANG Yan

(College of Information and Electrical Engineering, China Agricultural University, Beijing 100083, China)

In an AC/DC hybrid power system, converter and on-load-tap-changer (OLTC) models have a large number of non-smooth characteristics such as limits and a dead zone. How to deal with the piecewise function constraints introduced by a converter is a difficult problem in existing state estimation. A mixed integer nonlinear programming (MINLP) model of OLTC is proposed and tap position is estimated by controlling the secondary voltage level. Given that the converter uses piecewise functions to describe droop control characteristics including limits, dead zone and so on, the piecewise functions are smoothed by approximate fitting functions. The proposed model significantly improves the computational efficiency compared with the method of using MINLP to describe piecewise functions. The correctness and practicability of the proposed SE model are verified on a 3-bus system and IEEE14-bus AC/DC hybrid systems, and the influence of the fitting coefficient on state estimation is analyzed. Numerical examples show that the proposed model can enhance the ability of state estimation to deal with bad data and improve the adaptability to non-smooth characteristics. The convergence of state estimation is improved as well as ensuring calculation accuracy.

AC/DC hybrid; converter; on-load-tap-changer; non-smooth characteristics

10.19783/j.cnki.pspc.220368

国家自然科学基金项目资助(52177125，51707196)

This work is supported by the National Natural Science Foundation of China (No. 52177125 and No. 51707196).

2022-03-20；

2022-04-08

巨云涛(1985—)，男，通信作者，博士，副教授，博士生导师，研究方向为高比例可再生能源系统的分布自律-集中协同的稳定分析与优化调控技术、分布式协同能量管理系统；E-mail: juyuntao@cau.edu.cn

黄 炎(1998—)，男，硕士研究生，研究方向为高比例可再生能源系统的分布自律-集中协同的稳定分析与优化调控技术。E-mail: yanhuang@cau.edu.cn

(编辑 许 威)