基于李雅普诺夫函数的带锁相环的VSC大扰动稳定性判据

李宇骏，华凤林，陆艺源，张 谦，杜正春

基于李雅普诺夫函数的带锁相环的VSC大扰动稳定性判据

李宇骏1，华凤林1，陆艺源1，张 谦2，杜正春1

(1.西安交通大学电力工程系，陕西 西安 710049；2.国网山西省电力公司电力科学研究院，山西 太原 030001)

对于带锁相环的并网VSC大扰动稳定性问题，首先依据VSC的内环电流控制和外环功率控制响应速度差异得到简化二阶非线性模型，然后分别定义了两个李雅普诺夫函数。第一个李雅普诺夫函数具有清晰的动能和势能概念，但推导的稳定域较小，第二个李雅普诺夫函数推导的稳定域较大但缺乏清晰的物理概念。最后结合这两个李雅普诺夫函数，得到实用的稳定性判据，兼具明确的物理意义和较宽的稳定域。如果在系统最后一次动作时已知锁相环状态量，则可以预测系统稳定性。仿真结果验证了该判据的正确性。

并网VSC；锁相环；大扰动稳定性；Lyapunov函数

0 引言

以太阳能和风能为代表的可再生能源在电力系统中的占比不断增大。可再生能源通常是换流器接入的发电设备(converter interfaced generation, CIG)，与同步发电机不同，CIG运行状态与其控制模式密切相关，这可能导致系统在遭受干扰时的运动轨迹与传统的运动轨迹有很大的不同[1]。VSC的控制主要包括内环电流控制、外环功率控制和锁相环(phase-locked loop, PLL)控制三部分，已有研究发现，在小扰动或因故障等原因引起的大扰动下，PLL可能会导致系统振荡，严重威胁高比例可再生能源电力系统的稳定性[2-3]。文献[4]发现当PLL无法跟踪电网相位时，风电场可能在严重短路故障下跳闸。因此，研究PLL影响下的VSC并网系统稳定性具有重要的意义。

研究含CIG的电力系统大扰动同步稳定性是十分困难的，因为其动力学行为由高阶非线性微分-代数方程描述，然而高阶系统的分析方法一般通过数值仿真获得时域解，以此分析VSC的运动趋势是失去同步还是保持稳定。但数值仿真的方法具有无法解析的固有缺点。文献[5]提出研究机电暂态时可以忽略新能源发电功率调节的快动态，认为功率能够快速达到控制策略的目标稳态。文献[6]提出了一种受PLL影响的VSC大干扰稳定性分析简化模型，其主要思想是忽略了VSC的快速内部电流控制和网络动态方程，只保留PLL控制方程。

现有文献中CIG的大扰动同步稳定分析方法主要有等面积判据(equal area criterion, EAC)法、相平面法和李雅普诺夫函数分析法等。EAC是以同步发电机组为主的传统电力系统进行大干扰稳定性分析的有效方法，文献[7]基于PLL方程和同步发电机组转子运动方程的相似性，利用EAC对系统的同步稳定性进行分析。文献[8]结合EAC和仿真计算进一步研究了快速电流控制对大扰动稳定性的影响。文献[9]计及虚拟惯量控制与低电压穿越，使用EAC分析了光伏暂态稳定性的影响因素。文献[10]采用EAC的思想，对基于PLL的多风电机组的暂态稳定性进行了分析。但由于PI控制器的比例环节会引入一个不定阻尼项，采用EAC进行分析时忽略了该项，可能导致估计的稳定域过于乐观[11]。

此外相平面图也是进行大扰动稳定性分析的有效工具，它包含了某一系统运行轨迹的速度变化和角度等信息，且可以刻画系统的稳定性边界。文献[12]采用相平面法对基于模块化多电平变流器的风电场在交流故障期间的大扰动稳定性进行了分析。文献[13]提出了一种利用Dommel-Sato迭代求解电力系统暂态网络电压封闭解的解析方法。然而，相平面法依赖大量的数值仿真以获得系统的轨迹。

李雅普诺夫方法被认为是分析非线性系统稳定性最有效的方法之一[14]。通过构造李雅普诺夫正定函数，无需依赖数值积分即可导出系统解析的保守稳定域。对于经典的两同步发电机系统，文献[15]证明了EAC和李雅普诺夫方法的一致性，其稳定边界由系统不稳定平衡点(unstable equilibrium point, UEP)的稳定流形确定。文献[16-17]基于同步发电机和VSC动力学特征的相似性，建立了适用于构网型换流器并网系统同步稳定性分析的李雅普诺夫函数。然而对于跟网型换流器并网系统而言，由于非线性阻尼项的存在，寻找正定李雅普诺夫函数较为困难。文献[18]基于李雅普诺夫理论导出了跟网型换流器并网系统的较小保守稳定域，文献[19]通过构造合适的李雅普诺夫函数导出更大的系统保守稳定域。为满足李雅普诺夫定理的约束，文献[20]将系统稳定域的估计转化为半正定优化问题，进而获得更大的系统保守稳定域。应用李雅普诺夫理论分析带PLL的并网VSC系统的稳定性研究虽然较多，但它们所导出的系统稳定域往往较小，保守性较大，难以应用于工程实际。因此，如何构造合适的李雅普诺夫函数，进而导出保守性较小的更大系统稳定域是一个挑战。

本文通过建模分析和时域仿真方法，根据VSC的内环电流控制响应速度远高于外环功率控制响应速度的特点，得到了研究大干扰稳定性的简化二阶非线性模型，考虑了不定阻尼项的影响，构造解析的李雅普诺夫函数计算得到保守的系统稳定域，且该域接近系统的真实稳定域。该稳定性判据反映了系统稳定域与PLL控制参数、VSC与无穷大系统的电气距离、系统工作点之间的解析关系。最后通过软件仿真验证了结果的准确性。

1 VSC并网模型

1.1 主电路模型

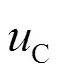
图1 VSC经传输线连接到无穷大母线的电路图

根据图1列写出静止abc三相坐标系下主电路的动态方程。

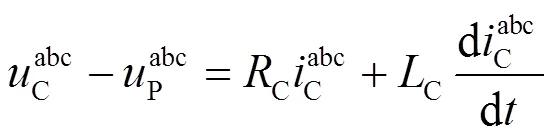
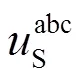
图2 矢量空间中不同坐标系间的关系

将静止abc坐标系下主电路的动态方程变换到坐标系下的动态方程。

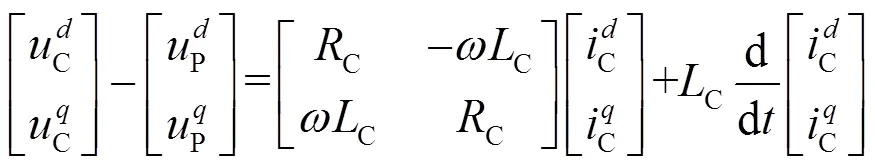
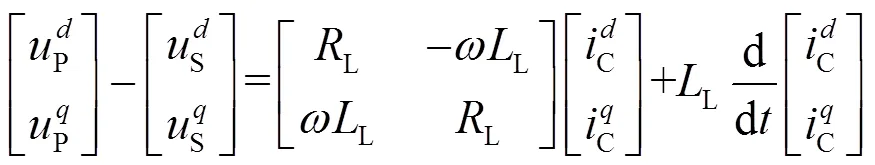
联立式(3)、式(4)可得式(5)。

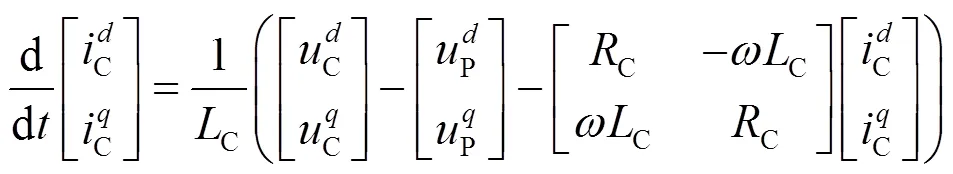
坐标系下S点处的电压如式(6)所示。

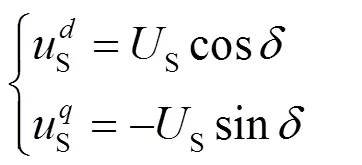
将式(6)代入式(4)得到式(7)。

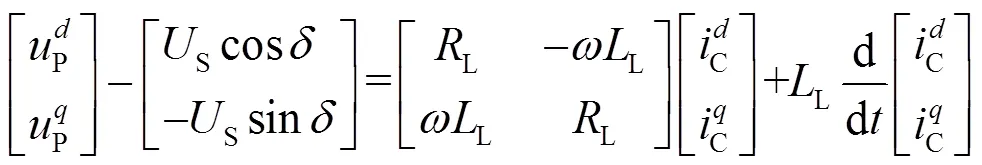
在坐标系下，VSC的有功功率和无功功率为

1.2 锁相环动态方程

PLL跟踪PCC点的相位，使得稳态时PCC点电压的轴分量为0，锁相环模型如图3所示。

根据图3写出PLL的动态方程[21]。

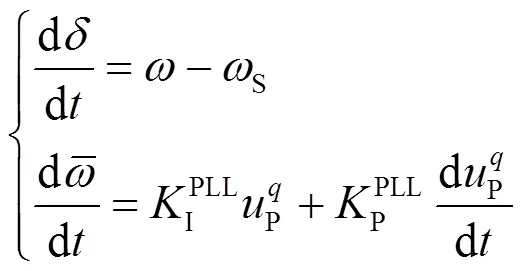
式中：；与有关。

1.3 内环电流控制动态方程

并网VSC的典型内环电流控制模型如图4所示，其控制需要变换到坐标下进行，变换角度由PLL提供。

图4 并网型VSC的内环电流控制模型

内环电流控制的动态方程如式(10)、式(11)所示[22]。

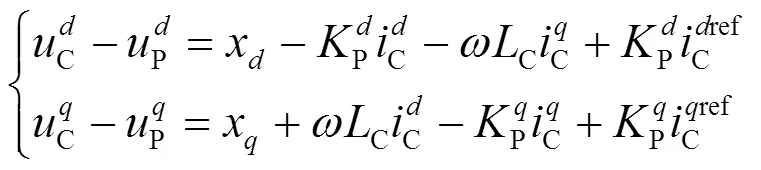
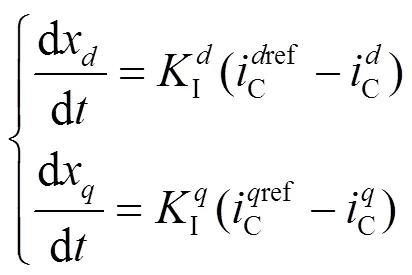
1.4 系统整体模型

将式(10)代入式(5)得到式(12)。

将式(12)代入式(7)得到式(13)。

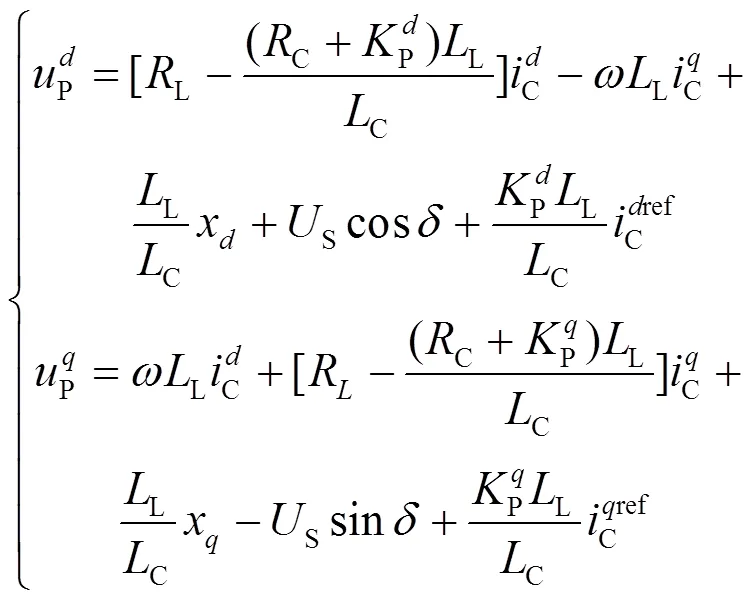
综上所述，微分方程式(9)、式(11)、式(12)和代数方程式(13)构成了本文研究系统的数学模型。

2 稳定性分析模型

2.1 系统的平衡点

稳态时系统运行在平衡点，此时系统模型中的微分方程式(9)、式(11)和式(12)两边的值均为0。用下标(0)表示稳态值。

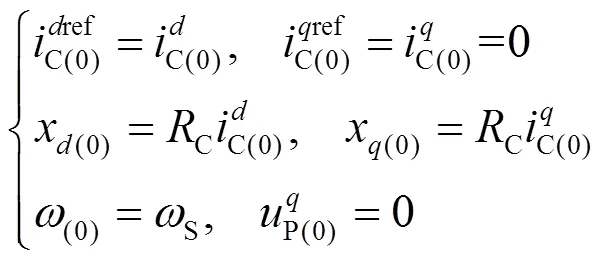
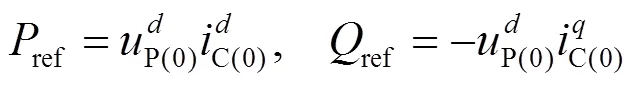
2.2 稳定性分析模型的简化

由于外环控制的响应速度远低于PLL控制的响应速度[23-24]，当分析PLL对并网VSC大扰动稳定性的影响时，外环控制参数可视为恒定的。

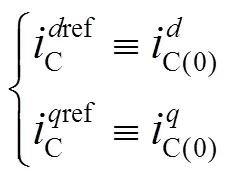
另一方面，电流内环的动态过程要远快于PLL的动态过程，因此可假设VSC输出的电流已达到参考值且稳定不变。

基于以上简化得到式(20)。

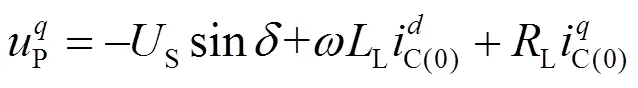
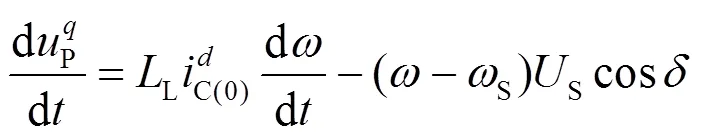
将式(21)代入式(9)，可得大扰动稳定性分析的简化模型。

式(23)描述的模型在文献[7]中已有出现，该模型与同步电机旋转方程有着相似的结构，因此可以采用EAC法、相平面法以及李雅普诺夫直接法分析其大扰动稳定性。

3 大扰动稳定性分析

3.1 李雅普诺夫函数I

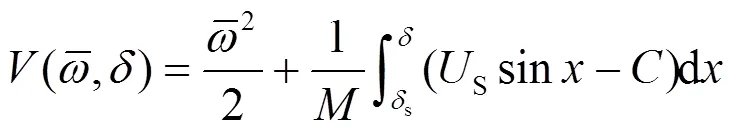
使其保持正定的定义域，如式(25)所示。

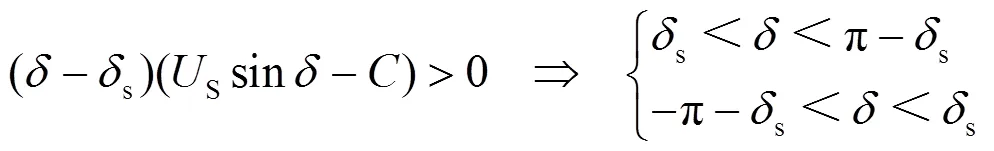
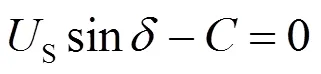
对式(24)的时间进行求导：

将式(22)代入式(27)得到

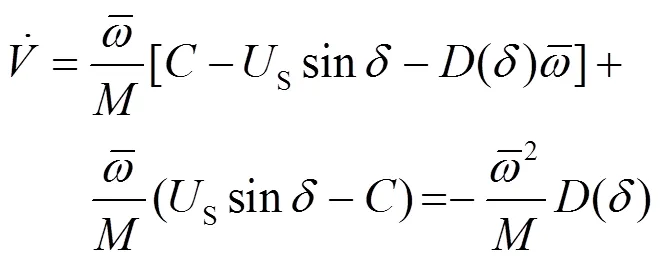
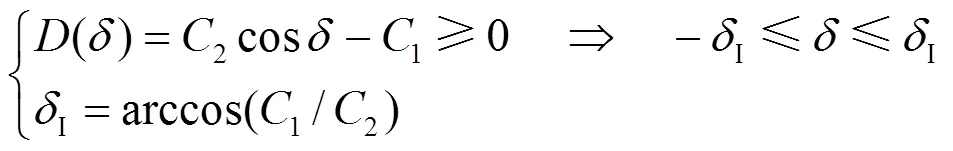
这种形式的李雅普诺夫函数具有明确的物理意义，式(24)中第一项类似于系统的动能，第二项类似于系统的势能。

3.2 李雅普诺夫函数II

不同的李雅普诺夫函数得到的系统稳定域不同，为了尽可能地接近真实的稳定域，本文提出一个新的李雅普诺夫函数。改写式(22)得到式(30)。

则式(22)可改写为

构造李雅普诺夫函数：

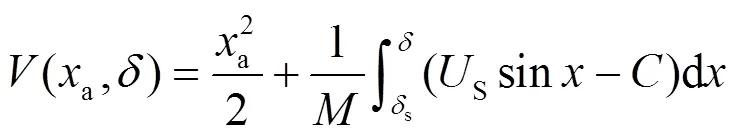
使其保持正定的定义域，如式(25)所示。

对式(33)的时间进行求导：

将式(32)代入式(34)可得

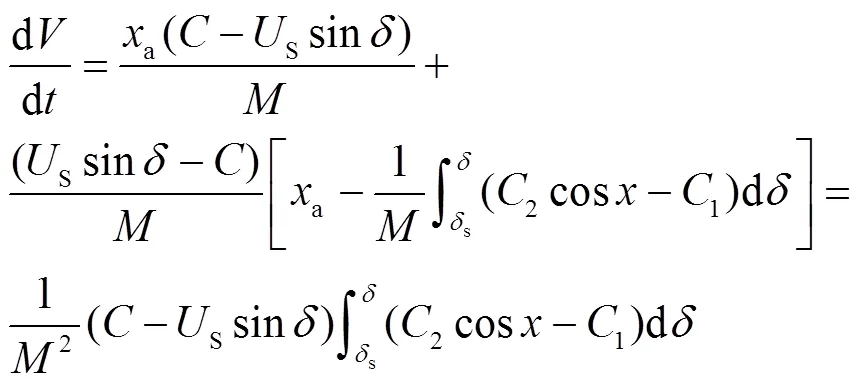
类似地，根据李雅普诺夫定理，得到系统在平衡点处稳定的条件。

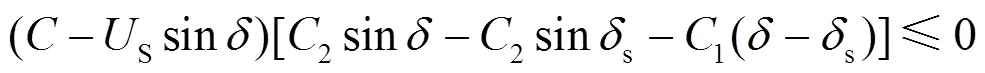
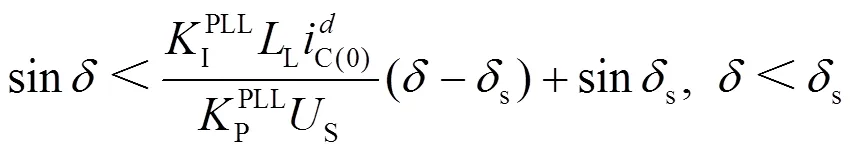
结合式(37)、式(38)，由该李雅普诺夫函数推导得到的系统稳定域如式(39)所示。

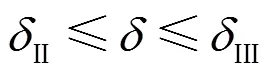
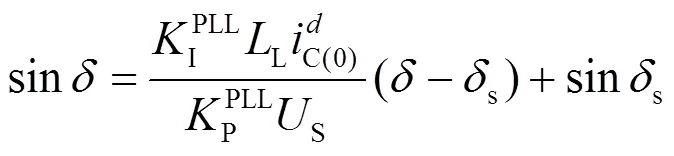
图5比较了系统参数变化下两种李雅普诺夫函数导出的稳定域大小。图5(a)比较了不同PLL参数对系统稳定域的影响，增大PLL的比例系数，可以增加系统稳定域，同时，减小PLL的积分系数，亦可增大系统稳定域。图5(b)比较了不同有功参考值和线路电感对系统稳定域的影响，从图中可知，减小有功参考值或线路电感，均可以增加系统稳定域。

此外，从图5中可清晰地看出，由第二个李雅普诺夫函数导出的稳定域比第一个李雅普诺夫函数导出的稳定域大，故李雅普诺夫函数II导出的稳定域保守性更弱。

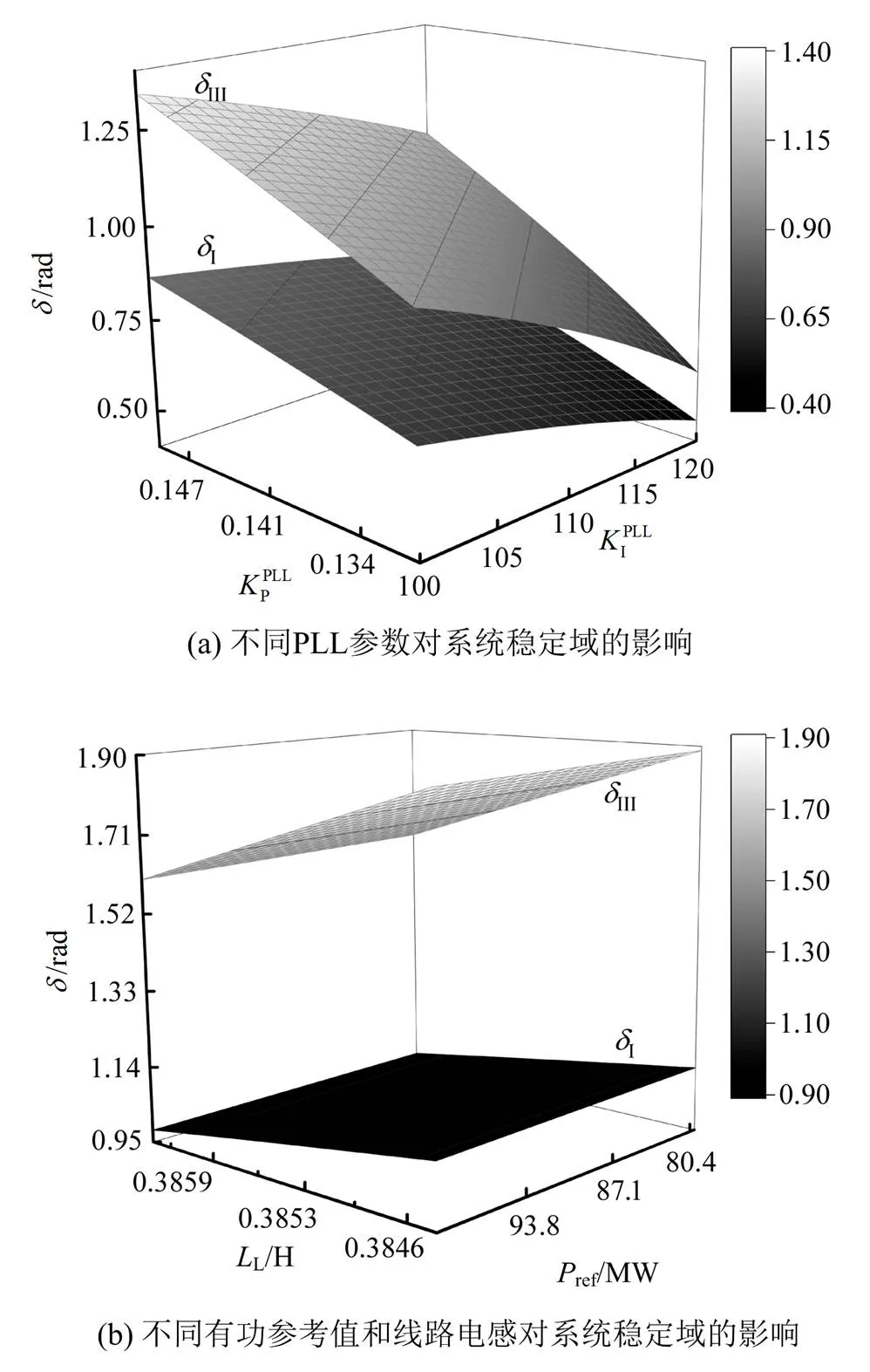
图5 不同参数下两种李雅普诺夫函数导出的系统稳定域

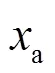
综上所述，首先利用李雅普诺夫函数II导出保守性较小的稳定域，然后用信号获取方便、物理意义明确的李雅普诺夫函数I进行稳定性判断。

4 仿真计算

在PSCAD仿真软件中对上文所述的大扰动情况进行仿真计算。仿真模型采用图1所示的VSC经传输线接入无穷大母线的模型，传输线采用经典RL模型。系统参数的选取如表1所示。

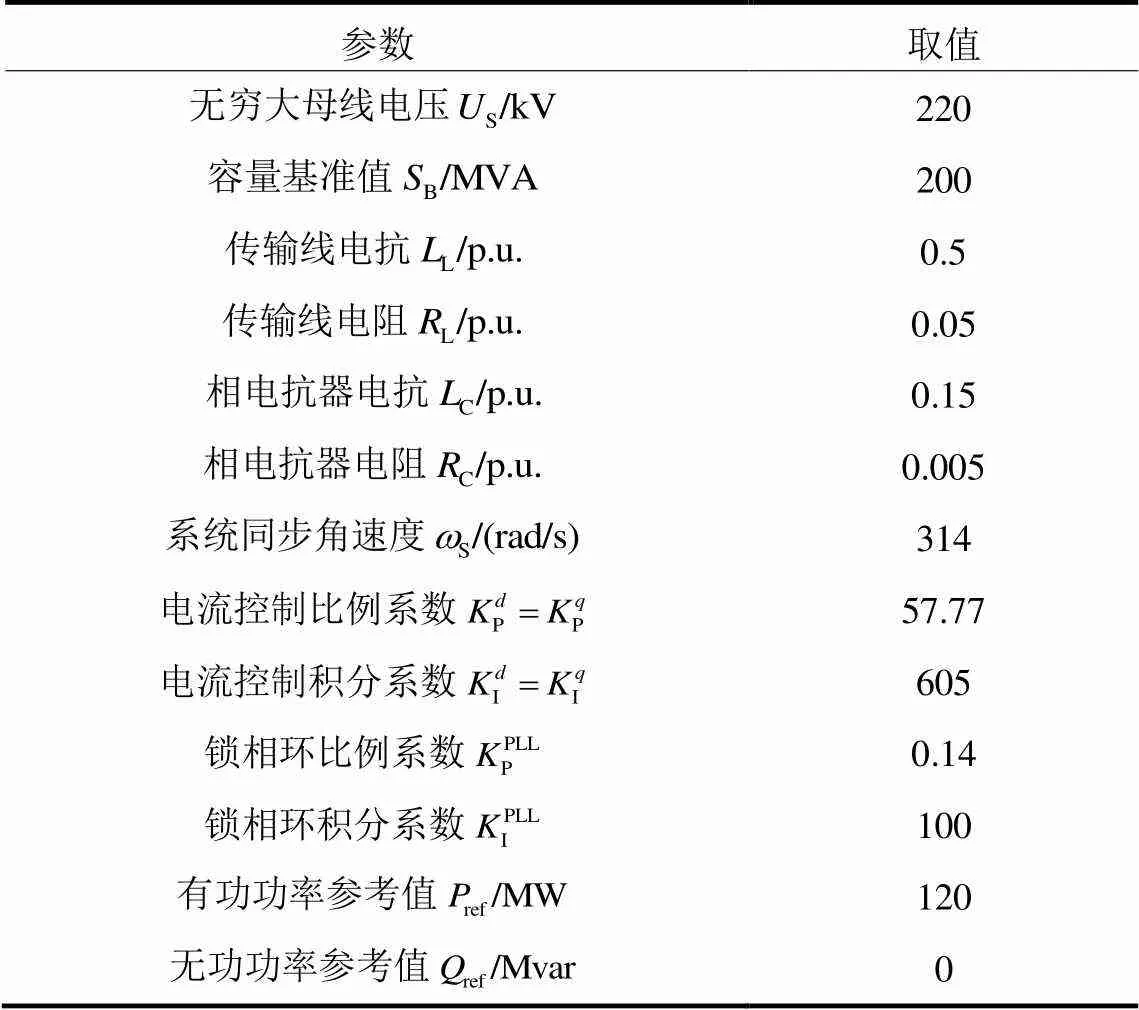
表1 并网VSC系统的参数选取

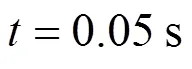
图7比较了简化模型和全阶模型在不同的故障切除时间下故障期间的动态过程，实线为本文提出模型的动态过程，虚线为详细模型的动态过程。由图7(a)、图7(b)可知，当故障被及时切除，两种模型下系统均能保持稳定，随着故障切除时间的延长，振荡幅度不断增大，振荡的衰减速度不断减小，逐渐增大故障切除时间至系统失稳，失稳系统的动态过程如图7(c)、图7(d)所示。二者的阻尼振荡相似，由此验证了该模型在大干扰稳定性分析问题中的准确性。

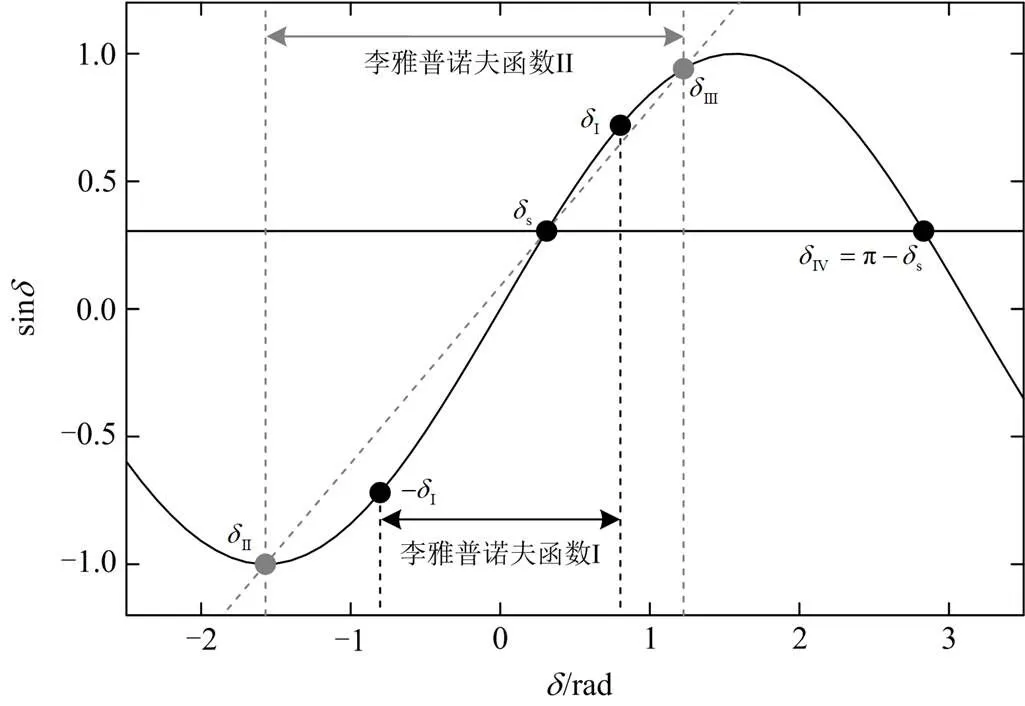
图6 仿真算例下两种李雅普诺夫函数导出的系统稳定域

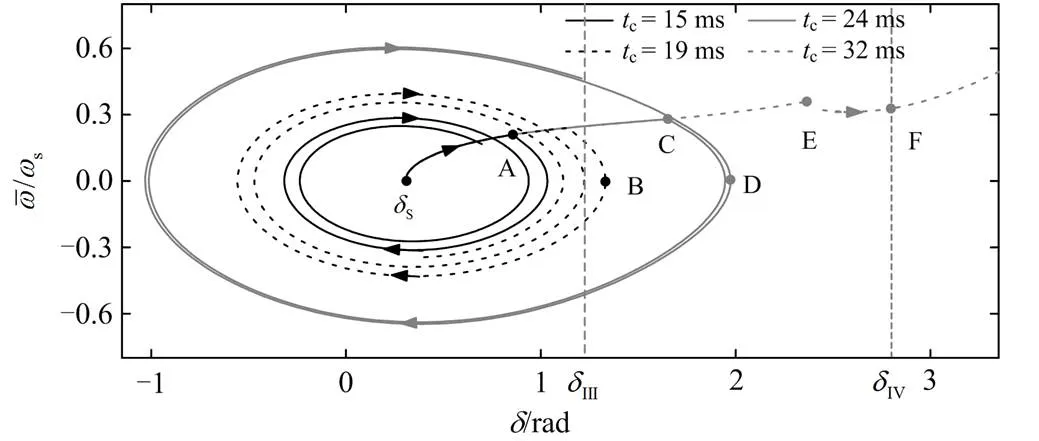
图8 电压突降情况下的相平面图

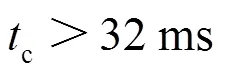
表2 系统的极限值

表3 李雅普诺夫函数的极限值

5 结论

本文通过李雅普诺夫直接法分析单VSC接口电源通过传输线连接到无穷大母线系统的大扰动同步稳定性。在合理考虑VSC内部电流控制和外部功率控制的时间尺度差异的基础上，对并网VSC的全阶模型进行了降阶，得到一种包含阻尼项的简化二阶非线性模型。考虑阻尼项，提出了一种新的李雅普诺夫函数，与以往的李雅普诺夫函数相比，得到了保守程度更低的稳定域。在系统最后一次动作时已知锁相环状态量的情况下，可以保守预测系统的稳定性。

[1] ERDIWANSYAH, MAHIDIN, HUSIN H, et al. A critical review of the integration of renewable energy sources with various technologies[J]. Protection and Control of Modern Power Systems, 2021, 6(1): 37-54.

[2] 张琛, 蔡旭, 李征. 电压源型并网变流器的机-网电气振荡机理及稳定判据研究[J]. 中国电机工程学报, 2017, 37(11): 3174-3183.

ZHANG Chen, CAI Xu, LI Zheng. Stability criterion and mechanisms analysis of electrical oscillations in the grid-tied VSC system[J]. Proceedings of the CSEE, 2017, 37(11): 3174-3183.

[3] 郑超航, 李华. 弱电网下电压源型变换器静态稳定性分析[J]. 电力系统保护与控制, 2021, 49(17): 38-47.

ZHENG Chaohang, LI Hua. Static stability analysis of voltage source converters connected to a weak grid[J]. Power System Protection and Control, 2021, 49(17): 38-47.

[4] HAO Yuan, YUAN Xiaoming, HU Jiabing. Modeling of grid-connected VSCs for power system small-signal stability analysis in DC-link voltage control timescale[J]. IEEE Transactions on Power Systems, 2017, 32(5): 3981-3991.

[5] 陈磊, 刘永奇, 戴远航, 等. 电力电子接口新能源并网的暂态电压稳定机理研究[J]. 电力系统保护与控制, 2016, 44(9): 15-21.

CHEN Lei, LIU Yongqi, DAI Yuanhang, et al. Study on the mechanism of transient voltage stability of new energy source with power electronic interface[J]. Power System Protection and Control, 2016, 44(9): 15-21.

[6] MA Shaokang, GENG Hua, LIU Lu, et al. Grid- synchronization stability improvement of large scale wind farm during severe grid fault[J]. IEEE Transactions on Power Systems, 2018, 33(1): 216-226.

[7] HU Qi, FU Lijun, MA Fan, et al. Large signal synchronizing instability of PLL-based VSC connected to weak AC grid[J]. IEEE Transactions on Power Systems, 2019, 34(4): 3220-3229.

[8] HU Qi, FU Lijun, MA Fan, et al. Analogized synchronous-generator model of PLL-based VSC and transient synchronizing stability of converter dominated power system[J]. IEEE Transactions on Sustainable Energy, 2021, 12(2): 1174-1185.

[9] 田雨果, 王彤, 邢其鹏, 等. 计及虚拟惯量控制与低电压穿越的光伏发电系统暂态稳定分析[J]. 电力系统保护与控制, 2022, 50(2): 52-59.

TIAN Yuguo, WANG Tong, XING Qipeng, et al. Transient stability analysis of a photovoltaic generation system considering virtual inertia control and low voltage ride-through[J]. Power System Protection and Control, 2022, 50(2): 52-59.

[10] 柳飞扬, 曾平, 李征. 电网故障下全功率风电场内部机组的暂态稳定性分析[J]. 电力系统保护与控制, 2022, 50(5): 43-54.

LIU Feiyang, ZENG Ping, LI Zheng. Transient stability analysis of wind turbines with a full-scale converter under grid fault[J]. Power System Protection and Control, 2022, 50(5): 43-54.

[11] ZHANG Chen, MOLINAS M, LI Zheng, et al. Synchronizing stability analysis and region of attraction estimation of grid-feeding VSCs using sum-of-squares programming[J]. Frontiers in Energy Research, 2020, 8: 1-12.

[12] TAUL M G, WANG Xiongfei, DAVARI P, et al. An overview of assessment methods for synchronization stability of grid-connected converters under severe symmetrical grid faults[J]. IEEE Transactions on Power Electronics, 2019, 34(10): 9655-9670.

[13] 康卓然, 张谦, 陈民权, 等. 适用于电力系统暂态稳定分析的网络电压解析算法研究[J]. 电力系统保护与控制, 2021, 49(3): 32-38.

KANG Zhuoran, ZHANG Qian, CHEN Minquan, et al. Research on network voltage analysis algorithm suitable for power system transient stability analysis[J]. Power System Protection and Control, 2021, 49(3): 32-38.

[14] 纪锋, 高路, 崔翔, 等. VSC瞬时电流控制及李雅普诺夫稳定性分析[J]. 中国电机工程学报, 2020, 40(13): 4142-4150.

JI Feng, GAO Lu, CUI Xiang, et al. Instantaneous current control of VSC and Lyapunov stability analysis[J]. Proceedings of the CSEE, 2020, 40(13): 4142-4150.

[15] GLESS G E. Direct method of Liapunov applied to transient power system stability[J]. IEEE Transactions on Power Apparatus and Systems, 1966, PAS-85(2): 159-168.

[16] 沈超, 帅智康, 程慧婕. 虚拟同步机并联电流控制型变换器系统暂态同步稳定性分析[J]. 电力系统自动化, 2021, 45(10): 115-123.

SHEN Chao, SHUAI Zhikang, CHENG Huijie. Transient synchronization stability analysis of system with paralleled virtual synchronous generators and current-controlled converters[J]. Automation of Electric Power Systems, 2021, 45(10): 115-123.

[17] LORENZETTI P, KUSTANOVICH Z, SHIVRATRI S, et al. The equilibrium points and stability of grid-connected synchronverters[J]. IEEE Transactions on Power Systems, 2022, 37(2): 1184-1197.

[18] MANSOUR M Z, ME S P, HADAVI S, et al. Nonlinear transient stability analysis of phase-locked loop based grid-following voltage source converters using Lyapunov’s direct method[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2022, 10(3): 2699-2709.

[19] ZHANG Yu, ZHANG Chen, CAI Xu. Large-signal grid-synchronization stability analysis of PLL-based VSCs using Lyapunov’s direct method[J]. IEEE Transactions on Power Systems, 2022, 37(1): 788-791.

[20] ZHANG Ziqian, SCHUERHUBER R, FICKERT L, et al. Domain of attraction’s estimation for grid connected converters with phase-locked loop[J]. IEEE Transactions on Power Systems, 2022, 37(2): 1351-1362.

[21] WEN Bo, BOROYEVICH D, BURGOS R, et al. Analysis of D-Q small-signal impedance of grid-tied inverters[J]. IEEE Transactions on Power Electronics, 2016, 31(1): 675-687.

[22] ZHOU J Z, DING Hui, FAN Shengtao, et al. Impact of short-circuit ratio and phase-locked-loop parameters on the small-signal behavior of a VSC-HVDC converter[J]. IEEE Transactions on Power Delivery, 2014, 29(5): 2287-2296.

[23] MORRIS J F, AHMED K H, EGEA-ALVAREZ A. Analysis of controller bandwidth interactions for vector- controlled VSC connected to very weak AC grids[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2021, 9(6): 7343-7354.

[24] WU Guanglu, SUN Huadong, ZHANG Xi, et al. Parameter design oriented analysis of the current control stability of the weak-grid-tied VSC[J]. IEEE Transactions on Power Delivery, 2020, 36(3): 1458-1470.

Large disturbance stability criterion for a VSC with phase-locked loop based on a Lyapunov function

LI Yujun1, HUA Fenglin1, LU Yiyuan1, ZHANG Qian2, DU Zhengchun1

(1. Department of Electrical Engineering, Xi’an Jiaotong University, Xi'an 710049, China; 2. Electric Power Research Institute of State Grid Shanxi Electric Power Company, Taiyuan 030001, China)

To study the large disturbance stability of a grid-connected VSC with phase-locked loop, a simplified second order nonlinear model of a VSC is established based on the difference of response speed between inner loop current control and outer loop power control, and two Lyapunov functions are separately defined. The first Lyapunov function has clear kinetic energy and potential energy concepts but a small stable region, while the second Lyapunov function has a wider stable region but lacks clear physical concepts. Combining the two Lyapunov functions, a practical stability criterion is obtained, one which has both clear physical concepts and a relatively large stable region.If the state of the phase-locked loop is known at the time of the system’s last operation, the stability can be predicted. The simulation results well verify the accuracy of the derived stability criterion.

grid-connected VSC; phase-locked loop; large disturbance stability; Lyapunov function

10.19783/j.cnki.pspc.220262

国家电网有限公司总部科技项目资助(5100- 202055389A-0-0-00)

This work is supported by the Science and Technology Project of the Headquarters of State Grid Corporation of China (No. 5100-202055389A-0-0-00).

2022-03-03；

2022-06-05

李宇骏(1990—)，男，通信作者，博士，副教授，研究方向为高比例新能源电力系统大扰动稳定性分析；E-mail: yujunli@xjtu.edu.cn

华凤林(1998—)，女，硕士，研究方向为电力系统稳定性分析；E-mail: huafenglinv@stu.xjtu.edu.cn

陆艺源(1996—)，男，博士，研究方向为电力系统稳定性分析。E-mail: luyiyuan961015@stu.xjtu.edu.cn

(编辑 许 威)