风电调频补偿水锤效应的频率特性分析

朱 博，束洪春，吴水军，黄柯昊，孙士云，邓 涵

风电调频补偿水锤效应的频率特性分析

朱 博1，束洪春1，吴水军2，黄柯昊1，孙士云1，邓 涵1

(1.昆明理工大学，云南 昆明 650051；2.云南电力试验研究院(集团)有限公司，云南 昆明 650217)

水轮机在云南电网中占比很大，为了解决水轮机的水锤效应带来的功率反调现象，提出了一种考虑风电调频特性补偿水锤效应的分析方法。首先，建立了含风、水、网、荷的简单系统数学模型。其次，使用直流潮流法得到水轮机及其调频策略、风机及其调频策略所对应的代数微分方程和系统网络方程。并在此基础上进行线性化处理，推导出负荷扰动时水轮机和风机并网节点频率响应的频域解析式。根据解析式分析调频控制参数等对系统频率的影响。最后，通过以双机系统及实际电网的仿真分析对风机补偿水轮机水锤效应的有效性和可行性进行了验证。

异步联网；风电调频；水锤效应；调频指标

0 引言

随着能源枯竭和环境污染的日益严重，以风电为代表的可再生能源在电力系统中的接入比例越来越高，风电相比于光伏发电、潮汐发电、垃圾焚烧发电等来说，技术优势突出、发展潜力大，因此风电受到的关注度持续升高，但由于风电功率波动性强、随机性强，传统调频资源的响应速度及爬坡速度难以应对，高渗透率风电波动会对系统频率产生不利影响，使得电力系统一次调频负担加重。故风电场参与一次调频对风电并网后的运行有重要意义[1-3]。为了减少新能源装机容量逐年增长对系统调频的危害，以及防止高周切机现象，需要新能源积极参与调频过程，以解决异步联网后网内故障点发生时刻开始0~6 s内调频容量不足的实际问题。

异步联网后作为送端系统的云南电网，其频率问题主要体现在当电力系统突然失去负荷或向非同步系统送电的直流输电通道突然发生闭锁时，系统的频率升高。此时传统同步发电机的一次调频功能将发挥作用，抑制系统频率的上升。若传统发电机的一次调频能力不足，系统频率的升高可能触发电网第三道防线动作，引起高周切机。水电机组存在的水锤效应[4-5]将导致水轮机参与调频的初期引起功率反调现象，造成电网频率升高问题。如何有效地挖掘高渗透率风电机组的一次调频能力，以补偿水锤效应带来的功率反调现象是亟需解决的实际问题。

目前双馈风机已成为风电产业中应用最为广泛的主流机型。然而，双馈风机具有风能波动性、随机性和间歇性的特点，使电力系统的稳定性受到不可忽视的影响。文献[6]根据双馈风机的原理进行分析，以虚拟惯性控制提供短暂的频率支撑，下垂控制改善系统的稳态频率偏差。限功率运行下进行减载控制，留有部分功率备用，高风速下以桨距角控制风机出力，并整定了系统的调差系数，改善了系统的下垂控制特性，最后制定了适应变风速下的变系数控制方法。文献[7]提出基于惯量控制和下垂控制的变速型风机频率协调控制策略，并分析了在不同扰动条件下，不同惯性参数与下垂参数对孤立电力系统频率的影响。文献[8]针对双馈变速风电机组采用双脉宽调制变流器实现电磁转矩与机械转矩的解耦控制，可以实现对频率的响应控制，但该方法响应速度较慢。文献[9]从风电并网所带来的电能质量、经济性、负荷支撑、快速响应性等考虑，提出了高风电渗透率下风电机组参与系统频率调整的多时间尺度协调优化策略，该项策略表明双馈风机能有效地为系统提供惯性支撑且具备灵活、可控的静态频率响应特性。文献[10]针对异步联网运行后西南电网控制需求，构建了西南电网频率稳定防控体系，提出了直流频率控制器与一次调频、AGC 的协调配合策略以及多直流协调紧急功率调制措施。文献[11]提出了双馈风机的变速线性化模型，更好地结合现有的系统频率响应模型来研究电力系统频率的变化。文献[12-13]研究电网限负荷条件下风电机组参与系统一次频率调整，根据不同风况通过超速减载控制与桨距角相配合的控制方法，即改善双馈风电机组的调频特性也能有效减少弃风。

目前针对风电和水电在调频方面互补配合的主要都是对风电水电联合运行研究机组组合经济性，文献[14]针对各发电机组的调频特性采用了不同的控制策略，使系统面对频率波动时调频范围更广、适用性更强。文献[15]为了最大化电力系统经济效益，计及抽水蓄能电站的启停费用和偏离计划出力的惩罚费用，建立了系统的优化调度模型。模型还考虑了抽水蓄能电站蓄水量、发电机组启停等约束条件从而使系统更能切合实际情况。文献[16]考虑了由风力发电机组和柴油发电机组组成的电网，提出了一种新的减少频率和功率偏差的排列方式。文献[17]基于风电水电能源的特性，构建了风电-水电联合发电模型，结果表明联合发电模型可以减弱风电波动性和水电的季节性对电力系统的影响。文献[18]对3个系统(加拿大魁北克系统、美国太平洋西北部地区 BPA 系统以及北欧 NNP 系统)的风电场和水电厂联合发电的运行状况进行分析与评估，结果显示风电-水电联合系统改善了电力系统的技术优势和经济优势。文献[19-20]针对云南地区的风能、水能以及气候、地理位置，提出利用风能、水能的互补性能较好地改善电力特性，提高送出线路的利用率，同时使得风电的消纳问题也得到了解决。文献[21]针对风电和水电的出力和调频特性以及水轮机的水锤效应，综合分析调频控制方法和系统旋转备用对系统频率动态和稳态特性的影响，提出一种感应水轮机导水叶变化并结合风电虚拟惯性控制、下垂控制的新的一次调频控制方法。

为了衡量新能源参与一次调频起到的作用，需要恰当的评价指标。文献[22-23]借鉴水火电参与电网调频的考核指标，对风电场参与电网调频的功率指标参数做了归纳，并用指标对仿真结果做了评价，指标主要有一次调频死区、响应滞后时间、响应时间、调节时间和调频控制偏差等。文献[24-25]对风电场参与电网调频的频率指标参数做了详细研究，把一次调频分为了频率下降阶段，频率恢复阶段和频率稳定阶段。同时提出了5个衡量系统频率响应的指标：最低点频率、稳态频率、最低点频率响应、稳态频率响应、频率初始下降率。

国内外学者在风电弥补水锤效应方面开展了大量的研究工作，其中一部分文献结合了异步联网系统送端电网的特有现状，采用风机参与一次调频来补偿水轮机组水锤效应，在一定程度上抑制了因为水锤效应引起的功率反调而导致的电网频率波动，这些文献主要从仿真分析的角度做了大量工作，而风电调频补偿水锤效应的频率特性解析推导以及较为全面的影响因素分析仍有待深入，本文将主要针对该部分内容展开研究工作。

1 双馈风机并网点频率特性解析推导

首先建立含风、水两种电源和负荷的系统数学模型，借鉴文献[26]中提出的方法，使用直流潮流法形成一个含风机、水轮机和负荷电磁功率的网络潮流增量方程，在此基础上考虑水轮机典型的调速器传递函数和风机采用下垂调频控制策略，在频域下分别解析得到负荷变化时风机和水轮机并网节点频率响应的表达式。

1.1 水轮机数学模型

忽略励磁及调节系统的影响，同步水轮发电机的经典二阶模型为

水轮机调速器和原动机部分采用的模型如图1所示。

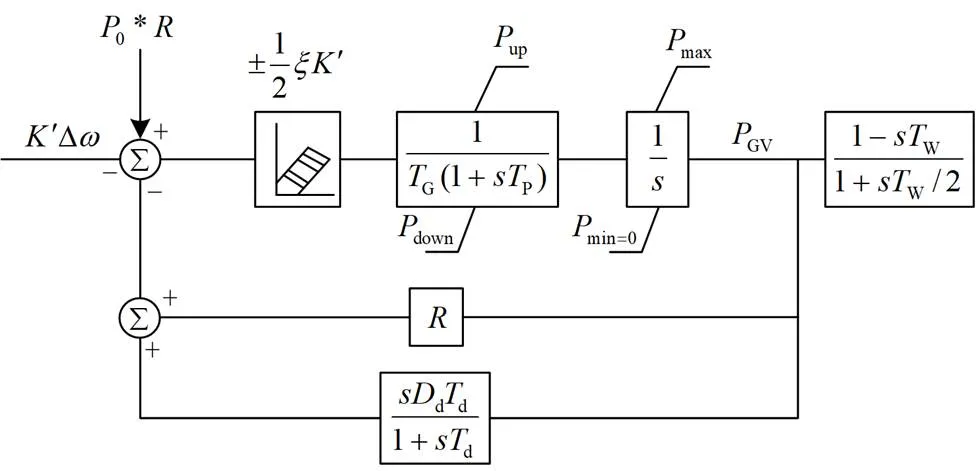
图1 水轮机调速器和原动机模型

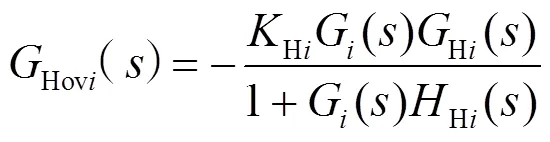
原动机调速器部分的机械功率增量方程可表示为

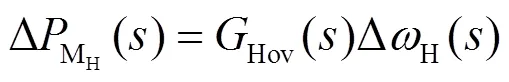
1.2 风机数学模型

风机由于双馈风机中齿轮箱的存在，其传动系统的模型可以采用原动机和发电机分别单独考虑的双质量块详细模型，也可以采用原动机和发电机作为一个整体的单质量块简化模型，本文采用单质量块简化模型。

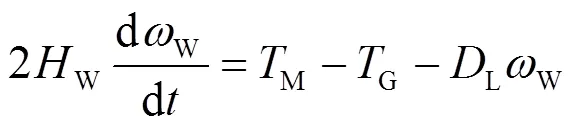
下垂控制具有构建系统便捷、可以改善双馈风机响应系统频率变化特征等优点，故本文中风电机组选用下垂控制策略参与系统一次调频，控制模型框图如图2所示。

图2 系统频率控制模型

风机采用下垂控制，忽略该调速器中幅值限幅等非线性环节，根据图2可以得到复频域下的简化传递函数为

原动机调速器部分的增量方程可表示为

1.3 电网简化数学模型

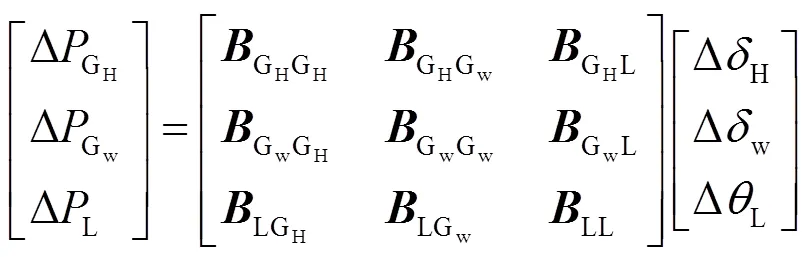
为方便计算，将忽略阻尼系数的式(1)和式(4)转化为频域下的公式，如式(8)所示。

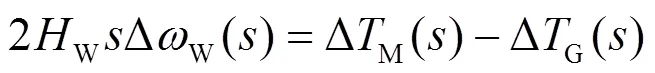
为了方便引入水轮机和风机调频控制方程，在复频域下将式(7)展开后得到

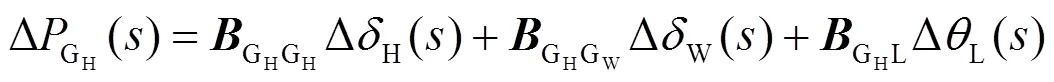
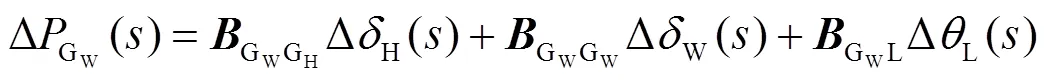
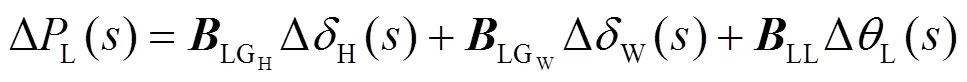
由式(10)和式(12)消去Δ后得到水轮机电磁功率增量与负荷扰动之间的关系，如式(13)所示。

由式(11)和式(12)消去Δ后得到风机电磁功率增量与负荷扰动之间的关系，如式(14)所示。

将式(3)代入式(8)化简后得到水轮机电磁功率增量与水轮机转子角速度增量之间的关系，如式(15)所示。

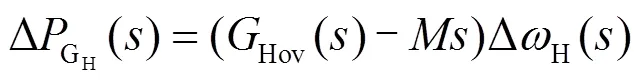
综合式(6)、式(13)、式(14)和式(15)可分别得到发生负荷扰动情况下风机和水轮机并网节点频率的频域响应为

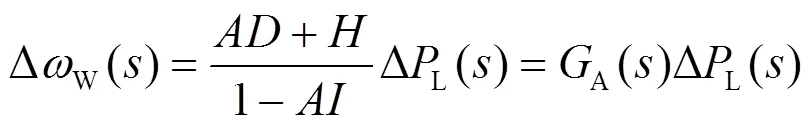
式中具体变量的表达式见附录A。

2 双馈风机弥补水锤效应影响因素分析

建立含风机、水轮机和负荷的双机系统，如图3所示，分析双馈风机并网节点频率的影响因素和变化规律。发电机1为水轮机，发电机2为风机，负荷接在母线A上。

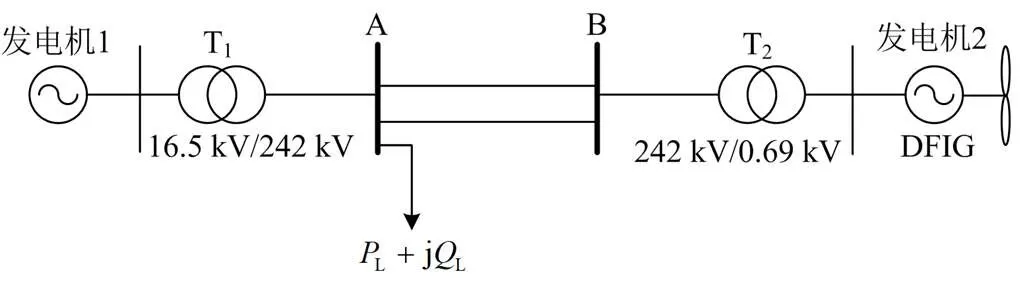
图3 双机系统接线图

在图3所示系统中，发电机1基准电压为16.5 kV，双馈风力发电机2基准电压为0.69 kV，母线A处有功负荷为100 MW，无功负荷为60 MW，变压器T1变比为16.5 kV/242 kV，变压器T2变比为0.69 kV/242 kV，变压器T1处阻抗为j0.0567 Ω，变压器T2处阻抗为j0.0625 Ω，母线A和母线B由双回输电线路连接，阻抗均为0.01+j0.0850 Ω，调频控制仿真参数等如表1所示。

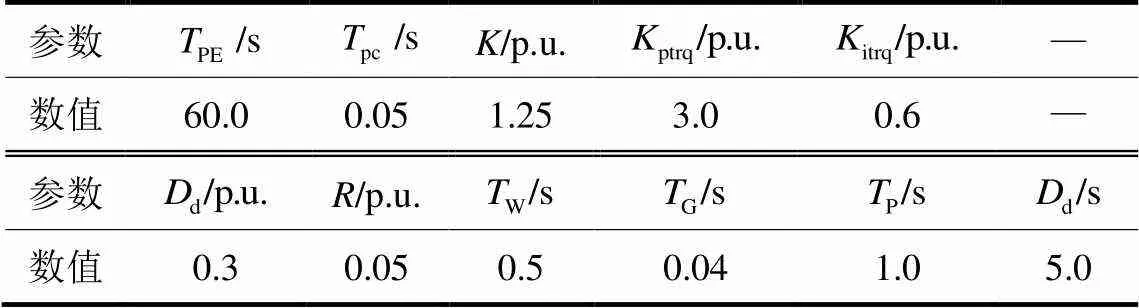
表 1 双机系统仿真参数

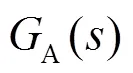
图4 系统频率响应极点分布图

2.1 水锤效应时间常数的影响

由表2可知，当水锤效应时间常数从0.5 s变化到2.0 s时，系统主导共轭极点更加靠近虚轴，阻尼比减小，系统响应变慢，系统的振荡趋势增大，抗高频扰动性能下降。由此可见，水锤效应时间常数越高，对系统的频率影响越大，系统调频性能越差。在图3所示系统中，考虑不同水锤效应时间常数下，分析双馈风机采用下垂控制策略参与一次调频时的频率差异，风机频率偏差曲线如图5所示。

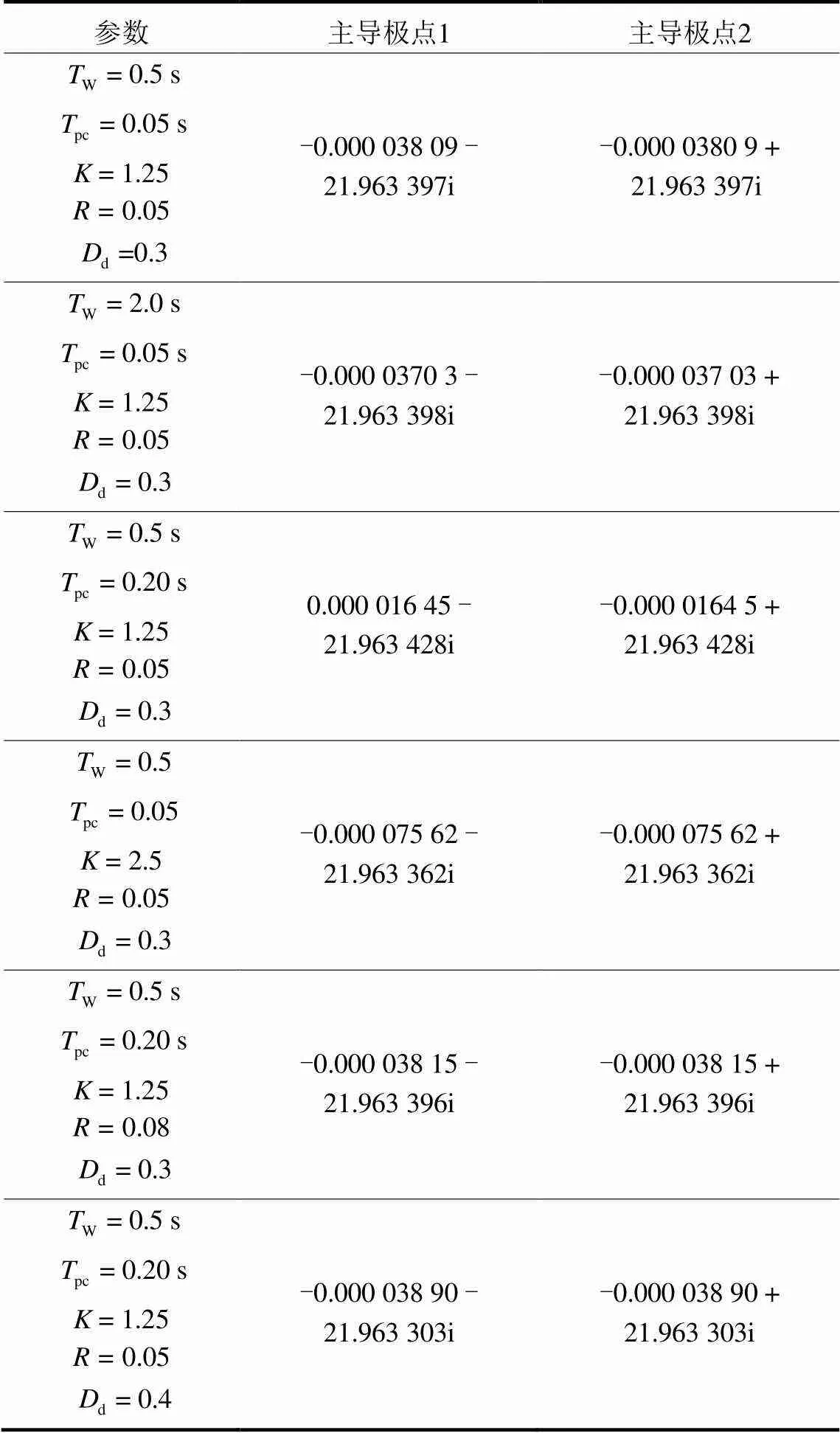
表 2 不同参数对调频性能的影响

图5 不同水锤效应时间常数下的风机频率偏差曲线

由式(16)可以画出在阶跃负荷扰动下，双馈风机并网节点频率和水锤效应时间常数二者之间在频域下的变化趋势，如附录A中图A1所示。由图A1可见，随着水锤系数的增大，角频率的偏差值也随之增大，系统调频性能变差。

2.2 水轮机调频控制参数的影响

调差系数的物理意义为机组功率改变1%时频率偏移的百分比，其值决定了发电机稳态转速与负荷的关系。由表2可知，当调差系数从0.05变化到0.08时，系统主导共轭极点则更加远离虚轴，阻尼比增大，系统响应变快，系统的振荡趋势减小，系统调频性能变好。当软反馈环节系数从0.3变化到0.4时，系统主导共轭极点则更加远离虚轴，阻尼比增大，系统响应变快，系统的振荡趋势减小，系统调频性能变好。在图3所示系统中，考虑不同水轮机调频控制参数下，分析双馈风机采用下垂控制策略参与一次调频时的频率差异，风机频率偏差曲线如图6和图7所示。

图6 不同调差系数下风机频率偏差曲线

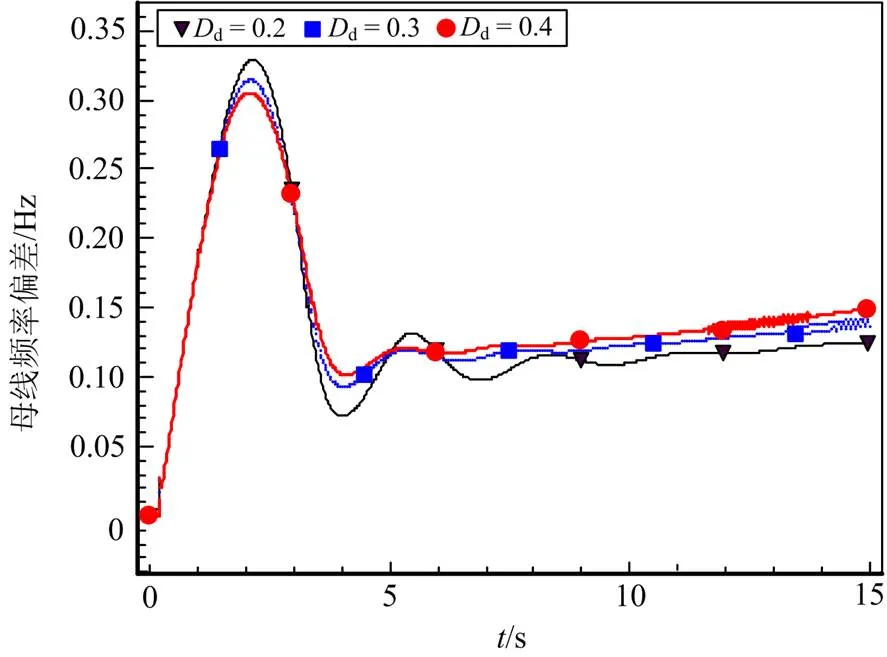
图7 不同软反馈环节系数下风机频率偏差曲线

由式(16)画出图3所示系统在负荷阶跃扰动下，风机并网节点的频率响应随水轮机调频控制参数的变化趋势，如附录A中图A2和图A3所示。由图A2和图A3可见，随着调差系数的增大，系统的最大频率偏差量略微减小，而随着软反馈环节系数的最大频率偏差量明显减小，系统调频性能均变好。

2.3 风机调频控制参数的影响

由表2可知，当惯性环节时间常数从0.05 s变化到0.20 s时，系统主导共轭极点更加靠近虚轴，阻尼比减小，系统响应变慢，系统的振荡趋势增大，抗高频扰动性能下降。当下垂控制系数从1.25变化到2.5时，系统主导共轭极点则更加远离虚轴，阻尼比增大，系统响应变快，系统的振荡趋势减小，系统调频性能变好。在图3所示系统中，考虑不同调频控制参数下，分析双馈风机采用下垂控制策略参与一次调频时的频率差异，风机频率偏差曲线如图8和图9所示。

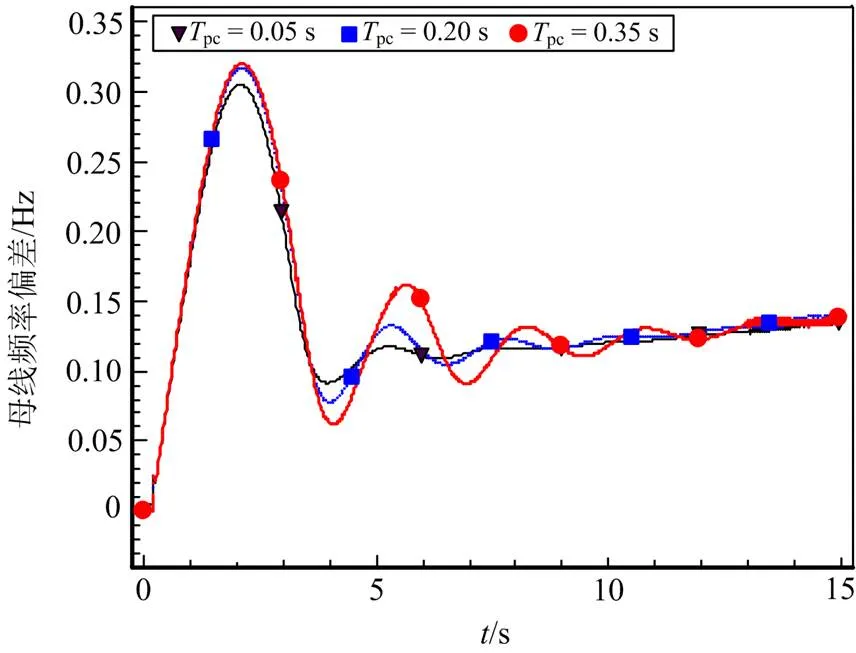
图8 不同时间常数下的风机频率偏差曲线

图9 不同下垂控制系数下的风机频率偏差曲线

由式(16)画出图3所示系统在负荷阶跃扰动下，风机并网节点的频率响应随调频控制参数的变化趋势，如附录A中图A4和图A5所示。由图A4和图A5可见，随着惯性环节时间常数的增大，频率偏差量也随之增大，系统调频性能变差，而随着下垂控制系数的增大，频率偏差量随之减小，系统调频性能变好。

2.4 风电响应时延的影响

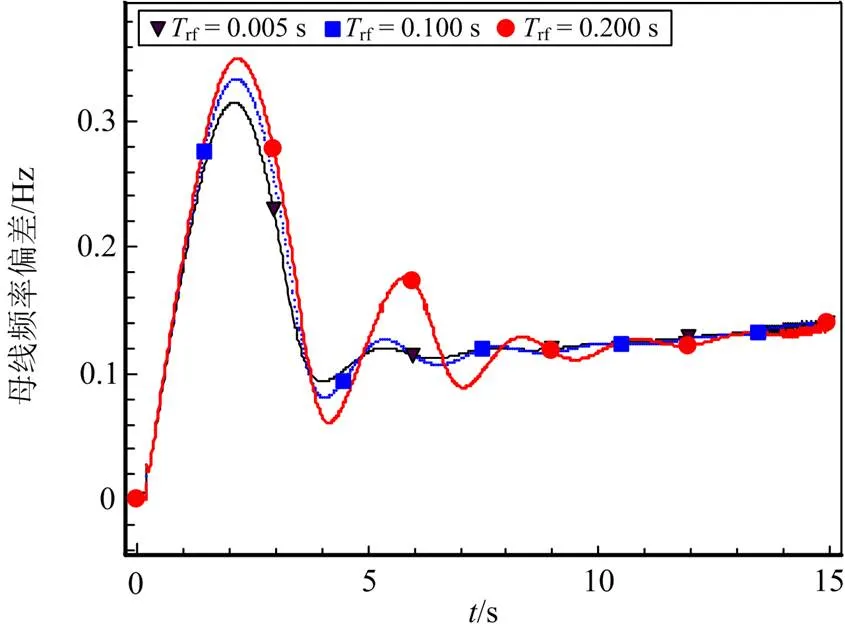
图10 时不同测量时间常数下风机频率偏差曲线

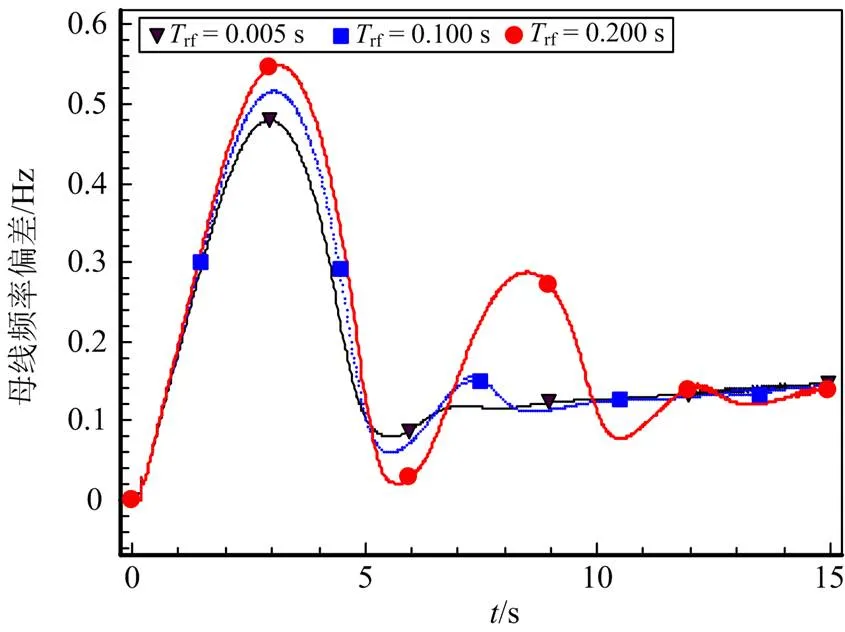
图11 时不同测量时间常数下风机频率偏差曲线

从图10和图11中可以看出，DFIG开始运行的频率为50 Hz，水锤效应时间常数较小时，系统在测量时间常数为0.005 s时的最大频率偏差达到了0.314 Hz，而在测量时间常数为0.200 s时的最大频率偏差达到了0.348 Hz，水锤效应时间常数较大时，系统在测量时间常数为0.005 s时的最大频率偏差达到了0.479 Hz，而在测量时间常数为0.200 s时的最大频率偏差达到了0.552 Hz。从图10和图11中可以看出，随着风机测量时间常数的升高，系统频率偏差随之升高，稳定性变差，振荡幅度增大，且水锤响应时间常数越高越明显。

2.5 负荷模型的影响

为了更好地研究风机并网后对频率特性的影响，本文引入3种云南电网中较为常用的负荷模型进行调频性能的对比，负荷模型1采用30%恒阻抗+30%恒电流+40%恒功率，有功功率因子和无功功率因子分别取1.2和-2.0，常用于电网规划分析计算，以下简称规划模型。负荷模型2根据3类典型高耗能用电设备频率特性因子的分析结果，将有功和无功功率因子均修正为0，以下简称修正规划模型。负荷模型3采用100%恒阻抗和50%感应电动机负荷模型，有功功率因子和无功功率因子也分别取1.2和-2.0，以下简称调度模型。负荷模型参数如附录A中表A1所示。在图3所示系统中，考虑在不同负荷模型下，分析双馈风机采用下垂控制策略参与一次调频时的频率差异，风机频率响应曲线如图12所示。

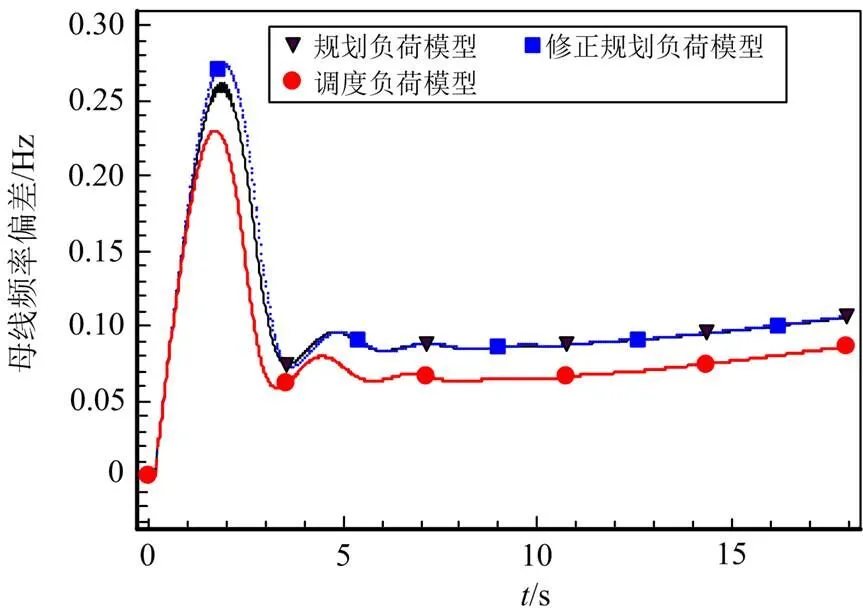
图12 不同负荷模型下的风机频率响应曲线

3 实际电网仿真分析

为了进一步验证风机并网节点频率解析式和影响因素理论分析的正确性，本文在电力系统仿真软件PSD-BPA中搭建异步联网送端云南电网仿真模型。以云南电网中风力发电渗透率较高的大理地区为例，其220 kV及以上主网结构地理接线图如图13所示，参与调频的风电场汇总情况如表3所示。

以楚穗直流发生双极闭锁故障为例，仿真分析关键参数对调频性能的影响。由于在云南电网中水轮机占比较高，水锤效应的影响较大，且负荷模型对频率特性的影响较大，故深入研究和仿真分析水锤效应时间常数和负荷模型对调频性能的影响，并与理论分析结果进行对比，进一步分析双馈风机调频对水锤效应的弥补效果。

图13 大理地区220 kV及以上系统主网架地理接线图

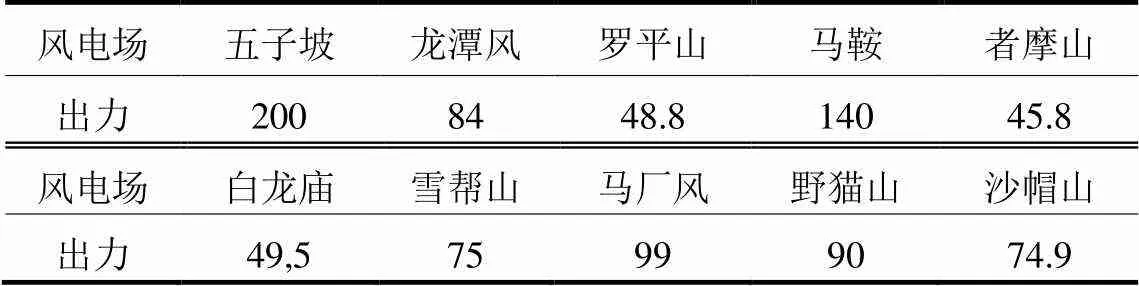
表3 大理地区参与调频风电场汇总表

3.1 水锤效应时间常数的影响

云南电网中，水轮机的占比较大，由于水锤效应的存在，原动机与调速器模型会对系统输出负阻尼，且水锤效应常数w越大，由水锤效应引起的水轮机功率反调现象越明显，负阻尼效应越严重，不利于系统的稳定运行。由式(2)可以发现，水锤效应时间常数是影响水锤效应的关键因素。因此，本节考虑在不同水锤效应时间常数下，以楚穗直流发生双极闭锁故障进行仿真，分析风机并网节点感受到的频率差异以及采用下垂控制策略参与一次调频时的出力变化，马鞍风电场单台风机频率偏差曲线和有功功率响应曲线如图14所示。

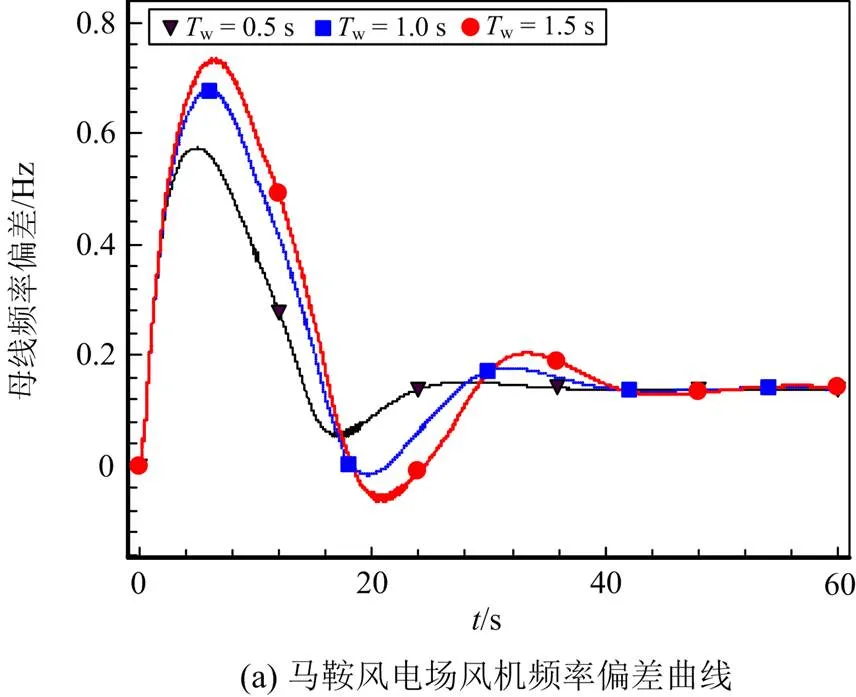
3.2 负荷模型对频率和功率的影响

在水锤效应时间常数取0.5 s的情况下，分析对比不同负荷模型对云南电网调频性能的影响，马鞍风电场单台风机频率偏差曲线和有功功率响应曲线如图15所示。

从图15中可以看出，系统在0.2 s时发生直流闭锁故障，DFIG开始运行的频率为50 Hz，使用规划负荷模型时，系统在4.9 s时的最大频率偏差达到了0.683 Hz，使用修正规划负荷模型时，系统在5.0 s时的最大频率偏差达到了0.729 Hz，使用调度负荷模型时，系统在4.9 s时的最大频率偏差达到了0.573 Hz，DFIG开始运行的有功功率为1.4 MW，使用规划负荷模型时，系统在9.0 s时的有功功率最小值到达0.227 MW，使用修正规划负荷模型时，系统在9.5 s时的有功功率最小值到达0.165 MW，使用调度负荷模型时，系统在8.8 s时的有功功率最小值到达0.255 MW。可见，调度负荷模型相对于规划负荷模型和修正规划负荷模型的调频性能更好，DFIG功率恢复更快。

3.3 风电场参与一次调频的技术指标

为了更好地对调频效果进行量化评估，本文主要选取文献[22-25]中的响应时间、调节时间和最高点频率来衡量调频效果，具体指标定义可查阅文献[22-25]，如图16所示。对图14和图15中所示的频率响应曲线进行量化评估，得到不同水锤效应时间常数和不同负荷模型下的调频指标，如表4所示。

由表4可知，增大水锤效应时间常数将延长响应时间和调节时间，系统响应变慢，系统最高点频率上升，系统调频效果变差。在3种负荷模型中，调度负荷模型的频率偏差最小，从抑制最大频率偏差的角度来看系统调频性能可以得到一定改善，调频效果最优。

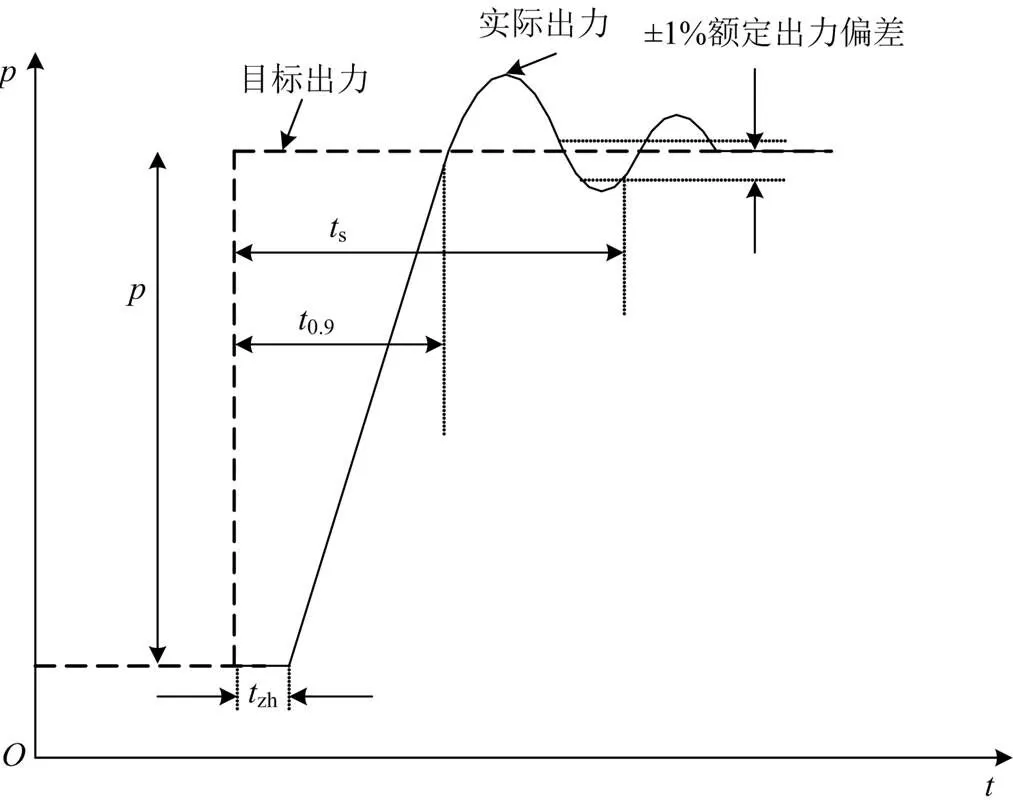
图16 风电场参与调频阶跃扰动过程评价指标示意图

表4 不同参数对调频指标影响对比

4 结论

本文基于直流潮流法，推导了水轮机和风机并网节点频率的解析式，在此基础上对云南电网发生双极闭锁故障时遇到的高频问题进行分析，得出结论如下：

1) 在解析式和仿真验证下得出水锤效应时间常数、惯性环节时间常数、下垂控制系数在参与一次调频后对系统频率的影响，得到3种影响因素对水轮机水锤效应的影响规律，对风电机组的实时投切、风电并网调度具有一定意义。

2) 风机补偿水轮机水锤效应具有一定效果，有效减小水轮机水锤效应导致的反调现象，但受限于风机装机容量、调频控制参数的合理整定以及风机的响应速度。

附录A

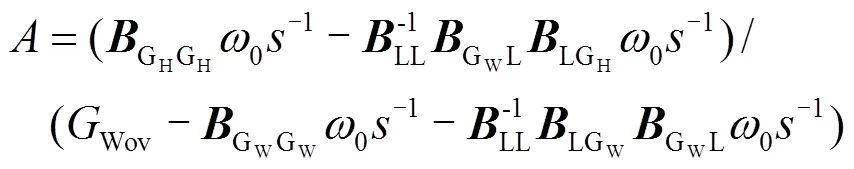
图A1 风机节点频率变化响应随水锤效应时间常数和阶跃扰动变化趋势

Fig. A1 Response of wind turbine node frequency varies with the time constant of water hammer effect and step disturbance

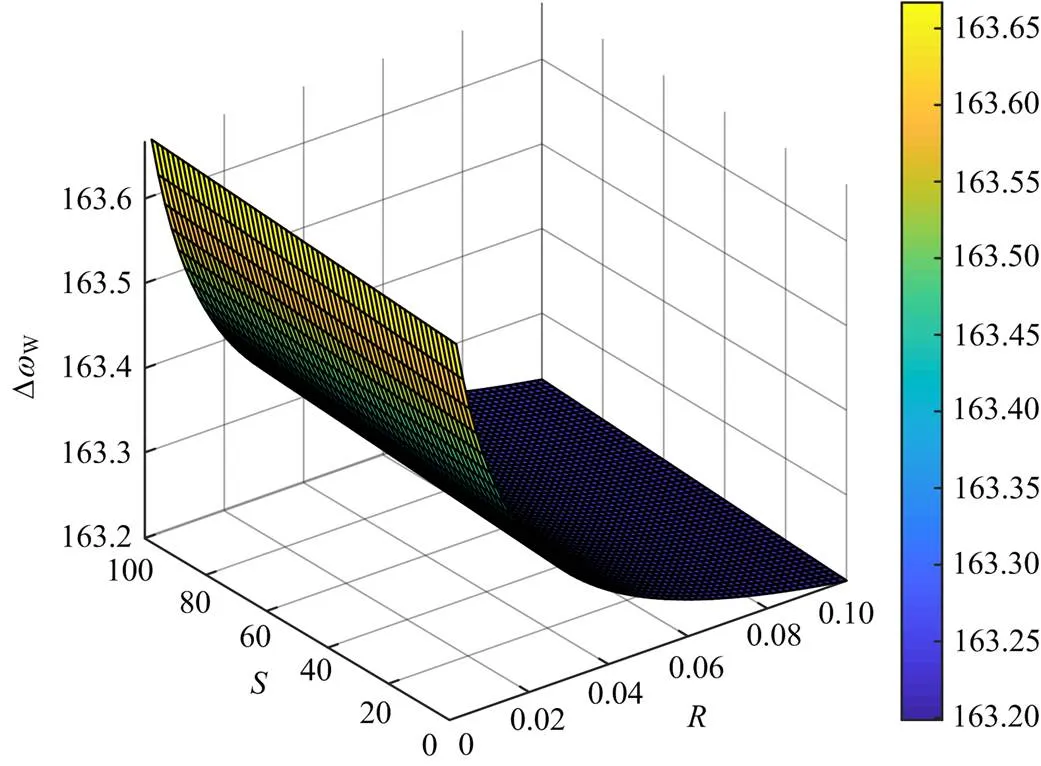
图A2 风机节点频率变化响应随调差系数和阶跃扰动变化趋势

Fig. A2 Response of wind turbine node frequency changes with the adjustment coefficient and step disturbance

图A3 风机节点频率变化响应随软反馈环节系数和阶跃扰动变化趋势

Fig. A3 Variation trend of wind turbine node frequency with soft feedback link coefficient and step disturbance

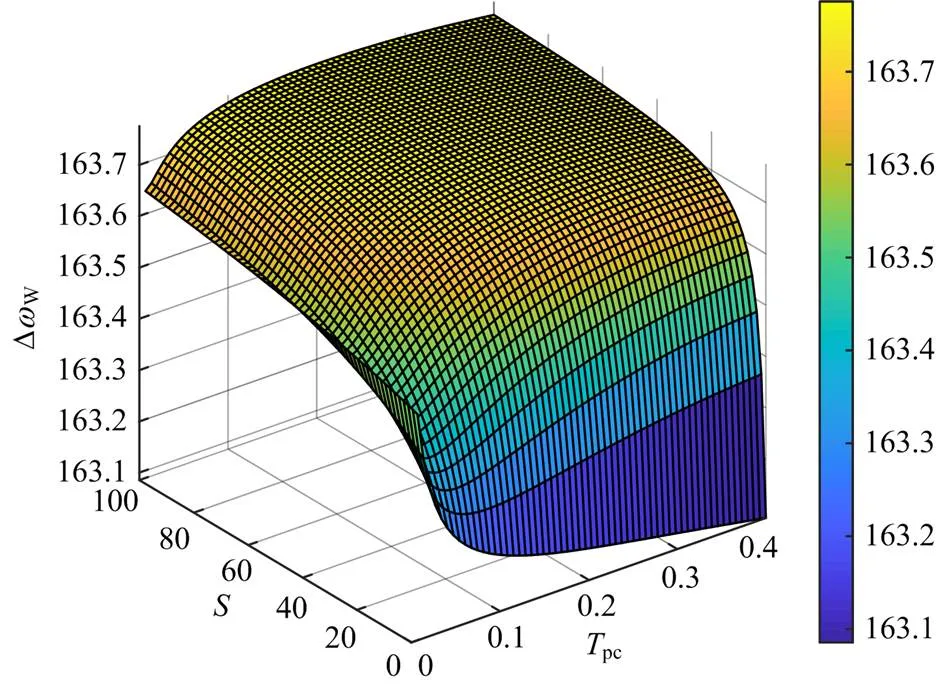
图A4 风机节点频率变化响应随惯性环节时间常数和阶跃扰动变化趋势

Fig. A4 Wind turbine node frequency response varies with time constant and step disturbance

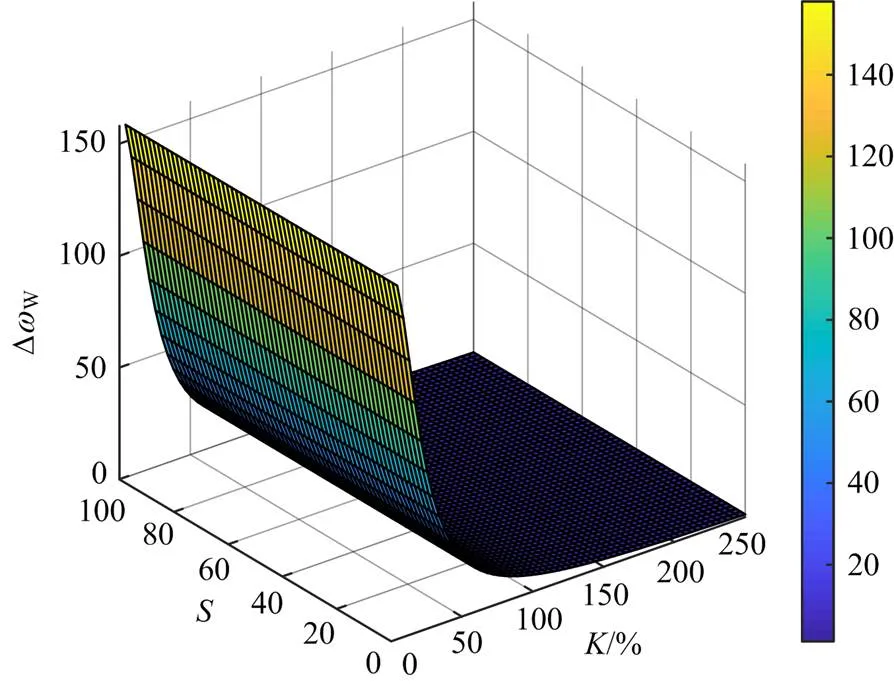
图A5 风机节点频率变化响应随下垂控制系数和阶跃扰动变化趋势

Fig. A5 Response of wind turbine node frequency changes with droop control coefficient and step disturbance

表A1 负荷模型参数

Table A1 Load model parameters

模型名称恒阻抗有功/%恒阻抗无功/%恒电流有功/%恒电流无功/%恒功率有功/%恒功率无功/%有功频率因子无功频率因子马达比例/% 规划模型3030303040401.2-20 修正规划模型303030304040000 调度模型10010000001.2-250

[1] 胥心怡, 武家辉, 姚磊, 等. 基于协同惯量控制的双馈风机并网系统稳定性分析[J]. 电力建设, 2021, 42(12): 59-67.

XU Xinyi, WU Jiahui, YAO Lei, et al. Stability analysis of DFIG grid-connection system applying cooperative inertia control[J]. Electric Power Construction, 2021, 42(12): 59-67.

[2] 杨蕾, 王智超, 周鑫, 等. 大规模双馈风电机组并网频率稳定控制策略[J]. 中国电力, 2021, 54(5): 186-194.

YANG Lei, WANG Zhichao, ZHOU Xin, et al.Frequency stability control strategy for large-scale grid connections with DFIG units[J]. Electric Power, 2021, 54(5): 186-194.

[3] 王中, 黎丽丽, 李振华, 等. 考虑新能源渗透的电网频率概率分布研究[J]. 电力系统保护与控制, 2021, 49(20): 65-73.

WANG Zhong, LI Lili, LI Zhenhua, et al. The evolution characteristics of power grid frequency probability distribution[J]. Power System Protection and Control, 2021, 49(20): 65-73.

[4] 饶成骄. 风电补偿水电系统水锤效应的控制策略及电网频率特性研究[D]. 成都: 西南交通大学, 2018.

RAO Chengjiao. Study on control strategy of wind power compensating for water hammer effect of hydropower system and frequency characteristics of power grids[D]. Chengdu: Southwest Jiaotong University, 2018.

[5] 饶成骄, 郭成, 马宁宁, 等. 考虑水轮机水锤效应的电网频率变化的解析方法[J]. 电网技术, 2018, 42(6): 1892-1898.

RAO Chengjiao, GUO Cheng, MA Ningning, et al. Analytical method of power grid frequency change considering water hammer effect of turbine[J]. Power System Technology, 2018, 42(6): 1892-1898.

[6] 李颖颖, 王德林, 范林源, 等. 双馈风电机组限功率运行下频率稳定的变系数控制策略[J]. 电网技术, 2019, 43(8): 2910-2917.

LI Yingying, WANG Delin, FAN Linyuan, et al. Variable coefficient control strategy for frequency stability of DFIG under power-limited operation[J]. Power System Technology, 2019, 43(8): 2910-2917.

[7] 蔡葆锐, 杨蕾, 黄伟. 基于惯性/下垂控制的变速型风电机组频率协调控制方法[J]. 电力系统保护与控制, 2021, 49(15): 169-177.

CAI Baorui, YANG Lei, HUANG Wei. Frequency coordination control of a variable speed wind turbine based on inertia/droop control[J]. Power System Protection and Control, 2021, 49(15): 169-177.

[8] 颜湘武, 李君岩, 魏星. 直驱永磁同步风电机组在全风速范围内的控制策略研究[J]. 电力系统保护与控制, 2019, 47(23): 138-144.

YAN Xiangwu, LI Junyan, WEI Xing. Research on control strategy of direct-drive permanent magnet synchronous wind turbine in full wind speed range[J]. Power System Protection and Control, 2019, 47(23): 138-144.

[9] 王瑞峰, 高磊, 谌杰, 等. 高风电渗透率下变速风电机组参与系统频率调整策略[J]. 电力系统自动化, 2019, 43(15): 101-108.

WANG Ruifeng, GAO Lei, CHEN Jie, et al. Frequency regulation strategy with participation of variable-speed wind turbines for power system with high wind power penetration[J]. Automation of Electric Power Systems, 2019, 43(15): 101-108.

[10]刘柏私, 汤凡, 余锐, 等. 高比例水电多直流送端电网频率稳定协调控制技术及实践[J]. 电力系统保护与控制, 2021, 49(6): 181-187.

LIU Baisi, TANG Fan, YU Rui, et al. Frequency stability coordination control technology and practice of a multi-DC outgoing power grid with a high proportion of hydropower[J]. Power System Protection and Control, 2021, 49(6): 181-187.

[11] KRPAN M, KUZLE I. Inertial and primary frequency response model of variable speed wind turbines[J]. Journal of Engineering, 2017(13): 844-848.

[12] 范冠男, 刘吉臻, 孟洪民, 等. 电网限负荷条件下风电场一次调频策略[J]. 电网技术, 2016, 40(7): 2030-2037.

FAN Guannan, LIU Jizhen, MENG Hongmin, et al. Primary frequency control strategy for wind farms under output-restricted condition[J]. Power System Technology, 2016, 40(7): 2030-2037.

[13] 张晨曦, 王德林, 马宁宁, 等. 风电场限功率状态下电网旋转备用优化分配[J]. 电力系统自动化, 2017, 41(21): 170-177.

ZHANG Chenxi, WANG Delin, MA Ningning, et al. Optimal dispatch of spinning reserve in power grid under power-limited condition of wind farm[J]. Automation of Electric Power Systems, 2017, 41(21): 170-177.

[14] 杨悦, 王丹, 胡博, 等. 基于改进多智能体Q学习的多源最优联合调频控制策略研究[J]. 电力系统保护与控制, 2022, 50(7): 135-144.

YANG Yue, WANG Dan, HU Bo, et al. Multi-source optimal joint frequency modulation control strategy based on improved multi-agent Q-learning[J]. Power System Protection and Control, 2022, 50(7): 135-144.

[15] 胡泽春, 丁华杰, 孔涛. 风电-抽水蓄能联合日运行优化调度模型[J]. 电力系统自动化, 2012, 36(2): 36-41.

HU Zechun, DING Huajie, KONG Tao. A joint daily operational optimization model for wind power and pumped-storage plant[J]. Automation of Electric Power Systems, 2012, 36(2): 36-41.

[16] GULSHAN S K, NARAYANAN T, ADEFARATI S S. Frequency regularization of a linked wind-diesel system using dual structure fuzzy with ultra-capacitor[J]. Protection and Control of Modern Power Systems, 2022, 7(1): 165-173.

[17] CAMILLE B, LUC G. Adding wind energy to hydropower[J]. Energy Policy, 2002, 30(14): 1279-1284.

[18] DANIEL F A, STEPHANE K, GATEAN L, et al. Operational constraints and economic benefits of wind-hydro hybrid systems analysis of systems in the US/Canada and Russia[C] // European Wind Energy Conference, 2003, Madrid, Spain: 16-19.

[19] 张平. 文山地区电网风水互补特性研究[J]. 云南电力技术, 2017, 45(1): 67-69.

ZHANG Ping. Study on wind power-hydropower complementarity characteristics in Wenshan regional power grid[J]. Yunnan Electric Power Technology, 2017, 45(1): 67-69.

[20] 何永生, 聂金恒, 邱良,等. 云南省风水互补特性分析[J]. 云南电力技术, 2018, 46(6): 36-38.

HE Yongsheng, NIE Jinheng, QIU Liang, et al. Analysis of wind-hydro complementary in Yunnan province[J]. Yunnan Electric Power Technology, 2018, 46(6): 36-38.

[21] 李智, 王德林, 周鑫, 等. 风水互补主导一次调频的旋转备用优化配置[J]. 电工技术, 2020(14): 7-12, 15.

LI Zhi, WANG Delin, ZHOU Xin, et al. Spinning reserve optimizing dispatch of primary frequency regulation dominated by wind power and hydropower complementation[J]. Electrical Engineering, 2020(14): 7-12, 15.

[22] 汪飞. 风电场一次调频控制方法及试验研究[D]. 西安: 西安理工大学, 2018.

WANG Fei. Wind farm primary frequency regulation control method and test study[D]. Xi 'an: Xi 'an University of Technology, 2018.

[23] 万天虎, 汪飞, 张江滨, 等. 风电场一次调频控制方法及试验研究[J]. 电网与清洁能源, 2019, 35(4): 60-65.

WAN Tianhu, WANG Fei, ZHANG Jiangbin, et al. Study on wind farm primary frequency regulation control method and test[J]. Power System and Clean Energy, 2019, 35(4): 60-65.

[24] 苗翯. 大规模风电并网对电力系统频率响应影响的快速评估模型与机理研究[D]. 镇江: 江苏大学, 2018.

MIAO He. Research on fast estimation model and mechanism of power system frequency response integrated with large scale wind farms[D]. Zhenjiang: Jiangsu University, 2018.

[25] 苗翯, 张道农, 翟桂元, 等. 含风电的电力系统频率响应快速评估模型[J]. 农村电气化, 2019(10): 58-63.

MIAO He, ZHANG Daonong, ZHAI Guiyuan, et al. Fast evaluation model of frequency response of power system with wind power[J]. Rural Electrification, 2019(10): 58-63.

[26] 高原, 马宁宁, 王德林, 等. 异步联网下直流频率调制及其参数对送端系统频率的影响[J]. 电力自动化设备, 2019, 39(9): 173-179.

GAO Yuan, MA Ningning, WANG Delin, et al. Impact of DC frequency modulation and modulation parameters on frequency characteristics of sending end in asynchronous interconnected power grid[J]. Electric Power Automation Equipment, 2019, 39(9): 173-179.

Analysis of frequency characteristics of water hammer effect compensated by wind power frequency modulation

ZHU Bo1, SHU Hongchun1, WU Shuijun2, HUANG Kehao1, SUN Shiyun1, DENG Han1

(1. Kunming University of Science and Technology, Kunming 650051, China; 2. Yunnan Electric Power Test & Research Institute (Group) Co., Ltd., Kunming 650217, China)

Water turbines account for a large proportion of energy in the Yunnan power grid. To solve the problem of power inversion caused by the water hammer effect of the turbine, this paper presents an analysis method of compensating the effect by considering the frequency modulation characteristics of wind power. First, a simple systematic mathematical model including wind, water, network and load is established. Then the algebraic differential and systematic network equations corresponding to the hydraulic turbine and its frequency modulation strategy, the wind turbine and its frequency modulation strategy are obtained by the direct current power flow method. Then linearization is carried out. The frequency domain analytical expression of the frequency response of the turbine and wind turbine grid connected nodes under load disturbance is derived. The influence of frequency modulation control parameters on the system frequency is analyzed according to an analytical formula. Finally, the validity and feasibility of the wind turbine compensating the water hammer effect of hydraulic turbine are verified by a simulation analysis of the two-machine system and the actual power grid.

asynchronous networking; wind power FM; water hammer effect; frequency modulation index

10.19783/j.cnki.pspc.220534

国家自然科学基金重点项目资助(52037003)；云南省重大专项资助(202002AF080001)

This work is supported by the Key Project of National Natural Science Foundation of China (No. 52037003).

2022-04-14；

2022-08-31

朱 博(1997—)，男，硕士研究生，研究方向为新能源参与一次调频策略；E-mail: 787538238@qq.com

束洪春(1961—)，男，教授，博士生导师，研究方向为电力系统新型继电保护与故障测距、故障录波、数字信号处理等；E-mail: kmshc@sina.com

吴水军(1980—)，男，通信作者，高级工程师，研究方向为新能源接入对电力系统的影响及新能源并网检测技术研究。E-mail: 237882753@qq.com

(编辑 周金梅)