一类量子负循环码的构造

刘陶然,开晓山

(合肥工业大学 数学学院,安徽 合肥 230601)

20世纪90年代,量子码被证明是克服量子信道干扰最有效的编码方案,能实现量子比特在带有噪音的量子信道上可靠传输。量子码的理论研究的一个核心问题是构造极小距离尽可能大的量子纠错码,构造高纠错性能的量子码是近年来编码理论研究的一个热点。文献[1-4]将复杂的量子纠缠态转化为量子位上出现的几种错误类型,建立了量子纠错码与经典纠错码之间的联系。此后,编码学者们通过有限域上的各种经典码来构造量子码。

Bose-Chaudhuri-Hocquenghem (BCH)码是一类重要的循环码,其主要特点是具有高效的编码与译码算法,且其纠错能力可以通过设计距离来控制,得到了广泛的应用。文献[5]利用BCH码构造量子码,并给出了BCH码是厄米特对偶包含码的充分条件。文献[6]给出有限域Fq2上长为(q2m-1)/(q-1)的BCH码是厄米特对偶包含码的一个充要条件,并且通过厄米特构造法得到了一系列量子码。常循环码是循环码的推广,它既继承了循环码的良好性能,又具有若干新特性。文献[7]给出了常循环BCH码的定义,并在此基础上获得了参数较好的量子码。文献[8]利用常循环码构造了具有较好参数的二元量子码。负循环码是常循环码的1个子类,学者们利用负循环码得到了参数较好的量子码。文献[9]研究了2类负循环对偶包含码,构造了量子码,相比于循环码,负循环获得的量子码具有更好的参数。此后,学者们对一些特定码长的量子常循环码展开研究。文献[10]构造了码长为(q2m-1)/(q-1)的量子负循环码;文献[11]通过厄米特构造法,得到了2类码长为(q+1)(q2+1)/r与(q-1)×

(q2+1)/b的量子常循环码。

受上述工作启发,本文研究有限域Fq2上长为(q4-1)/8的厄米特对偶包含负循环码,其中q≡1 (mod 4),给出这类负循环码分圆陪集的特性,确定这类负循环厄米特对偶包含码的最大设计距离;并利用负循环码构造参数良好的量子码。

1 基础知识

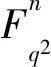
引理1[9]设C为Fq2上长为n的负循环码,其定义集为T,则C⊥h⊆C当且仅当T∩T-q=∅,其中T-q={-qi(mod 2n)|i∈T}。若Tρ=Cb∪Cb+2∪…∪Cb+2(ρ-2)为负循环码C的定义集,其中b是奇数,则称C为设计距离为ρ的负循环BCH码。

引理2[12]Fq2上长为n且设计距离为ρ的负循环BCH码的最小距离为d≥ρ。

设Vn表示n个q维复向量空间Cq的张量积,Vn中每个非零子空间Q称为长为n的q元量子码。设Q的维数为K,称k=logqK为量子码Q的维数。长为n、维数为k、极小距离为d的q元量子码记为[[n,k,d]]。下面的引理3建立了经典纠错码和量子码之间的联系,给出了量子码的一个构造方法。

引理3(厄米特构造法)[4]设C是Fq2上参数为[n,k,d]的厄米特对偶包含码,则由C可以得到参数为[[n,2k-n,d]]的q元量子码。

2 量子负循环码构造

设q为奇素数幂且q≡1(mod 4),下面考虑利用Fq2上码长为n=(q4-1)/8的负循环BCH码来构造q元量子码。首先给出q2模2n的分圆陪集的一些性质。

引理4设n=(q4-1)/8,s=(q2+1)/2,r=(q2-1)/8,则

(1)Ci=Cj当且仅当iq2≡j(mod 2n)或jq2≡i(mod 2n)。

(2)Ci={i}当且仅当i=ks(k=1,3,…,4r-1)。

证明(1) 由ord2n(q2)=2易知,|Ci|至多为2。当i≠j时,Ci=Cj等价于iq2≡j(mod 2n)。又因为iq2·q2=i(q4-1+1)≡i(mod 2n),所以iq2≡j(mod 2n)等价于iq4≡i≡jq2(mod 2n)。

(2) 对于i∈T,Ci={i}当且仅当iq2≡i(mod 2n)⟺i(q2-1)≡0(mod 2n)。因此s整除2i。注意到s是奇数,故s整除i。设i=ks,由i∈T可得:1≤k≤4r-1且k为奇数。由此得出结论。

下面讨论Fq2上长为n=(q4-1)/8的厄米特对偶包含负循环码存在的充要条件,给出它们最大的设计距离。

证明先证充分性。采用反证法,假设C⊥h⊆/C,由引理1知T∩T-q≠∅。因此,存在2个整数h、k,1≤h、k<δM,使得：

2k-1≡-(2h-1)q2j+1(mod 2n)

(1)

其中,j=0,1。当j=0时,(1)式等价于(2k-1)+(2h-1)q≡0(mod 2n)。

注意到:

由此得出矛盾。

当j=1时,(1)式即为：

2k-1≡-(2h-1)q3(mod 2n)。

因为q4≡1(mod 2n),所以该式等价于(2k-1)q≡-(2h-1)(mod 2n),类似于情况j=0,可以得出矛盾。因此C⊥h⊆C。

再证必要性。假设δ>δM,因为-q(2δM+1)≡(q3-q2-3q-1)/4(mod2n),所以(q3-q2-3q-1)/4∈-qC2δM-1。但是δM>(q3-q2-3q+3)/8,因此有T∩T-q≠∅。由引理1知,C⊥h⊆/C。因此1≤δ≤δM。

引理5 设s=(q2+1)/2,r=(q2-1)/8。对任意i∈{1,3,…,2n-1},Ci可以表示为{ks-2rα,ks+2rα},其中,k、α满足下列情况之一:

(1)k∈{1,3,…,2r-1},α∈{0,1,…,2k}。

(2)k∈{2r+1,2r+3,…,4r-1},α∈{0,1,…,2r-1}。

证明对任意i∈{1,3,…,2n-1},由带余除法知,存在整数u、v,使得i=2ur+v,其中:u∈{0,1,…,q2};v∈{1,3,…,2r-1}。于是有：

iq2≡2urq2+vq2≡-2ur+vq2(mod 2n)。

下面分2种情况讨论:

(1) 当0≤u≤4v时,有

0

注意到：

i=2ur+v=vs+(u-2v)2r,

-2ur+vq2=vs-(u-2v)2r,

令k=v,α=u-2v,则

Ci={ks-2rα,ks+2rα},

其中:k∈{1,3,…,2r-1};α∈{0,1,…,2k}。

(2) 当4v+1≤u≤q2时,有

-2n<-2ur+vq2≤-2r(4v+1)+

vq2=v-2r<0。

注意到i=(v+2r)s+(u-2v-4r-1)2r,-2ur+vq2=(v+2r)s-(u-2v-4r-1)2r,令k=v+2r,α=u-2v-4r-1,则

Ci={ks-2rα,ks+2rα},

其中:k∈{2r+1,…,4r-1};α∈{2k-8r,…,8r-2k}。

由Ci中元素的对称性可得α∈{0,1,…,8r-2k}。

(1)k为奇数且1≤k≤2λ-1,0≤α≤2k。

通过引理6,可以计算定义集T中满足条件1≤i

T(δ)=-8λ2+18λ-5+(λ-1)×

(2)

证明当λ≥1时,在引理6的情况(1)中,组成T的分圆陪集中单元素集有λ个,故满足情况(1)条件的元素数目为3+(4λ-1)/2·λ·2-λ=4λ2+λ。

情况(2)中组成T的分圆陪集中单元素集有(λ-1)个。注意到:

满足情况(2)的元素数目为:

(λ-1)(5-12λ)。

两者相加即得等式(2)。当λ=0时,不存在满足引理6的分圆陪集的单元素集,此时T(δ)=0。综上,得到结论。

现在可以确定定理1中负循环BCH码的维数,进而利用厄米特构造法得到量子码。

证明由定理1知,C是厄米特对偶包含码。由引理7知,dim(C)=n-(2δ-T(δ))=n-2δ+T(δ)。再由引理2知,d(C)≥δ+1。因此,C是参数为[n,n-2δ+T(δ),≥δ+1]的厄米特对偶包含码。根据引理3,由C可以得到参数为[[n,n-4δ+2T(δ),≥δ+1]]的q元量子码。

例1 当q=5时,根据定理2,可以得到参数如下的五元量子码:

[[78,78-4δ,≥δ+1]],1≤δ≤6;

[[78,78-4δ+2,≥δ+1]],7≤δ≤8;

[[78,78-4δ+6,≥δ+1]],10≤δ≤11。

当7≤δ≤12时,文献[13]中量子码的参数为[[78,78-4δ,≥δ+1]]。显然,定理2得到的量子码均优于码表中所给的量子码;同时也得到一个新的五元量子码[[78,36,≥14]]。

3 结 论

本文研究了Fq2上的长为n=(q4-1)/8的负循环码,其中q≡1(mod 4),通过研究分圆陪集的性质,得到设计距离δ的负循环码为厄米特对偶包含码的一个充要条件;进一步确定了厄米特对偶包含负循环码的确切维数,并由此构造了参数良好的量子码。一个值得探讨的问题是利用其他类型的常循环码构造参数优良的量子码。