面向管材存储的自动化立体仓库货位优化
屈新怀,纪 飞,丁必荣,孟冠军
(合肥工业大学 机械工程学院,安徽 合肥 230009)
0 引 言
自动化立体仓库(automated storage and retrieval system,AS/RS)是现代仓储技术、计算机技术和自动化技术高度集成的产物。它能够加快货物流转,缩短生产周期,进而降低企业制造成本,是各类制造企业向着智能化转型不可或缺的仓储形式[1]。同时,汽车制管厂作为车企的一个重要组成部分,其主要职能是为各类汽车提供各类管材,如制动管路、动力转向管路、燃油管路、空调管路等。由于管材的种类多、尺寸长、致使存储困难,因此将汽车制管厂仓库改造为AS/RS是车企向智能化转型的一个重要步骤。
在AS/RS的研究中,货位优化是影响其性能的一个关键因素[2]。文献[3]面向船舶行业,提出了一种以出库效率、货架稳定性、巷道负载均衡为目标的货位优化模型;文献[4]对于电子产品的存储,建立了一种以提高堆垛机存取效率和货架稳定性为目标的货位优化模型;文献[5]基于液压元器件的存储,考虑了货架稳定性、平衡性和出库效率,建立了货位优化模型;文献[6]基于防洪物资及其存储特点,建立了反映检索效率和货架稳定性为目标的货位优化模型。
结合上述文献可以看出,目前国内外对货位优化方面的研究主要集中在尺寸较短同时包装成块状的材料,并且货架主要是单元格式货架。对尺寸较长的管材和适合存放管材的悬臂式货架[7]的研究很少。因此,本文基于悬臂式货架进行管材的货位优化,从存取效率、货架稳定性和货架平衡性出发建立货位优化问题的数学模型,进一步设计求解该模型的启发式算法,并采用某汽车制管厂的数据进行实例仿真。
1 问题描述
根据管材尺寸较长、种类较多、质量不一的特点,采用悬臂式货架进行存放,构建出AS/RS立面示意图,如图1所示。堆垛机从出入口(I/O)出发,可沿X、Y、Z方向进行作业并沿原路径返回,其中X、Y、Z分别代表货架的排方向、列方向、层方向。
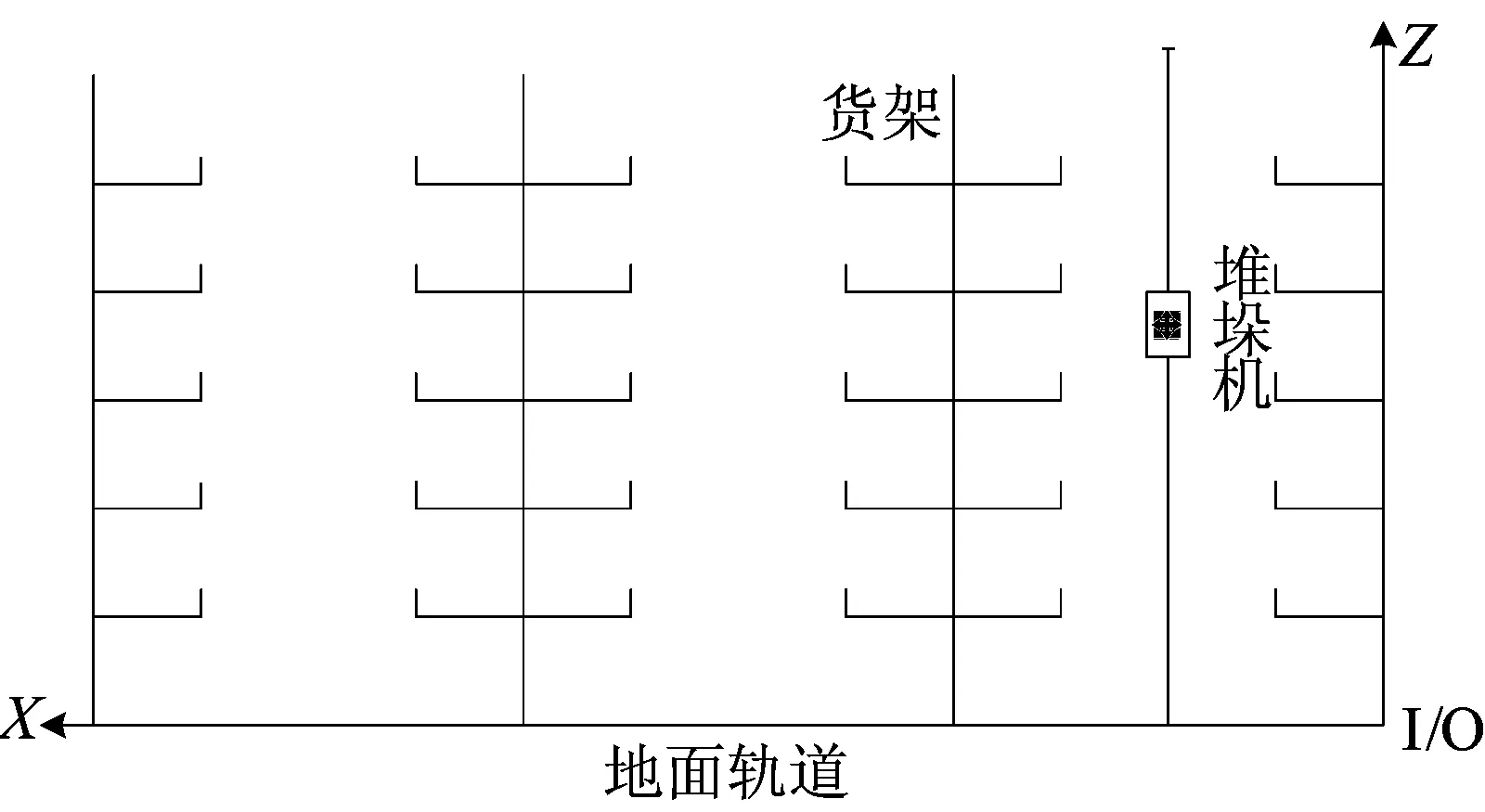
图1 AS/RS立面示意图
为了提高AS/RS的存储效率,保证其货位分配的合理性和安全性,需要使用恰当的货位分配原则,因此提出了以下货位分配的优化原则:
(1) 存取效率原则。将周转率较高的管材放置在离出入口较近的位置,以减少堆垛机行程,从而提高AS/RS的存取效率。
(2) 稳定性原则。将质量较大的管材放置在货架的低层,将质量较小的管材放置在货架的高层,从而降低货架的整体重心。
(3) 平衡性原则。考虑管材的质量和悬梁臂货架的结构特点,需要考虑货架的平衡性,以保证AS/RS具有足够的安全系数[8]。
为了方便AS/RS模型构建和问题研究,基本假设如下:
(1) 仓库只有1个出入库端口,堆垛机只进行单一作业。
(2) 堆垛机匀速运行,不考虑加减速,不考虑堆垛机存取货物的时间,不考虑堆垛机与运输设备的交接时间。
(3) 每个货位只存放1种管材,且货位与管材尺寸相匹配。
2 AS/RS货位优化模型建立
2.1 模型参数
货物位置采用三维坐标(x,y,z)表示,即货物在仓库的第x排y列z层。仓库沿X方向共有a排,沿Y方向共有b列,沿Z方向共有c层。设定堆垛机沿X方向的速度为vx,沿Y方向的速度为vy,沿Z方向的速度为vz;单位货格沿X方向的长度为l,沿Y方向的宽度为w,沿Z方向的高度为h;货架之间巷道的宽度为L;货位(x,y,z)上货物的质量为mxyz,周转率为pxyz,决策变量为dxyz,即当货位(x,y,z)上有货物时dxyz为1,否则为0。
2.2 多目标货位优化模型建立
根据管材和悬臂式货架的结构特点,同时结合上文提出的货物的存取效率、货架的稳定性和平衡性3个货位分配原则,建立多目标货位优化模型。
2.2.1 提高存取效率
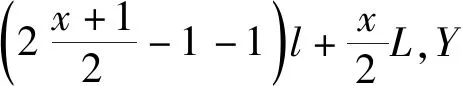
(1)
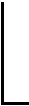
2.2.2 提高货架稳定性
采用上轻下重的原则存放货物以降低货架的整体重心,从而提高货架的稳定性,其数学模型可描述为:
(2)
2.2.3 提高货架平衡性
基于货物载荷和悬梁臂式货架的结构特点,应该尽量使货架两侧载荷均衡,以提高货架的平衡性,其数学模型可描述为:
minf3=
(3)
2.3 权重系数分配
通过赋予权重系数,可以将复杂的多目标函数优化问题转化为单目标函数优化问题,以便于求解。由于3个目标函数的量纲不一致,在分配权重系数前先采用反正切函数转换法对3个目标函数做归一化处理,得到minf1′、minf2′、minf3′,则单目标数学模型可描述为:
minf=w1minf1′+w2minf2′+w3minf3′;
s.t.w1+w2+w3=1,
0≤w1≤1,
0≤w2≤1,
0≤w3≤1
(4)
权重系数w1、w2、w3的取值采用层次分析法[9]确定,经过分析设定判断矩阵为:

求解得到3个目标函数的权重系数分别为0.17、0.63、0.20,最终获得的单目标数学模型可描述为:
minf=
0.17minf1′+0.63minf2′+0.20minf3′
(5)
3 货位优化算法设计
传统粒子群算法(particle swarm optimization,PSO)仅需速度和位置的迭代进化就可以逼近全局最优解,其原理简单且运行高效,比较适合求解本文的货位优化问题,文献[10-11]均采用了PSO进行货位优化方面的研究,并且通过实验取得了良好的优化结果。传统PSO中粒子i的迭代过程可描述为:
(6)
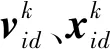
同样广泛应用于自动化立体仓库货位优化问题的还有全局寻优能力强、鲁棒性高的遗传算法(genetic algorithm,GA)。
但是考虑到PSO搜索精度不高、局部搜索能力差且易陷入局部最优的缺陷[12]以及GA收敛速度慢、控制变量多、易早熟的问题,本文构建了PSO与GA的混合算法,即粒子群遗传算法(PSOGA),进行货位优化分析。
PSOGA通过将GA算法中合适的变异算子、交叉算子与PSO算法相结合[13],可以保证种群中个体的多样性,扩展算法的搜索范围,从而增强PSOGA的局部搜索能力,并在一定程度上提高解的质量。PSOGA的具体实现流程如图2所示。

图2 PSOGA流程
PSOGA的具体实现步骤如下:
(1) 将需要入库的货物看作一个个粒子,对其随机分配初始货位并给予初始速度,形成初始种群,每个带有位置和速度信息的粒子作为种群的个体。
(2) 以(5)式作为适应度评价函数,计算种群中各个体的适应度值,选出个体最优和全局最优。
(3) 以(6)式作为迭代公式,更新种群中个体的位置和速度,选出新的个体最优和全局最优。
(4) 对迭代更新后的种群执行GA中的选择、交叉、变异操作。其中选择操作采用锦标赛选择法,交叉操作采用两点交叉,变异操作选取逆转变异算子。
(5) 重新根据(5)式计算适应度值,并判断是否满足终止条件;满足则接受当前解,并获取货位优化后仓库的信息,不满足则循环以上操作。
4 实例计算与仿真分析
以某汽车品牌制管厂仓库的实例数据进行仿真分析,仓库的基本参数信息见表1所列。

表1 仓库基本参数
选取16种不同的管材进行货位优化分析,管材基本信息见表2所列。
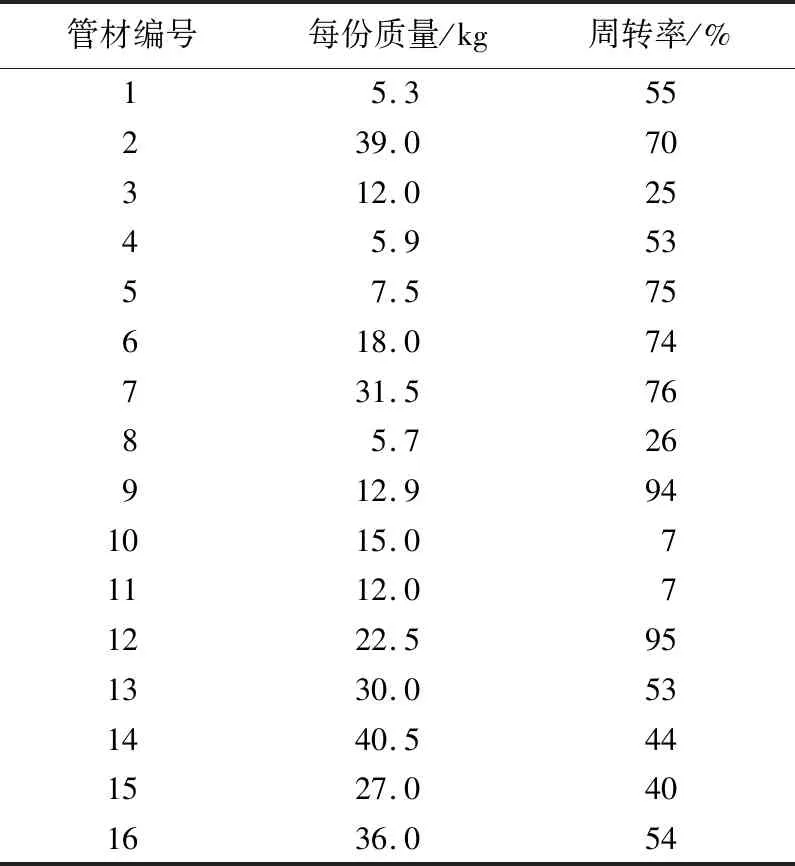
表2 管材数据信息
经过分析比较设定PSOGA中的参数为:加速度常数c1=c2=1;r1、r2选取0~1之间的随机数;惯性权重α采用线性递减权值法确定,最大值和最小值分别设定为1.0和0.8;种群数量为50;迭代次数N为200;选择概率为0.8;变异概率为0.1。
第i次迭代的惯性权重α可描述为:
(7)
使用MATLAB分别运行GA、PSO、PSOGA算法,求解得到的具体目标函数值见表3所列,同时得到3种算法迭代收敛的对比结果,如图3所示。
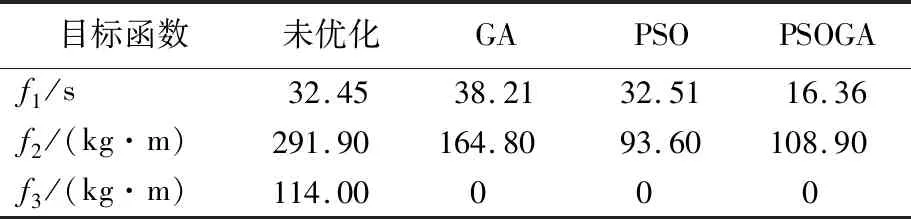
表3 目标函数值优化结果对比
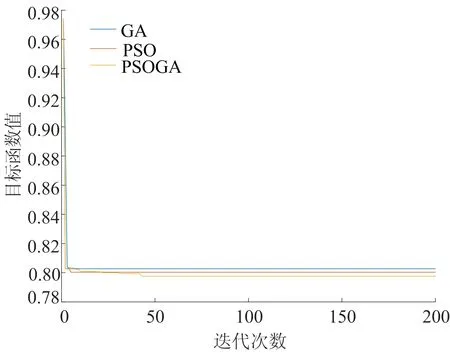
图3 3种算法迭代收敛对比结果
观察表3数据可以看出,相较于未优化前,经过3种算法优化后的目标函数值在货架的平衡性和稳定性上均有大幅度提升,但在存取效率方面,GA和PSO的优化并不理想,只有PSOGA具有较好的优化结果;同时结合图3的迭代收敛对比结果可以发现,PSOGA虽然收敛稍慢,但其归一化后的总目标函数值小于其余2种算法,即解的综合质量高于GA和PSO算法,且不易陷入局部最优。因此选用PSOGA进行货位优化具有一定的优越性。
PSOGA算法优化前、后仓库的货位分配示意图如图4所示。
分析计算表3数据可得,相较于未优化前,经PSOGA优化后存取效率提高49.58%,货架稳定性提高62.69%,货架平衡性提高100%。从图4可以看出,经PSOGA优化后的货位分配明显更加合理。
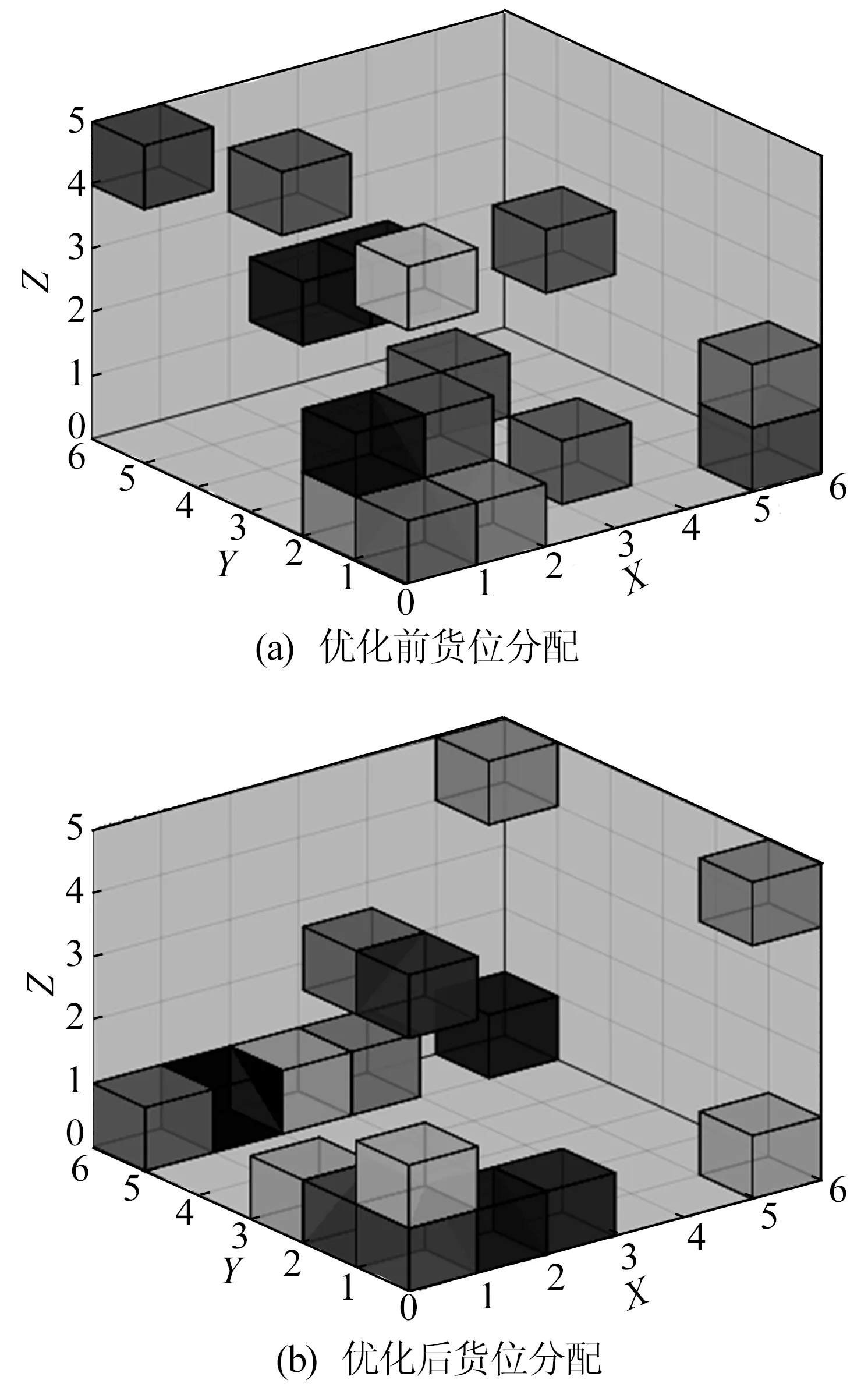
图4 PSOGA优化前、后货位分配图
5 结 论
本文面向管材存储构建了AS/RS模型研究货位优化问题。根据管材特点采用悬臂式货架进行存储并选取了合适的货位分配策略和原则,建立了货位优化的多目标数学模型;通过MATLAB编程并采用PSOGA求解,获得了全局最优解。结果表明,本文方法有效且切实可行,能够较全面地提高仓库的存取效率、货架稳定性和平衡性。本文对面向管材存储的AS/RS研究具有一定的理论和实践意义。

