贝尔数理论推导与实际应用问题的分析研究

苏德照 岑 岚 黄 艳 杨承涛 钟春坚

1.百色学院数学与统计学院 广西百色 533000；2.百色学院教育科学学院 广西百色 533000

贝尔数是用在组合数学中的一组整数数列构成，是以埃里克坦普尔贝尔而命名的[1]。杨胜彬等[2]2015年为建筑工程总公司对基站建设方案进行研究，采用随机穷举算法探索出了最优化的污水处理站建设方法，将贝尔集合划分运用到实际问题中去。付秋菊[3]2019年以代数的视角来研究并探索集分类的问题，具体来说，就是在有限域上成立了一个能够把所有集合都划分在零维仿射代数上的映射，并且对这些映射的代数性质进行深入研究。王爽[1]2012年系统研究Stirling变换公式在Bell多项式与错排多项式、调和数中的运用。我们基于贝尔数各类的函数关系式和递推公式，对贝尔数理论进行推导和贝尔数与集合划分的进行实际应用问题研究，结合三种度量进行研究。

一、贝尔数定义及其理论推导

(一)贝尔数定义

在组合数学里，将一个n元集合划分的组合总个数称为贝尔数，记作为Bn；设n元集合的所有贝尔划分集合为B(n)。集合S的另一个重要划分概念是将集合S划分成非空子集且两两互不相交的并集[3]，B0是1。

(二)贝尔数的推导规律

由它的集合划分可以总结出一些结论：

当n=1时，第一列第一项的贝尔数为a(1，1)=1；

当n>1时，第n行第一项的贝尔数为a(n，1)=a(n-1，n-1)；

当n>1，m>1时，则有第n行第m项的数值为a(n，m)=a(n-1，m-1)+a(n，m-1)。

由上述结论得出的结果，将所得到的数值绘制成数表(结果见表1)，称为L型贝尔数运算表，由于此运算方式与L类似将其定义为L型运算，该数表每行的首项为贝尔数[4]。

表1 L型贝尔数运算表

(三)贝尔数适用的递推公式及证明

证明：由于Bn+1是含有n+1个元素的集合划分个数，设Dn的集合为{b1，b2，...，bn}，Dn+1的集合为{b1，b2，…，bn，bn+1}，那么可以认为集合Dn+1是在集合Dn的基础上添加一个元素bn+1产生的，接下来可以单独考虑第bn+1个元素。

(1)可以假设当bn+1元素被单独分配到一类时，剩下有n个元素，所以在这种情形下有(nn)Bn划分个数；

(2)可以假设当bn+1元素和剩余的n个元素中的一个元素划分为一类时，那么还剩下n-1个元素，这种情形下有(nn-1)Bn-1划分个数；

(3)可以假设当bn+1元素和剩余的n个元素中的两个元素划分为一类时，那么还剩下n-2个元素，这种情形下有(nn-2)Bn-2划分个数；

任意的贝尔数都是对应“第二类Stirling数[1，3]”的和。

二、豪斯多夫距离的基本原理

豪斯多夫距离是匹配二点特征的一个距离方式，它并不要求建立点和点间的一一对应关系，仅要求算出这两个点集间的相似度(或最大距离)，从而能够更高效地处理一般特征点的情况[5]。

把距离函数定义成两个空间的距离推测，目的是描述两个有限封闭的集合之间的相似度的一种度量。以下是对豪斯多夫距离的定义：

定义2.1 假设该空间上存在有两个点集A和B，那么H(A，B)表示集合A与集合B之间的豪斯多夫距离，则其数学定义为H(A，B)=max(h(A，B)，h(B，A))。为A集合与B集合间的双向豪斯多夫距离[5-6]。

范数是对函数、向量和矩阵定义的一种度量形式，同时也是数学中的一种基本概念。其在泛函分析中，它定义在赋范线性空间中，并需要满足一定的条件，即①非负性：||x||≥0且||x||=0⟺x=0；②齐次性：||cx||=|c|||x||；③次可加性：||x+y||≤||x||+||y||。范数经常被用来度量某一个向量空间(或矩阵)中的每一个向量的长度或者大小。上述的||·||称为x上的一个范数。

三、三种度量方法介绍

在论文中用N来代表每个自然数的集合，用R表示每个实数值的集合，用R+代表每个正实数值的集合。对所有集合，用|A|表示该集合的基数，P(A)表示该集合的幂集[7]，幂集是原集合中所有的子集(其中也包括全集和空集)所构成的集合族。

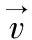
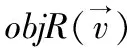
(一)三种度量定义及介绍

度量很好地继承了数学中的公理化性质和测量点或结构距离的直观性质。在这里介绍各种度量，以进一步设计统计机制。

秩度量的应用相对是比较容易，但由于它过于简单，而且主要取决于对分区组进行排序的要求，在某些数据类型中，有可能无法满足这一要求。为了克服这一缺点，可以通过豪斯多夫度量和改进后的豪斯多夫度量来实现。现在来介绍这两个度量。

设α：S×S→R为距离函数，其中S⊆N为有限集。设GOα(或α：S×S)表示α的距离矩阵。设B(S)是S的所有贝尔划分的集合。设∀P，Q∈D(S)，∀p∈P，∀q∈Q，其中P表示划分矩阵行，Q表示划分矩阵列。定义距离矩阵行式最小值查找函数为Cn(p，Q)=min{α(p，q)，qQ}，即为了寻找出每个集合划分的距离矩阵的每一行最小值；定义距离矩阵列式最小值查找函数为Cm(P，q)=min{α(p，q)，pP}，即为了寻找出每个集合划分的距离矩阵的每一列最小值。定义行式最小值中的最大值查找函数FCn(P，Q)=max{Cn(p，Q)，pP}，即是寻找出所有行中最小值中的最大值。定义列式最小值中的最大值查找函数FCm(P，Q)=max{Cm(P，q)，qQ}，即是寻找出所有列中最小值中的最大值。定义行式最小值中的平均值查找函数即是寻找出所有行中最小值中的平均值。定义列式最小值中的平均值查找函数即是寻找出所有列的最小值中的平均值。

基于定义2.1和定义2.2有如下定义。

定义3.2(豪斯多夫度量[5-6])由dF：P(S)×P(S)→N，有dF(P，Q)=max{FCn(P，Q)，FCm(P，Q)}，用GOF来表示其相关的距离矩阵。

定义3.3(改进后的豪斯多夫度量[5-6])由dA：P(S)×P(S)→R，有dA(P，Q)=max{ACn(P，Q)，ACm(P，Q)，用GOA表示其相关的距离矩阵。

(二)三种度量标准和范数定义及介绍

根据上述定义的度量，下面将设计能够反映出客观性转换程度的相应度量标准和范数。

定义3.5(秩度量标准)由定义3.1(秩度量)得到:

当且仅当|P∪Q|=1且drm(P，Q)=0时，分母等于0，默认它是忠实地转换的，因此该定义是合理的。以下定义同理。

定义3.6(秩度量范数)对于Hr*：D(S)→R+，有Hr*(I)=∑PI∑QIHr(P，Q)。

如果对分母进行分析，就会发现它代表了客观性心理过程之前的结构距离，分子表示处理后的主观性,这个比率揭示了主观性相对于客观性的相对程度。以下定义同理。

定义3.7(豪斯多夫度量标准)由定义3.2(豪斯多夫度量)得到：

定义3.8(豪斯多夫度量范数)对于HF*：D(S)→R+，有HF*(I)=∑PI∑QIHF(P，Q)。

定义3.9(改进后的豪斯多夫度量标准)由定义3.3(改进后的豪斯多夫度量)得到

定义3.10(改进后的豪斯多夫度量范数)对于HA*：D(S)→R+，有HA*(I)=∑PI∑QIHA(P，Q)。

(三)分区指标定义及介绍

设∀E，F∈B(S)，基于上述定义，设计了以下分区度量。

定义3.11(秩度量分区)有Tr：B(S)×B(S)→R，得到Tr(E，F)=|Hr*(E)-Hr*(F)|。

定义3.12(豪斯多夫度量分区)有TF：B(S)×B(S)→R，得到TF(E，F)=|HF*(E)-HF*(F)|。

定义3.13(改进后的豪斯多夫度量分区)有TA：B(S)×B(S)→R，得到TA(E，F)=|HA*(E)-HA*(F)|。

以上分区(划分)均基于绝对值度量。

四、度量在实际问题中应用

论文主要利用三种度量进行客观性和主观性机理转换，该论文旨在客观性到主观性的转换机制，主要利用集合划分的概念进行引入，可以模拟得到客观性到主观性的转换中应用该划分。下面对于高中学生考试成绩的客观性预测评估，在此已知该次考试的分数区间为[0，150]，根据新课改政策的要求，可以将各个学科考试成绩分为5个等级，即为A等[127.5，150]、B等[105，127.5)、C等[90，105)、D等[60，90)、E等[0，60)。

现假如八名学生是通过正常排序行为感知客观性，即根据正态分布进行排序，评估结果是由该名学生平时表现客观性评价得出，那么八名学生对另一名学生的某一次考试成绩进行分数评估结果，具体结果详见表2。

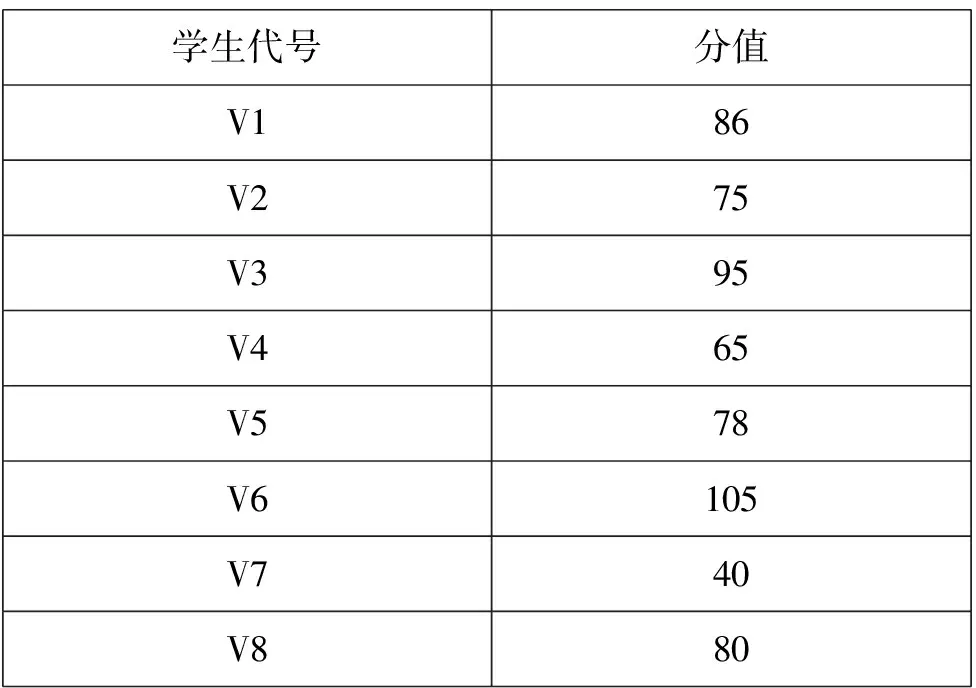
表2 八名学生对另一名学生的某一次考试成绩分数评估

(一)三种度量的实际应用

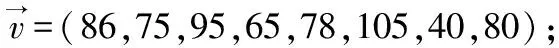
表3 客观性相关距离相关矩阵

表4 由度量产生的相关距离矩阵

(二)度量标准和范数的实际应用

1.三种度量标准的应用

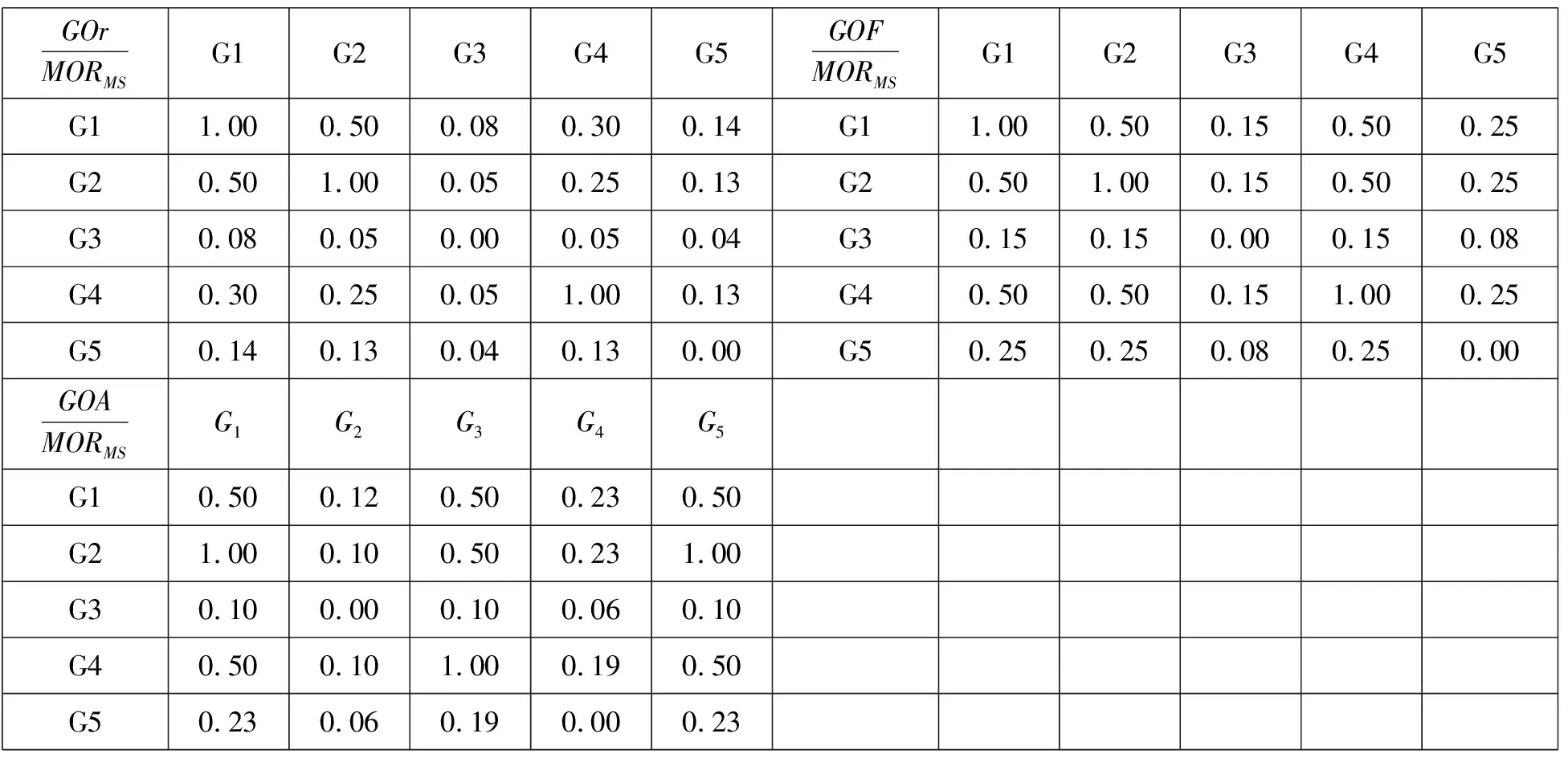
表5 由度量标准产生的相关距离矩阵

2.三种度量范数的应用

由秩度量范数求得结果为6.32；由豪斯多夫度量范数求得结果为8.56；由改进后的豪斯多夫度量范数求得结果为8.04。

(三)统计检验

1.W检验

由相关距离矩阵GOr、MORMS数据检验得到p-value=0.0255、0.0135<0.05，说明数据正态性比较差；由相关距离矩阵GOF、GOA数据检验得到p-value=0.0957、0.0614>0.05，说明数据服从正态分布的特征，数据正态性较好。

2.卡方检验

通过对三个度量产生的相关距离矩阵(GOr、GOF、GOA)的数据进行双尾检验，选择通过显著性水平为5%，卡方检验结果详见表6。由检验结果得出以下结论，如果采用秩度量，则会拒接原假设；如果采用豪斯多夫度量和改进后的豪斯多夫度量，则会接受零假设。说明了采用豪斯多夫度量和改进后的豪斯多夫度量得到的结果与主观性具有一致性，并同时说明方法具有可行性。

表6 双尾检验95%置信区间、方差、p-value

五、说明

(1)首先假设受试者具有随机性，由受试者得到的数据具有可用性。

(2)假设客观状态到主观状态的心理转换是基于给定数据的正态分布，在后续产生的相关距离矩阵进行正态分布检验(W检验)，在一定程度上保证了数据的正态性。

(4)当从客观性到主观性的转换用整数来近似时，如果一个人的自身能力能够处理更精细的结果，那么得到的数据将更加符合受试者的意愿，可以采用更细的标度，从而客观性转换也可以提高精确度。

(5)在进行非参数测试时，通过参数限制样本空间。考虑的贝尔分区只是一部分，并限制在带有固定类别(组)的贝尔分区的子类别。

结语

由于学生每次考试成绩是受多方面因素影响，在学生考试成绩的预估中，由检验结果可以得出以下结论。如果采用秩度量，则会拒接原假设；如果采用豪斯多夫度量和改进后的豪斯多夫度量，则会接受零假设。说明在客观性和主观性进行机理转换中，采用豪斯多夫度量和改进后的豪斯多夫度量可以很好地将客观性转换到主观性，可以预估出学生主观性的猜测。该方法还可以将应用于其他领域进行研究，比如经济领域、投资领域等。

致谢:感谢百色学院数学与统计学院陈瑞明老师对本文的指导!