幂等算子核空间上的投影

刘 妮,任谨慎,冯军庆，郑 芳

(空军工程大学 基础部,西安 710051)

1 幂等算子概述

设H与K为无限(可分)复 Hilbert 空间,B(H,K)为H到K上全体有界线性算子之集，H=K时记作B(H).若F∈B(H)且满足F2=F,则称F是幂等的，用Θ(H)表示H中幂等算子的集合.幂等算子F若满足F=F*，则F为正交投影.对H的闭子空间M，用PM表示M上的正交投影.特别地,若F∈Θ(H),注意到R(F)=ker(I-F)，因此R(F)为H的闭子空间，用PF,PN(F)分别表示F的值域R(F)及核空间N(F)上的正交投影.B(H)中满足V*V=VV*=I的算子V称为酉算子，F*为F的伴随,σ(F)为F的谱.

幂等算子在统计学、量子信息及经济学领域都有着较为广泛的应用，是算子论中最基本也较为特殊的一类算子.近年来关于幂等算子的可逆性、几何结构等都吸引了国内外学者的研究[1-2]，文献[3-5]研究了幂等算子的J-正(负,压缩,扩张)的存在性、性质以及幂等算子的表示.文献[6]中作者借助矩阵分块技巧讨论了Hilbert空间上特殊的幂等算子类.文献[7-8]利用幂等算子F值域及空间上的正交投影PF,PN(F)对幂等算子进行了刻画，即F=PF(PF+PN(F))-1，并进一步给出了F的范数的表示.本文在此基础上借助算子分块技巧，对幂等算子核空间及值域上的投影的范数进行研究.

若F∈Θ(H)，则R(F)闭,且F可以写作如下2×2矩阵形式

(1)

其中F1∈B(R(F)⊥,R(F)),I为R(F)上的单位算子.

2 主要结果

引理1[6]设E∈Θ(H)具有式(1)的形式，I1和I2分别表示子空间R(F)与R(F)⊥上的单位算子,则有

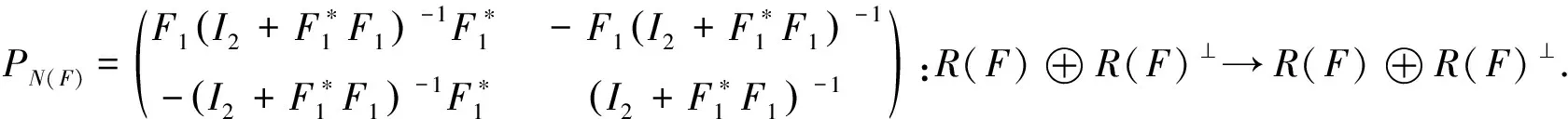
下面的定理1借助算子分块技巧，给出这一结论的等价形式.

定理2 设非零算子F∈Θ(H)，且I-F非零，则：

(1)sup{‖PQPN(Q)‖:Q∈Θ(H)且R(Q)=R(F)}=1同时

inf{‖PQPN(Q)‖:Q∈Θ(H)且R(Q)=R(F)}=0.

(2)sup{‖PQ-PN(Q)‖:Q∈Θ(H)且R(Q)=R(F)}=1.

(3)若dimR(F)<∞或dim(R(I-F))<∞，则

inf{‖PQ-PN(Q)‖:Q∈Θ(H)且R(Q)=R(F)}=1

(4)若dimR(F)=∞且dimR(I-F)=∞，则

inf{‖PQ-PN(Q)‖:Q∈Θ(H)且R(Q)=R(F)}=0

1≥sup{‖PQPN(Q)‖:Q∈Θ(H)且R(Q)=R(F)}

这里选取一秩算子Q1=nx⊗y(n=1,2,3,…)，其中x∈R(F),y∈R(F)⊥都是单位向量,这样就有sup{‖PQPN(Q)‖:Q∈Θ(H)且R(Q)=R(F)}=1.

若取Q=PF，则‖PQPN(Q)‖=‖PF(I-PF)‖=0，也就有

inf{‖PQPN(Q)‖:Q∈H且R(Q)=R(F)}=0.

(2)特别地令Q=PF，则有‖PQ-PN(Q)‖=‖PF-(I-PF)‖=1，因此sup{‖PQ-PN(Q)‖:Q∈Θ(H)且R(Q)=R(F)}=1.

(3)不失一般性，假设dimR(F)=∞,dimR(I-F)<∞，由引理1可知

(2)

因此

inf{‖PQ-PN(Q)‖:Q∈Θ(H)且R(Q)=R(F)}=1.

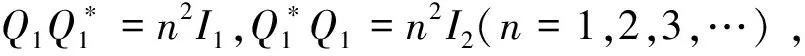
故inf{‖PQ-PN(Q)‖:Q∈Θ(H)且R(Q)=R(F)}=0.