地下快速路驾驶人速度感知敏感性分析及模型构建

张兰芳， 武雅婷， 王淑丽， 史 进

（1.同济大学 道路与交通工程教育部重点实验室，上海 201804；2.上海民航新时代机场设计研究院有限公司，上海 200335）

Analysis and Modeling of Speed Perception Sensitivity of Drivers on Underground Expressways

ZHANGLangfang1，WUYating1，WANGShuli1，SHIJin2
（1.Key Laboratory of Road and Traffic Engineering of the Ministry of Education， Tongji University， Shanghai 201804，China；2.Shanghai Civil Aviation New Era Airport Design and Research Institute Co.， Ltd.， Shanghai 200335，China）

Abstract：To explore the mechanism of the speed perception of the driver， a driving simulation experiment was designed to collect the perceived speed and actual driving speed of the driver， which analyzes the influencing factors such as the geometric alignment of the underground expressway and the side wall change frequency on the speed perception sensitivity of the driver.The prediction model of the speed perception bias sensitivity threshold of the driver was constructed based on the constant speed theory and the machine learning method.The results show that at the 0.05 significant level， there are substantial differences in the speed perception sensitivity threshold of the driver at different speeds ， linear combinations， and sidewall change frequency groups.The Lasso variable filters the characteristic variables according to the short-term， midlong-term， and long-term time windows.The determination coefficientR2of the constructed multivariate nonlinear model is 0.645， the determination coefficientR2of the multilayer perceptron model is 0.727， and the determination coefficientR2of the support vector regression model is 0.853.

Key words：underground expressway； driving simulation； speed perception deviation； sensitivity threshold；support vector regression

为有效解决交通拥堵问题，各城市新建大量城市地下快速路。相比于一般道路，地下道路封闭里程长、环境单调，更易导致驾驶人判断车距和速度的能力减弱［1］。从上海市外滩隧道入口前与隧道中的监控视频中可以看出，隧道内部车辆超速频繁，在夜晚可出现100%的车辆速度达到60 km·h-1的现象，而地面车辆夜晚超过60 km·h-1的只有2.82%。结合外滩隧道事故记录可以发现，大多数严重事故与超速有关。尤其是被动无意识的超速行为，驾驶人不能有效地感知地下道路环境，准确估计驾驶速度，导致车速偏离预期，严重影响运营安全。因此提升驾驶人在地下道路环境中的速度感知能力，对于管控地下道路行车风险具有重要意义。

相关研究表明，速度知觉（speed perception）属于运动知觉，受到空间知觉与时间知觉的影响［1］。速度知觉具有恒常性的基本特征，受外界刺激不断变化且相互干扰，包含较多的信息噪声，但先验知识的存在，让人类产生速度维持不变的心理倾向性，且速度知觉具有阈值性，过快与过慢的运动都不能让人类产生明显的知觉，这与人类感受器的敏锐性有关。在驾驶过程中，驾驶人的速度感知主要包括直接感知与间接感知，直接感知主要通过视觉、听觉、运动3种方式实时感知，数值往往为一个范围，而间接感知是通过查看仪表盘方式，存在时间滞后性，但很精确［2］。

目前针对速度感知的模型构建主要依赖于比例模型与贝叶斯模型。比例模型［3-5］提出速度感知取决于刺激对比，在低速条件下降低对比度会减弱速度感知能力，若时间频率增大，会引起速度高估，且两者存在比例关系。这一学说得到广泛认可［6-7］，但需要将高速与低速分开讨论，分别建立模型。而贝叶斯模型认为人类速度感知是具有偏差性的，并不完全取决于自然环境，人类的主观意识与客观环境共同影响速度感知，且一般的先验速度感知具有较慢的倾向，这与人类生活的环境速度较慢有关，所以被试验者在实验中多低估物体的运动速度［8-9］。比例模型只考虑了客观环境变化，而忽略了测试者的主观特性，而贝叶斯模型无法获得主观认知速度的增大或减小，只能定性分析，不能定量分析。

本文基于八自由度驾驶模拟器，采集驾驶模拟得到的实际行车速度，以及驾驶人主观感知速度，分析地下快速路线形、侧壁变化频率等因素对驾驶人速度感知敏感性的影响，并基于恒定速度理论、机器学习方法构建驾驶人速度感知偏差敏感性阈值预测模型，从而为地下道路景观设计以及运营管理提供参考，并为治理超速行为提供理论依据。

1 地下道路速度感知敏感性影响因素

1.1 速度感知敏感性描述方法

驾驶人在驾驶过程中面对相同景观环境时会产生差异性的感知，进而做出不同的决策与操作，这种现象称为驾驶人速度感知敏感性差异。速度感知敏感性强的驾驶人可以迅速感知到速度变化的细微差异，敏感性差的驾驶人则不能感知出因操作波动导致的速度偏差。同时，驾驶人敏感性存在阈值，只有当速度偏差达到阈值，驾驶人才可以意识到主观认知速度存在偏差，并且阈值越大，驾驶人敏感性越低，因此要采用合理的方法提取速度感知偏差敏感性阈值。

驾驶人速度感知敏感性可以通过主观认知速度与真实行车速度的差值表示，该差值的绝对值越大，驾驶人感知敏感性越低，越容易发生非主观超速行驶行为。速度感知敏感性表达式如下：

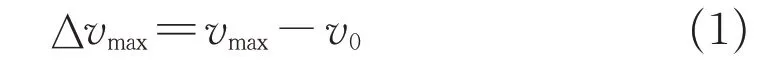
式中：Δvmax为驾驶人意识到速度偏差之前时段内真实速度与主观认知速度的最大速度差；vmax为某一时段车辆最大速度；v0为某一时段主观认知速度。

驾驶人在驾驶过程中会忽视较小的速度偏差，将某一范围内的速度波动视为匀速行驶，因此应剔除驾驶人允许偏差，对Δvmax进行修正，表达式如下：

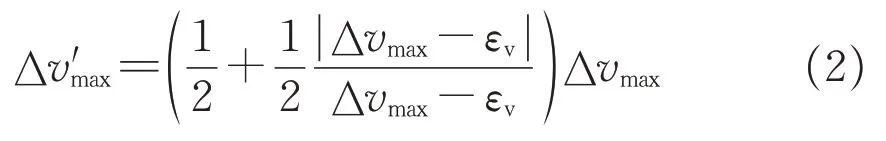
式中：Δv′max为修正后的真实速度与主观认知速度最大偏差；εv为不同驾驶人认为没有差异的速度差，即不同驾驶人认知速度误差允许值，当速度最大偏差小于该值，则不将该差值视为速度感知偏差。

1.2 地下道路速度感知影响因素

速度感知影响因素众多，是物体本身的速度与环境变化的耦合过程。具体到道路交通领域，车辆大小与类型［10-11］、车辆声音［12］、道路景观绿化［13］、光照条件［14］、道路几何线形［15］等都会影响驾驶人的速度感知与判断。针对地下道路环境，探讨下列可能存在的速度感知相关影响因素。

1.2.1 几何线形

道路几何线形指道路在空间中的形状，包括平纵横3个断面。考虑地下道路工程实际情况，根据《城市地下道路工程设计规范》，现存地下道路多采用双车道加应急车道的形式，建筑高度受地形限制多为5 m左右，变化范围较小。同时，本研究主要采用驾驶模拟技术开展，不同纵断面坡度、横断面范围在地下道路封闭环境中辨识度不大，所以道路线形只考虑平面半径，即曲率对于驾驶人速度感知的影响，如表1所示。

表1 道路线形对速度感知的影响Tab.1 Influence of road alignment on speed perception

1.2.2 光照

相关研究表明，速度感知能力受到昼夜光照强度的影响［16-17］。而城市地下道路照明设计由道路设计速度、设计交通量、洞外亮度、气候条件等因素决定［18］，在实际运营中，由于光照设备老化或节约运营成本，洞内光照强度可能存在不满足规范标准的情况，所以将光照强度这一影响因素考虑到速度感知研究中。

1.2.3 侧壁变化频率

当地下道路侧壁采用拼接形式时，驾驶人在车辆行驶过程中，会观察到拼接缝以一定的频率不断后移，当侧壁变化频率较低时，驾驶人会产生速度低估情况，当侧壁变化频率较高时，驾驶人会产生速度高估情况，频率过快时，驾驶人甚至会产生眩晕。所以研究不同侧壁变化频率对驾驶人速度感知的影响具有可行性。

2 驾驶模拟实验及数据处理

2.1 实验场景设计

实验针对40、60、80 km·h-13种不同的主观认知速度设计路线，每个路线分为适应路段和实验路段。适应路段为了让驾驶人在实验开始前感受不同行车速度；实验路段通过设置500、1 000、2 000 m半径圆曲线及直线4种线形单元进行组合，缓和曲线根据规范设置，超高根据设计速度及曲线半径按照规范设置。

关于光照场景设计，在规范中不同交通量、速度条件下的亮度要求取值为1～10 cd·m-2；在驾驶模拟实验中，当场景设置的时间为06：00—12：00，地面亮度取值为1～13 cd·m-2时，可以覆盖地下道路所有光照场景，所以将地下道路场景的光照条件设置为每个路段的光照在06：00—12：00随机变化。

在隧道装饰设置中，本文结合隧道侧壁设置不同长度的素混凝土板，可将板缝作为图案，一共设置长板20 m、中板10 m、短板5 m共3种宽度板型。侧壁板长与频率转化如下式所示：

式中：f为侧壁变化频率；vi为第i个样本的车辆速度；Li为第i个样本的侧壁板长。

综上所述，将3种设计速度路线与3种板长结合，共设计9种实验场景，具体参数设计如表2所示。

表2 地下道路场景设计参数Tab.2 Scene design parameters of underground expressways

2.2 实验人员

本文重点研究地下快速路环境因素导致的驾驶人速度感知偏差，因此在进行实验对象选择时，对驾驶人相关因素进行了控制。实验共招募有隧道行车经历的熟练驾驶人25人，其中男20人，女5人，身体健康，无驾驶模拟眩晕症状，基本信息见表3。

表3 驾驶人基本信息Tab.3 Basic information of drivers

2.3 实验流程

正式实验开始前，参与实验者在模拟器内驾驶3～5 min以熟悉驾驶模拟环境。之后，要求在9组实验场景下按照提示分别保持40、60、80 km·h-1的速度行驶，行驶过程中应多次观察仪表盘以及周围环境，充分感受速度，直至该场景结束。

2.4 数据处理

数据来源主要是驾驶模拟软件导出的车辆行驶数据和驾驶人操作数据。根据拉依达准则，剔除驾驶表现异常的驾驶人数据，剩余20名驾驶人的有效数据，每位驾驶人有9个场景，共计180个完整的原始实验数据样本，从而保证了实验数据的有效性。驾驶模拟数据主要包括车辆速度、车辆加速度、横向偏移、刹车踏板力度、油门开合度、当前道路半径、行驶时间、是否查看仪表盘数据。

对收集到的数据进行降噪处理，并依据驾驶人速度拐点与阈值、加速度特性以及驾驶人查看仪表盘状态，将驾驶人行车数据中速度感知阶段数据进行提取。同时，对速度感知阶段数据进行时窗划分。由于驾驶过程是一个短时记忆不断迭代的过程，相关道路标志牌视认实车实验表明，驾驶人感知行车信息30 s后会大量遗忘［19］，因此长期时窗取30 s；同时根据驾驶人反应时间、道路几何设计常用控制指标［20］等状态，取3 s作为短期时窗，相应地取10 s作为中长期时窗口。

3 不同影响因素条件下驾驶人速度感知敏感性阈值分析

3.1 速度

3种不同主观认知速度组别间速度感知偏差敏感性阈值如表4所示。

表4 不同主观认知速度组下速度感知敏感性阈值比较Tab.4 Threshold comparison of speed perception sensitivities of different subjective cognitive speed groups

由表4可知，在不观察仪表盘条件下，驾驶人的速度感知偏差敏感性阈值与速度组别存在相关关系，当主观认知速度为40 km·h-1与60 km·h-1时，驾驶人的速度感知偏差敏感性阈值无明显差异，当速度进一步增大到80 km·h-1时，驾驶人的速度感知偏差敏感性阈值明显增大，速度偏差敏感性显著降低，无法意识到超速状态。所以速度大小会对驾驶人速度感知有一定的影响。

3.2 线形

平面线形主要包括了单一线形与组合线形，单一线形包括了3种不同半径的圆曲线以及直线，组合线形包括了3种不同半径下曲线连接直线和直线连接曲线。不同线形条件下驾驶人速度感知偏差敏感性阈值统计表以及显著性分析如表5～7所示。

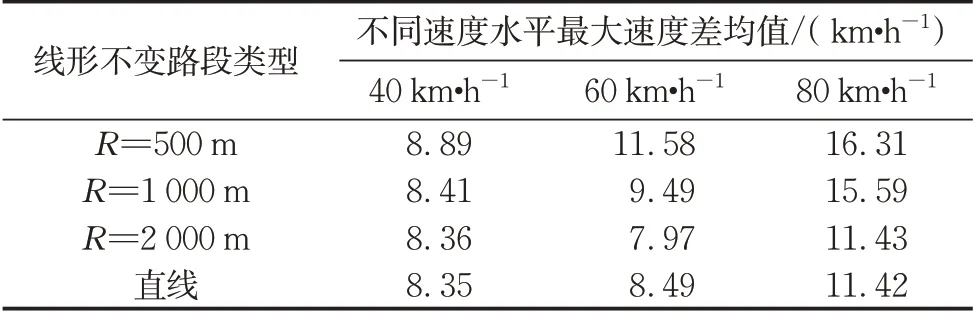
表5 单一线形条件下速度感知敏感性阈值统计Tab.5 Threshold statistics of speed perception sensitivity under single linear condition

由表5～7可知，道路几何线形会对驾驶人的速度感知产生影响，单一道路线形的速度感知能力要好于变化线形的速度感知能力。且单一线形中小半径曲线与大半径曲线的速度感知敏感性阈值有显著差异。当半径逐渐增大，速度水平对于速度感知敏感性的影响逐渐减小。组合线形条件下，直线接圆曲线路段的速度感知能力与圆曲线接直线路段无显著差异；500 m小半径路段接直线组合的速度感知能力要显著小于其他组合。因此路段半径、路段设计速度都会对驾驶人的速度感知产生显著影响。

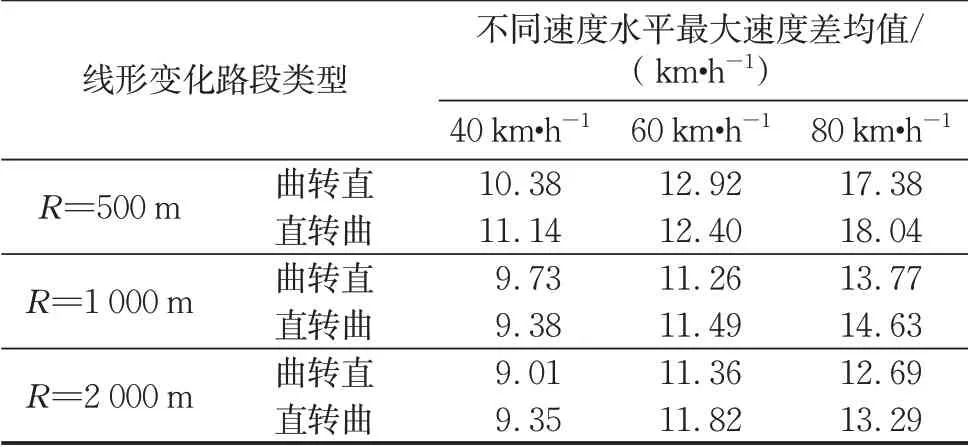
表6 线形组合条件下速度感知敏感性阈值统计Tab.6 Threshold statistics of speed perception sensitivity under linear combination conditions

表7 不同线形条件下速度感知敏感性阈值显著性统计Tab.7 Significance statistics of speed perception sensitivity threshold under different linear conditions

3.3 侧壁变化频率

不同侧壁变化频率下驾驶人速度感知偏差敏感性阈值显著性统计以及不同侧壁变化频率下最大主观认知速度均值如表8和图1所示。

表8 不同侧壁变化频率下阈值显著性统计Tab.8 Threshold significance statistics at different sidewall change frequencies

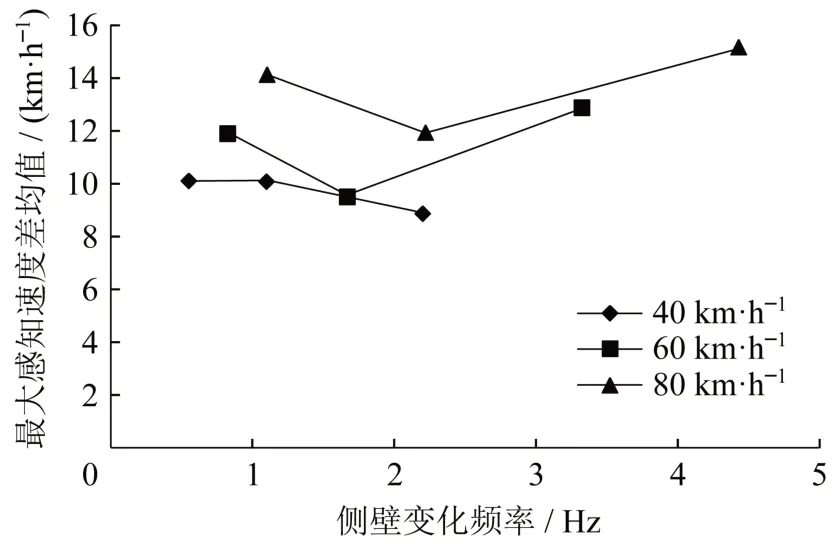
图1 不同侧壁变化频率最大主观认知速度差均值Fig.1 Mean value of maximum subjective cognitive speed difference at different sidewall change frequencies

由表8可得，不同侧壁变化频率以及侧壁变化频率与速度的交互作用会显著影响驾驶人的速度感知能力。同时，由图1可知，驾驶人最大主观认知速度差在侧壁变化频率为2 Hz左右会有较大的下降趋势，这与相关学者给出的合理图案间距是一致的［21-22］。

3.4 光照

本文主要探究地下道路中间路段的驾驶人速度感知与光照的关系。驾驶模拟实验通过改变自然时间，进而改变地下道路的光照条件，故可以用时刻代替不同光照强度。同时，由于亮度与时间近似线性关系，故使用场景中的时间差代替光照强度变化值。根据实验场景设置及片段划分方法，将所有速度感知偏差片段的光照条件分为两种情况，整个速度感知偏差阶段光照强度恒定片段，以及整个阶段光照强度发生变化阶段，并绘制不同光照强度下驾驶人速度感知偏差敏感性阈值以及不同光照变化下最大速度感知偏差分布，如图2、图3所示。

图2 不同光照强度下速度感知偏差敏感性阈值分布Fig.2 Distribution of speed perception deviation sensitivity threshold at different light intensity

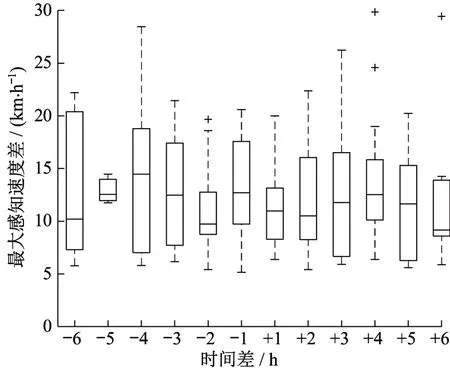
图3 不同光照变化下最大速度感知偏差分布Fig.3 Distribution of maximum speed perception deviation in different illumination changes

由图2、3分析可得，地下道路光照强度以及光照变化与驾驶人速度感知无明显显著相关性。而相关文献中光照强度与速度感知的相关性可能由于白天黑夜光照条件差异过大，环境光照强度已经显著影响驾驶导致［16-17］。而地下道路处于封闭状态，光照强度可以保证驾驶人的通视，即使出于节能考虑或设备老化，也不会出现光照强度过低的情况，所以地下道路的光照强度变化趋势较小，对驾驶人速度感知产生影响不明显。

4 地下道路速度感知偏差敏感性阈值模型构建

4.1 基于恒定速度理论的速度感知偏差敏感性阈值预测模型

驾驶人在行驶过程中，由于惯性意识的存在，主观认知速度随着环境均匀变化，若环境无显著变化，则速度感知保持恒定。实际行车速度主要以主观认知速度为基础，受驾驶人操作波动影响，导致主观认知速度与实际行车速度存在速度差，即速度感知偏差。因此速度感知偏差敏感性阈值由下式表示：

式中：Δvmax为敏感性阈值；vE为环境变化速度；eH为不同环境下驾驶人操作的速度波动。

根据速度感知影响因素分析，周围环境变化主要取决道路线形与侧壁变化频率，因此环境变化速度如下式所示：

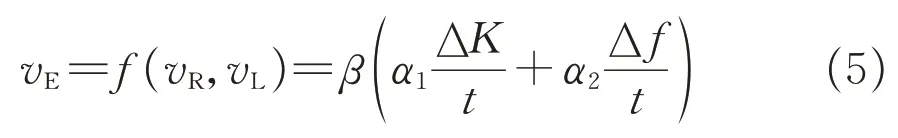
式中：vR为道路线形变化速度；vL为侧壁频率变化速度；ΔK为驾驶人无意识操作时刻的道路线形曲率变化值；Δf为侧壁变化频率变化值；t为行程段的总时长；β为驾驶人环境敏感程度，可采用多维驾驶风格中的谨慎维度分数标准化后代替；α1与α2为常数。

不同环境下驾驶人操作的速度波动如下式所示：

式（6）、（7）中：vp为主观认知速度水平，实验中为规定值，真实环境可用限速值作为近似；R为道路圆曲率半径，用K行程段的平均道路曲率表示；f为侧壁变化频率，具体计算见式（3）；γ为驾驶人操作熟练程度系数，操作越熟练，该系数越小，速度感知偏差越小，可采用驾驶里程S的倒数代替；α3、α4为常数。

对所有自变量进行标准化操作，利用SPSS软件进行非线性拟合，设α1、α2、α3、α4初始值为1，经过迭代后，得到模型如下：

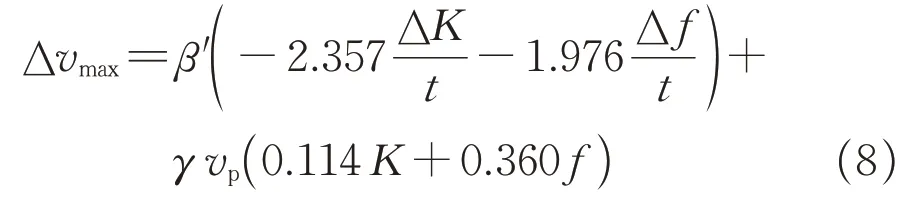
4.2 基于机器学习方法的速度感知偏差敏感性阈值预测模型

4.2.1 压缩系数法变量初筛

从复杂混乱的数据中挑选变量并构建模型，不合理的变量筛选会导致模型拟合效果差、精度降低等，因此需要剔除高度相关自变量，以及与因变量无显著相关性的自变量。本文使用的压缩系数法为LASSO（least absolute shrinkage and selection operator），其前提是“稀疏性假设”，只有有限变量是相关的。

采用上述方法，使得不显著的变量系数压缩为0，以此实现变量筛选，共筛得15个变量，系数值如表9所示。

表9 变量概述Tab.9 Overview of variables

4.2.2 多层感知机人工神经网络

多层感知机（multilayer perceptron， MLP）在模式识别中是经典的监督学习算法，是一种非常常用的拟合复杂函数以及处理分类的手段。将偏差敏感性阈值作为预测变量，变量初筛的15个变量作为自变量并进行标准化处理，样本按照训练集：测试集：验证集=6：2：2划分，通过MLP进行拟合。

4.2.3 支持向量回归

支持向量回归（support vector regression， SVR）具有严格的理论推导，不需要大量训练数据，可以保证全局最优，能够有效解决神经网络的局部最优问题，非线性映射在进行高维度运算时具有明显优势，泛化能力也较其他算法更好。考虑到本研究实验数据样本量较少，变量维数较多，可以采用SVR进行速度感知偏差阈值回归预测。对自变量与因变量标准化后，采用python中SVR函数进行SVR建模。

4.3 建模结果分析

在利用驾驶人速度感知偏差进行预测的时候，共采取了3种方式，基于心理学中恒定速度理论的非线性模型、基于MLP的分类与回归模型、基于SVR的回归模型。回归模型的评价指标主要包括R2决定系数、均方误差（mean squared error， MSE）、平均绝对误差（mean absolute error， MAE）等。

R2决定系数的计算公式如式（9）所示，取值范围为（-∞，1］，若R2接近1表明自变量对因变量的解释能力强，拟合效果好，越小表明拟合效果越差。

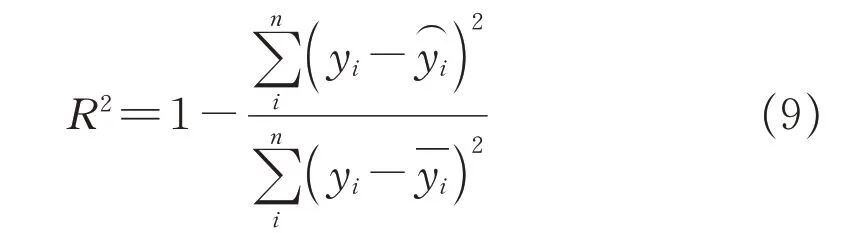
式中：yi为实际值为预测值为平均值。

但R2与数据样本量呈正相关关系，若回归数据样本较大，需采用校正后的R2a进行评价，计算公式如下：

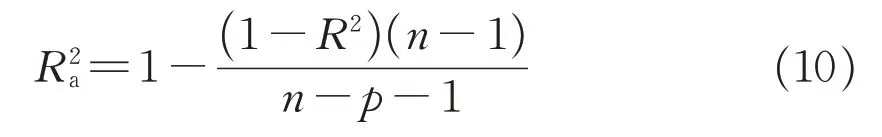
式中：p为自变量数量；n为样本量，可将样本数量与特征变量的数量影响消除。

均方误差计算如下：

平均绝对误差计算如下：

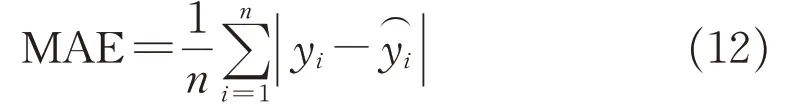
3种模型的评价情况如表10所示。

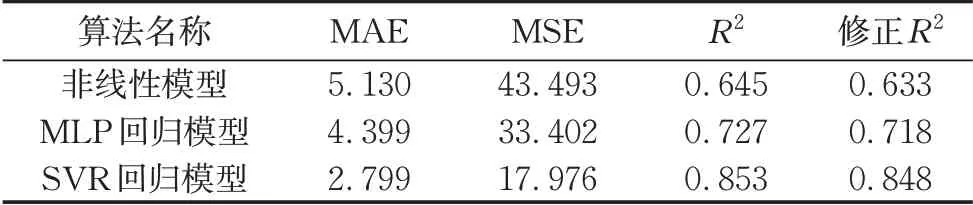
表10 不同模型回归效果Tab.10 Regression effect of different models

从3种模型的回归结构可以看出，SVR模型预测精度最高，但可解释性较弱，非线性模型的精度最低，但具有较强的可解释性，具有一定的物理意义，考虑到是基于人因的预测建模，人行为的不确定性较大，且数据样本量较大，所以R2较小是可以接受的。

5 基于驾驶人速度感知敏感性的地下道路易超速断面识别

根据上文中的地下道路速度感知偏差模型，通过输入整个地下道路的线形、侧壁环境，即可计算出地下道路每一个断面的最大感知速度偏差，绘制地下道路速度感知敏感性热力图，确定速度感知偏差阈值，建立超速风险路段判别标准，具体如图4和表11所示。

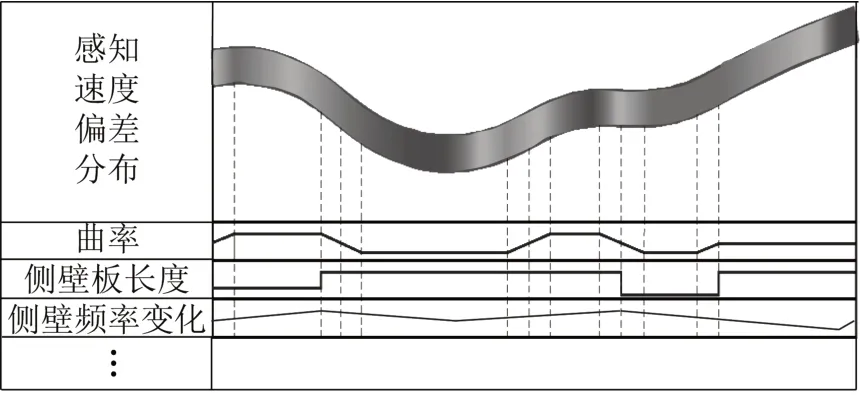
图4 基于感知速度差的地下道路安全设施设置位置示意图Fig.4 Location diagram of underground road safety facilities based on perceived speed difference

表11 地下道路超速风险断面判别标准Tab.11 Identification standard for overspeed risk section of underground road

6 结论

本文基于大型驾驶模拟器实验数据，分析了不同影响因素条件下驾驶人的速度感知敏感性，依据恒定速度原理，构建了基于恒定速度原理的驾驶人速度感知偏差阈值多元非线性预测模型，通过驾驶人谨慎程度、行车曲率变化速率、侧壁板变化频率变化速率、驾驶人驾驶熟练度、道路曲率、侧壁变化频率变量，预测驾驶人速度感知偏差敏感性阈值。使用LASSO对影响因素衍生的不同时窗统计量进行变量筛选，并通过MLP神经网络、SVR支持向量回归算法，预测驾驶人速度感知偏差敏感性阈值，并对3种模型回归效果进行评价。对比可得，机器学习模型拟合效果较优。最后，依据地下道路断面速度感知偏差敏感性阈值是否超过道路限速值的20%、10%，将不同的道路断面划分为超速高风险断面、超速中风险断面、一般断面，可以针对性给出不同的设施优化方法，从而有效诱导车速处于安全范围，降低行车风险。

作者贡献声明：

张兰芳：建立系统架构，论文审阅与修改。

武雅婷：建模方法设计，论文撰写。

王淑丽：实验数据分析。

史 进：实验场景设计。