砂土液化后液-固相变机理的单元试验与模拟

倪雪倩， 叶 斌

（1.中南大学 土木工程学院，湖南 长沙 410018；2.同济大学 土木工程学院，上海 200092）

地震砂土液化是一类重大地质灾害，严重威胁人类生命安全和基础工程安全。震害调查结果表明［1］，大部分工程建筑破坏发生在液化后的大变形流动阶段。因此，充分研究液化后砂土力学行为对掌握液化灾变及评估液化风险具有重要意义。

在单元试验中，学者［2-4］通常将砂土激振至初始液化状态（即第一次到达零有效应力状态［5-6］），然后进行单调不排水试验以研究液化后砂土的力学行为。然而，既有研究［7-9］主要关注中密砂及密砂，对松砂液化后的力学性质研究少有报道，这主要是由于松砂在动力荷载作用下易产生不可控的流动液化，难以获取初始液化状态［10-11］。Ye等［12］基于流动液化的不可控性，提出应力与应变相结合的三轴试验加载方法，易获取松砂的初始液化状态。因此，本文将采用文献［12］提出的应力与应变相结合的加载方法对松砂进行液化后力学行为研究。

学者［2，4，13］通过试验发现，液化后砂土的剪应变先在极小的常剪应力下逐步发展，刚度极小，当到达某一临界剪应变值时，由于砂颗粒重新排列和内部结构重组［14］，剪应力快速发展。Yasuda等［15］指出，液化后砂土的刚度减小至初始刚度的1/1 000，表现出流体材料性质。陈育民等［16-17］基于试验发现，液化后砂土表现出剪切稀化非牛顿流体，其应力应变率关系可用幂律方程进行描述。类似地，Huang等［9］对液化后砂土进行系列三轴试验发现，液化后砂土呈非牛顿流体性质。近年来，周恩全等［18］考虑了有效固结压力和加载速率对液化后土体性质的影响，建立了液化后流动变形过程中率相关性和孔压相关性流体本构模型。Rouholamin 等［4］发现液化后土体的应力应变关系呈两段式发展：第一阶段土体刚度极低，发生明显的流动，呈现流体性质；第二阶段土体刚度逐渐恢复，剪应力与剪应变呈线性增长关系，砂土表现出固相性质。由此可见，液化后全过程是液-固两相演化过程，即由液相性质向固相性质的转化过程。为了更全面描述液化后砂土全过程力学演化过程，Lombardi等［19］将液化后砂土分为三个阶段，并基于试验提出经验分段函数关系。Prime等［20］在数值软件中利用宾汉姆本构关系模拟液化后土体呈现的流体性质，采用弹性模型模拟刚度恢复的固相性质。近年来，越来越多学者采用类似思路研究相变转化过程。综上所述，砂土液化后液-固相转化全过程的力学性质研究及本构模拟尚处于探索阶段，成果相对匮乏，亟需进一步开展深入研究。

因此，本文着重探讨了砂土在液化后的静力加载过程中，伴随着刚度的恢复，逐渐从流态转化为固态的力学行为特性。首先通过应力与应变相结合方法获取松砂的初始液化状态，进而对松砂、中密砂及密砂试样进行液化后力学性质研究。基于试验结果，本文将提出经验模型以统一模拟液化后砂土从液相到固相转化全过程的力学行为。

1 试验概况

1.1 试验材料与试验仪器

本研究试验材料为日本丰浦砂。丰浦砂是国际上广泛使用的标准砂之一，其主要矿物成分为石英，呈半棱角状，粒径范围0.075 ～0.4 mm，基本物理参数如下：平均粒径D50=0.162，不均匀系数Uc=1.50，曲率系数Cc=0.950，最大孔隙比emax=0.970，最小孔隙比emin=0.611。

本研究采用的由上海交通大学和日本诚试工共同研发的多功能动三轴仪，该仪器由压力控制模块、伺服电路控制模块、三轴压力室和数据采集仪4个部分组成，可提供多种加载模式和循环波形，如图1所示。

图1 多功能动三轴试验仪Fig.1 Advanced cyclic triaxial apparatus

1.2 试样制备及试验过程

本研究采用湿捣法进行试样制备，试样尺寸为直径50 mm，高度100 mm。首先按照目标密度称取一定质量的烘干砂，接着加入5%的脱气水，搅拌均匀并密封放置数分钟，保证砂土颗粒与水充分混合均匀。然后，将湿砂分成5等份。制样前，先在模具底部铺一张直径为50 mm的滤纸，利用勺子将砂逐层加入试样模具内，利用平底捣棒逐层击实至目标密度。为了减小分层效应，在每一砂层表面轻轻刮毛，使当前层与下一层试样充分接触。最后，在制备完成的试样上部放置一片湿润滤纸。

连接试样与加压系统，并施加30 kPa的围压以保证试样稳定性。为了使试样达到完全饱和状态（Skempton B值≥0.98），饱和过程分为三步。首先，利用CO2替换试样孔隙中的空气，然后，通入脱气水以置换试样中的CO2，最后进行反压饱和（背压为200 kPa），以溶解试样内部残留的CO2。完成以上三个步骤后，所有试样的Skempton B值均大于0.98。对饱和试样进行平均有效应力为150 kPa的等向固结试验，然后施加正弦波进行动力加载，频率为0.05 Hz。对于松砂，本研究采用作者提出的应力与应变（-0.05%·min-1）相结合加载方式，以获取初始液化状态，具体操作过程可见文献［12］。对于中密砂和密砂，通过循环加载可直接获取初始液化状态。当试样到达初始液化状态，施加1%·min-1的速率进行不排水单调加载试验以研究液化后土体流态化性质。本文共设置5种相对密实度的饱和砂土，Dr分别为30%、40%、50%、60%和70%。

2 砂土液化后试验结果与分析

2.1 液化后力学响应

图2为松砂（Dr=30%）在不排水条件下的动力响应，循环荷载为32 kPa。由图2可知，松砂在应力与应变相结合加载模式下，有效应力逐步下降，应变和孔压逐步发展，最终发生流动液化。关于液化后力学响应，由孔压时程曲线可知，在轴向应变εa持续作用下，超孔隙水压力保持在1.0 kPa，偏应力q保持在3.0 kPa左右，此时砂土刚度极低，呈现典型流体状态。随着应变的发展，砂土颗粒重新排列，结构发生重组，超孔隙水压力逐渐降低，有效应力逐渐增大，偏应力随应变的增大而增长。应力应变关系表明，试样在重获刚度过程中，偏应力首先缓慢增长，随后增长速度加快，最后偏应力与轴向应变呈线性增长。

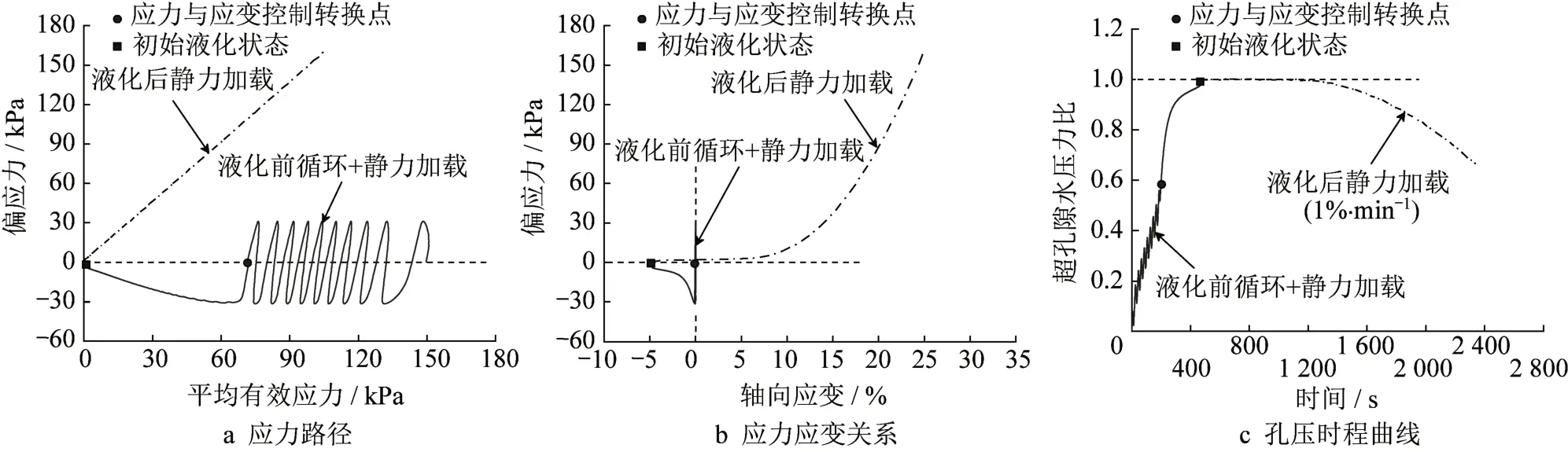
图2 松砂液化后力学响应（Dr=30%）Fig.2 Cyclic behavior of post-liquefied loose sand (Dr=30%)

图3为中密砂（Dr=40%）力学响应特征，实线代表砂土在循环强度为60 kPa作用下的动力响应，点划线表示液化后力学行为。研究表明［21］，液化前的循环强度和频率对液化后砂土的力学性质作用不明显，因此中密砂与松砂的液化触发强度对液化后性质无影响。对比图2和图3，尽管松砂和中密砂的液化模式不同，但是其液化后力学行为特征类似。中密砂在不排水静力加载条件下，超孔隙水压力维持在高水平，偏应力保持在2.0 kPa，砂土呈流动状态。随着应变的发展，液化后的土体结构发生重组，超孔隙水压力逐渐降低，有效应力逐渐增大，偏应力随应变的增大先缓慢增大，之后二者呈线性发展。与松砂不同的是，中密砂发生流动的应变范围较小，土体更快重获刚度。

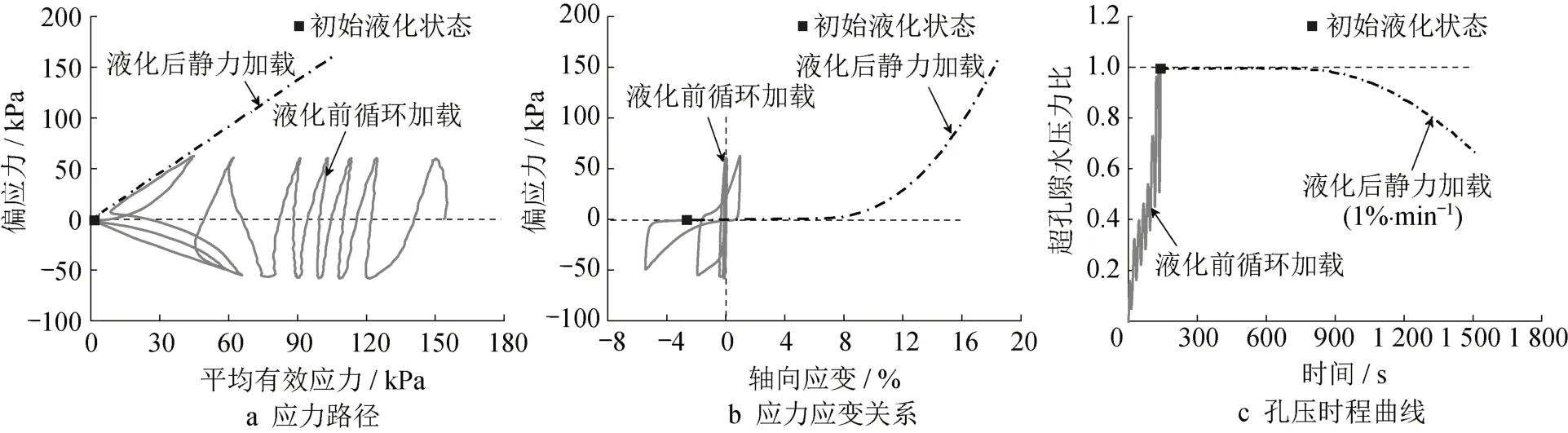
图3 中密砂液化后力学响应（Dr=40%）Fig.3 Cyclic behavior of post-liquefied medium-dense sand (Dr=40%)

2.2 试验结果分析

为了对比分析液化后饱和砂土的力学行为规律，将不同相对密度砂土的应力应变关系进行重新整理。其中，轴向应变转换为剪切应变γ，即

式中：ν为泊松比，在不排水条件下，ν取0.5。

如图4所示，对于不同密度的饱和砂土，偏应力随剪切应变的发展均呈三个不同阶段。首先，土体在较小的常偏应力值下，剪切应变线性发展，应力应变关系呈近似水平直线分布；接着，偏应力随剪切应变的增大逐渐增大，二者呈下凹发展趋势，土体剪切模量逐渐增大；最后，当应变发展到一定程度时，偏应力与剪切应变呈线性增长，即二者的剪切模量为常数。可以发现，在第三阶段，饱和砂土重新获得新的强度，呈现出固体性质。相应地，如图5所示，在饱和土体呈流态化的第一阶段，土体内部的超孔隙水压力保持在最大值，随着剪应变的逐渐发展，内部超孔隙水压力逐渐降低，土体刚度逐渐恢复。当偏应力与应变呈线性增长时，超孔隙水压力比随轴向应变的增大而降低，二者近似呈线性关系。

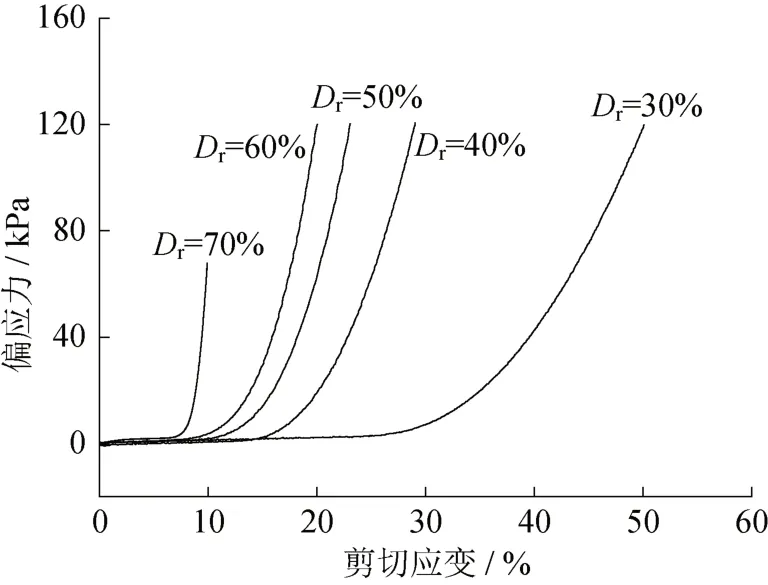
图4 不同相对密度下偏应力与剪切应变关系Fig.4 Deviatory stress versus shear strain at different relative densities

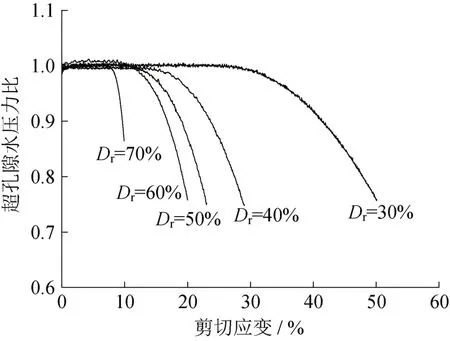
图5 不同相对密度下超孔隙水压力比与剪切应变关系Fig.5 Excess pore water pressure ratio versus shear strain at different relative densities

为研究液化后土体液-固相变转化过程力学性质，本研究将液化后应力应变关系分为三个阶段，如图6和图7所示。第一阶段，液化土体有效应力为零，砂颗粒呈悬浮状态，粒间接触少，因此土体强度低。此时土颗粒整体定向排列，以剪缩为主，剪胀不明显。根据Rouholamin等［4］建议，液化后呈流态化砂土（即第一段阶段）的剪切模量Gf定义为偏应力为1 kPa时对应的应力状态与原点连线的斜率，即

对于第三阶段，由于土颗粒重新排列，颗粒间配位数（即某一砂土颗粒与周围砂颗粒相互接触的数目）较高（图7），內摩擦力较大，应力应变表现出明显的剪胀现象，此时砂土呈现典型的固体性质，取其剪切模量为Gs，如图6所示。此时。对于第二阶段，土体颗粒由完全悬浮状态进行重新排列，土体逐渐由剪缩变为剪胀，颗粒间的配位数逐渐增多（图7），接触力逐渐增大，砂土重获部分强度，因此第二阶段是液-固相性质转化过程。其中，液-固相转化起始点为偏应力大于第一阶段常应力值时对应的剪切应变值γfluid，终点为应力恰好偏离第三阶段线性应力应变关系延长线上的应力状态，对应的剪切应变值γsolid，如图6所示。

图6 液化后砂土液-固相变阶段划分Fig.6 Solid-fluid phase transition stages of post-liquefied sand

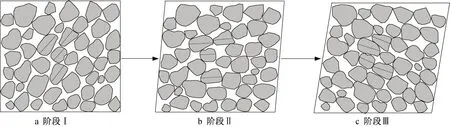
图7 液化后砂土颗粒排列示意图Fig.7 Schematic diagram of sand particles in post liquefaction

图8为不同相对密度下，液化后砂土液-固相转换起始点处剪切应变γfluid和固相起始点或第二阶段终点状态对应的剪切应变γsolid的演化规律。可见，二者的发展趋势类似，随相对密度的增大，γfluid和γsolid均逐渐降低，这意味着相对密度更高的土体呈流态化流动的过程更短暂，刚度恢复更迅速。

γfluid和γsolid与相对密度Dr呈幂函数关系，如图8a所示。

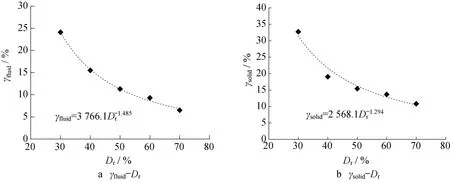
图8 相变点的剪切应变与相对密度关系Fig 8 Shear strain in phase transition state versus relative density

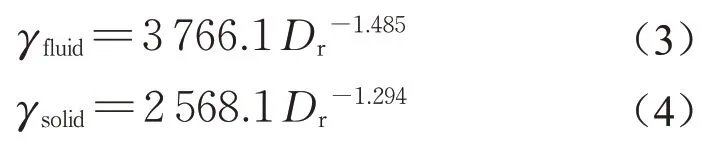
剪切模量是描述土体强度参数之一。对于饱和土体的初始剪切模量G0（循环加载之前），可取土体产生小应变时对应的剪切模量。本文采用Rouholamin等［4］的建议，将第一循环应力应变关系对应的剪切模量视为土体的G0，如图9所示，应力应变的斜率即为G0。液化后土体呈流态阶段的剪切模量Gf可根据式（2）求得。第三阶段固相性质Gs可根据图6获得。

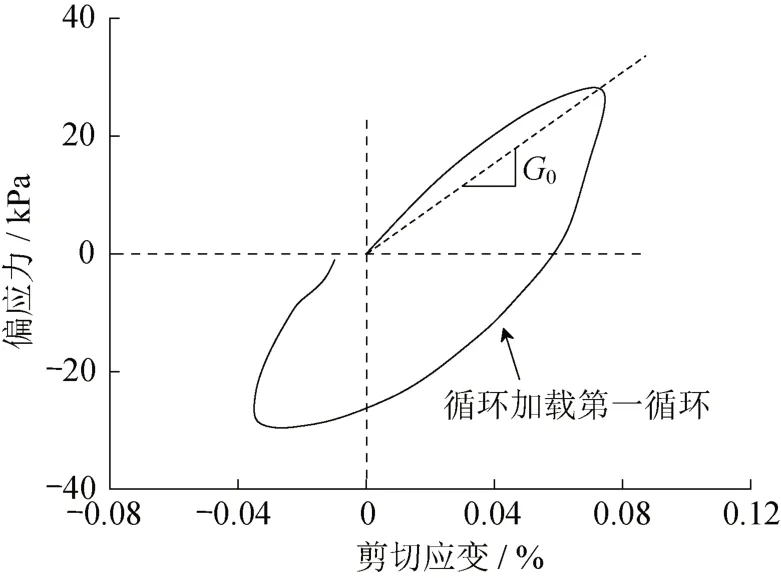
图9 初始剪切模量G0计算方法Fig.9 Measurement of initial shear modulus G0

图10为不同相对密度条件下土体的初始剪切模量G0、流态化阶段模量Gf和固态化阶段模量Gs。整体上，各阶段的剪切模量均随相对密度的增大而增大。其中，初始剪切模量最大，土体在流态化阶段的剪切模量急剧降低，只有初始模量的1/1 000，在较松散状态甚至低于10 kPa。随着应变的发展，土体重获抗剪强度，Gs明显大于Gf，但仍低于初始模量G0。这表明虽然液化后砂土最后重获强度，但短期内土体强度仍无法恢复到初始水平。根据图10可知，G0、Gf和Gs与相对密度呈指数函数关系，如式（5）、（6）和（7）所示。

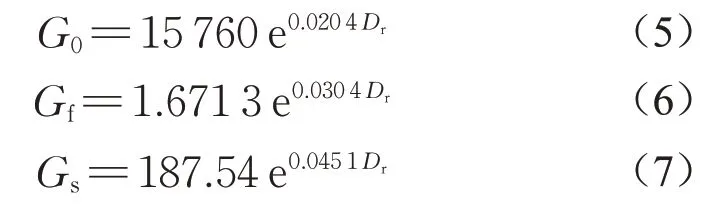
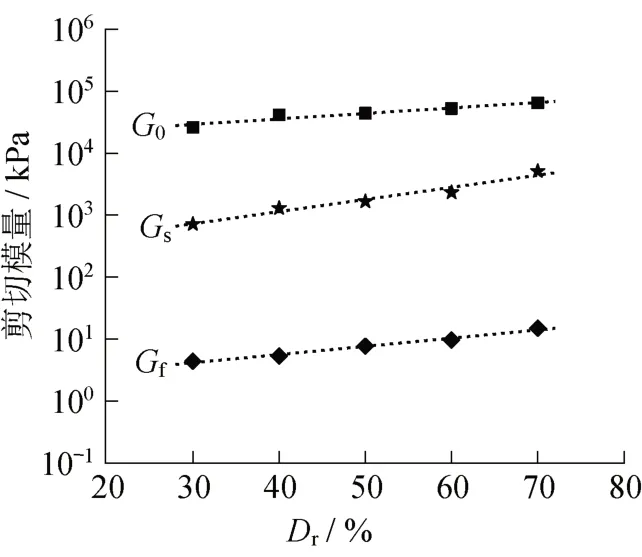
图10 剪切模量与相对密度的关系Fig.10 Shear modulus versus relative density

基于图10剪切模量大小关系，图11给出饱和砂土从受动载初期至最终沉积过程中剪切模量变化示意图。其中，从受震起始状态至初始液化状态，土体受到动力荷载作用，剪切模量呈波动变化不在本文研究范围内，因此用虚线假设其演化规律。液化后砂土呈流态化阶段，土体的剪切模量Gf保持不变。液化后呈固体性质阶段的剪切模量为常量Gs，而从液相向固相转化的过程中，其剪切模量从Gf逐渐增大到Gs。

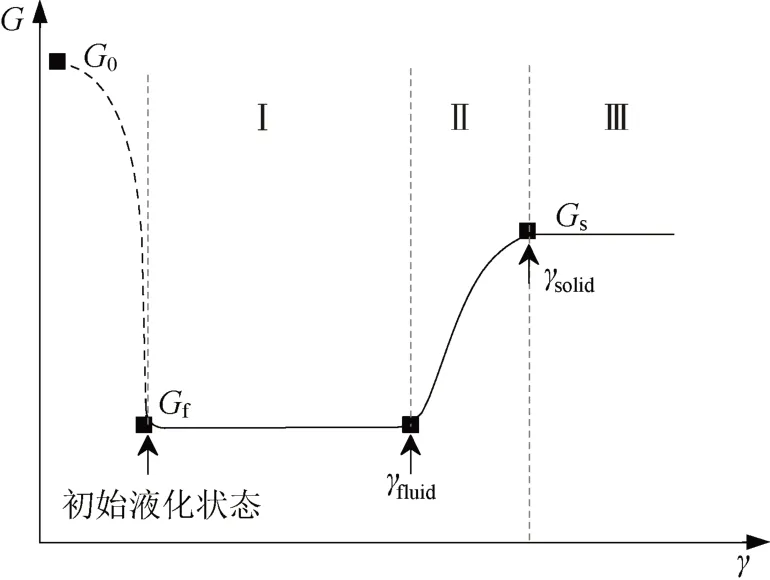
图11 液化后砂土剪切模量示意图Fig.11 Schematic diagram of sand shear modulus in post liquefaction

3 砂土液化后的液-固相变机理的模拟

基于图11所示的饱和土体在液化后三个阶段的刚度变化趋势，本文提出液-固相过渡参数ω以统一描述液化后砂土全过程力学行为。首先，假设土体总剪切模量Gtotal等于液相阶段的剪切刚度Gf和固相阶段的剪切模量Gs的耦合值，在液相阶段，仅Gf起到作用，在固相阶段，仅Gs起作用，液-固相变过程二者共同起作用，因此，总剪切模量表示如下：

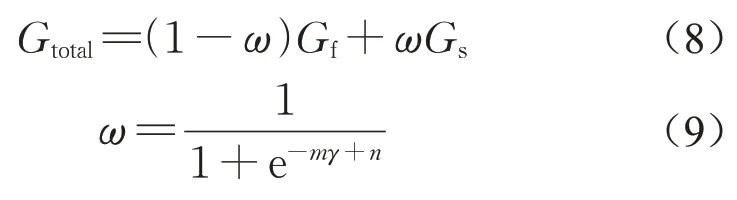
式中：参数m和n决定ω发展趋势。

液-固相过渡参数变化趋势如图12 所示。

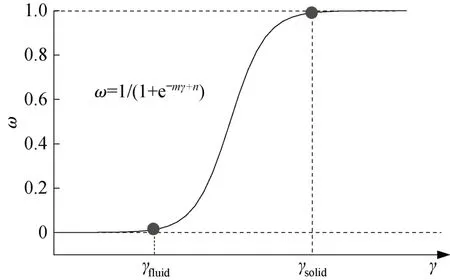
图12 液-固相过渡参数变化趋势Fig.12 Evolution trend of fluid-solid phase transition parameter

当剪切应变小于γfluid时，液化后土体呈现流体性质，过渡参数ω为0，此时总剪切模量均由Gf承担，Gs无贡献。当土体进入强度恢复阶段，即液相向固相过渡阶段，ω介于0和1之间，此时Gf和Gs共同起作用。当剪切应变大于γsolid时，即土体的应力应变关系呈线性发展时，过渡参数等于1，此时Gf不起作用，只有Gs起作用。根据刚度的统一描述，从而实现液化后砂土三阶段力学行为的统一描述。

为了获取应力应变关系，将土体的剪切模量进行剪切应变积分，即

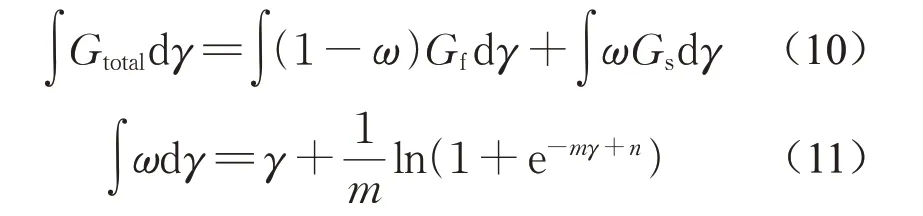
因此，可以得到

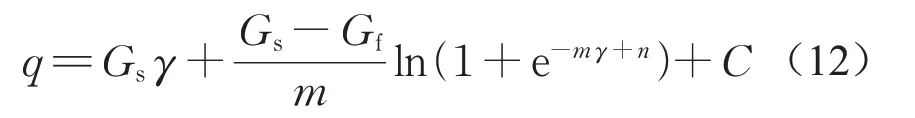
公式（8）～（12）是基于试验结果提出的本构模拟方法。在实际应用中，可根据以下步骤进行模拟：

（1）已知相对密度Dr，根据式（3）求得γfluid，根据式（4）求得γsolid。

（2）根据式（6）求出Gf，根据式（7）求出Gs。

（3）由γfluid和γsolid确定m和n的值。

（4）计算C值。

（5）根据式（12）进行液化后力学行为的模拟。

图13为上述统一本构模型模拟的液化后砂土液-固相变全过程结果。与图4的试验结果相比较，可以看出，液-固相变转化模型能很好地描述饱和砂土液化后的力学行为。

图13 不同相对密度下液-固相变全过程模型模拟结果Fig.13 Simulation result of fluid-solid phase transition model

4 结论

本研究针对丰浦砂开展了一系列不排水加载试验，研究了液化后砂土的不排水力学行为及其本构模型。主要结论如下：

（1）液化后砂土的应力应变关系呈三阶段发展：首先在极小的常偏应力值下，轴向应变不断发展，应力应变关系呈近似水平直线分布，土体呈流体性质；接着，偏应力随应变的增大逐渐增大，二者的关系呈下凹趋势发展，土体的强度逐渐增大，土体呈固、液共存状态；最后，偏应力随应变呈线性增长，此时土体剪切模量为常数，土体呈固体性质。

（2）第一、二阶段的应变分界点γfluid和第二、三阶段应变分界点γsolid均与相对密度呈幂函数关系。

（3）饱和土体受荷载初期的剪切模量G0、流态化阶段剪切模量Gf和固态化阶段剪切模量Gs均随相对密度的增大而增大。G0、Gf和Gs分别与相对密度呈指数函数关系。其中，呈现流态化的土体剪切模量Gf最小，初始剪切模量G0最大，呈现固态性质阶段的土体剪切模量Gs介于二者之间。这表明液化后再次沉积土体强度在短时间内仍低于初始状态。

（4）基于试验结果，引入液相与固相的相变转化参数，建立液化后土体的应力应变关系，统一描述砂土呈现的流体性质和固体性质。模拟结果表明，本文提出的模型能较好地模拟液化后饱和砂土从液相性质到固相性质的力学行为。

作者贡献声明：

倪雪倩：试验分析及论文撰写。

叶 斌：研究思路指导及论文订正。