基于三方博弈的城市更新公私合作项目风险分担模型

杜学美， 李美菱， 黄玉洁， 唐 星

（同济大学 经济与管理学院，上海 200092）

城市衰退已是城市发展过程中不可避免的问题，城市更新将会是改变城市衰落面貌的重要途径。将PPP（public-private partnership，即政府和社会资本合作）模式应用于城市更新建设领域能够有效缓解政府财政负担并实现多方共赢。但是PPP模式下城市更新项目具有投资大、建设周期长、利益主体众多且关系复杂等特征，带来了融资风险大、风险分担不均、利益分配不均等问题。因此，研究城市更新PPP项目的风险分担具有重要意义。

许多学者对PPP项目风险分担的原则和机制进行了研究。Vega［1］通 过分析BOT（build-operatetransfer）项目的建设运营情况，认为风险分担方案应当建立在各方共识的基础上，其分担原则为整体控制力最强和风险控制成本最低；Frederick［2］认为，风险分担应当依循风险管理总成本最小的原则；吴孝灵等［3］借助前景理论构建了PPP项目中私人投资者在政府补偿情境下的投资决策模型，数据分析的结论表明私人的最优投资及其规避程度取决于政府事前的不同补偿契约参数；Wang等［4］引入互惠偏好理论分析了最适合政府的风险分担比例，并在此基础上建立保障项目收益的最优激励机制；王莲乔等［5］通过实证研究了PPP项目的财务风险与融资强度的关系，以及私营部门投资比例和国家宏观环境对这一关系的联合调节效应；Ling等［6］分析出PPP模式中实现市场需求变化风险分担的主要方式是确定最低需求保障，在此基础上进行案例研究，提出在项目合同中应明确规定风险和风险范围、具体实现方式等管理启示；汪勇杰等［7］引入长期合作机制，利用演化博弈理论构建了公共文化PPP项目的风险分担演化博弈模型，分别讨论了公共部门与私人部门在长、短期合作时的合理分担比例，并研究私人部门的行为决策和分担风险意愿，以促进公私部门在公共文化PPP项目中更好地合作；李壮阔等［8］引入激励、惩罚、补偿系数，基于演化博弈理论建立模型，并将公众方纳入模型中分析各参与方的稳定均衡策略，并提出了设立公众投诉举报体系等有助于PPP项目三方建立可持续性合作关系的建议；Carbonara等［9］提供了一种可以实现公私双方共赢、风险共担的最优特许权期决策模型，考虑到PPP项目的不确定性，采用蒙特卡洛模拟了意大利BOT港口项目，验证了模型的适用性；高静［10］识别与归类了公路PPP项目的风险因素，建立共担风险的修正Shapley值模型，增加了风险分担结果的客观性与合理性；周正祥等［11］从政府和社会资本的角度出发，分析了经济新常态下我国运用PPP模式的现状以及存在的问题，并提出了要加强识别PPP项目融资风险和制定风险机制等政策建议。

PPP模式在港口项目、水利工程等领域的应用已经较为广泛，但是其在城市更新领域的应用刚刚兴起，目前相关的研究主要集中于对该模式的可行性分析和运行建议。例如，喻燕［12］基于我国的政治经济环境以及典型实践案例对我国“城中村”改造项目引入PPP模式进行了可行性分析和全面的应用设计，并提出了一些推进该模式市场化运作的建议；徐振强［13］借鉴英国城市更新推行PPP模式的经验，对我国推行PPP模式的潜在问题进行了分析并提供了可参考的发展思路。该领域风险方面的研究多集中于PPP模式下城市更新项目的风险因素及控制对策。李倩倩［14］采取问卷调查的方式，分析廉租房PPP项目关键风险因素，并制定了风险分担机制，设计了服务定价结构和特许经营期限；王东东［15］针对PPP模式下西安“城中村”改造项目进行风险识别和评价，利用风险分担效用，建立公私双方之间在承担意愿和项目收益之间的博弈，得到了纳什均衡解，获得了使项目总效益最大化的风险分担比例和利益分配比例；许豪［16］识别出“城中村”改造PPP项目中的风险因素，采用OWA（ordered weighted averaging）-灰色聚类评价法构建风险评价模型，并以西安市高新区鱼化寨改造项目为例进行了实证研究；任志华［17］对“城中村”改造PPP项目的风险管理主体责任进行划分，构建出该项目的风险分担框架，有利于实现风险的分配、管理与化解；范新华［18］基于风险分担的原则，将识别出的各个风险从理论上在政府部门与私营部门间进行了合理的分配。

纵观上述文献，城市更新这类大型项目中关于具体PPP模式下风险分担可参考的模型极少。一方面，风险分担机制主要以“理性人”为假设，忽略了项目参与方的风险偏好以及风险因素的不确定性，并且对共担风险仅停留在定性描述，很少定量地确定各方的风险承担量；另一方面，私营部门内部也存在着风险和收益的博弈，然而，目前关于PPP项目风险分担的研究多聚焦于政府部门和私营部门之间的风险分担，而少有研究考虑到私营部门内部的风险分担情况。实际中，由于城市更新项目具有投资大、专业性强等特点，其涉及的私营部门既应具备极大的投资金额储备，也应具有运营项目的专业能力，相对应的投资公司和专业运营公司也会存在风险和收益分配的博弈。因此，区别于以往仅考虑政府和私营部门风险分担的类似研究，本文将考虑政府、专业运营公司和投资公司3个参与方的PPP城市更新项目风险分担，同时考虑了不同参与方的风险偏好，并将项目风险量化为风险溢价，使得风险在政府部门和私营部门之间合理转移的同时，也实现风险在私营部门内部的合理分配。

由于随机合作博弈理论常用于解决参与方达成合作时分配合作收益和风险的问题，且城市更新这类大型项目的风险具备较强的不确定性，因此本文运用随机合作博弈理论，充分考虑了政府部门、专业运营公司和投资公司3个参与方的风险偏好、合作关系以及不确定下的随机合作特征，结合Shapley值法，建立基于随机合作博弈理论的城市更新PPP项目风险分担比例决策模型。期望通过三方的风险转移和风险分担，保证项目风险在政府和私营部门之间合理分担的同时，也可以在私营部门内部得到合理分配，从而最大程度降低总风险。同时，对风险分担的研究不仅停留在定性分析，而且能够借助最优风险分担比例模型，量化各自承担的风险量，确定3个参与方应当承担风险的具体比例和相应的风险收益。本文的研究旨在使公共部门和私营部门以及私营部门内部均达到最优风险分担，进而提高各参与方主动参与项目的积极性，为PPP模式多方利益分配决策提供依据。

1 基于随机合作博弈的风险分担比例模型构建

1.1 随机合作博弈理论

合作博弈理论最早于1988年由Edgeworth在他的《数学心理学》中提出，通过在博弈者之间设定有约束力的协议组成联盟，彼此合作以谋求更大的总支付。合作博弈的基本前提：一是集体理性，即联盟的整体收益大于每个成员单独经营时的收益之和；二是个体理性，即联盟内存在帕累托改进性质的分配规则，每个成员所得收益大于其各自为政时所得。传统合作博弈将联盟收益看作确定收益，但在PPP模式下城市更新项目中风险因素的不确定性，可能造成该项目收益的随机性。随机合作博弈满足标准合作博弈模型的个体理性和集体理性，突破了确定联盟收益的限制，更适合不确定性问题的解决［19］。

假设一个随机博弈合作博弈由元祖Γ=(N，{R(S)}S⊂ϑ，{≿i}i∈N)表示，其中N为随机合作博弈的成员，R(S)代表合作联盟的非负随机收益，ϑ为非0随机收益联盟的集合，{≿i}为PPP模式下城市更新项目参与者i的偏好关系集。这样PPP模式下城市更新项目参与者的收益分配可以用(X1，X2，…，Xn)来表示，且PPP模式下城市更新项目参与者i的收益为Xi，Xi=di+ri(R(S)-E(R(S)))，其中第一部分di是对期望收益E(R(S))的分配，第二部分是对残值的分配，也可以看作PPP模式下城市更新项目参与者随机收益R(S)的风险。

1.2 PPP模式下城市更新项目风险分担的随机Shapley值

PPP模式下城市更新利益主体的风险态度水平将决定其风险行为，从信息经济学角度，参与各方风险态度水平可分为风险激进型、风险中立型和风险规避型。风险共担的情况下，项目参与各方的风险水平是可控制的，因为政府参与方与私营部门对其都是风险规避的，差异在于双方规避的程度上，其效用函数ui=e-rix，ri＞0为参与者i的绝对风险规避系数，ri越大说明越厌恶风险。

在假定参与各方风险偏好条件下，参与各方还应该满足Shapley值。Shapley值是根据联盟中成员的贡献程度来分配利益以提高成员积极性，既满足个体理性又满足集体理性的唯一存在解，其原理和结果被各个合作方视为公平，结果易于被各方接受。此外，还可以根据不同领域的特点对Shapley值进行调整和修正，从而得到更加符合实际、更准确的结果。因此，在风险收益成为随机变量的情况下，首先应该设定PPP模式下城市更新项目随机合作博弈的Shapley值模型。

假设一个合作博弈(N，v)，V(∅)=0且V(S)是联盟S的随机收益。Π(N)是所有字典排序β：[1，2，…，n]→N的集合。Sβi={β1，β2，…，βi}为字典排序β的前i个成员的集合，且Sβ0=∅。成员i对联盟Sβi的边际贡献为

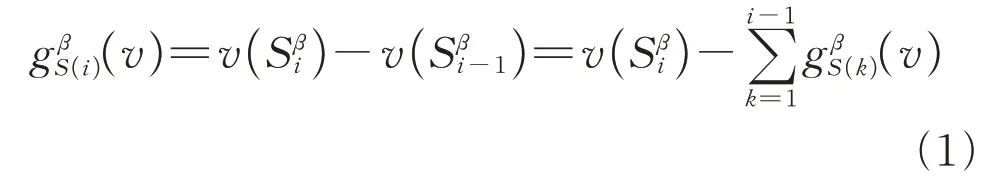
对于任意i=1，2，…，n，Shapley值φ(v)等于边际贡献的平均值，即

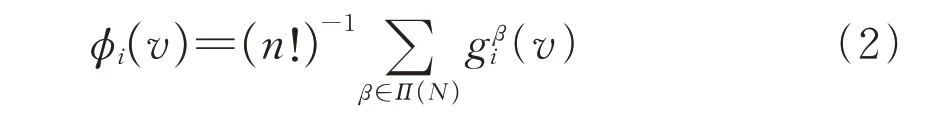
假设成员i具有冯·纽曼-摩根斯坦偏好，令其中E(Ui(R))表示期望效用。若转换函数αi(X，Y)可以使得成员i认为X无异于Y，则αi(X，Y)=E(Ui(R(S)))/E(Ui(R(T)))。 Suijs等［20］证明了在随机合作博弈中，对于每个成员i，存在一个确定性等价gi无差异于他的随机收益。用确定性等价来代替期望效用，得到

于是，构建PPP模式下城市更新项目参与各方的Shapley值为

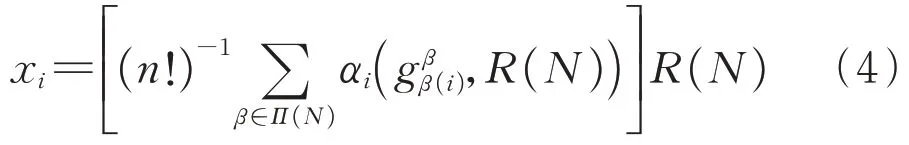
式中：β∈Π(N)是联盟N的一种字典排列，该字典排列下成员i的边际贡献为

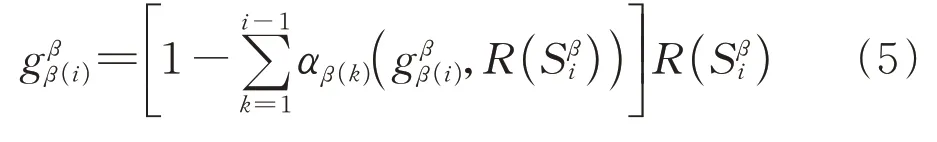
由于PPP模式下城市更新项目主要涉及到政府公共部门及私营部门开发方，其中私营部门是由专业运营公司和投资公司组成的联盟S，根据随机合作博弈理论，各参与方的风险分配比例p={p1，p2，…，pn}，且满足∑pi=1，则称该分配有效。由于城市更新项目的周期长、投资金额大，因此公共部门和私营部门的共担风险主要依靠参与主体的风险厌恶程度和承担意愿来合理分担风险，这样才能保证项目长期处于掌控范围内，促进稳定的合作和参与方的利益追求。考虑到公共部门和私营部门的风险偏好和谈判能力不同，参与主体的风险分担比例是不同的，对应的Shapley值中的权重是不同的，所以用风险分担比例p1、pS代表Shapley值中的平均权重(n！)-1，其中p1+pS=1，则两个部门的Shapley值为

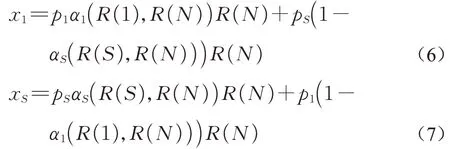
将专业运营公司和投资公司分别看作是参与者2和参与者3，对于整个PPP项目而言，pS2和pS3分别为参与者2、3的风险分配比例，且p*S=pS2+pS3，pS2=p*Sp2，pS3=p*Sp3。其中p2、p3分别是专业运营公司和投资公司在联盟S内承担的风险比例，用p2、p3代表平均权重(n！)-1，p2+p3=1，则联盟S内部专业运营公司和投资公司的Shapley值为

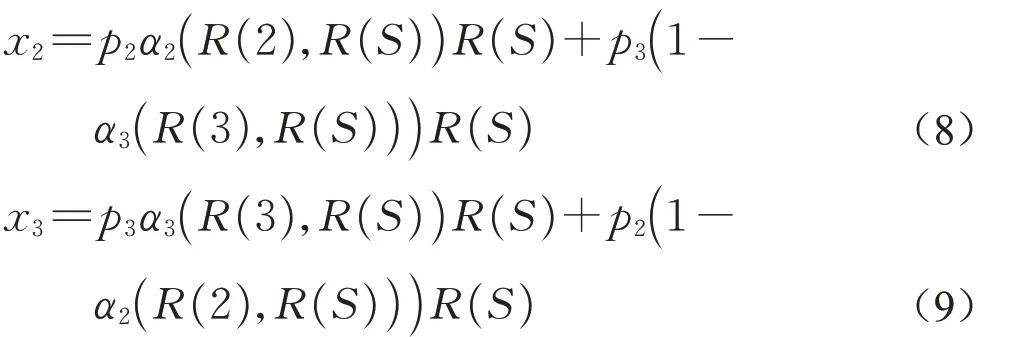
1.3 基于随机合作博弈的最优风险分担模型

PPP模式下城市更新项目能否投资建成的关键取决于包括公私合作是否能够资源互补、能力互补，以促使PPP项目投资效益的风险最小化而收益最大化。所以，合理化的参与和合作是该博弈下的均衡策略，获取项目参与的最优权重p值，能够促成合作的收益的最大化，此时

对于PPP模式下整个城市更新项目而言，收益的期望值为：E(x1)+E(xS)=E(R(N))，说明项目的期望收益为相对固定值。从而可以将求项目收益最大化转化为求风险溢价最小，建立最优化模型如下：

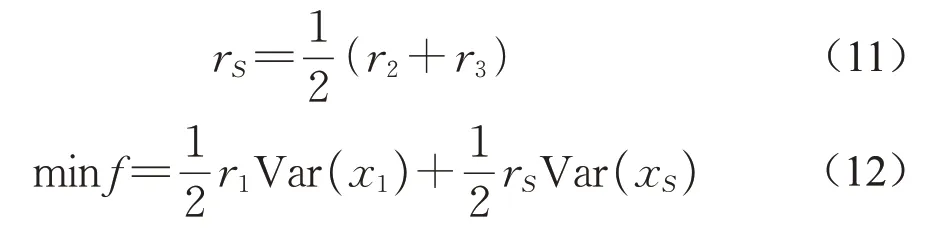
同理可以得出私营部门联盟S内的风险分担模型如下：

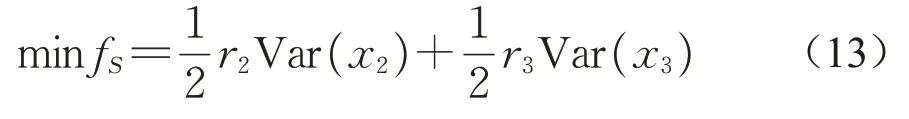
2 模型求解

针对项目整体的优化模型建立拉格朗日方程：

根据方程获得PPP模式下整个城市更新项目的风险溢价对概率的一阶最优条件为

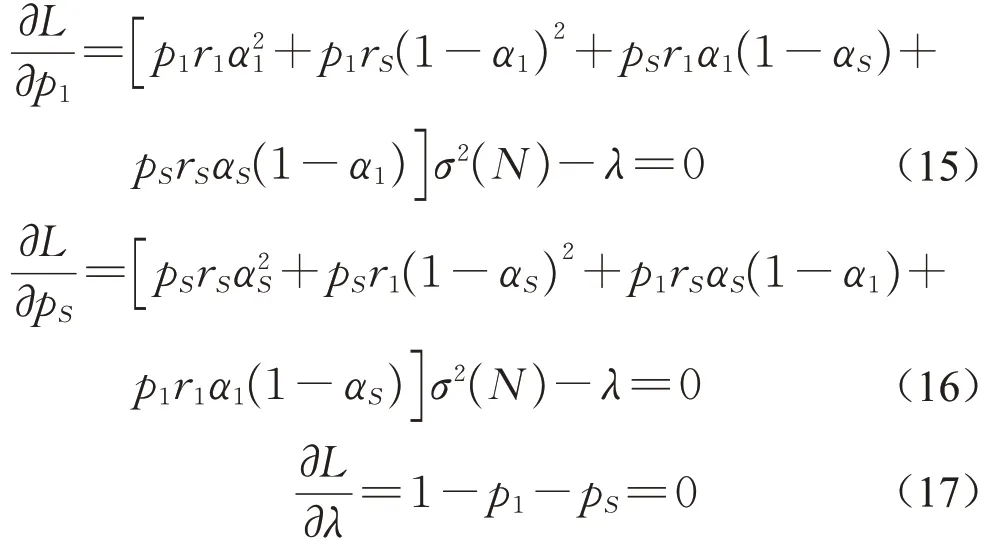
其中，

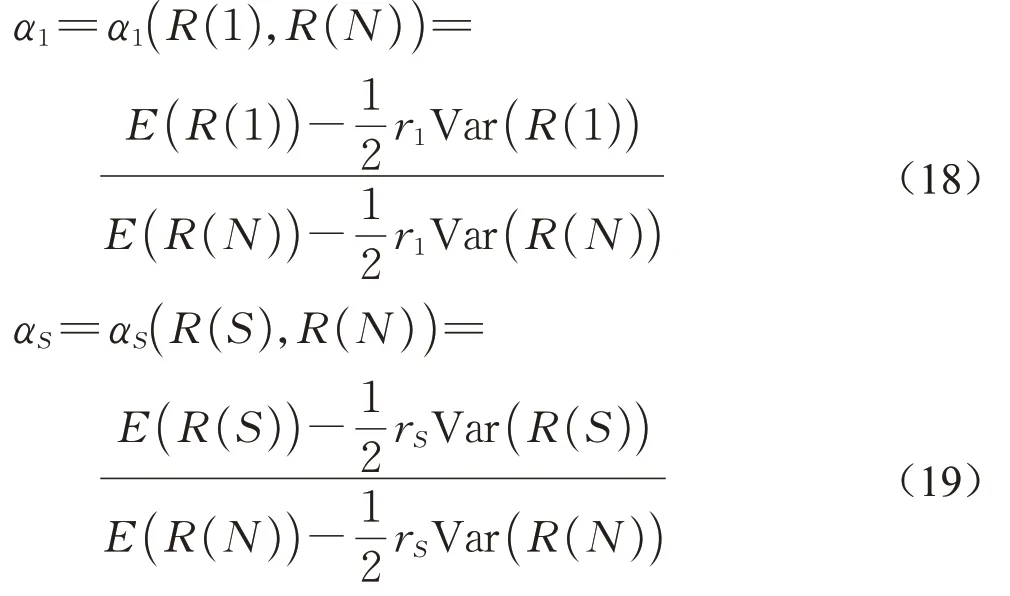
为了求解可以假定：

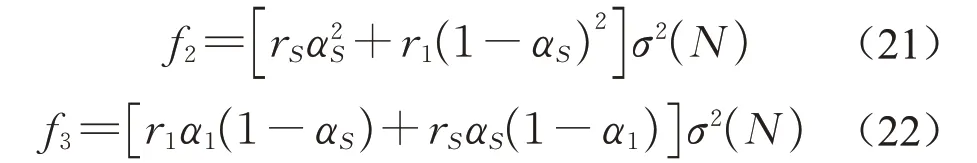
PPP模式下城市更新项目的风险溢价对概率的一阶最优条件可以表示为以下非齐次线性方程组：

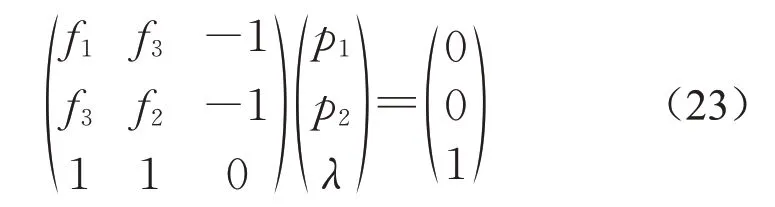
按照PPP模式下城市更新项目的风险溢价非齐次线性方程组特征，当D=f1+f2-2f3≠0时，有唯一解，得

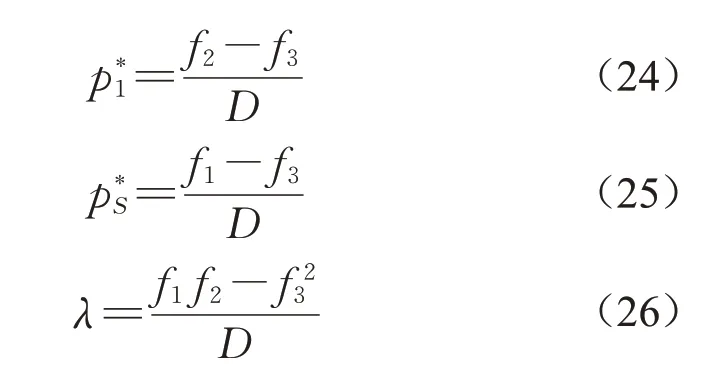
同理，针对私营部门联盟内部的风险分担模型建立拉格朗日方程并求解可得私营部门S内的风险分担比例分别为

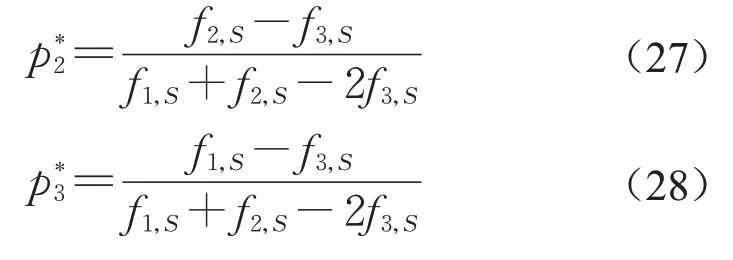
其中，

因此，对于整个城市更新项目而言，政府部门、专业运营公司和投资公司三方的风险分担比例为，由此可以保证PPP模式下城市更新项目各方的稳定合作。

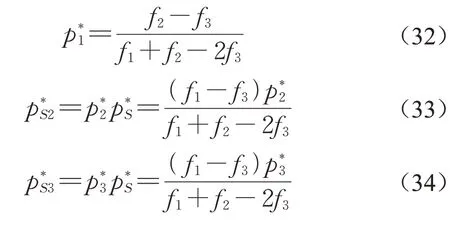
3 算例分析

上海市某小镇PPP项目是上海市较早落地实施的新型城镇化PPP项目，项目投资规模预期为170亿元，项目建设周期约10年。该项目符合城市更新的可持续性理念，强调以人为本，力争通过“城中村”改造等一系列工程来改善居民的生活状况和提高生态环境水平。PPP模式下城市更新不能由政府唱独角戏，PPP模式下城市更新的运作模式有政府开发、开发商主导、政府和开发商合作3类。该城市更新PPP项目选择了政府与私营部门合作开发模式，项目参与方包括公共政府部门，以及由专业运营公司和投资公司组成的联合体。

假设该小镇城市更新项目的某子项目在传统模式下，由政府部门单独实施项目并承担全部风险时的收益服从正态分布R(1)～N(8.0，1.0)（单位：千万元，下同）；若不参与该项目，专业运营公司A得到的保留收益为R(2)～N(6.4，1.4)，投资公司B得到的保留收益为R(3)～N(4.0，1.1)。若在PPP模式框架内进行开发，三方合作成立该子项目的项目部，通过权益投资并进行债务融资，发挥各自的优势和能力，项目获得的总收益必然大于双方单独的投资收益之和。假设PPP模式下该子项目收益服从正态分布R(N)～N(28.0，5.0)，其中专业运营公司和投资公司组成私营部门联盟，其收益远高于双方单独投资项目的收益之和，设为R(S)～N(14.0，1.5)。在该PPP项目面临的诸多风险中，长期的盈利风险是各方尤为关注的，政府部门对于长期盈利风险的风险厌恶程度要远大于私营部门联盟，因此各个参与方的规避系数不同。本文的算例主要讨论城市更新PPP项目的长期盈利风险。假设政府方、专业运营公司、投资公司对长期盈利风险的规避系数分别为r1=1.4，r2=1.0，r3=1.2，则私营部门联盟S的规避系数为rS=1.1。

由上述模型及已知数据可求得，对于整个子项目而言，政府部门与私营部门联盟S的无差异系数分别为

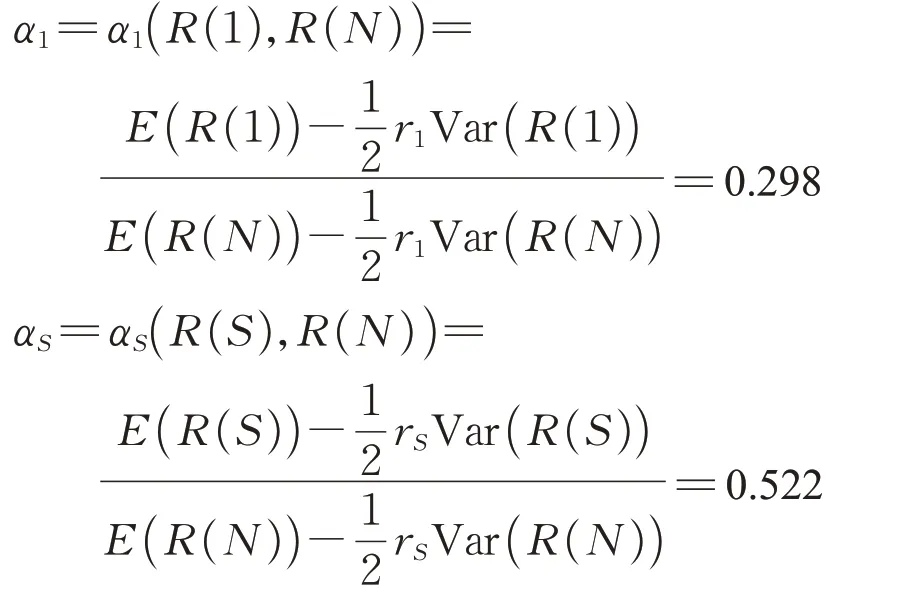
因此有

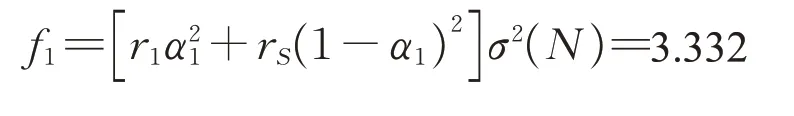
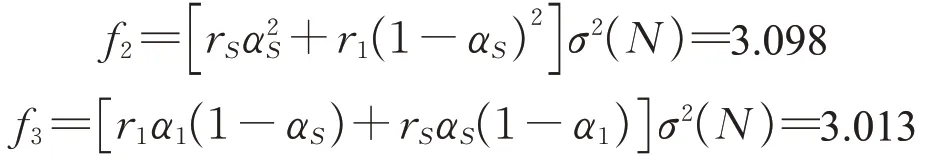
因为D=f1+f2-2f3=0.404 ≠0，所以

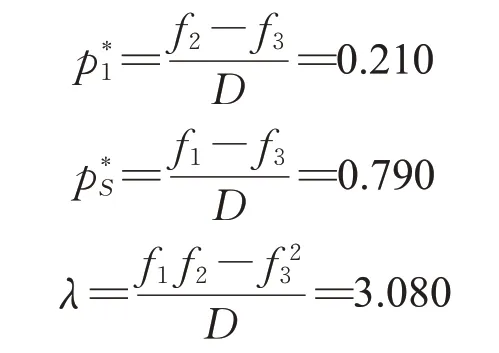
同理可以计算出，在联盟S内部，专业运营公司和投资公司的无差异系数分别为α2=0.430，α3=0.255，代入无差异系数和风险偏好系数可以得出f1，S=0.862，f2，S=0.950，f3，S=0.745，进而可以求出私营部门内部风险分担比例为p*2=0.637，p*3=0.363。表1和表2归纳了上述风险分担计算结果。

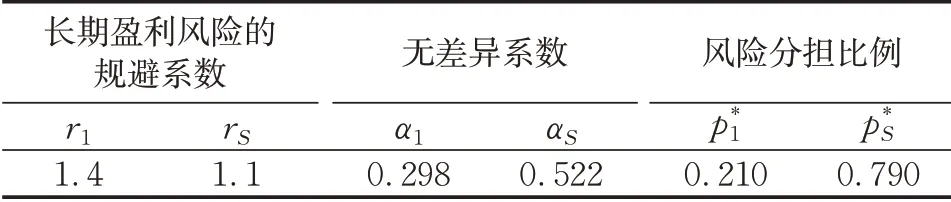
表1 政府部门与私营部门联盟S的风险分担计算结果Tab.1 Calculation results of risk sharing between government and private sector alliance S

表2 联盟S内部的风险分担计算结果Tab.2 Calculation results of risk sharing within alliance S

综上，经计算得此PPP模式下城市更新项目中，政府、运营公司、投资公司分担的最优比例政府和私营部门联盟、专业运营公司和投资公司的风险溢价分别为（0.678，0.862）、（0.222，0.187）千万元，项目的总风险溢价为1.540千万元；政府和私营部门联盟、专业运营公司和投资公司的确定性等价收益分别为（11.648，14.812）千万元、（7.399，6.192） 千万元，项目的总收益为26.460千万元。若不采用PPP 模式，政府和私营部门联盟风险溢价为（0.541，1.013） 千万元，总风险溢价为1.554千万元；政府和联盟S的确定性等价收益分别为（10.463，15.983） 千万元，总收益为26.446千万元。

因此，当项目存在长期盈利风险时，经城市更新PPP项目风险分担模型的计算，私营部门的部分风险会向政府部门转移。相较于不采用PPP模式，该城市更新项目的总风险溢价降低了0.014千万元，对应的总期望效用增加了0.014千万元，这表明本文提出的城市更新PPP项目风险分担模型是有效的，体现了城市更新PPP项目多方参与共同承担的特点，也实现了项目各参与方的共赢。

公共部门和私营部门通过具有约束的合约条款组成大联盟，专业运营公司与投资公司也是通过具有约束的合约条款组成私营部门联盟，以获取最大经济效益和社会效益。专业运营公司和投资公司单独参与项目的收益不如合作形成的私营部门联盟的收益，PPP项目风险分担模型可以根据两者的风险偏好对其收益和风险进行合理分配，从而保证私营部门合理投入资金、技术和管理人才，促进私营部门与政府的合作共赢。同时，PPP项目具有较长的周期，随着项目开发阶段和外在条件的改变，各参与方可以通过谈判方式，对原有的风险分担、利益分配进行调整，以确保项目能够顺利进行。PPP项目的各参与者是在合作中进行谈判、利益博弈，符合合作博弈的思想，可以从随机合作博弈理论找到最优的风险分担比例。

4 结语

本文以PPP模式下的城市更新项目为研究对象，基于随机合作博弈理论构建了政府、专业运营公司和投资公司三方参与的风险分配和经济效益最优的模型，使得城市更新PPP项目的三个参与方能够风险共担、利益共享。首先在充分尊重参与主体的风险偏好的基础上，建立了基于随机合作博弈理论的三方风险分担决策模型，然后结合Shapley值法求出了共担风险的最优分配比例，相较于现有的仅考虑两个参与方的类似研究更贴近实际情况，最后算例分析的结果表明，城市更新项目风险分担模型不仅可以确定参与各方共担风险的最优分配比例，而且风险转移之后的项目总风险相较于没有转移的情况下降了，项目的总收益增加了，提高了项目的合作效率。因此，本文提出的城市更新项目风险分担模型有助于兼顾各方利益，实现政府和私营部门之间的利益共享和合作共赢，也实现了私营部门内部的风险和利益的合理分担，为PPP模式下城市更新项目的风险管理提供新的可参考方法。

根据构建的理论模型和算例分析的结果，为进一步提升我国城市更新PPP项目的运作效率和经济效益，本文提出如下政策建议：

（1）政府应加强顶层设计，发挥其主导性作用，完善城市更新PPP项目的风险分担机制。目前我国的PPP项目风险分担机制仍存在着分担原则较为笼统、适用性较弱以及未充分体现项目实际特点等问题。此外，城市更新项目中各参与方的利益诉求各不相同，完善的顶层设计机制才能保证各方的利益，同时也是落实项目成果的前提和基础。虽然目前我国政策和相关优惠都向城市更新领域倾斜，但针对城市更新领域PPP项目风险分担的指导性较弱。因此，政府作为城市更新PPP项目的主体之一，应当发挥其主导、管理和促进的功能，加强顶层设计，进一步完善城市更新领域的PPP项目风险分担机制。

（2）健全城市更新PPP项目相关的法律法规体系，建立有效的奖惩机制。由于城市更新项目中的不确定性因素较多，仅靠合同难以约束利益主体的行为，而且本文的算例分析也表明，通过政府、专业运营公司和投资公司三方的利益博弈才实现了其在城市更新项目中的合作。健全的法律法规体系有利于约束各参与方的行为，确保各参与方按照合同约定共担项目风险。此外，建立灵活有效的激励机制和惩罚机制也有利于调动各参与方的积极性，刺激各参与方对城市更新PPP项目的管理与控制能力，协调推动城市更新PPP项目的建设实施。

（3）增强私营部门联盟的合作关系，发挥PPP项目的整体优势效应。算例分析结果表明，当私营部门内部的专业运营公司和投资公司组成合作联盟可以有效地防止政府部门依靠自身优势转移风险，从而更加合理地分担项目风险，促进合作稳定进行。因此，专业运营公司和投资公司需要及时协调私营部门联盟内部的各方关系，充分发挥各自的优势，增加联盟的稳定性以确保其竞争优势。而政府部门也应当主动加强与私营部门的合作关系，避免与私营部门的利益冲突，发挥多方整体优势效应，促进城市更新PPP项目的顺利推进。

本文的不足及展望主要有以下三点：

（1）本文的研究虽然考虑了政府、专业运营公司和投资方三个参与方，但得出的风险分担和经济效益最优模型主要是基于项目层面的合作者之间产出最优，并没有考虑公共价值，而实际中PPP项目的利益相关方有很多，未来可以在模型中加入改造区域的社区民众和银行等融资机构，进一步拓展多方共担的风险分担和转移之间博弈。

（2）本文的算例主要适用于政府、投资公司和专业运营公司三方参与城市更新项目的情况，但是仅考虑了长期盈利风险，没有对市场风险等其他风险进行探讨，今后的风险分担研究可以更加全面地考虑城市更新项目中的各类风险。

（3）风险分担模型中的风险变量是静态的，风险的分布概率是不变的，而许多风险是跨生命周期的，在各阶段的风险状况是不一样的，后续可以在动态风险管理方面做进一步研究，合理确定PPP模式下城市更新项目各个参与者风险偏好、期望报酬率、风险承受程度和范围，针对不同阶段动态地调整风险变量，建立动态的风险分担模式。

作者贡献声明：

杜学美：提出选题，设计论文框架，管理和协调整个研究过程和论文撰写过程。

李美菱：理论模型推导，算例分析计算，论文修订。

黄玉洁：文献梳理，论文撰写。

唐 星：调研，论文撰写。