凹坑板式空气预热器的传热特性及多目标优化

吴俐俊， 韦增志， 梁星原， 白书诚

（同济大学 机械与能源工程学院，上海201804）

对能量进行梯级利用是电站节能减排、降本增效的重要手段，空气预热器是电站进行能量梯级利用不可或缺的设备之一。目前其主要形式有回转式、管式和翅片管式［1］。工程实践中发现，回转式换热器结构复杂、耗电严重［2-3］，管式和翅片管式效率低、体积大，且易积灰堵塞［4-5］。结构紧凑、流动性能好、可模块化安装的板式换热器成为较合适的解决方案。

凹坑板式换热器的性能主要体现在传热和流阻两个方面，研究表明：凹坑可强化传热主要是由于凹凸结构的流场形成周期性的涡漩和二次流，近壁边界层内流动特性被改变，从而强化传热［6］；同时，这种结构的湍动能损耗更小，凹坑内部摩擦阻力在底部作为一种附加动力有推动效应［7］，具有减阻作用。因此，结构合理的凹坑结构可达到即强化传热又减小阻力的效果。

Kim等［8］在高雷诺数下研究了3种强化换热方式的传热流阻性能，分别是冲击、肋片和凹坑，得到在相近的增强换热效果下，凹坑的阻力损失最小。Chyu等［9］研究了叉排凹坑局部换热与雷诺数Re之间的关系，球面和泪滴形的凹坑结构使换热增强了两倍，而压力损失仅为翅片结构的一半。Burgess等［10］研究了凹坑深度对综合换热性能的影响，发现换热因子随着深度增加近似线性增大，阻力因子随着Re数的增大几乎不变，通道高度对换热和阻力的影响不显著，在凹坑深度大时综合传热性能更佳。Moon等［11］用液晶测温技术探究凹坑的通道高度对换热和流动特性的影响，发现板片间的通道高度对换热和压损影响很小。Samad等［12］对凹坑间距和凹坑投影直径之比采用多目标优化法进行优化，优化模拟结果显示：随着凹坑深度的增加，换热能力增大；凹坑间距减小，传热速率增大。王光辉等［13］对凹凸板的几何结构进行多目标优化分析，得到在其设定结构参数范围内的最佳组合。本文以凹坑强化换热技术［14-18］为理论基础，采用全焊接型凹坑板式换热器为空气预热器，在试验的基础上基于Workbench Fluent对凹坑板片进行数值模拟与结构优化，得到多因素交互作用下的换热与流动特性，弥补了单元模拟不能充分反映各结构参数协同变化与优化目标函数之间关系的不足，得到最优结构参数组合。

1 凹坑板式空气预热器计算模型

1.1 物理模型

凹坑板式空气预热器的芯体物理模型如图1所示，图示有3层高温烟气流体通道，两层低温空气流体通道。烟气流道由椭圆和条形两种结构类型组成，冷热流体呈叉流换热。本次模拟优化针对烟气条形通道的结构参数进行，所选取的计算区域为一个完整的烟条形通道，如图2所示。通道局部细节放大如图3所示，单板片的实物如图4所示。

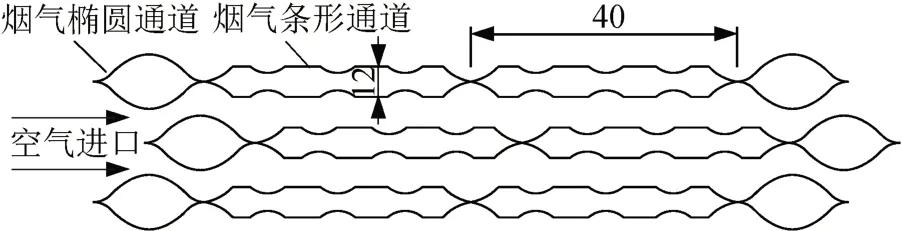
图1 凹坑板式空气预热器芯体结构示意图（单位：mm）Fig.1 Schematic diagram of core structure of plate air preheater with dimples (unit: mm)

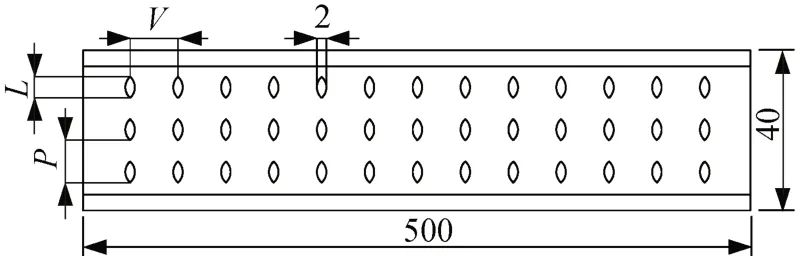
图2 烟气条形通道俯视图（单位：mm）Fig.2 Top view of flue gas strip channel (unit: mm)

图3 烟气条形通道局部放大图Fig.3 Partial enlarged view of flue gas strip channel

图4 凹坑板式空气预热器板片实物图Fig.4 Physical picture of plate air preheater with dimples

凹坑的几何结构变量参数包括凹坑长轴L、凹坑深度H、凹坑横向间距P，以及凹坑纵向间距V。凹坑排布为3列21行。

设计参数的约束空间如表1所示。

表1 设计参数的变化范围Tab.1 Variation of design parameters

1.2 数学模型

为简化流体的流动与换热模型，假设：①板片的物性参数为常数，不随温度的变化而变化；②流体为各向同性且为连续介质，忽略重力作用；③流体为牛顿流体，流体与固定壁面接触时的速度为零，即无滑移的速度边界条件；④忽略流体流动时由于黏性耗散作用产生的热效应；⑤忽略高温气体热辐射对换热性能的影响。各控制方程见文献［13］所示。

1.3 目标函数

在进行多目标优化研究时，通常要选定优化的目标函数，即以该函数为量化目标对各个可控变量进行调整优化从而达到最优解。采用摩擦因子f来衡量换热器的流动性能，f因子忽略了当量直径和长度的影响，f因子越小，介质流动阻力越小，板片流动性能越好。努塞尔数Nu通常用来衡量换热能力的大小，其值越大则换热效果越好。采用JF因子来评价换热器的综合性能。

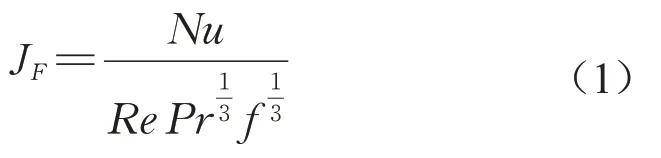
式中：Pr为普朗特数。

2 数值计算及试验验证

2.1 边界条件设置及计算方案

对烟气条形通道进行数值求解，边界条件为：①入口设置为速度进口，流速为6 m·s-1，温度为673 K；②出口设置为压力出口；③布置有凹坑的上下两侧壁面设置为303 K的定壁温。湍流模型采用标准的k-ε模型，速度和压力的耦合采用标准SIMPLE算法，壁面处采用增强壁面函数法，对流项和扩散项的离散采用二阶迎风格式。当网格总数约120万且步长为1.4 mm左右时，Nu的变化率为4.2%，ƒ几乎不再改变，说明此时网格精度已经满足计算要求。

为了能够获得最佳的空间覆盖面和丰富的数据信息，使得抽样样本能够代表优化变量空间，进而得到优化变量与目标函数之间的映射关系，需要对此进行试验设计。正交设计是一种高效经济的研究多因素多水平的试验设计方法，可以满足均匀分散、齐整可比的方案要求。采用正交设计助手Ⅱ3.1设计正交试验方案［19］，共设计25组试验，计算结果如表2所示。

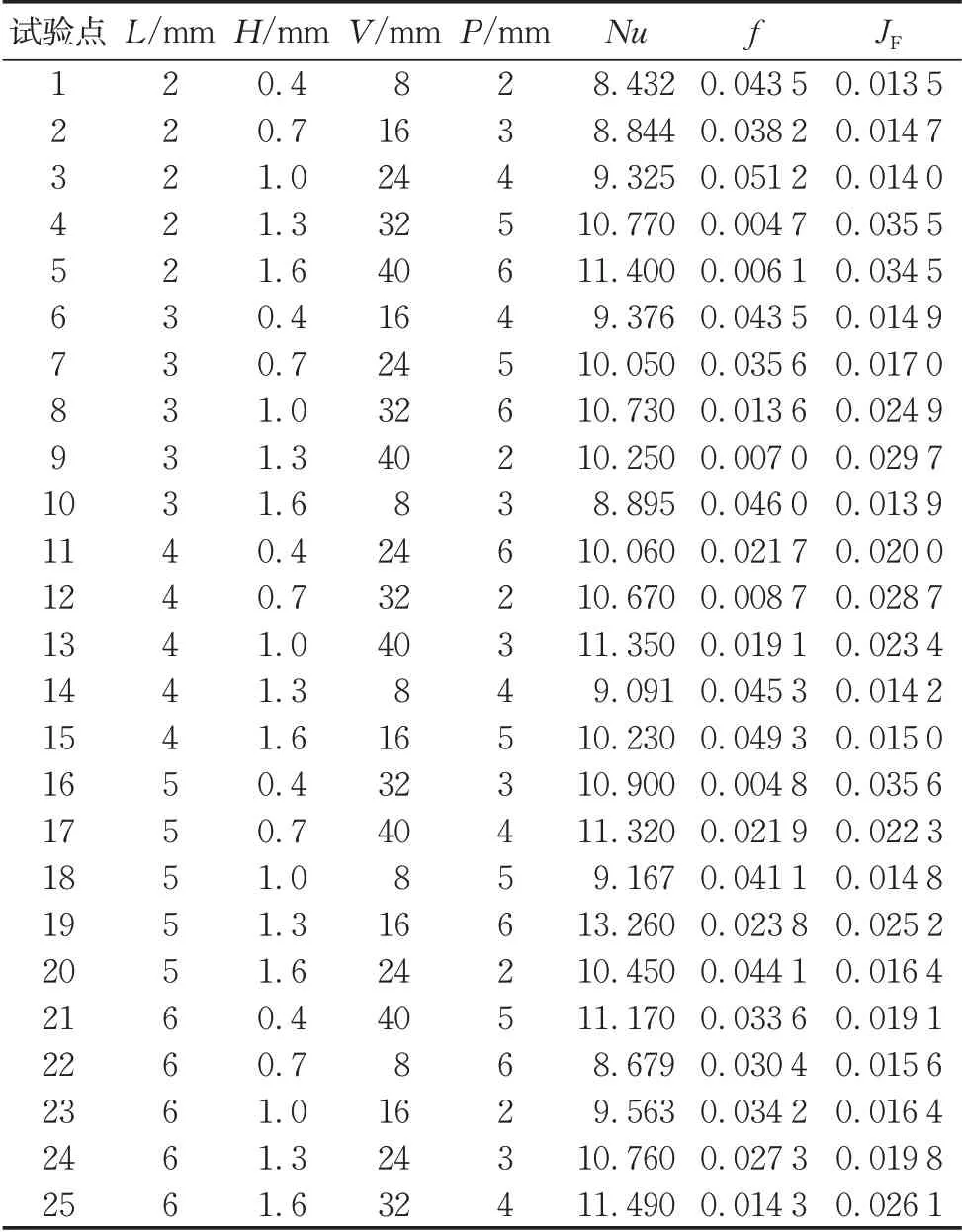
表2 设计方案计算结果Tab.2 Calculation results of design plan

2.2 试验验证

为了对计算模型和数值模拟的准确性进行验证，搭建了凹坑板式空预器的试验系统。该系统由烟气发生装置、凹坑板式空预器、离心式空气风机、烟气二次冷却器和测量设备组成，所搭建试验台如图5所示，系统图如图6所示。烟气发生装置主要由1台天然气燃烧器和1台空压机组成，所需的烟气由天然气燃烧产生的高温烟气和空压机送入冷空气混合而成。凹坑板式空预器芯体通道长度为500 mm，板间距12 mm，14层烟气通道，15层空气流道，由28张板片错位堆叠焊接而成。冷却空气由离心式空气风机加压送入凹坑板式空预器与高温烟气换热后排出。测量设备包括热电偶、电容式压差变送器、涡街流量计。由于高温烟气在凹坑板式空预器内换热后的温度仍高于涡街流量计的工作温度，因此在凹坑板式空预器的烟气出口管道安装1台烟气二次冷却器以再次冷却烟气，使烟气的出口温度在涡街流量计的工作温度范围内，冷却介质为水。

图5 凹坑板式空气预热器试验台Fig.5 Experiment device of plate heat exchanger with dimples

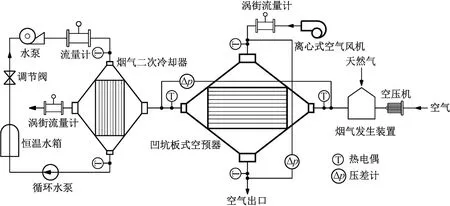
图6 试验系统图Fig.6 Diagram of experimental system

试验中，通过调节空压机和燃烧器助燃风机的工作频率来调控烟气的温度和流量，由离心式空气风机调控冷却空气入口流量，空气进口温度为恒定室温30 ℃。以烟气入口温度作为横坐标变量，控制试验参数与模拟参数在空气与烟气入口处的温度和速度一致，对比两者在烟气侧和空气侧的出口温度及压降，结果如图7和图8所示。

由图7a可以看出，烟气出口温度的试验值总是小于模拟值，原因是试验中高温烟气通过凹坑板式空预器时对外界环境散热致使热量散失，因此其出口温度较模拟值低。从现场设备布置分析，烟气对外散热可能是由于换热设备和管道的保温效果不够理想。由图7b可以看出，烟气侧压降的试验值总是大于模拟值，原因是数值模拟的物理模型经过了合理简化，现场试验的凹坑板式空预器经过多层板片堆叠焊接而成，受限于装配焊接工艺，现场设备的局部阻力较数值模拟物理模型大，因此其压降大于模拟值。由图8a和图8b可以看出，空气出口温度的试验值稍大于模拟值，空气侧压降的试验值大于模拟值，将二者结合分析，该现象产生的原因可能是空气在现场试验设备中受到的局部扰动更强烈，一方面强化了空气侧的换热，使得空气出口温度升高，另一方面也增大了压降。结合图7和图8分析可知，现场试验设备的换热性能较模拟时强，其原因为试验设备的实际流道情况更复杂，由装配焊接工艺及封装换热芯体壳体所造成的影响对流体的扰动更大，因此其换热能力增强，但也因此造成更大的试验值压降。综上模拟和试验结果的对比可以看出，烟气侧的温度和压降、空气侧的温度和压降在试验与模拟中的误差基本在10%以下，工程上这种误差在可接受范围内，因此可以认为对凹坑板式空预器的物理模型与数学模型的建立合理。

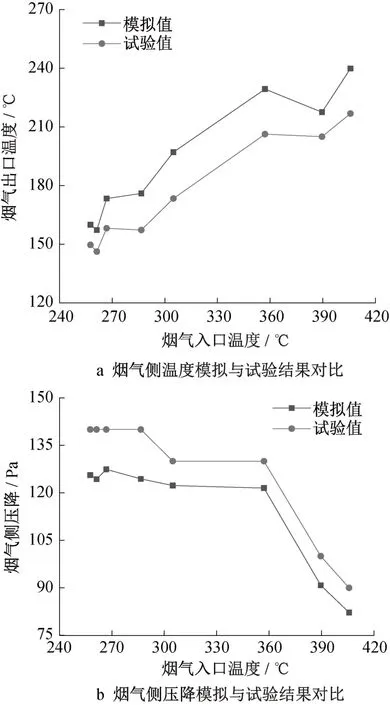
图7 烟气侧温度和压降的模拟与试验结果对比Fig.7 Comparison of simulation and experimental results of temperature and pressure drop on flue gas side

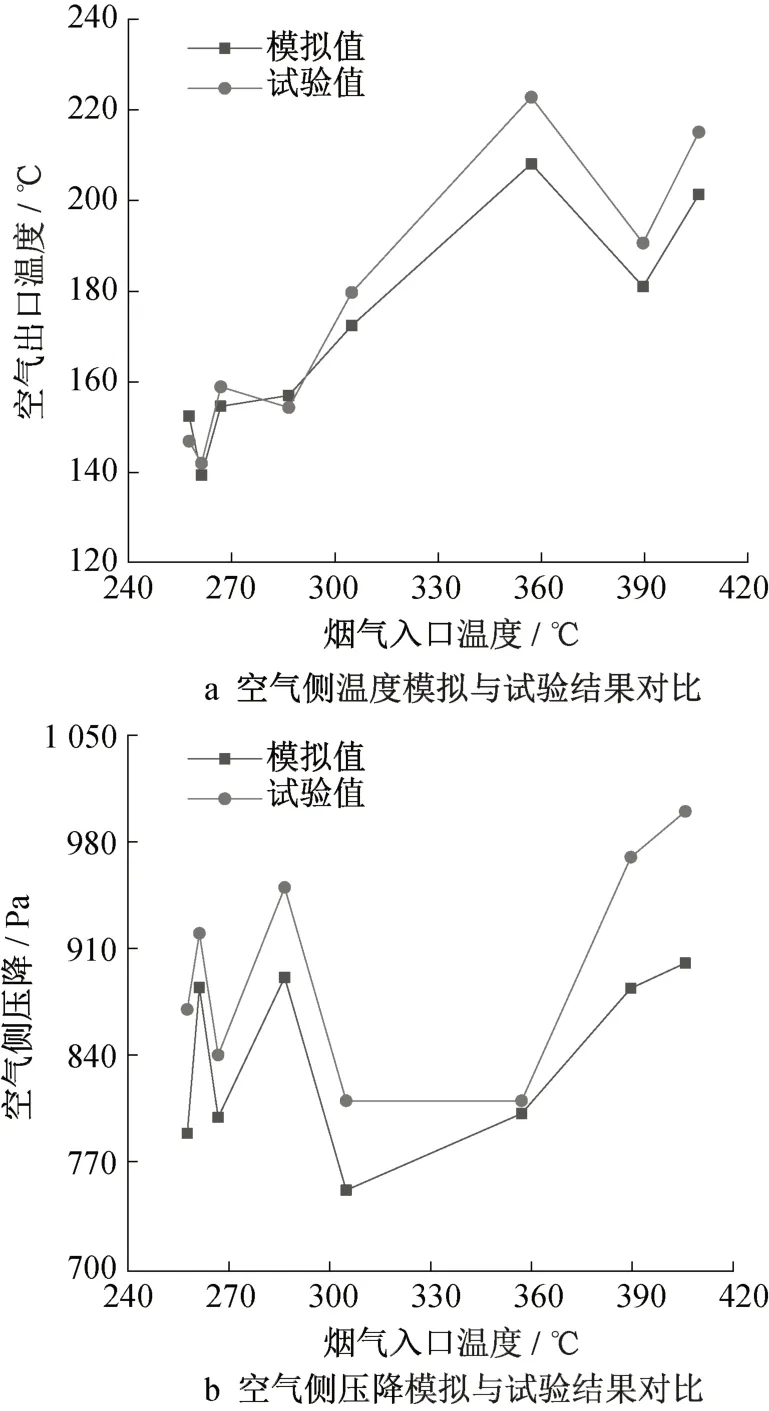
图8 空气侧温度和压降的模拟与试验结果对比Fig.8 Comparison of simulation and experimental results of air side temperature and pressure drop

3 优化结果及分析

3.1 参数敏感度分析

在4个特征结构参数中，为明确各参数对凹坑板性能的影响，对各参数进行敏感度分析。参数敏感度由输入设计参数、输出目标函数的拟合结果得到，以S=（Fmax－Fmin）/Fave为表达式［20］，其中Fmax、Fmin分别为目标函数的最大和最小值，Fave为目标函数均值。若目标函数与变量参数呈正相关则敏感度为正，反之为负。在敏感度柱状图中，可得到各输入参数对目标函数的敏感程度大小，柱状图绝对高度值越大，该参数对目标函数值的影响就越大。

从图9中可以看出，各目标函数对凹坑纵向间距V的敏感度最大，即当纵向间距V改变时，各目标函数值的改变量最为显著，其次是凹坑长轴L，再次是凹坑深度H，最后是凹坑横向间距P。从图9a可知，纵向间距对传热性能影响最大，凹坑长轴对其也有重要影响，而横向间距的敏感度最小且为负值。这说明纵向间距和长轴的大小对来流扰动影响很大，纵向间距的疏密可造成来流处于连续密集的凹坑涡流扰动中，从而影响传热性能。从图9b可知，纵向间距对流动性能的影响最大，其次是凹坑长轴，二者对f的敏感度都是负值，凹坑深度和横向间距的影响较前二者都弱，但其影响是正相关。由于纵向间距和长轴可在一定程度上强化对流传热，因此其流动性能会有所削弱。从图9c可知，纵向间距和凹坑长轴对综合传热性能有着较大的正相关影响，凹坑深度和横向间距的影响较小且敏感度为负值。对综合传热性能的影响而言，凹坑之间的结构参数横向间距和纵向间距比凹坑自身的结构参数深度和长轴的影响大。

图9 结构参数对板片性能的敏感度分析Fig.9 Analysis of sensitivity of structural parameters to plate performance

3.2 凹坑纵向间距V对流动传热性能的影响

为使分析结果更具普适性，把凹坑自身的结构参数深度H与长轴L设为一对，即深径比；凹坑之间的结构参数横向间距P与纵向间距V之比设为一对，即横纵距。从上述敏感度分析中可知，对流动传热性能影响较大的参数有纵向间距V和长轴L，选取二者进行综合分析。

从图10a可以看出，摩擦因子ƒ随着V的变化而变化，最大值与最小值之比超过4倍，横向间距P越大，ƒ越小，凹坑的深径比影响了ƒ的走势，其比值越大，f也越大。V≈32 mm时有极小值出现，当V小于32 mm时，随着V增大，f减小，造成这种现象的原因是当沿流动方向的纵向间距过小时，凹坑局部涡流扰动强烈，在密集的凹坑内产生反转流体消耗湍动能，各凹坑间的流体相互扰动损耗，进而增大了流阻。由图10b可以看出，当V小于16 mm时，Nu随V的增大而迅速增大，V为16 mm时Nu达到极大值，当V大于16 mm后，Nu随V增大而缓慢减小。其原因是沿流动方向上凹坑的纵向排列间距由密集到稀疏变化过程中，密集时流体在凹坑中的充盈度不高，相同的板长和凹坑数量下，其对流体边界层的扰动未被换热面充分利用，间距增大变稀疏后，该问题得到缓解，因此当V小于16 mm时，Nu会随V的增大而迅速增大。但纵向间距增大至一定数值后，即凹坑分布更稀疏时，此时凹坑对流体的扰动减小，流动边界层增厚，因此Nu随V增大便开始缓慢减小。横向间距P对换热性能影响较小，而凹坑长轴对其有较大影响，小深径比下Nu较大。从图10c可以看出，JF随着V的增大而增大，但增速逐渐放缓；凹坑的深径比增大，JF降低，其原因是凹坑越深，越容易在其内部形成流动死区，使得流动阻力增大，边界层增厚，不利于换热，从而JF降低。

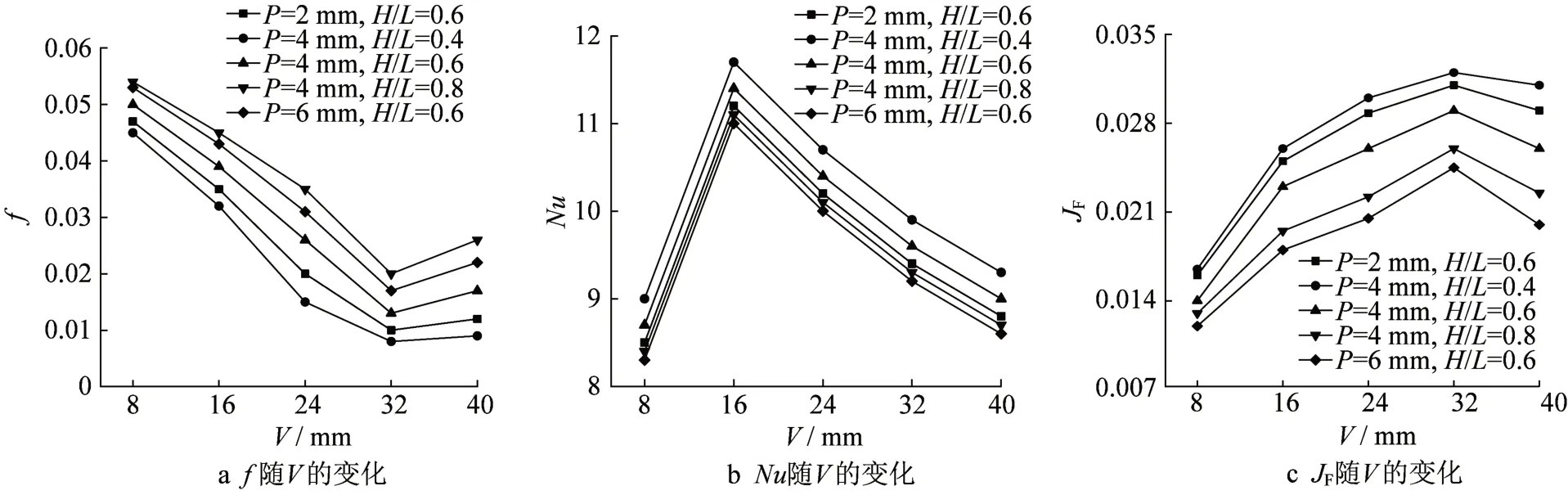
图10 凹坑板的传热流阻性能随凹坑纵向间距的变化Fig.10 Heat transfer and flow resistance performance versus longitudinal spacing of dimples

3.3 凹坑长轴L对流动传热性能的影响

从图11a可以看出，凹坑长轴L增大，流动性能增强，这是由于随着深径比的减小凹坑越趋扁平，则回流所形成的涡旋也越趋扁平状，这时大部分流体沿凹坑边缘快速旋转流出，凹坑的旋涡中心不易出现滞流，因而流动性能较好。从由图11 b可以看出，长轴L增大，换热性能下降，原因是较扁平凹坑内回旋流体较少且流速相对较快，涡流扰动强度减弱，能量与动量未能及时充分交换，因而性能下降。从图11 c可以看出，增大L可增强流动性，但也会削弱换热能力。L小于4 mm时，JF随L的增大而增大，L大于4 mm后，JF随L的增大而减小，在L≈4 mm处取得JF的最优值。

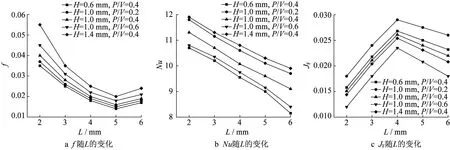
图11 凹坑板的传热流阻性能随凹坑长轴的变化Fig.11 Heat transfer and flow resistance performance versus long axis of dimples

3.4 三维响应曲面分析

敏感度分析仅考虑了单一变量对优化目标的影响，具有一定局限性。本文在25组正交试验数据基础上，通过非参数回归法生成更全面直观的三维响应曲面图，研究变量参数两两协同作用对努塞尔数Nu和摩擦因子ƒ的影响。

从图12a、12b和12c中可以看出，当深度H小于1.2 mm时，板片的传热性能随着H的增大而迅速增大，并在H等于1.2 mm时达到峰值，随后降低，说明凹坑过深或过浅对传热都有不利影响。过浅的凹坑类似于平板换热，而过深的凹坑既增大了内部涡流动能损耗，也增厚了凹坑内的边界层造成流动死区，不利于强化换热。从图12a、12e和12f可以看出，当长轴L小于4.5 mm时，传热性能随着L的增大而增大，L大于4.5 mm时，传热性能开始降低，存在较明显传热性能峰值取值区，与凹坑深度H规律相似。在图12c、12d和12f中，随着纵向间距V的变化，Nu敏感度大且有最宽的值域范围，与不同参数协同作用下存在单个或多个峰值区间，原因是纵向间距V对传热性能影响最大，其值的改变较容易与其他参数的变化形成显著的复合叠加效果。在小横向间距、大纵向间距下板片传热性能好，小长轴、大横向间距下传热性能差，小横向间距、大深度下传热性能最好，小长轴、小纵向间距下传热性能最差。各变量参数与Nu协同作用下都出现了孤峰值说明，对于两两协同作用下的L、H、P和V的值对增强换热性能存在最优解区间。

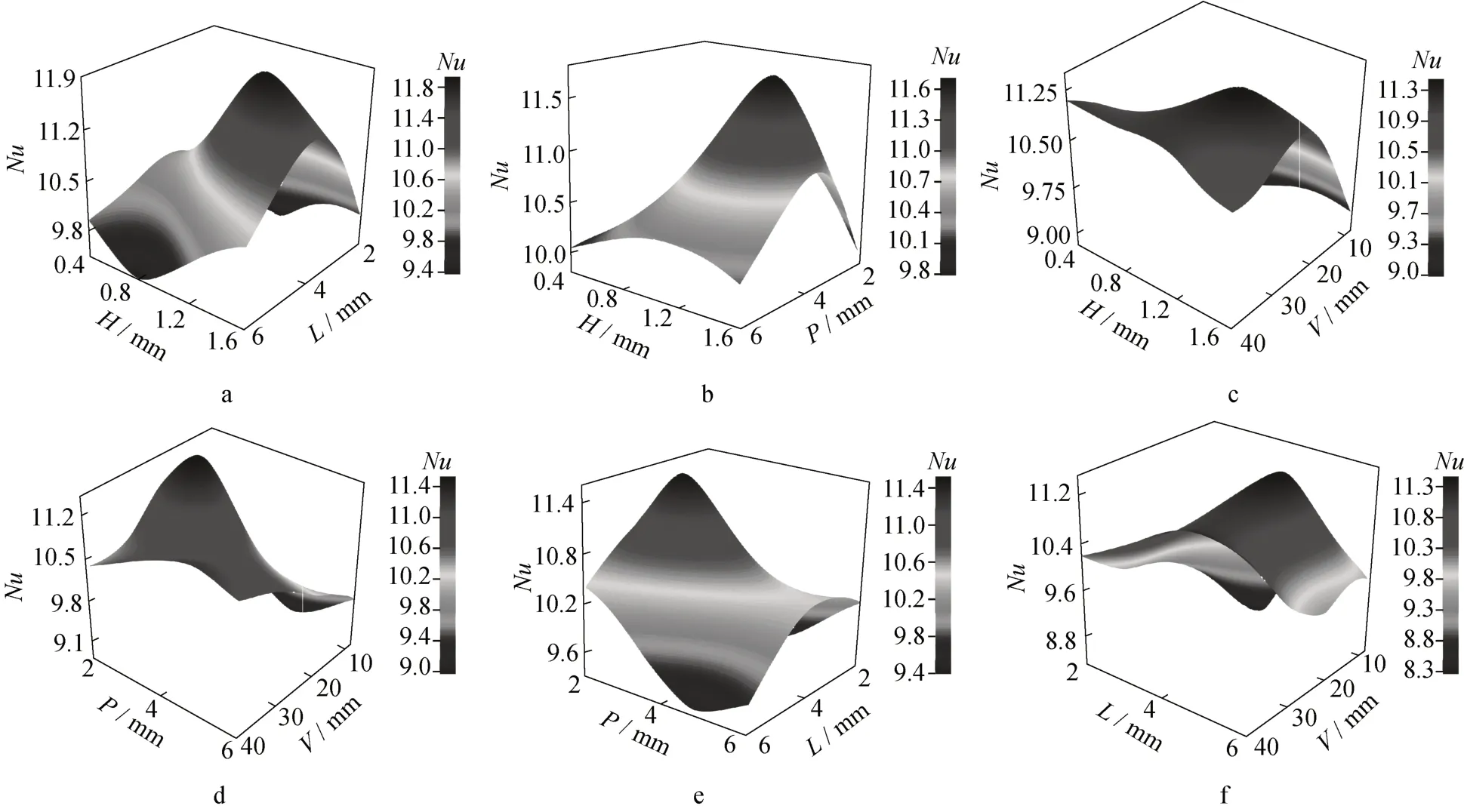
图12 L、H、V、P对目标函数Nu的响应曲面Fig.12 Response surface of L, H, V, and P to objective function Nu

图13反映了凹坑长轴L，深度H，纵向间距V以及横向间距P两两协同作用对摩擦因子f的影响。从图13a、13d和13f可以看出，小长轴下板片流动性能差，小横向间距、大长轴下凹坑板阻力性能好，在小纵向间距和小长轴下流动性能最差。图13c、13e和13f表明，大纵向间距下阻力性能好，H、P、L随V的减小流动性能近乎呈单调线性下降，大纵向间距、小深度下流动性能最好。相比于传热性能的响应曲面图12，图13中只有图13b出现了孤峰值，其余峰值都在边界上，表明凹坑板阻力性能随结构参数变化呈现出一定单调性、可预测性。

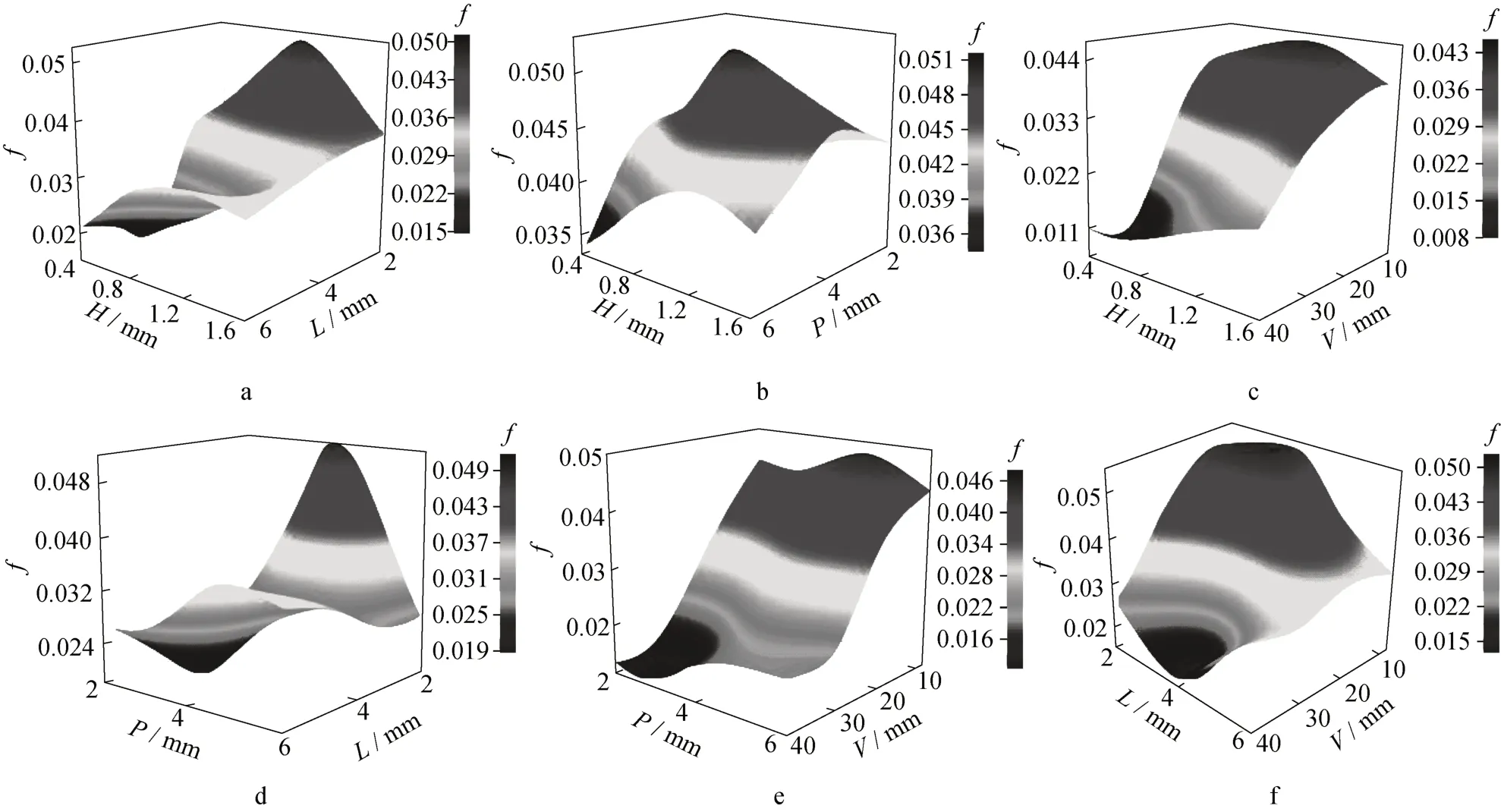
图13 L、H、V、P对目标函数ƒ因子的响应曲面Fig.13 Response surface of L,H,V, and P to objective function ƒ

3.5 遗传算法优化参数组合

遗传算法是模拟生物进化论的自然选择和遗传学机理的数学计算模型，由于其具有全局搜索策略和寻优过程不依赖于梯度信息而只需要影响寻优方向的目标函数和相应的适应度函数等优点［21-22］，是研究多目标优化问题的有效方法。

基于Workbench Fluent模拟计算的25组数据通过Workbench Fluent平台建立输入设计变量与输出目标函数的适应度关系，将待优化变量参数凹坑长轴L、深度H、纵向间距V以及横向间距P作为基因合成一个独立的染色体并进行编码，设置优化范围L=2～6 mm，H=0.4～1.6 mm，V=8～40 mm，P

=2～6 mm，采用完全随机法对种群进行初始化，初始种群大小取50。设定最大迭代次数为200次，交叉概率为0.8，变异概率为0.2，以适应度关系作为评价标准，即要满足优化目标函数中较大的Nu和JF因子、较小的f因子，符合条件则输出结果，不满足则再进行选择、交叉和变异计算，产生新的群体。根据优胜劣汰法则，不断筛选得到更加优化的群体，最后选择适应度高的3个个体作为最优解，如表3所示。

表3 最优参数组合及其目标函数值Tab.3 Optimal parameter combination and its objective function value

4 结论

以全焊接型凹坑板式空气预热器为对象，正交设计试验方案，在试验所验证的工况范围内（空气进口温度30 ℃，烟气进口温度255～405 ℃），采用Workbench Fluent数值模拟凹坑板片特征结构参数对传热流阻性能的影响，基于敏感度分析、响应曲面法、多结构参数组合下的传热流阻特性曲线和遗传算法等分析工具进行综合评判，得到以下结论：

（1）多因素协同作用下，凹坑之间的结构参数横纵距比凹坑自身的结构参数深径比对换热器性能影响大。

（2）凹坑的纵向间距对板片的传热性能影响最大，其次是凹坑长轴，最后是凹坑深度。凹坑的横向间距对其影响最小且为负相关。

（3）凹坑的长轴对板片的流动性能影响最大，其次为纵向间距，横向间距对其影响最小。

（4）凹坑的纵向间距和凹坑长轴对板片的综合热性能影响较大，横向间距和深度对其影响较小。

（5）对换热性能而言，凹坑的结构参数对其影响呈两面性，换热能力随某一结构参数的增加或减小并非是一致单调性的变化；对流动性能而言，凹坑的结构参数对其影响呈现一定规律性，流动性能与某一结构参数的增加或减小呈现近似单调性或可预测的变化。

（6）在凹坑板式空预器给定的结构参数范围内，基于遗传算法得到3组较优结构参数组合，分别是①L=2.02 mm、H=1.44 mm、V=36.55 mm、P=5.93 mm；②L=2.16 mm、H=1.45 mm、V=39.15 mm、P=5.71 mm； ③L=2.30 mm、H=1.50 mm、V=37.06 mm、P=5.94 mm。

作者贡献声明：

吴俐俊：整体方案设计。

韦增志：落实设计方案，计算模拟与论文撰写。

梁星原：试验平台搭建。

白书诚：开展试验操作。