基于热-水-力数值模拟的饱和正常固结黏土热压缩现象

张 锋， 熊勇林

（1.名古屋工业大学 土木工程系，名古屋 466-8555；2.宁波大学 土木与环境工程学院，浙江 宁波 315211）

随着核废料地下存储、二氧化碳地下封存、地热资源开发、石油开采、高压电缆埋设、能量桩应用等工程的大量兴起，在研究岩土材料在常温条件下本构关系的同时，研究高温对岩土材料力学特性的影响已经成为岩土工程学科的一个重要领域，也是目前国内外研究中一个十分困难而又迫切需要解决的问题。例如核废料的地下存储就是将核废料埋置于深度达数百米的稳定地层中，使之与生物圈永久隔离。但由于核素在长期衰变过程中会缓慢释放热量，导致处置库周边土体温度逐渐上升，引起土层中应力场、位移场及渗流场的变化，进而影响放射性核素的迁移规律。故地下永久隔离的重要条件之一是确保核废料周围土体在高温荷载作用下长期稳定［1-2］。已有大量的试验结果表明，温度对土体水力特性行为的影响是不可忽视的［2-4］。因此，开展土体在热-水-力耦合作用下的相关研究，具有明确的需求背景与应用前景。

迄今为止，许多学者针对温度对岩土材料力学特性行为的影响进行了大量的研究。Hueckel等［5］对黏土进行了不同恒温条件下的三轴压缩剪切试验，结果表明，土体材料的剪切强度随着温度的升高而降低，应力应变关系由脆性变为延性。而另一些研究却得出了相反的试验结果。Cekerevac等［6］和Kuntiwattanakul［7］针对高岭土的试验结果却表明，温度上升也可以导致土体材料剪切强度增加，应力应变关系由延性转为脆性，温度升高使土体材料临界状态参数M增加。Campanella等［8］和Cekerevac等［6］在不同温度条件下进行了饱和土的固结试验，发现土体的压缩斜率λ与回弹斜率k不随温度变化而变化；随着温度的升高，土体的前期固结压力呈减小趋势。同时Cekerevac等［6］研究发现，升温引起的土体体积应变与超固结比（OCR）有关，随着OCR的增大，土体体变将由热压缩向热膨胀转变。

此外，基于室内单元试验，许多热弹塑性本构模型也相继被提出。 Cui等［9］从试验结果出发，在剑桥模型的应力屈服面的基础上，引入新的温度屈服面，该屈服面随温度上升而收缩，从而得到温度荷载-硬化参数（塑性体积应变）的关系，建立了一个饱和土体的热弹塑性本构模型。Yao等［10］考虑温度对土的先期固结压力与临界状态线的影响，提出相应的发展式，得到可以考虑温度影响的饱和黏土热弹塑性本构模型。 Zhang等［11］基于温度引起的“等效应力”概念，在平均应力p与偏应力q空间下提出了饱和软岩的热弹黏塑性本构模型，模型中只添加了一个线膨胀系数用来描述温度对土体力学特性的影响，同时该模型也被验证符合热力学定律。为了考虑中间主应力对岩土材料强度与变形的影响，Xiong 等［12］通过引入tij转换应力［13］，对Zhang等［11］的 结论进行了修正，并成功地将其应用到核废料地下储存工程问题的数值分析中。

众所周知，任何材料在温度升高时，体积都会发生膨胀，然而Cekerevac等［6］在对饱和正常固结黏性土进行加温时发现，土体体积并非发生膨胀，而是产生收缩。研究者在构建土体热弹塑性本构模型时，为了描述这一特征，将至少增加一个参数才能进行模拟。针对这一现象，Zhang等［14］通过采用热-水-力（THM）有限元程序对该室内试验进行了数值模拟分析，结果表明，室内加热试验仅是一个边界值问题，而并非土体的固有特性。然而，Zhang等［14］采用的计算模型尺寸比室内试验试样大一倍，这可能会对计算结果产生一定影响。

基于此，本文在Zhang等［14］研究的基础上，将计算模型尺寸改为与室内试验尺寸一样进行THM数值分析，并考虑了黏土渗透系数的影响。研究结果表明，室内土体加温试验结果所得到的体积收缩现象是由于土体在升温时，内部形成温度差，导致土体产生超孔隙水压而引发的。当提高土体渗透系数，土体内部不产生超孔隙水压时，土体将会发生热膨胀现象。换言之，土体在加热时仍然符合热膨胀这一普遍规律。本文研究成果将有助于合理构建土体热弹塑性本构模型。

1 热弹黏塑性本构模型

本文所采用的本构模型为Xiong 等［12］在tij转换应力空间下修正的热弹黏塑性本构模型，以下将对该模型进行简单介绍。详细推导可参考文献［12，15］。

该模型与剑桥模型一样，采用了联合流动法则，模型屈服函数表达式如下：

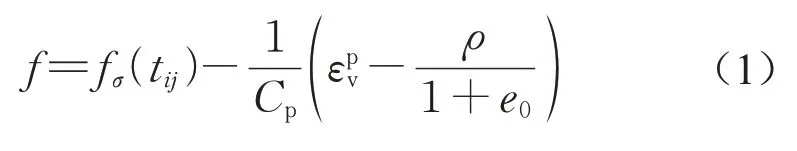
其中

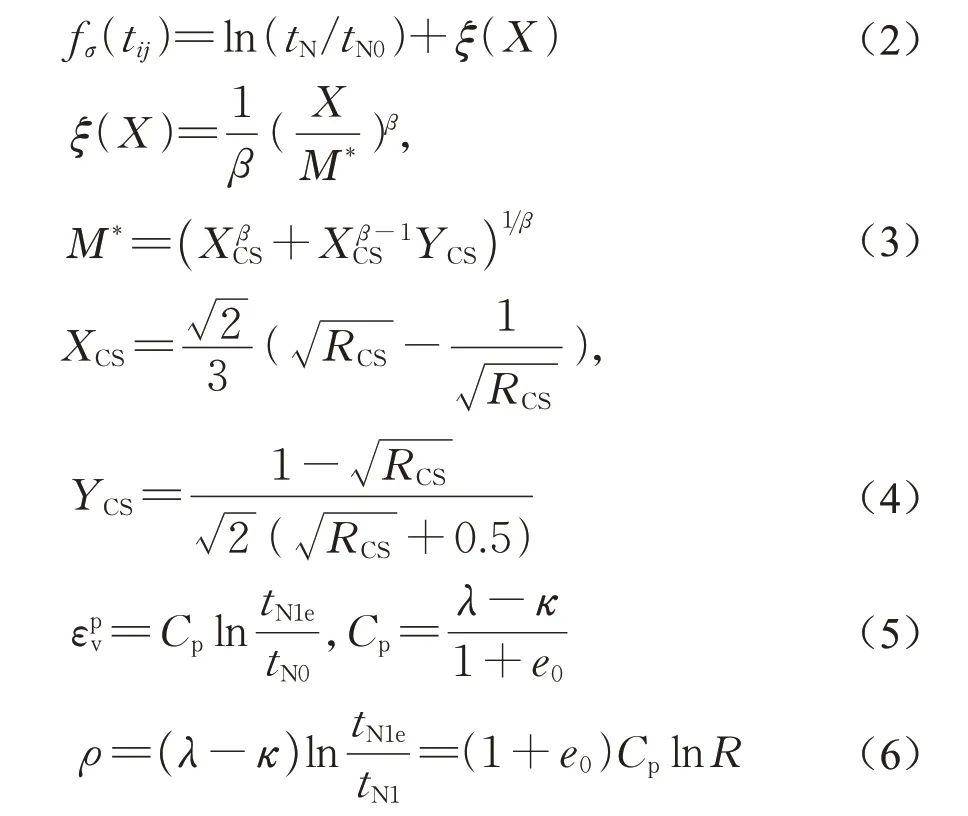
式（1）～（6）中：tN为在tij转换应力空间下的平均应力；X为剪切应力比；tN0为参考应力，通常取为一个大气压值，tN0=98 kPa；ρ为超固结状态与正常固结状态之间的孔隙比之差，如图1a所示；R为超固结比；M *为剪胀曲线在Y轴的截距，如图1b所示；e0为参考应力下的土体初始孔隙比；RCS为三轴压缩时主应力比σ1/σ3在临界状态下的值；λ和κ为土体压缩与回弹指数；tN1与tN1e分别为正常固结屈服面与下负荷屈服面与X轴的交点；β为屈服面形状控制参数；εpv为塑性体积应变。

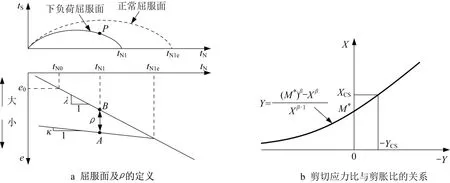
图1 下负荷屈服面、正常屈服面、ρ的定义及剪切应力比与剪胀比的关系Fig.1 Subloading yield surface, normal yield surface, definition of ρ ,and stress-dilatancy relation

对式（1）进行微分可得到

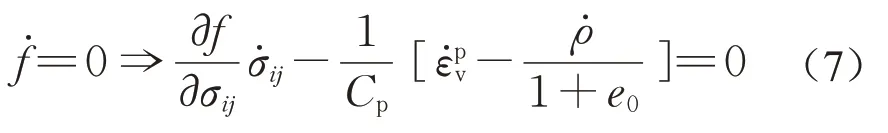
式中：σij为应力张量。

孔隙比差ρ的发展式表达如下：

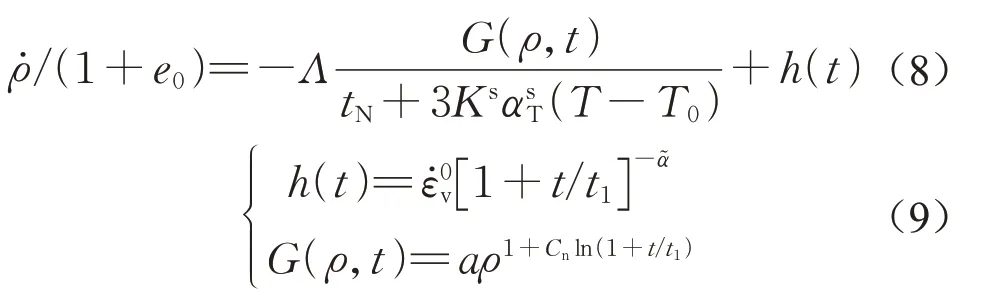
式（8）、（9）中：Λ为塑性因子；Ks为土体体积弹性模量；ε˙0v为t=0时的初始体积应变速率；t1为单位时间，用于标准化时间，通常取值为1；α~为时间依存参数，用于控制蠕变发展速度；Cn为应变速率依存性控制参数；T与T0分别为当前温度与参考温度；αsT为土体线膨胀系数；a为超固结状态发展速率控制参数。

模型中采用联合流动法则，塑性应变可由下式求得：

将式（7）、（8）与（10）代入式（6）中，可得

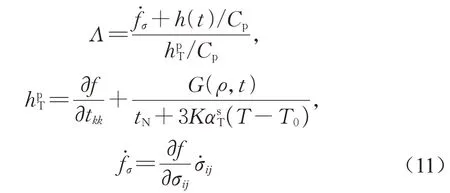
当土体处于蠕变（f˙=(∂f/∂σij)σ˙ij=0）状态时，可得到以下表达式：

模型中采用以下形式判断加卸载：

2 饱和黏土热固结试验数值分析

Cekerevac等［6］采用温控三轴试验设备，通过水浴对饱和黏土进行不同超固结比条件下的加热试验，试验结果表明，当超固结比为1（正常固结状态）时，温度引起的土体体积变化表现为热压缩。为了描述这一性质，学者在构建土体热弹塑性本构模型时将至少增加一个参数。然而，近年来，Zhang等［14］通过采用THM耦合有限元程序对其进行了数值模拟分析，结果表明，饱和正常固结黏土在加温时，由于热传导系数小，土体内部会产生不均匀温度，进而造成内部应力差，引起超孔隙水压增加，最终表现为热压缩。换言之，土体加热试验表现出来的热压缩现象并非为土体基本性质，而是边界值问题。但是，在文献［14］的计算中，模型尺寸比试验的试样尺寸大了一倍，这会夸大土体加温时试样受热的不均匀性。

本文在文献［14］的基础上，将模型的尺寸缩小到与试验中试样大小一样，并采用同一套THM耦合有限元程序对该问题进行进一步探讨分析，计算中所采用本构模型为上节介绍的热弹黏塑性本构模型，模型使用参数同文献［14］，见表1。

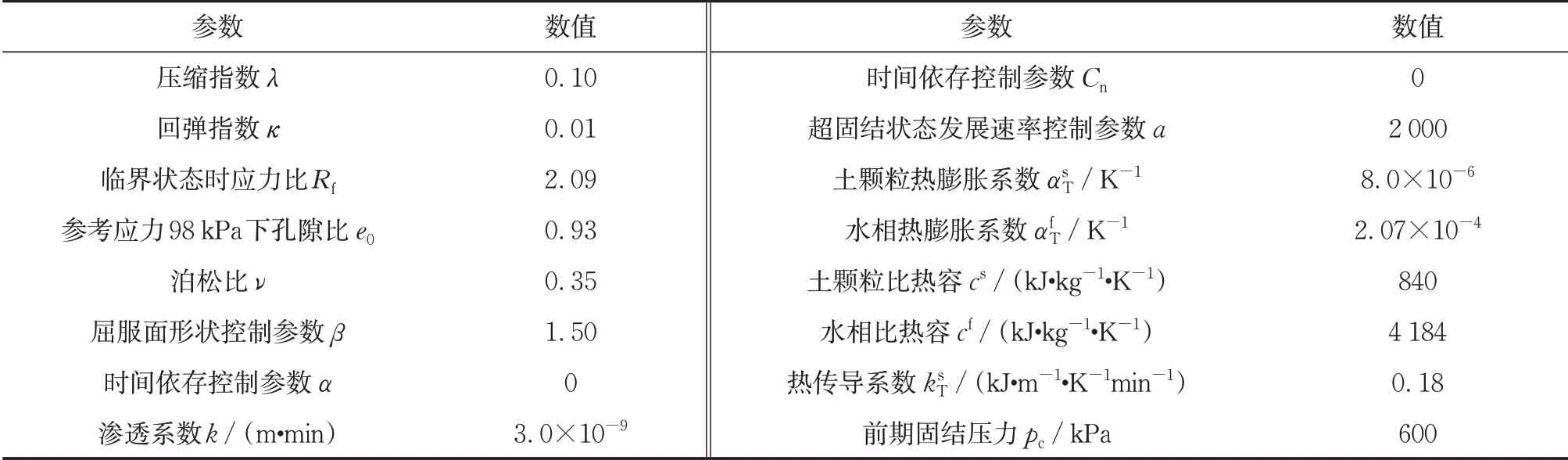
表1 模型参数及数值计算参数Tab.1 Parameters model and numerical analysis

图2为本文所采用的三维THM分析的有限元网格大小及其边界条件。模型中只对一个节点进行完全约束且确保在计算时模型不会在X与Y轴上发生旋转。与文献［6］中试验条件一样，模型中所有边界面设为排水边界面。计算时，试样初始温度设为22oC，以每小时4oC的升温速率进行加温，直到温度为90oC为止。

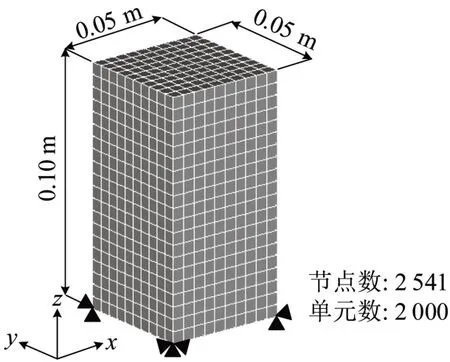
图2 有限元网格及边界条件Fig.2 Finite element mesh used in 3D analysis of heating tests and its boundary conditions

图3显示出了不同加温阶段时土体试样的温度分布。从图3中可发现，与文献［14］研究结果类似，即使模型尺寸缩小，试样内外部仍会存在一定的温度差，表明加热试验并非单元试验，而是一个边界值问题。

图3 不同加温阶段试样的温度分布Fig.3 Temperature distribution of testing sample in different heating stages

图4与图5分别给出了不同加温阶段试样的超孔隙水压与体积应变分布。从图4、5中可以清晰地发现，在加温时，试样内部会产生大小不等的超孔隙水压以及不均匀分布的体积应变。这些物理量的不均匀性进一步说明了加热试验并非单元试验，而是一个边界值问题。

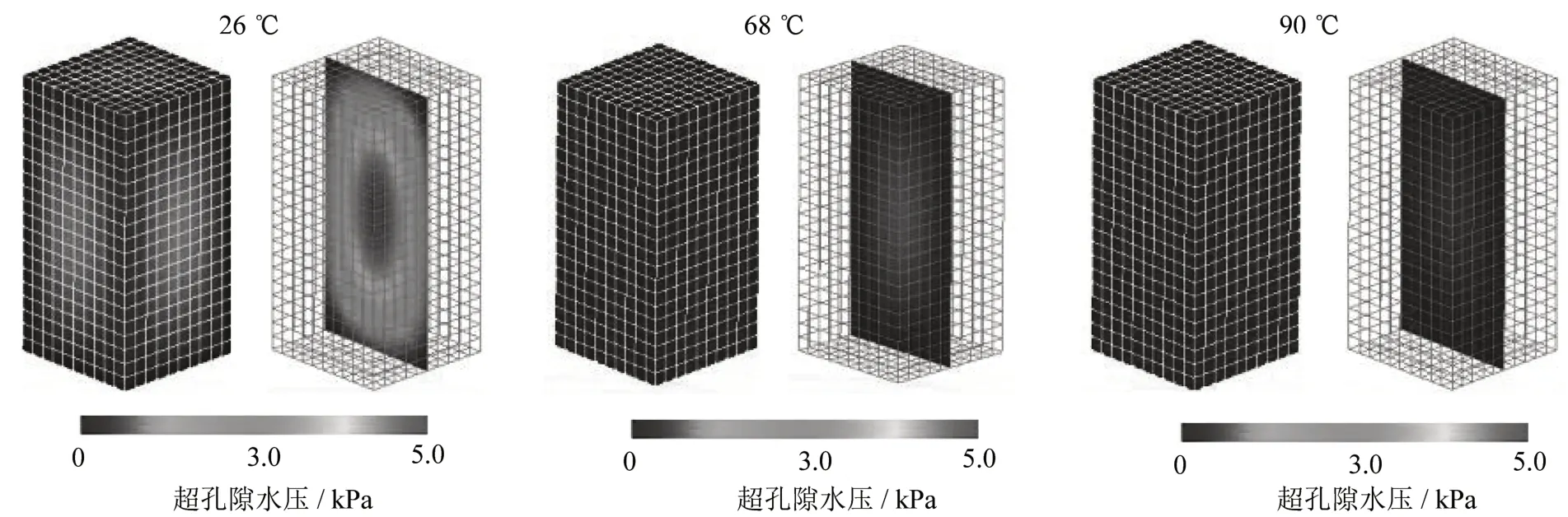
图4 不同加温阶段试样的超孔隙水压分布Fig.4 Excess pore water pressure distribution of testing sample in different heating stages

图5 不同加温阶段试样的体积应变分布Fig.5 Volumetric strain distribution of testing sample in different heating stages

图6给出了THM分析计算的温度与体积应变的关系。这里的体积应变是计算模型中所有2 000个单元的体积应变总和的平均值。由图6可知，当温度升高时，试样的体积变形表现为热压缩，这与文献［6］试验结果相吻合，尽管数值仍有一些差别。

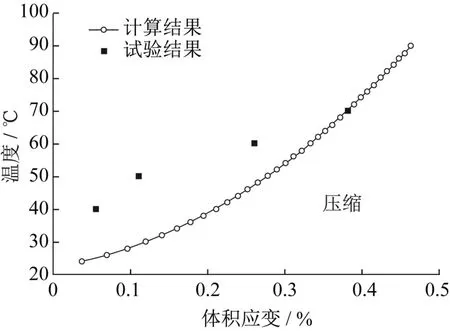
图6 温度与体积应变的关系Fig.6 Temperature versus volumetric strain

产生上述热压缩现象的原因是在升温过程中同时存在两个阶段：①热传导；②超孔隙水压消散。由于黏土的热传导系数远大于它的渗透系数，相对于超孔隙水压消散，热传导所需时间很少。故升温引起的黏土膨胀将会发生得非常快，紧随其后的是超孔隙水压力的缓慢消散，如图7所示。因此，基于本文数值分析结果可知，饱和固结黏土的加热试验产生的热压缩现象是由于升温过程中，土体内会产生一定的温度差，进而引起土体内部超孔隙水压的产生。随着时间增加，超孔隙水压逐渐消散，最终导致土体产生压缩。

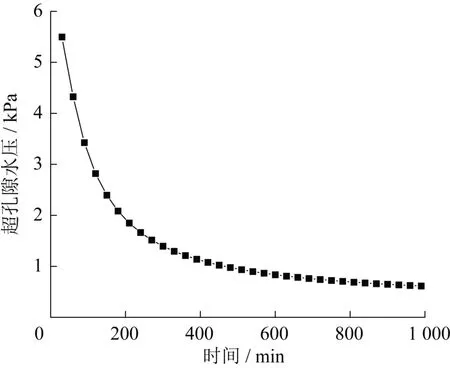
图7 计算模型中心单元超孔隙水压时程曲线Fig.7 Time history of excess pore water pressure of center element

为了进一步验证土体渗透系数在升温过程中对超孔隙水压的影响，将上述数值分析中采用的渗透系数增大100倍，其他参数不改变进行计算，如图8所示。

图8 不同加温阶段试样的超孔隙水压分布（渗透系数增大100倍）Fig.8 Excess pore water pressure distribution of testing sample in different heating stages (at an increased permeability coefficient of 100 times)

图9给出了不同加温阶段试样的体积应变分布。由图9可知，此时土体内外部的体积应变都表现为膨胀（计算中以压为正）。

从图10中可以很清晰地发现，与初始计算结果相反，随着温度的升高，土体的体积几乎呈线性膨胀。也就是说，在室内试验中发现的热压缩现象不是土体的固有属性，土体在受热时也遵循膨胀这一普遍规律。

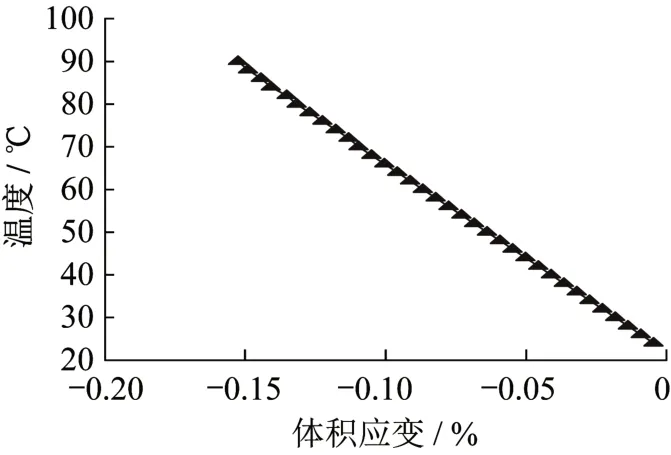
图10 温度与体积应变的关系（渗透系数增大100倍）Fig.10 Temperature versus volumetric strain (at an increased permeability coefficient of 100 times)

3 结论

本文基于一个能够描述温度对岩土材料变形和强度的影响，并考虑中间主应力的影响的热弹黏塑性模型，采用THM耦合有限元程序对室内饱和正常固结黏土加热试验进行了数值模拟。计算结果表明，室内加热试验不是单元试验，土体内部会产生不均匀的应力、应变和温度场。试验中产生的加热压缩现象是由于温度差产生的超孔隙水压消散而引发的，并非岩土材料的本质属性。当土体的渗透系数增大，温度差不会导致土体内部积累超孔隙水压，当土体升温时，则表现为热膨胀。也就是说土体在受热时也遵循膨胀这一普遍规律，而不必在构建热弹塑性模型时引入额外的参数来描述“软黏土因受热而体积收缩”这一现象。本文的研究结果能够为土体热力学行为的模拟提供有益的参考。

作者贡献声明：

张 锋：文章整体思路制定，修改论文。

熊勇林：论文初稿撰写。