预制复合墙板承载性能试验研究

高舒羽， 郭小农， 刘 青， 王宝林， 王玉波

（1.同济大学 土木工程学院，上海200092；2.上海同济绿建土建结构预制装配化工程技术有限公司，上海 200092；3.吉林恒源建设有限公司，吉林 吉林 130011）

随着预制装配式建筑的广泛应用，国内外对预制墙板的改进和研发力度也随之增大。新型预制墙板逐渐向减小自重、改善承载和抗震性能、增强保温节能效果、优化施工和降低成本等方面发展。近年来，国内外新型预制墙板的种类逐渐增多，针对墙板受力性能的研究也在同步展开。天津大学等研发出“CS板建筑体系”［1］，通过试验研究了CS （concrete sandwich） 板的抗剪性能，并提出其抗剪极限承载力的计算公式。Liu等［2-3］引进并改进了澳大利亚的速成墙板，研究了不同形式的灌芯纤维石膏墙板在低周反复荷载作用下的抗剪性能、变形能力和破坏特征等。西安建筑科技大学研发出密肋复合墙板［4］，探讨了墙体在水平低周反复荷载作用下的承载能力、延性、耗能等抗震性能，并提出了墙体的恢复力模型。为提高预制混凝土夹芯墙板的保温性能，Lameiras等［5］研发出一种新型预制夹芯墙板，采用玻璃纤维作为抗剪连接件，同时内外叶板采用钢纤维自密实混凝土。

目前，预制混凝土夹芯板是使用较为普遍的预制墙板形式之一，这种墙板一般由内外两侧的预制混凝土板及中间的保温材料构成，两侧混凝土板则通过抗剪连接件形成整体结构。Salmon等［6-7］在1994年便提出了这种新型的预制混凝土夹芯板，同时对此新型墙板进行了大量试验研究以探讨合理的抗剪连接件形式。Li等［8-9］对12片预制钢丝网夹芯墙板进行了轴心受压试验，研究了墙板的破坏形态、承载性能和稳定性，并得出了其承载力和稳定性计算公式。此外，随着预制混凝土结构在地震区低层建筑中的广泛应用，预制墙板作为预制混凝土结构的重要组成部分，其抗震性能也逐渐成为学者们的研究重点。连星等［10-11］通过预制叠合板式剪力墙的低周反复荷载试验，系统分析了预制墙板的承载力、延性、滞回性能以及耗能能力等特性，并且提出了预制叠合板式剪力墙的斜截面抗剪承载力公式。对预制开洞叠合剪力墙进行抗震性能试验研究后，王滋军等［12］得到了试件的滞回曲线、骨架曲线、刚度退化曲线、延性性能和耗能能力等性能。研究表明，预制开洞叠合剪力墙的受力性能基本和普通钢筋混凝土开洞剪力墙相同，具有较好的抗震性能。

基于上述研究，本文提出一种新型预制复合墙板，该墙板的内外叶板均为钢丝网混凝土薄板，中间内嵌发泡水泥块作为保温材料，墙板各部分通过钢筋桁架网格连接成为整体。该墙板既可以单独用作承重构件，也可以作为围护构件使用，同时具有生产便捷、成本低廉、安装方便等优点，在装配式建筑中具有广阔的发展和应用空间。本文对该新型预制复合墙板进行了试验研究。

1 试验设计

1.1 试件设计

预制复合墙板大致可分为3种规格：内墙、外墙和开洞外墙，3种墙板的桁架钢筋布置如图1所示。其中开洞外墙（WQK组）会在洞口周围进行加强，并根据洞口位置对桁架钢筋间距进行调整。

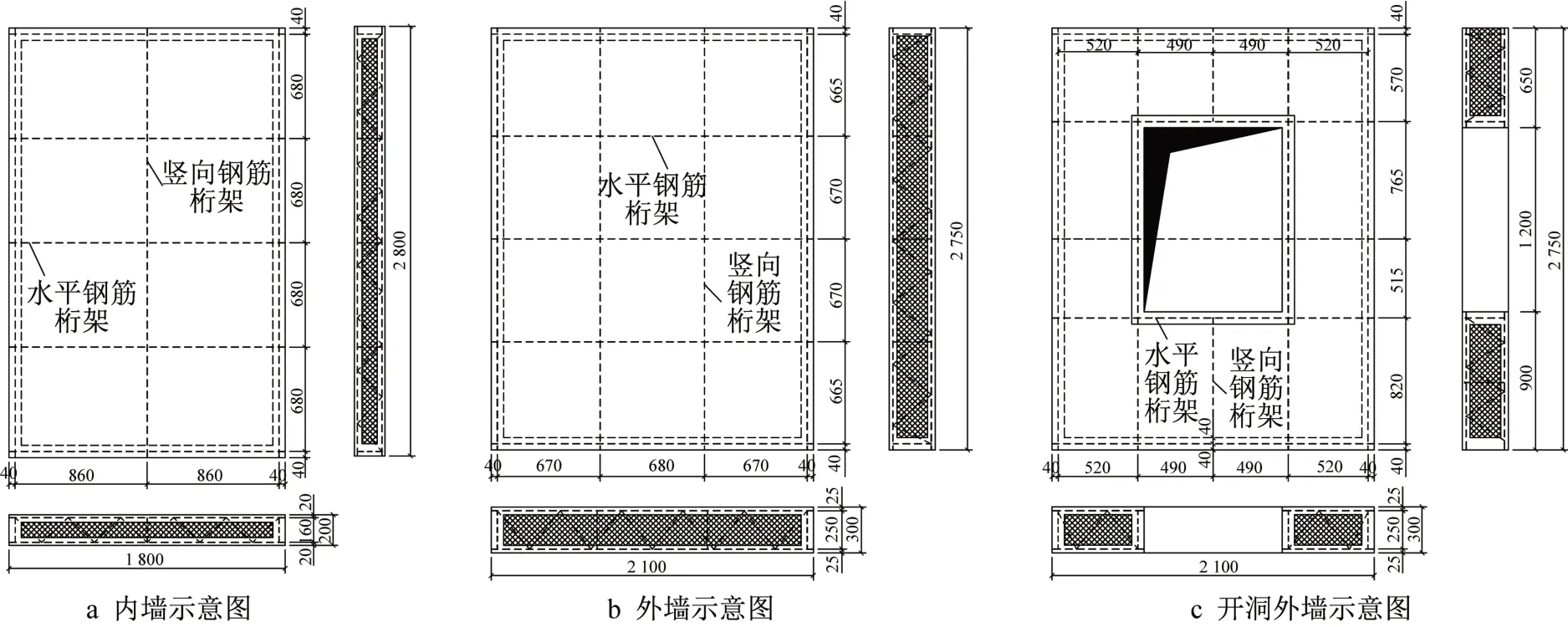
图1 预制复合墙板示意图（单位：mm）Fig.1 Prefabricated composite wall（unit：mm）

为推广预制复合墙板体系的使用，本文设计了3组共6个墙板试件，对不同规格墙板的抗侧性能进行了试验研究。试件内外板为钢丝网混凝土薄板，中间内嵌发泡水泥块体作为保温材料，墙体内部的纵横向钢筋桁架与钢丝网采用绑扎连接。此外，在墙板试件的顶部和底部分别增设了钢筋混凝土顶梁和底梁以方便加载和固定，如图2所示。各墙板试件的具体信息列于表1，内墙试件（NQ组）的厚度为200 mm，外墙（WQ组）和开洞外墙（WQK组）的厚度为300 mm，开洞外墙洞口底标高为0.9 m；内外钢丝网混凝土板的厚度均为40 mm，采用C30混凝土，并配有单层双向A2.5@100冷拔钢丝网；钢筋桁架的保护层厚为80 mm，桁架纵筋采用直径为8 mm的HRB400钢筋，桁架腹筋采用直径为6 mm的HPB300钢筋。

表1 试件信息表Tab.1 Main information of specimens

1.2 加载装置及方案

本试验在同济大学沪西校区的5 000 kN反力架上完成，主要探究3类墙板试件在一定轴压比下的抗侧性能，试验装置如图2所示。竖向千斤顶可以在反力架横梁上滑动，实现水平荷载的跟动，使得竖向荷载的位置相对于墙板试件不会发生变化；同时，分配梁使得竖向荷载均匀扩散到整个墙板上，水平连接件和拉杆可以实现水平荷载在试件顶梁处的往复循环加载；为避免墙板与反力架之间的相对滑移，在试件的工字形钢筋混凝土底梁处共设置了4个锚固钢架，以此形成端部固定边界条件；此外由于墙板平面外刚度较小，为了防止墙板在加载过程中发生平面外位移，在顶梁位置设置了侧向约束装置。

图2 加载装置图Fig.2 Loading device

试验采用力-位移双控制进行加载，首先在试件顶梁处施加恒定的竖向荷载，然后再施加水平荷载。鉴于墙体构造特点，对内墙施加轴心压力，对外墙施加偏心压力。每组共有2个试件，其中一个施加单调水平荷载以研究墙板的静力承载性能，另一个施加循环往复水平荷载以研究其滞回性能。在单调水平加载试验中，以每级20 kN的级差递增加载，每级荷载保持约60 s，观察数据采集仪记录的实时荷载-位移曲线，如发现曲线斜率有明显变化，则改用位移控制加载，直至试件破坏。在循环加载过程中，先单循环加载至屈服水平荷载Vy，然后按照0.5倍屈服位移δy为级差进行位移加载，每级循环3周。当试件承载力降低至峰值荷载的85%时，认为试件破坏，停止加载［13］。

1.3 测量方案

试验主要测量的内容有：墙板水平荷载、墙板水平位移、墙板表面混凝土和内部钢筋桁架的应变。所有试件的位移测点均按照图3进行布置，位移计D1和D2用来测量墙板顶部沿板宽方向的水平位移；D3和D4用来监测试件底梁相对于反力架是否发生滑动位移；D5、D7、D9和D11分别测试墙板顶部相对于地面的竖向位移；D6、D8、D10和D12则分别测试墙板底部4个角点相对于地面的竖向位移。

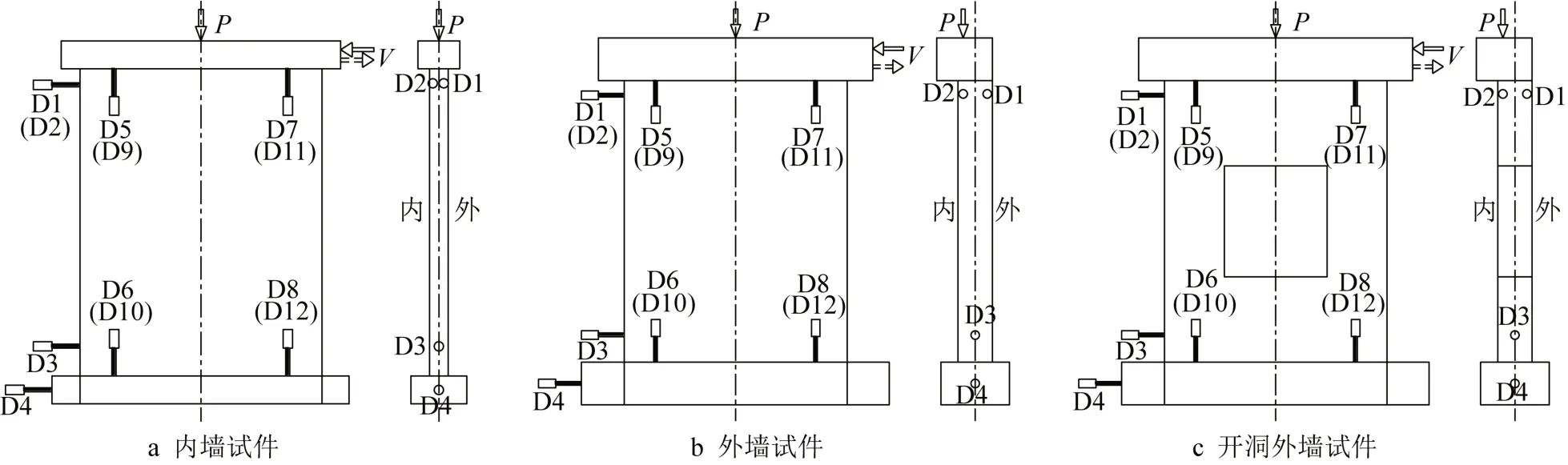
图3 位移测点布置示意图Fig.3 Layout of displacement measuring points

如图4所示，所有试件在墙板表面的混凝土及内部钢筋桁架均布置了位移测点。对于内墙和外墙试件，在墙板内外叶板表面混凝土上共对称布置10个竖向应变片（S1～S10）和8个横向应变片（SV1～SV8）；为了考察开洞对于墙板受力性能的影响，在开洞外墙的洞口附近又增设了应变片测点；同时，在墙板两侧竖向钢筋桁架底部的两肢纵筋处布置竖向应变片（C1～C4），测量加载过程中墙板内钢筋的应变发展情况。最后，在墙板表面画100 mm×100 mm方格网，方便记录试件裂缝的开展情况。

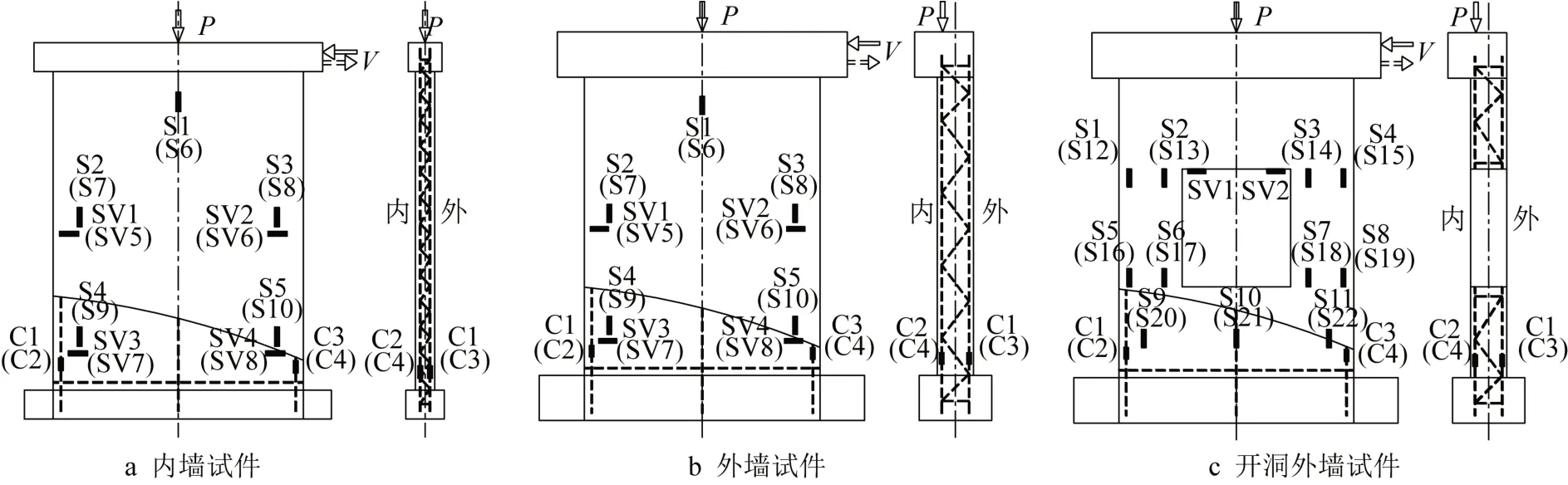
图4 应变测点布置示意图Fig.4 Layout of strain measuring points

2 试验结果及分析

2.1 材性试验

由于试验场地空间不足，试件分为2个批次进行浇筑：内墙（NQ组）为第1批次，外墙和开洞外墙（WQ组及WQK组）为第2批次。按照《普通混凝土力学性能试验方法标准》［14］，分别制作了标准立方体试块（150 mm×150 mm×150 mm）和标准棱柱体试块（150 mm×150 mm×300 mm），见图5。根据混凝土抗压强度和轴心抗压强度试验，得到了2个批次混凝土的抗压强度平均值和弹性模量平均值，如表2所示。然后，分别从同一批钢筋桁架和钢丝网中截取钢筋拉伸试件，根据国家标准《金属材料拉伸试验》［15］的规定，测得了钢筋和钢丝网的力学性能指标，见表2。由于钢筋和钢丝直径过小，试验过程中夹持端出现滑移，故未能测得其弹性模量。

表2 材性试验结果Tab.2 Material properties

图5 材性试验试件Fig.5 Specimens for material experiment

2.2 单调水平加载试验

2.2.1 试验现象

根据混凝土裂缝发展情况及荷载-墙顶位移曲线，试件的受力过程可划分成3个阶段：弹性阶段、弹塑性阶段及破坏阶段。在弹性阶段，荷载和位移两者基本呈线性增长关系，当到达开裂荷载Vcr时，墙板底部出现初始裂缝；在弹塑性阶段，荷载和位移继续增大，荷载-位移曲线出现一定的刚度退化，复合墙板的部分区域已经进入塑性阶段，墙板上裂缝的数量、长度及宽度也在不断增长；在破坏阶段，当达到峰值荷载Vmax后，曲线陡然下降，墙板受压侧混凝土压碎，受拉侧混凝土裂缝宽度增大，部分钢丝网拉断，试件迅速发生破坏，如图6所示。

图6 单调水平加载下试件破坏模式Fig.6 Failure modes of specimens at monotonic horizontal load

表3给出了墙板试件抗侧性能的相关参数。开裂荷载Vcr根据试验观察所得；由于单调水平加载试验试件的荷载-位移曲线没有明显的拐点，按照我国《建筑抗震试验规程》［13］的规定，试件的屈服荷载Vy和屈服位移δy按照能量等值法确定；试件的极限荷载Vu及极限位移δu分别对应荷载降至85%峰值荷载时的荷载和位移，若承载力未下降或下降未到85%，则取试验结束时为极限点。

表3 预制复合墙板抗侧性能Tab.3 Lateral performance of prefabricated composite walls

2.2.2 试验结果分析

图7a给出了单调水平加载下的各墙板不同高度处的荷载-位移（V - δ）曲线。结合图7和表3可知，随着墙板宽度及厚度的增加，墙板的刚度和承载能力有大幅度提升，但其延性有所下降。相比于内墙NQ-1，外墙WQ-1的峰值荷载提高了52.38%，但极限位移降低了22.95%。此外，洞口对墙体整体承载性能的影响较大，墙板开洞会极大提高其延性，但同时也会降低其承载力。相比于外墙WQ-1，开洞外墙的峰值荷载下降了35.38%，极限位移提高了89.97%。从图7b中可以看出，所有试件底梁的位移相对于墙顶位移较小，说明底梁固定牢靠，墙板和反力架之间的滑移可以忽略不计。

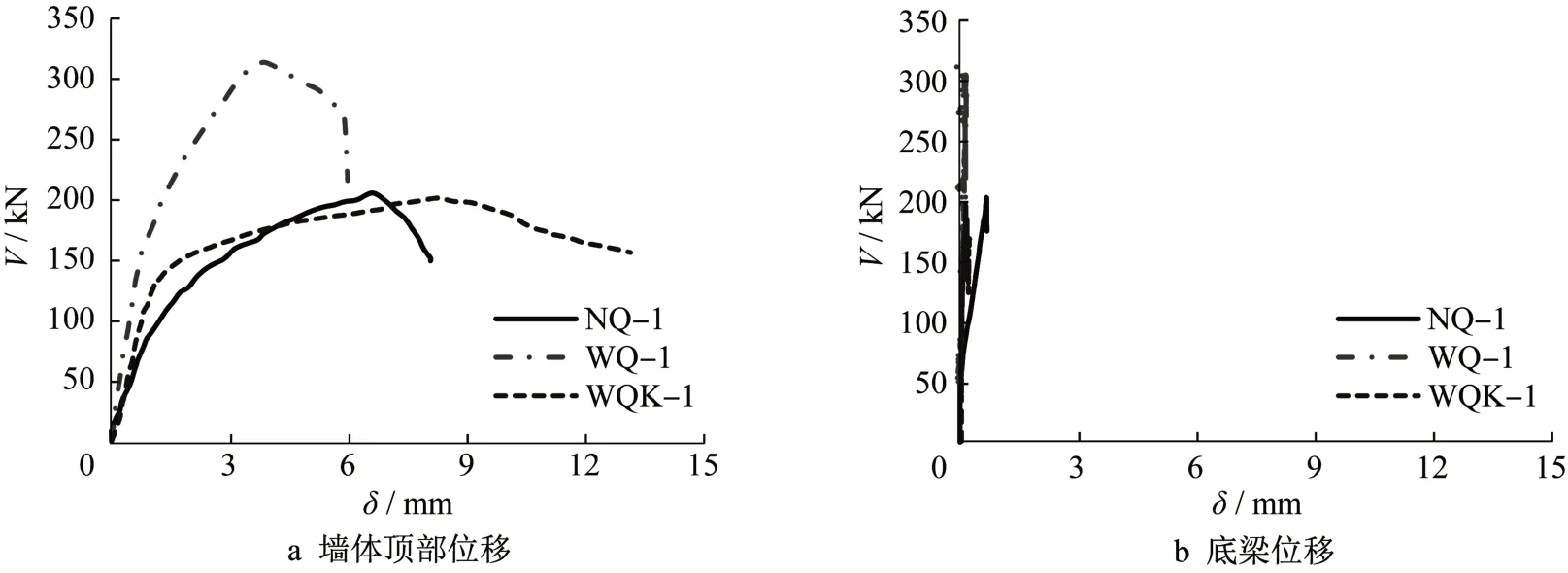
图7 荷载-位移曲线Fig.7 Curves of load-displacement

图8分别展示了外墙WQ-1的竖向桁架钢筋应变及混凝土应变在单调水平荷载下的变化规律。从图8a中可以看出，在加载初期，各钢筋应变ε与水平荷载V基本呈线性增长关系。随着荷载增大，荷载-应变曲线斜率发生明显变化。当荷载到达峰值后，受压侧钢筋（C1和C2）屈曲，受拉侧钢筋（C3和C4）也达到屈服。结合图4b和图8b可知，S4和S9应变片位于墙板受压侧，混凝土竖向应变始终为负值，且随着荷载的增大而逐渐增大。当水平荷载达到峰值荷载后，左侧混凝土受压破坏。S5和S10位于墙板受拉一侧，随着水平荷载增大，其受力状态由受压转变为受拉。当荷载达到约160 kN时，墙板受拉侧出现裂缝，混凝土应变超出应变片量程，应变片损坏。图中“●”表示该测点处应变片损坏，后续读数缺失或无效。

图8 外墙WQ-1荷载-应变曲线Fig.8 Curves of load-strain of specimen WQ-1

2.3 低周反复加载试验

2.3.1 试验现象

在加载初期，墙板底部在循环荷载的作用下出现了水平裂缝。随着荷载的增加，墙板持续发出开裂的声音，裂缝分布范围逐渐向墙板上部扩张，其数量逐渐增多，长度和宽度也随之增加。最终，受压区混凝土压碎，受拉钢丝网及钢筋达到屈服，墙板发生破坏。图9展示了部分试件的裂缝分布形式及混凝土压碎图状态。

图9 低周反复加载下试件破坏模式Fig.9 Failure modes of specimens at cyclic load

2.3.2 试验结果分析

2.3.2.1 滞回曲线及骨架曲线

各试件的滞回曲线及骨架曲线如图10和图11所示。与单调水平加载的情况类似，墙板在低周反复荷载作用下的受力过程也可分为弹性、弹塑性及破坏3个阶段。在弹性阶段，水平荷载和墙板位移呈线性增长关系，滞回环面积较小，刚度退化不明显，残余变形也较小。在弹塑性阶段，荷载-位移曲线出现一定的刚度退化，滞回环的面积也在逐渐增大，其形状由“梭形”变为“反S形”，荷载卸载到零时会出现明显的残余变形。最后达到破坏阶段，试件由于塑性损伤累积，强度和刚度退化较大，当达到峰值荷载后，曲线陡然下降，墙板底部混凝土压碎，钢筋达到屈服，部分钢丝网拉断，如图9所示。

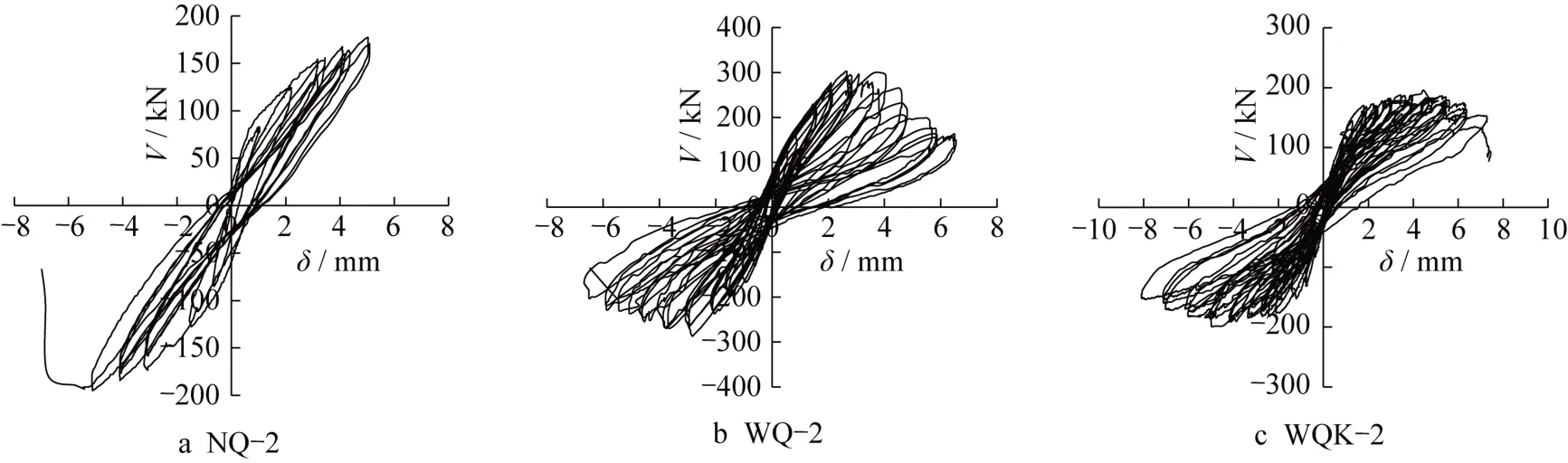
图10 墙板试件滞回曲线Fig.10 Hysteretic curves of specimens

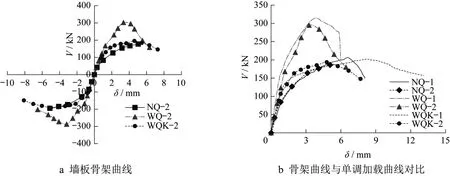
图11 骨架曲线对比Fig.11 Comparison curves of skeleton

图11a对比了3种墙板的骨架曲线。从图11a中可以看出：①外墙WQ-2的承载力最高。相比开洞外墙，其正向峰值荷载提高了54.87%，负向峰值荷载提高了49.56%；相比内墙试件，其正向和负向峰值荷载分别提高了70.53%和47.26%。②开洞外墙的延性最好。相比试件WQ-2，其正向极限位移从4.73 mm提高到6.50 mm，负向位移从-4.94 mm提高到-7.37 mm，由此可见，开洞会大幅度提高墙板的延性。③ 3种墙板的骨架曲线较为相似，三者初始刚度相差较小，但试件WQ-2刚度最大；当裂缝出现后，各墙板刚度开始下降，其中内墙NQ-2刚度的下降幅度最大。

由于试件正负向加载不对称，取正向荷载与位移绝对值的平均值绘制骨架曲线，并与单调水平加载的荷载-位移曲线进行对比，如图11b所示，可以看出，各类墙板的骨架曲线形状大体上和单调加载曲线相似。在加载前期，两条曲线接近于重合，初始刚度基本一致；在加载后期，墙板滞回曲线的强度和刚度有较为明显的退化，且极限位移降低。

结构或构件的变形能力一般用延性系数来定量表述，其计算公式如下：

式中：δu为极限位移；δy为屈服位移。

极限位移δu为承载力下降至峰值荷载85%时的墙板位移，若承载力未下降至85%的峰值荷载，则取试验结束时的墙体位移为极限位移；屈服位移δy按照能量等值法确定，如图12所示。

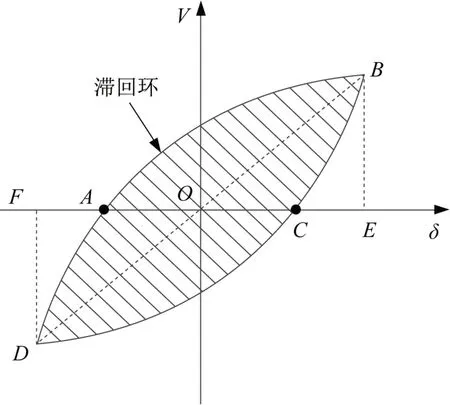
图12 能量耗散系数定义Fig.12 Determination of the energy dissipation factor

表4列出了根据式（1）计算得到的各墙板的延性系数及其他滞回性能参数。内墙NQ-2和外墙WQ-2的延性系数分别为1.78和1.91，开洞外墙的延性系数为3.10。由此可见，洞口可以大幅度提高墙板的延性。

表4 预制复合墙板滞回性能Tab.4 Hysteretic behavior of prefabricated composite walls

2.3.2.3 耗能能力

各年级学生退位减法和不退位减法在口算速度上的平均用时和标准差如表4所示，其中“1-1不退位”表示“一位数减一位数不退位减法”，“2-1不退位”表示“两位数减一位数的不退位减法”，“2-1退位”表示“两位数减一位数的退位减法”．

耗能能力是指结构或构件在地震作用下通过自身发生塑性变形而消耗地震能量的能力。低周反复荷载作用下，结构或构件荷载-位移曲线所包围的面积是衡量其耗能能力的重要指标。通常滞回曲线越饱满，滞回环包围的面积越大，耗散的能量越多，耗能能力越强。结构或构件的耗能能力常用能量耗散系数η来衡量。

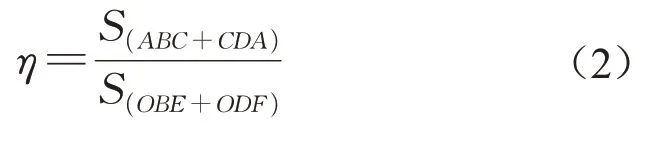
式中：S(ABC+CDA)为荷载-位移滞回环的面积；S(OBE+ODF)为滞回环卸载段与横坐标轴围成的三角形面积，如图12所示。

图13对比了不同墙板的能量耗散系数随荷载等级N的变化。总体来说，各类墙板的耗能系数随荷载等级增加呈上升趋势。内墙的滞回次数明显低于外墙和开洞外墙，加载到第6级，试件便发生破坏。开洞外墙WQK-2的耗能能力明显优于普通外墙WQ-2，洞口可有效提高墙板的耗能能力。

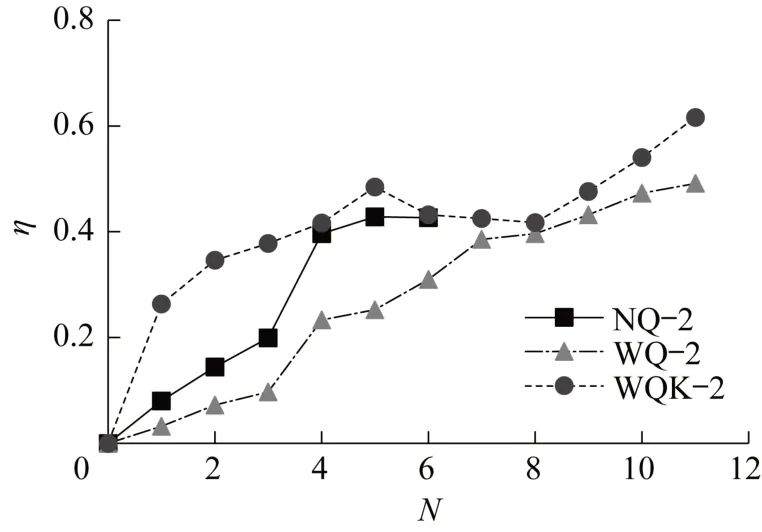
图13 能量耗散系数随荷载等级的变化Fig.13 Energy dissipation factor versus load level

3 数值模拟

通过上文分析可知，墙板的骨架曲线与单调水平加载曲线较为近似，为节省计算时间，本文仅对单调水平加载下的墙板试件进行有限元分析。采用ABAQUS建立了与试验试件相同尺寸的有限元模型，模型中各部件及组装图如图14所示。试件底梁的主要作用使墙板与反力架之间不发生相对位移，以此模拟复合墙板的端部固支边界条件。为节省计算成本和时间，数值模型中不建立底梁部件，直接在墙板底部施加固定约束。同时，由于水平桁架与竖向桁架采用等强焊接，两者采用一个整体桁架钢筋笼来模拟。在模型中，采用实体单元C3D8R模拟空腔混凝土板和顶梁，采用桁架单元T3D2模拟桁架钢筋笼和钢丝网。此外，钢筋和混凝土的本构关系分别采用双折线随动强化模型和塑性损伤模型，各部件的力学性能指标根据材性试验实测结果确定。

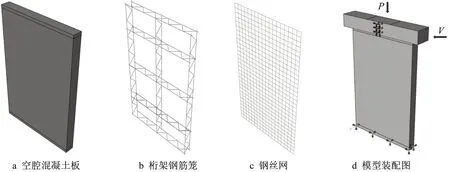
图14 有限元模型Fig.14 Comparison curves of skeleton

图15给出了试件WQ-1的试验破坏照片和有限元分析应力云图。从应力云图可知，空腔混凝土板受压侧应力最大，大片钢丝网及钢筋桁架已经达到屈服应力，对应了试验所得到的破坏模式：受压侧混凝土压碎，受拉侧部分钢丝网拉断，钢筋桁架达到屈服。对比可知，有限元模型的破坏模式与试验得到的破坏模式基本吻合。图16将墙板水平加载数值模型的荷载-位移曲线与试验实测曲线进行对比。以外墙墙板试件为例，WQ-1的荷载-位移曲线、 WQ-2的荷载-位移骨架曲线与有限元所得荷载-位移曲线较为吻合。有限元所得的墙板峰值荷载为309.98 kN，与WQ-1进行比较，极限承载力误差仅为1.33%。综上所述，该有限元模型可以较好地模拟墙板的真实受力情况，为墙板承载性能的深入研究提供了有力依据。

图15 破坏模式对比Fig.15 Failure mode of specimen WQ-1

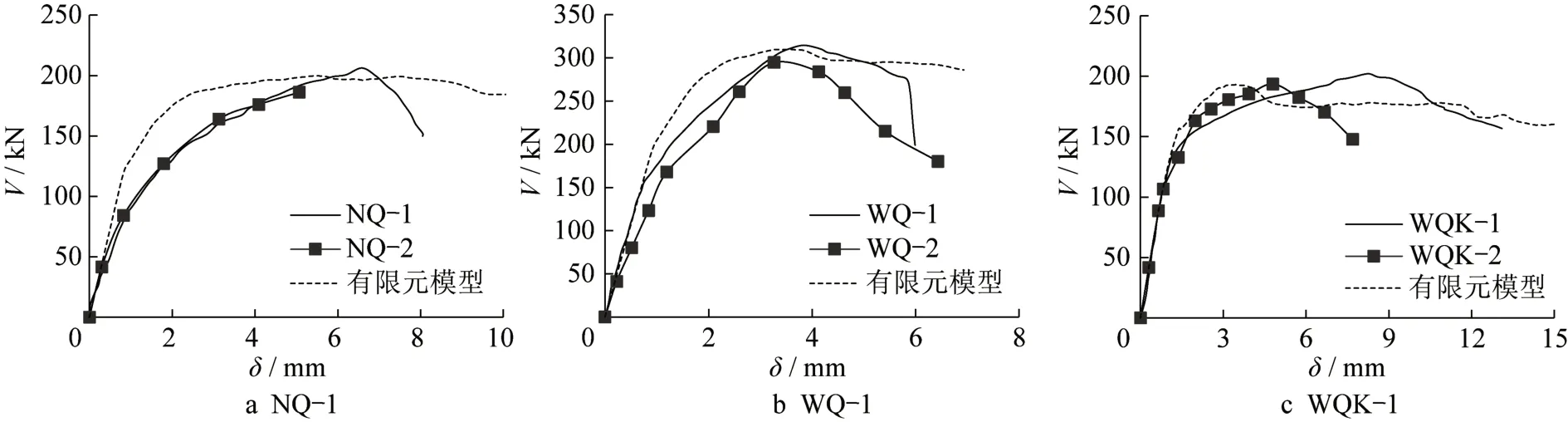
图16 试件荷载-位移曲线对比Fig.16 Load-displacement curves of specimens

4 结论

本文提出了一种新型预制复合墙板，并对内墙、外墙和开洞外墙共3种规格的墙板分别进行了单调水平加载试验和低周反复加载试验，通过试验结果可得出如下结论：

（1）试件在单调水平荷载和低周反复荷载作用下的破坏模式均为混凝土压碎、部分钢筋桁架和钢丝网受拉屈服。

（2）墙板在单调水平加载下的峰值荷载分别为206.16、314.15和201.99 kN，此预制复合墙板具有良好的承载能力。

（3）墙板的骨架曲线与单调水平加载的荷载-位移曲线较为相似，墙板具有良好的延性和耗能能力；墙板开洞可有效提高其变形能力和耗能能力，同时也会大幅降低其极限承载力。

（4）有限元分析与试验的对比结果表明，本文所建立的有限元模型可以较好地模拟墙板的破坏模式和受力状态，为墙板承载性能的深入研究提供了有力依据。

作者贡献声明：

高舒羽：模型构建，数据分析，论文写作。

郭小农：论文构思，论文修改。

刘 青：资金支持，提供试验意见。

王宝林：资金支持，提供试验意见。

王玉波：资金支持，提供试验意见。