Si3N4陶瓷球研磨轨迹分析及其对表面质量的影响机制

孙健，陈伟，姚金梅，李颂华,b，田军兴,b

Si3N4陶瓷球研磨轨迹分析及其对表面质量的影响机制

孙健a，陈伟a，姚金梅a，李颂华a,b，田军兴a,b

（沈阳建筑大学 a.机械工程学院 b.高档石材数控加工装备与技术国家地方联合工程实验室，沈阳 110168）

明确在相同的研磨液配比、磨料类型，不同的研磨盘转速、研磨装置施加的载荷、磨粒粒径下，陶瓷球研磨轨迹对陶瓷球表面质量的影响，确定锥形研磨法加工的氮化硅陶瓷球的最优研磨参数，提高陶瓷球的表面质量。首先建立研磨盘和氮化硅陶瓷球的相对运动模型，利用MATLAB模拟不同研磨参数的下氮化硅陶瓷球的研磨轨迹，分析得到研磨参数和研磨轨迹的变化关系；再利用锥形研磨装置进行单因素实验验证，参与实验的3个变量设定为磨粒型号（粒径）、研磨盘转速和研磨装置施加载荷，将实验结果取样，通过粗糙度仪测量球体的表面粗糙度，用扫描电镜和超景深三维显微镜检测研磨后的陶瓷球表面形貌，结合仿真分析和实验结果探究研磨参数对加工后表面质量的影响。将不同仿真轨迹下得到的研磨参数变化规律与实验结果相结合，得到了最佳的研磨参数，即研磨盘转速为50 r/min，施加的载荷为1.30 N，磨粒类型为W7。在此条件下得到的陶瓷球表面的粗糙度为0.009 6 μm，基本能达到实际生产中对G3级精度全陶瓷球的质量要求。陶瓷球的表面质量受到研磨盘转速、研磨装置施加载荷及磨粒粒径的影响较大，由仿真分析和实验结合可知，在研磨过程中随着磨粒粒径的减小，以及研磨盘转速和载荷的下降，陶瓷球的研磨轨迹趋于稀疏，表面粗糙度呈下降趋势。研磨氮化硅陶瓷球时取粒径较小的磨粒，以较低的研磨盘转速和较小的研磨装置施加载荷有利于提高其表面质量。此研究成果对提高陶瓷球的表面质量具有重要的指导意义。

氮化硅陶瓷球；锥形研磨法；研磨参数；研磨轨迹；单因素实验；表面质量

陶瓷球轴承作为陶瓷材料的新型轴承产品在多个工业领域有着显著的作用和广阔的使用前景。相对于普通碳钢轴承，陶瓷球轴承具有强度高、硬度高、膨胀系数低、耐腐蚀、耐磨损等优点，且具有在极端复杂工况下正常运行的能力[1-3]，在当今的高端产品设计和开发有着不可或缺的地位，这体现在航空航天相关设备、精密机械仪器及国防军事制造等领域。随着陶瓷球轴承在我国高端制造产业和高精尖行业中的应用对其性能也提出了更高的要求。陶瓷球作为陶瓷球轴承的关键组件，其表面质量对陶瓷球轴承的使用性能、工艺性能等具有重要的意义[4-6]。

为了提高陶瓷球在研磨过程中的表面质量，国内外部分学者对此进行了深入的研究。Baraheni等[7]基于传统V形槽研磨装置，在研磨盘上增加了1圈游动沟槽，有效地降低了其表面粗糙度，但是该方法的加工效率偏低，且加工得到的成品球的表面质量较差。周芬芬等[8]基于阿基米德螺线提出了一种能够使陶瓷球在沟槽上的曲率半径保持连续变化的方法，该方法能较好地控制研磨过程中的压力和速度，加工后得到的球体的表面粗糙度接近5 nm，但是这种研磨方式对沟槽曲率加工的要求较高，且装置设计较为复杂，不便于大规模化使用。张珂等[9-10]通过对氮化硅陶瓷球进行研磨实验，探讨了不同材料去除方式对加工表面质量的影响，发现在二体断裂去除方式下其表面粗糙度较差。Kumar等[11]基于磁流体在磁场的作用提出了磁流体研磨加工方法，周芬芬教授等[12]验证了采用该方法生产的成品球的表面粗糙度趋近20 nm。在此基础上，Zhang等[13-14]通过实验发现，改变上下研磨盘轴线的偏移量能够很好地提高研磨效率和表面质量，降低球形误差，但是此类方法的造价较为昂贵，对于现阶段推广来说存在较大的阻碍。沈阳建筑大学的吴玉厚教授团队[15-18]对氮化硅陶瓷球的研磨进行了深入的研究，提出了研磨工艺参数对表面粗糙度的影响。浙江工业大学袁巨龙教授团队[19]通过调节研磨盘的转速控制研磨过程中的轨迹，提出了双自转的加工方法，这种方法虽然提高了加工质量，但其控制过程较复杂，仅适用于小批量加工。浙江工业大学王旭等[20]在日本金泽大学黑布利次教授的研究基础上，通过将传统的V形槽研磨装置下的研磨盘进行转速分层，提出了自转角主动控制方法，这种方法能够极大地提高表面质量，但是其分层后产生的附加装置过多，不适于工业化大批量生产。

综上所述，现存的几种主流陶瓷球研磨方式在球体研磨成型方面都存在不足，对陶瓷球研磨轨迹的分析及不同轨迹下研磨参数与表面质量之间的关系缺乏有效的实验数据支撑。基于此，文中以氮化硅陶瓷球为研究对象，通过MATLAB对研磨轨迹进行仿真，使用锥形研磨装置进行研磨加工，对陶瓷球的表面研磨机理进行分析，将仿真结果与实验结果相结合，分析不同参数下的研磨轨迹对表面粗糙度和微观形貌的影响。

1 锥形研磨盘下的陶瓷球运动状态分析及仿真模型的建立

1.1 陶瓷球在研磨盘中的静力学分析

氮化硅陶瓷球在锥形研磨加工过程中的状态如图1a所示，通常会受到多种因素的影响，包括研磨盘转速、载荷、研磨液等[21]。这里对氮化硅陶瓷球研磨过程进行如下假设：上下研磨盘和陶瓷球为理想刚体；陶瓷球为直径相等的理想球体，同时球体之间未发生相互作用；锥形槽与球为理想三点接触；陶瓷球沿研磨方向无相对滑动；不考虑研磨过程中研磨液的影响。基于上述条件，建立氮化硅陶瓷球在锥形槽研磨过程中的简化形式，受力分析如图1b所示。

定义球体的质量为，研磨装置施加在单颗陶瓷球上的载荷为N，研磨盘的锥形角为，载荷N沿着锥形槽边缘的分力为A，见式（1）。

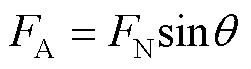
分析可知，N作用在锥形槽边沿上的分力起到了驱动陶瓷球做研磨运动的作用。将此力沿着水平方向进行分解，得到驱动球体转动的力A，见式（2）。

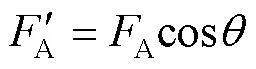
将式（1）与式（2）合并，可以得到A，见式（3）。

可得上研磨盘施加的载荷N作用在陶瓷球上力产生的速度1，见式（4）。

陶瓷球绕着研磨盘在锥形槽接触3个点形成的转动半径分别为ABC。将锥形研磨盘的下研磨盘固定，研磨盘的转速设定为g，设定在理想研磨加工环境下陶瓷球的半径不变，陶瓷球在锥形槽内自转的角速度为Z，陶瓷球的公转的角速度为p，陶瓷球的自转角为，陶瓷球在研磨加工过程中的平衡方程组见式（5）—（6）[22]。

(5)

(6)

(7)

上面这组公式中，接触点和接触点的转动半径的计算见式（8）—（9）。

(9)

将转动半径的公式带入陶瓷球的运动平衡方程，然后进行求解，可得自旋角、公转角速度p、陶瓷球的自转角速度z，平衡方程见式（10）—（12）。

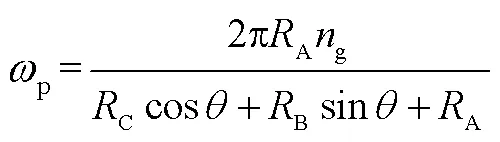
从计算结果分析可知，现有实验装置对陶瓷球自转角的改变较小，有的甚至不发生变化。基于此，考虑将陶瓷球的自转角设为常量。在研磨过程中，公转角速度和陶瓷球的自转角速度完全取决于实验装置本身的条件，例如研磨盘外部驱动速度和研磨盘的尺寸等。在保持这些量不变的前提下，公转角速度和自转角速度也不会发生变动。

在研磨陶瓷球球体时使用的同一批次磨料中，磨粒的形状和尺寸存在较大的差异。这是由于磨料本身就是磨粒晶体通过制粒破碎的方式生成的，且磨料在加工过程中与球体之间的相互作用致使单颗磨粒发生了破碎和断裂。从简化模型和提高计算效率的角度出发，将磨粒的几何特性抽象化，以逼近磨粒的实际形状，常见的形状如图2所示，主要有球体、锥体、多棱锥体等。其中，多棱锥体最接近磨粒的实际尺寸[23]。

图2 常见的磨粒形状

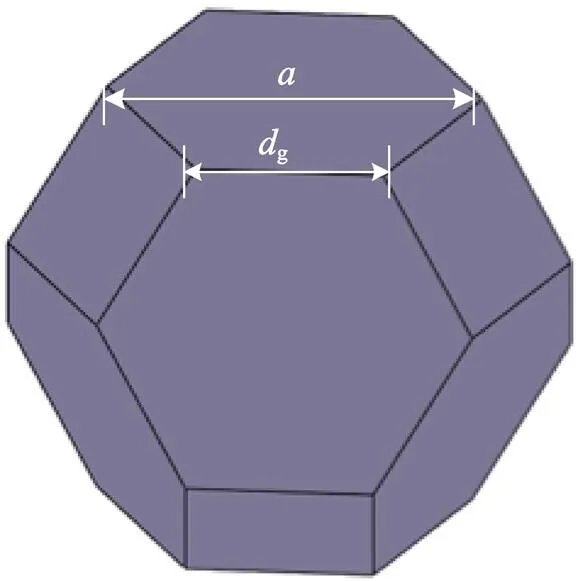
图3 金刚石磨粒

在确定磨料类型的情况下，考虑磨粒的粒径g在研磨过程中对球体转动的影响，设定研磨过程中单颗磨粒受到的力为N，磨粒的数量为，磨粒的硬度为p，陶瓷球的硬度为b，研磨过程中单颗磨粒与球体的接触面积为。建立磨粒对球体表面的作用模型如图4所示。

图4 磨粒对球体作用简图

其中，为磨粒压入工件表面部分的夹角半角，D为材料的动态维氏硬度，见式（13）。

0为压痕区域的半径，压痕深度表示为Pg/b。在切削过程中0的变化范围为g到，且0与的关系见式（14），其中系数为0.43[24]。

在研磨过程中，磨粒作用在球体表面产生的压力见式（15）。

为磨粒作用在陶瓷球表面所产生的动能，计算见式（16）。

(16)

假设研磨过程中磨粒在球体表面为无弹性碰撞，且磨粒作用产生的动能可全部转化为材料表面的变形能。此时磨粒作用在球体表面所产生的最大载荷L的计算见式（17）。

载荷L在研磨过程对球体中所产生的速度2见式（18）。

上述公式的建立说明，在研磨过程中磨粒的尺寸对于球体的转动有着重要的影响，在相同工况下，改变磨粒的粒径g，则压痕深度和压痕区域的半径0也会随之变化。这些要素的改变直接导致磨粒作用产生的动能发生变化，磨粒作用产生的最大载荷改变，最终对球体的运动状态产生影响。

1.2 研磨盘与陶瓷球的运动学分析

现设定氮化硅陶瓷球的公转角速度和自转角速度分别为p和z。将相对运动分析的原点设定在研磨盘的回转中心p，以此建立静坐标系，即陶瓷球公转坐标系[p，1，1]，将相对运动分析的原点设定在陶瓷球的回转中心g，建立与之对应的动坐标系[25-26]，即陶瓷球自转坐标系[p，2，2]。研磨盘和陶瓷球的相对运动学模型如图5所示，该模型中陶瓷球在研磨过程中的初始相位角为，设定研磨滚道上陶瓷球任一点相对于研磨盘作匀速圆周运动，将点到p的径向距离设定为，研磨盘的回转中心p到球的回转中心g的距离设定为陶瓷球的研磨轨迹可以表示为其相对于研磨盘的运动轨迹。

图5 陶瓷球研磨过程中的运动学分析

从图5可知，陶瓷球上任意一点的坐标为（q，q），已知点相对于以研磨盘中点p为坐标原点的静坐标系[p，1，1]做匀速圆周运动，可以得到点的运动方程，见式（19）—（20）。

(20)

由此得到和磨粒运动方程式是建立在以研磨盘的回转中心p为原点的静坐标系[p，1，1]下的。考虑如何将此运动方程表示在以陶瓷球的回转中心g为原点的动坐标系[p，2，2]中。

由矩阵的基本知识可知，运动方程只要乘以对应的矩阵就能实现坐标的旋转和平移变换。将静坐标系下的运动方程转化为动坐标系下的运动方程，具体步骤如下。

先对点的坐标进行平移变换，见式（21）。再对坐标系进行旋转变换，见式（22）。

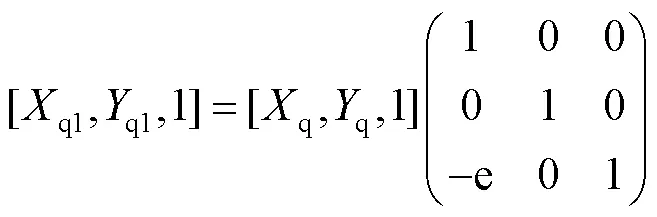
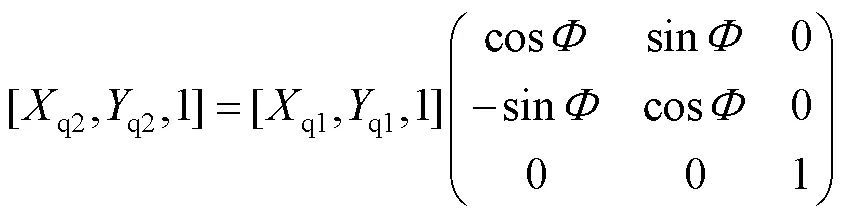
综上可知，公转坐标系相对于陶瓷球中心坐标系下的转变方程可以表示为式（23）。

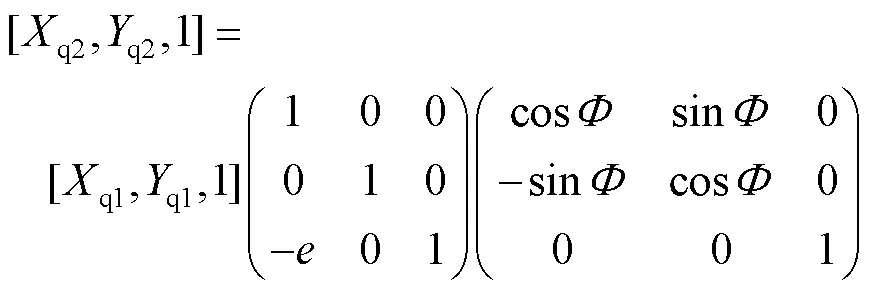
由于陶瓷球在自转时会产生自旋角度，基于此，需要将中心坐标系表示在陶瓷球自传坐标系中，即将陶瓷球中心坐标系乘以一个对应的变换矩阵Rot（）。其中，设陶瓷球自旋角为，则坐标转换见式（24）。

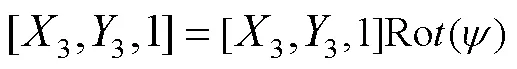
将陶瓷球的运动方程用此方法进行转换，并将磨粒和载荷作用下产生的速度分别带入，可以得到陶瓷球在研磨盘上的相对运动方程，从而建立陶瓷球研磨轨迹的数学模型，见式（25）—（26）。

(25)

(26)

从陶瓷球的运动轨迹模型可知，在球体质量、初始相位角中心距等因素确定的情况下球体在研磨过程中的运动状态与陶瓷球公转/自转角速度p和z，研磨装置施加在单颗陶瓷球上的压力N，以及磨粒粒径g的相关性较大。由式（7）可知，在研磨盘尺寸不变的条件下，p和z由研磨盘转速g决定。上述分析为后续仿真的展开打下了坚实的理论基础。

2 基于锥形研磨法的氮化硅陶瓷球研磨轨迹仿真分析

2.1 仿真条件

陶瓷球研磨轨迹方程的主要影响参数为研磨盘转速g、单颗陶瓷球所受载荷N、磨粒尺寸。由于文中主要研究转速、载荷、磨粒尺寸对研磨轨迹的影响，所以将自旋角设为常量。

基于上述条件，此次仿真设定锥形研磨装置的上、下研磨盘直径p均为320 mm，氮化硅陶瓷球的初始毛坯球直径=10 mm；取磨粒的型号为W7到W30；下研磨盘锥形槽的槽角=45°，陶瓷球旋转中心到下研磨盘中点的距离=150 mm；被加工陶瓷球的质量=350 mg。研磨盘的转速的变化范围为50～200 r/min，陶瓷球的自旋角固定为45°左右，研磨装置施加的载荷范围为1.30～8.67 N，仿真时间为100 s，采样步长为0.01。

2.2 仿真及其结果分析

利用MATLAB模拟锥形研磨盘研磨氮化硅陶瓷球时的轨迹，根据研磨参数分成3组，并进行仿真分析。

第1组仿真设定研磨盘的转速g为自变量，分别取4组转速（50、100、150、200 r/min）为实验对象。经分析可知，当研磨过程中的自转角= 45°、施加载荷N=1.30 N、磨粒的型号为W7时，分别改变研磨盘的转速，得到的仿真研磨轨迹如图6所示。

由图6得出，在研磨装置的转速为50 r/min时，陶瓷球的研磨轨迹较为凌乱，呈稀疏状。将转速增至100 r/min时，陶瓷球的研磨轨迹开始变得密集，多条研磨轨迹相互交错。继续将转速增至150 r/min，陶瓷球的研磨轨迹变得更加密集。当转速达到200 r/min时，陶瓷球研磨轨迹的密集程度趋于顶峰。说明随着转速的增加，陶瓷球研磨轨迹的密集程度得到提升。该现象出现的原因是转速的增大，在单位时间内参与研磨的陶瓷球数量增加，则研磨过程中产生的轨迹变得密集。

第2组仿真设定施加载荷为自变量，分别取4组载荷（1.30、4.33、6.33、8.67 N）为实验对象。经分析可知，当研磨过程中的转速g=50 r/min、自转角=45°、磨粒的型号为W7时，分别改变研磨盘的载荷，得到的仿真研磨轨迹如图7所示。

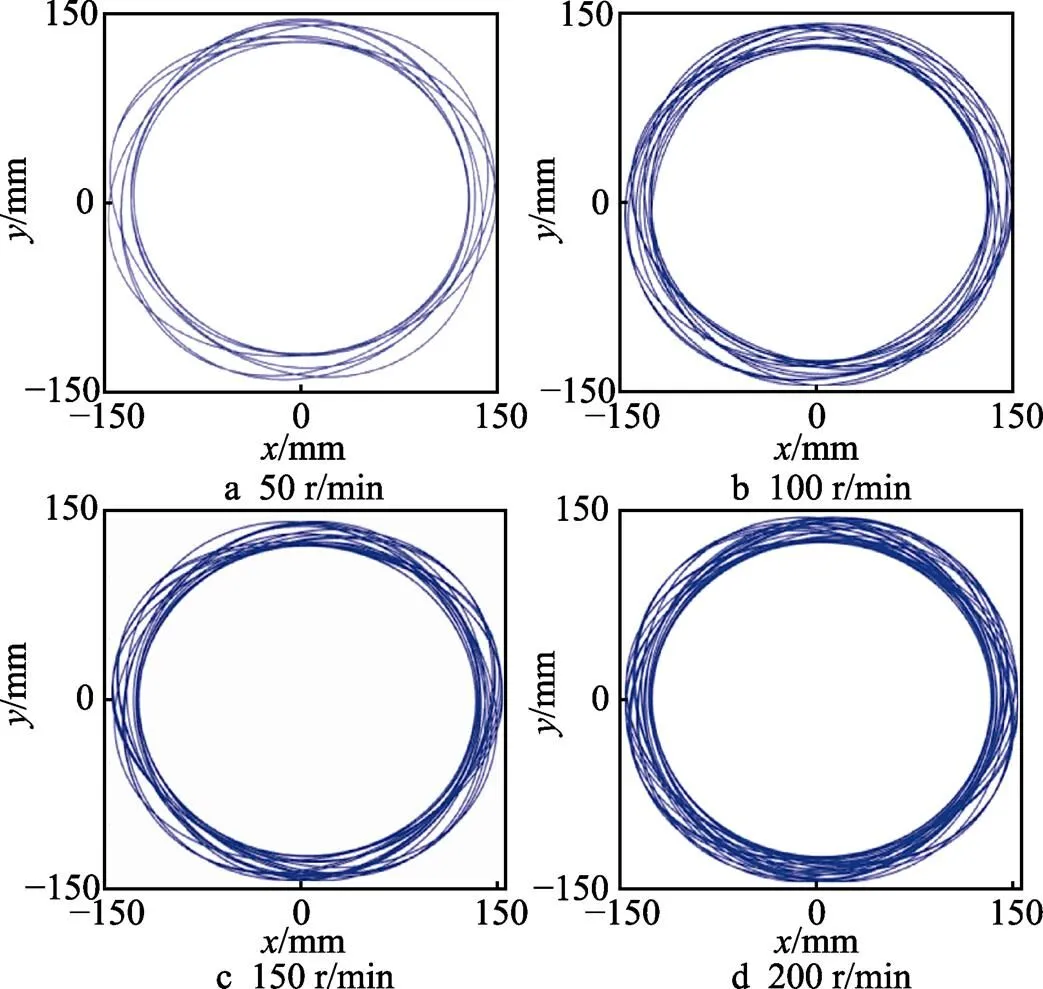
图6 改变研磨装置转速的研磨轨迹

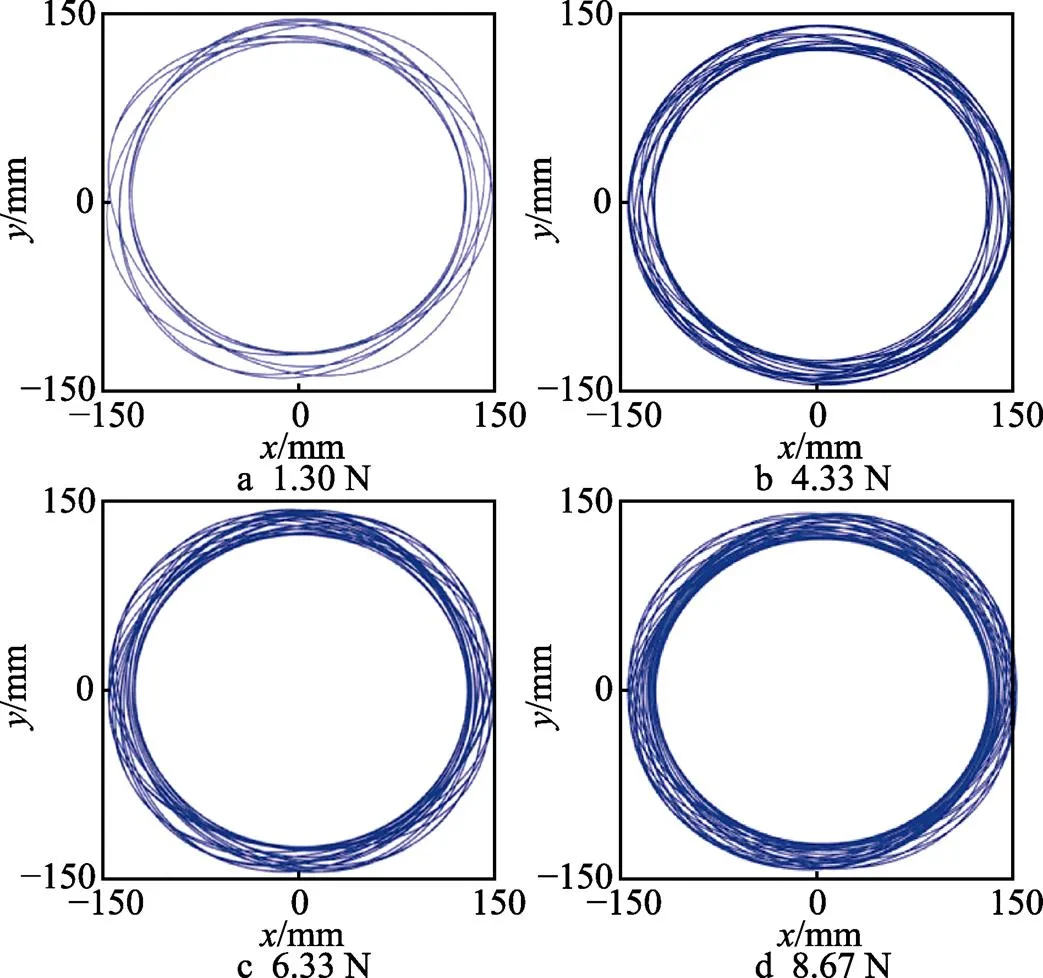
图7 改变研磨装置载荷的研磨轨迹

当研磨装置施加载荷为1.30 N时，研磨轨迹呈现稀疏状态，形状较不规整。继续增大研磨装置的施加载荷，在载荷为4.33 N时，研磨轨迹密集程度得到提升。继续将载荷增至6.33 N，研磨轨迹变密集的程度趋于稳定。当载荷达到8.67 N时，陶瓷球研磨轨迹趋于均匀。说明随着研磨装置施加载荷的增加，陶瓷球的研磨轨迹趋于密集。这种现象出现的原因是载荷的增加，在陶瓷球研磨过程中受到载荷作用球体上产生的速度1变大，球体的运动速度增加，在相同加工周期内形成的研磨轨迹则变得密集。

第3组仿真设定磨粒的粒径为自变量，分别取4组磨粒型号（W7、W10、W20、W30）为实验对象。经分析可知，当研磨过程中的转速g=50 r/min、施加载荷N=1.30 N、自转角=45°时，分别改变磨粒的型号（尺寸），得到的仿真研磨轨迹如图8所示。

图8 改变磨粒型号的研磨轨迹

由图8可知，当磨粒的型号为W7时，研磨轨迹的密集程度较低，每条轨迹的交互性较差。更换不同型号的磨料，以增大磨粒的粒径。当磨料型号为W10时，单位区域内的研磨轨迹线数量明显增加。接着更换磨料为W20，研磨轨迹的数量进一步增加。当型号更替为W30时，轨迹的数量开始趋于稳定，变化幅度和变化范围均减小。说明随着磨料型号的变化、粒径的增加，陶瓷球的研磨轨迹数量随之增加，单位区域内的轨迹密度得到提升。这种现象出现的原因是磨粒粒径的增大，磨粒作用在球体表面上的载荷L也相应增加，在研磨过程中对球体产生的速度2也随之提升，球体与下研磨盘的接触频率上升，则形成的研磨轨迹线数量增加。

3 研磨参数对氮化硅陶瓷球表面质量的影响规律

由上述仿真结果可知，氮化硅陶瓷球在研磨过程中受到研磨盘的转速g、施加的载荷N、磨粒粒径g的影响。为了验证仿真结果，同时进一步揭示不同研磨轨迹下研磨参数对陶瓷球表面研磨质量的影响机制，现利用锥形研磨盘对氮化硅陶瓷球进行实验研究。

3.1 实验条件

采用立式研磨机，型号为TS−5000，该研磨机的结构如图9所示，上下研磨盘直径均为320 mm，研磨盘转速范围设定为50～200 r/min。选用粗磨后的热等静压氮化硅陶瓷球为实验对象，毛坯球的粗糙度在0.49～0.63 μm范围内浮动，在同一批次里取4个样品用千分尺取4个点测量球体的直径，如表1所示。设定单颗陶瓷球承受的研磨压力为1～9 N，采用的研磨液基液以煤油为主、以机油为辅，在研磨过程中使用磨粒尺寸为W7到W30的金刚石磨粒，每组实验初步设定使用毛坯球30颗，每组实验时间为10 h。

图9 锥形研磨机及其结构示意图

表1 毛坯球部分尺寸

3.2 方案

为了研究研磨盘转速和研磨装置施加载荷，以及它们之间的交互作用，现采用三因素随机实验，分别确定每个因素的各个水平在另一因素不同水平上的变化趋势，避免多种因素混合叠加作用对实验结果产

生干扰。同时减少实验次数，以提高实验效率。

此次实验设置的因素和水平如表2所示。其中，三因素即磨粒粒径、研磨盘转速和研磨装置施加载荷，它们分别与各自对应的4个水平进行交叉实验，共计16组。

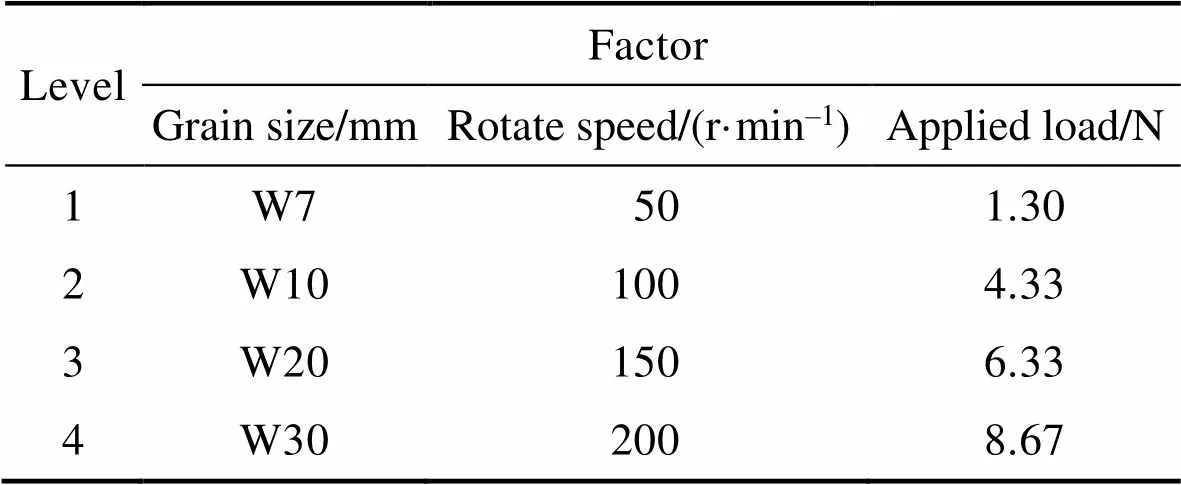
表2 实验因素和水平设置

采用实验室中的泰勒接触式surtronic25型粗糙度仪测量陶瓷球的表面粗糙度，在测量前对装置进行标定，以避免观测结果出现球面曲率过大的现象。分别对陶瓷球表面均匀分布的6个点进行测量，将其平均值作为其粗糙度。将实验得到的氮化硅陶瓷球通过VHX−1000E超景深三维显微镜和HITACHIS−4800扫描电镜观察分析其表面形貌。

4 结果与分析

4.1 实验结果

以此次实验结果为依据，建立变量与期望值的对应关系，如表3所示。设定研磨盘转速为变量，研磨盘装置施加载荷为变量，实验中使用的磨粒型号为，实验测得的陶瓷球表面粗糙度值为期望值()。由表3可知，实验可以类比为三因素四水平的正交实验，依据实验结果建立不同研磨参数在不同水平下的表面粗糙度的变化趋势，表3中分别为磨粒粒直径、转速、载荷对应的水平量，(,,)为相应水平量下的期望值()，具体如图10所示。

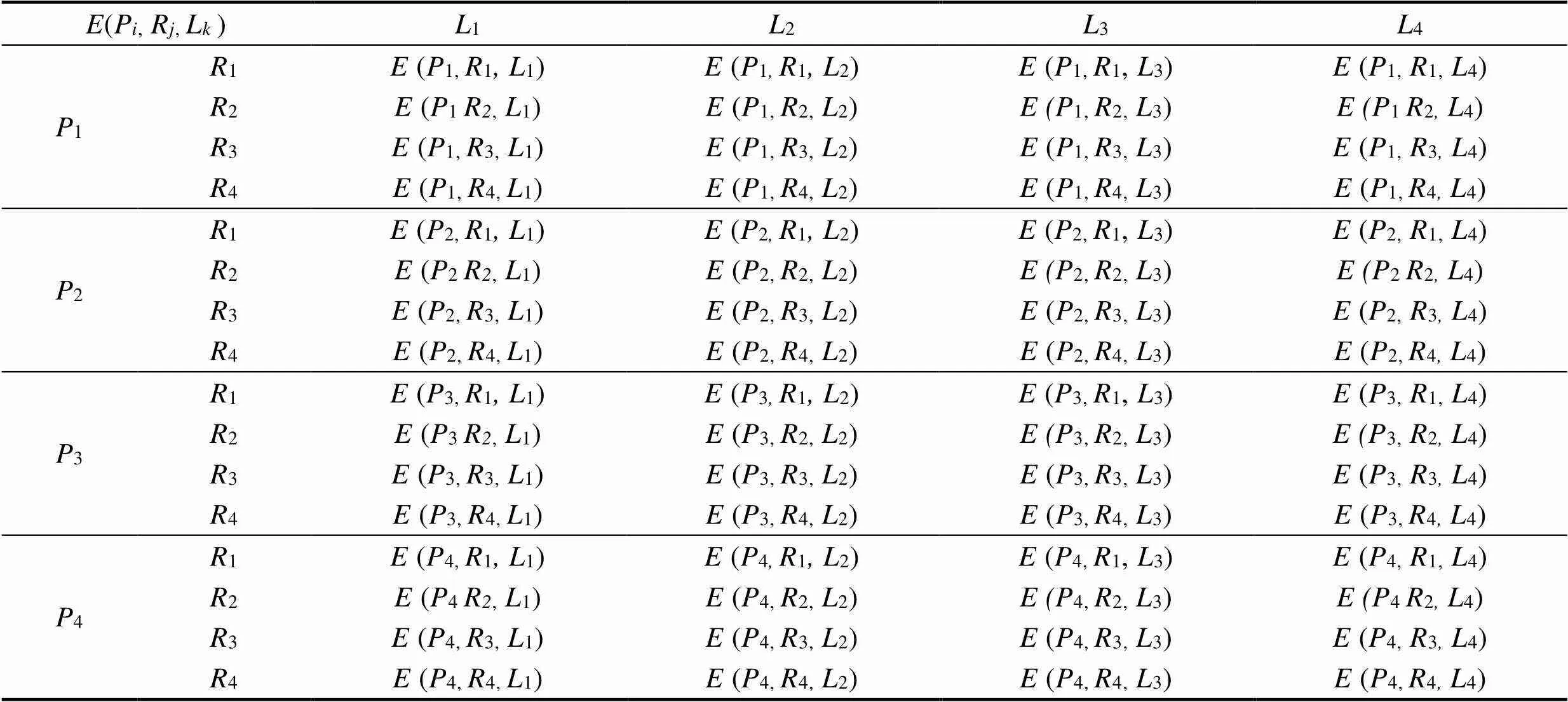
表3 L、R、P与E(Ra)的对应关系

图10 Ra变化趋势

分析图10a可知，研磨盘转速与陶瓷球表面粗糙度值成正比，随着研磨盘转速由低转速状态变化到高转速状态，即由50 r/min变化至200 r/min时，陶瓷球的表面粗糙度变化明显。分析图10b可知，当施加的载荷较低时，表面粗糙度值偏低，表面质量较好。随着载荷的增加，尤其是在区间4.33～8.67 N内，表面粗糙度不断增大，表面质量逐渐变差。分析图10c可知，增大参与研磨的磨粒粒径，其表面粗糙度上升，表面质量变差。当磨粒型号取W10以上时，其表面粗糙度开始递增，球体表面质量持续下降。

4.2 实验分析

此次实验分为4组，分别在W7、W10、W20、W30型号磨粒下进行，以不同转速在同一载荷变化范围内的表面粗糙度为实验对象，探讨各个研磨参数对陶瓷球表面质量的影响。实验得到的陶瓷球表面粗糙度变化规律如图11所示。

在相同磨粒、载荷条件下，转速对表面质量的变化规律基本接近。如图11a所示，在W7磨粒条件下。随着研磨盘转速的降低，磨粒参与研磨的时间变长，陶瓷球表面开始与磨粒充分接触，研磨盘与单颗陶瓷球之间的磨粒浓度变大，陶瓷球与研磨盘之间参与研磨的磨粒量变多，作用在每个磨粒上的法向力减小，陶瓷球表面开始由滑动磨损转变为滚动磨损，从而使陶瓷球的表面粗糙度降低[27]，球体表面质量变好。

在相同磨粒、转速条件下，载荷对表面质量的影响效果大体相同。如图11a所示，在W7磨粒条件下，随着载荷从8.67 N减小至1.30 N，不同转速下测得的球体表面粗糙度均呈下降趋势。其中，在50 r/min下的粗糙度由0.051 7 μm降至0.009 6 μm，载荷和表面粗糙度呈正相关。在不同载荷下测得的球体表面粗糙度均呈上升趋势。其中，在8.67 N条件下的表面粗糙度由0.091 2 μm上升至0.151 μm，转速和粗糙度成正比。在增大研磨装置施加载荷时，处于陶瓷球与研磨盘接触部分的单颗磨粒所承受的约束也随之增加，嵌入研磨盘内部的磨粒浓度上升，磨粒以刻划的方式较深地切入陶瓷球表面，研磨后的陶瓷球表面质量下降[28]。

对比图11a—d可知，选择不同的磨粒型号，在相同转速和载荷条件下得到的球体表面粗糙度差异较大。如图11a所示，当选用粒径较小的磨粒型号W7时，陶瓷球在50 r/min的转速和1.30 N载荷下得到的最小粗糙度为0.009 6 μm。由图11d可知，当选用粒径较大的磨粒型号W30时，陶瓷球在相同研磨条件下得到的最大粗糙度为0.133 1 μm。即减小磨粒粒径，球体的表面粗糙度也相应减小。磨粒粒径的减小在一定程度上不仅能够增加被加工球体单位面积内的磨粒数量，还能提升研磨过程中有效切削磨粒的数量在整体磨粒数量中的比例，使球体在加工中充分受到来自磨粒的切削作用，表面质量变好。

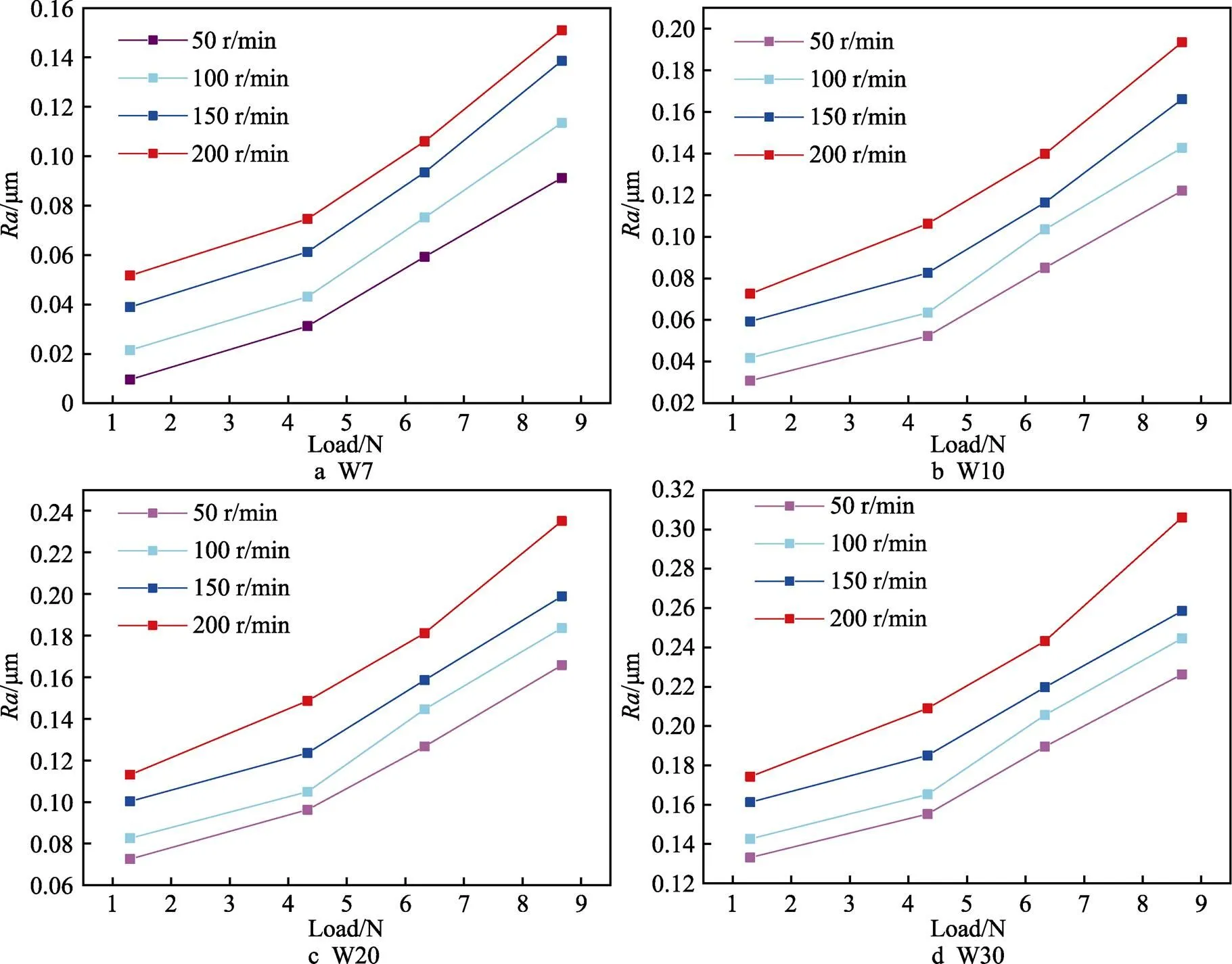
图11 各个型号磨粒下不同转速在相同载荷变化范围内的表面粗糙度变化趋势

4.3 研磨参数对陶瓷球表面形貌的影响

实验采用热等静压氮化硅陶瓷球，将上述实验的毛坯球进行取样分析，通过观察可知，毛坯表面质量较差，球体表面存在明显的烧结和缺陷，如图12a所示。为了探究不同轨迹下的研磨参数对陶瓷球表面质量的影响，现对研磨后的球体表面进行去除机理分析。

利用VHX−1000E超景深三维显微镜和HITACHIS− 4800扫描电镜对实验后的陶瓷球表面进行观察，分析不同研磨参数对陶瓷球表面质量的影响。在对陶瓷球表面进行研磨的过程中，更改磨粒的型号（粒径），球体表面的质量呈现不同的状态。由图13可知，当采用W30型号磨粒进行研磨加工时，球体表面划痕较深，表面质量较差。由图14可知，当更换磨粒型号为W7时，表面划痕由深变浅，表面质量得到改善。

陶瓷球在研磨加工时的材料去除方式主要有二体断裂去除和三体脆形断裂去除。相关文献指出，当二体断裂去除方式在材料去除方式中所占比例增加，材料的表面质量变差[29]。增大研磨装置施加的载荷，磨粒被逐步挤压进入陶瓷球表面，从而产生了裂纹。随着载荷的增加，陶瓷球表面的裂纹持续延伸，最终从表面剥落，形成凹坑。研磨装置对磨粒的挤压作用加剧，磨粒被逐渐切入工件表面，进行滑动运动，从而在陶瓷球表面划擦，形成划痕。如图13d和图15a所示，可以明显观察到磨粒划擦后陶瓷球加工表面产生的凹坑和划痕。此时材料去除方式中二体断裂去除的比例较高，研磨得到的陶瓷球表面质量较差，故在图13a所示工艺条件下加工得到的表面质量较好。同理，随着研磨盘转速的减小，研磨液中的金刚石磨料趋于均匀分布于陶瓷球表面，在陶瓷球和研磨盘的接触区域内参与研磨的单颗磨粒受到的载荷减小，受到的约束变少，陶瓷球表面与磨粒的相互作用更加充分。如图14a—d和图15b所示，陶瓷球表面划伤和雪花状缺陷减少，但表面产生的微小断裂裂纹增多。此时，材料去除方式中三体脆形断裂去除所占的比例上升，研磨得到的陶瓷球表面质量较好，故在图15a所示研磨参数下得到的表面质量较高。

图12 陶瓷球毛坯表面形貌

Fig.12Surface morphology of ceramic ball blank: a)surface defects of blank ball; b) three-dimensional morphology of defects

图13 W30磨粒下载荷变化的陶瓷球表面超景深图

图14 W7磨粒下转速变化的陶瓷球表面超景深图

图15 表面缺陷SEM图

对比图13、14中加工后的表面形貌和图12中初始毛坯球的表面形貌可知，研磨盘转速、研磨装置施加载荷、磨粒粒径对陶瓷球表面质量有着重要的影响。减小转速、载荷、粒径能够得到良好的表面质量。相反增加转速、载荷、粒径，则会得到较差的表面质量。

4.4 实验与仿真分析

在陶瓷球的研磨过程中，通过降低研磨盘的转速，陶瓷球的研磨轨迹趋于稀疏，在单位时间内参与研磨的磨粒数量增加，磨粒浓度上升。此时，陶瓷球的表面粗糙度下降，材料去除方式主要以三体脆性断裂去除为主，陶瓷球表面的划伤和凹坑较少，细小裂纹较多，表面质量较好。

增大研磨装置的施加载荷，陶瓷球研磨轨迹的密集度上升。这表明磨粒受到的约束变大，磨粒的运动方式由滚动转变为滑动运动。此时陶瓷球的表面粗糙度上升，材料去除方式以二体断裂去除为主，表面划伤和凹坑较多，表面质量较差。

5 结论

1）根据氮化硅陶瓷球在锥形研磨法研磨过程中轨迹的变化，建立了陶瓷球研磨轨迹的数学模型。基于此进行了仿真及实验，分析可知陶瓷球在研磨过程中会受到磨粒粒径g、研磨盘转速g、研磨装置施加在陶瓷球上的载荷N的共同影响。

2）在研磨的过程中，磨粒粒径g研磨装置施加在陶瓷球上的载荷N和研磨盘转速g越小，研磨轨迹越稀疏。此时以三体脆性断裂去除为主，陶瓷球表面的划伤和凹坑较少，微小裂纹较多，表面质量较好。反之，磨粒粒径g载荷N和转速越大，研磨轨迹的密集程度越高。此时以二体断裂去除为主，陶瓷球表面的划伤和凹坑较多，表面质量较差。

3）采用降低研磨盘转速g、减少研磨装置施加载荷N使用较小磨粒型号的研磨方法，能够使研磨后的陶瓷球表面粗糙度降低，表面缺陷变少，表面质量变好。

[1] SHI Huai-tao, BAI Xiao-tian, ZHANG Ke, et al. Influence of Uneven Loading Condition on the Sound Radiation of Starved Lubricated Full Ceramic Ball Bearings[J]. Journal of Sound and Vibration, 2019, 461(C): 114910-114910.

[2] 吴承伟, 张伟, 李东炬. 超精密高性能氮化硅轴承研究现状与应用[J]. 精密制造与自动化, 2020(1): 1-3.

WU Cheng-wei, ZHANG Wei, LI Dong-ju. Current Situation and Application of Research on Super-Precision High-Per­for­mance Silicon Nitride Bearings[J]. Precise Manufac­turing & Automation, 2020(1): 1-3.

[3] TAM H Y, CHENG H B, WANG Y W. Removal Rate and Surface Roughness in the Lapping and Polishing of RB-SiC Optical Components[J]. Journal of Materials Pro­ces­sing Technology, 2007, 192/193: 276-280.

[4] LIANG Xiao-hu, LIN Bin, LIU Xue-lian. Analysis of Local Features of Engineering Ceramics Grinding Surface[J]. Measurement, 2020, 151: 107205.

[5] SHI H T, BAI X T. Model-Based Uneven Loading Con­dition Monitoring of Full Ceramic Ball Bearings in Starved Lubrication[J]. Mechanical Systems and Signal Processing, 2020, 139: 106583.

[6] MA Shuai-jun, ZHANG Xiao-hong, YAN Ke, et al. A Study on Bearing Dynamic Features under the Condition of Multiball–Cage Collision[J]. Lubricants, 2022, 10(1): 9.

[7] BARAHENI M, AMINI S. Predicting Subsurface Damage in Silicon Nitride Ceramics Subjected to Rotary Ultra­sonic Assisted Face Grinding[J]. Ceramics International, 2019, 45(8): 10086-10096.

[8] 周芬芬, 袁巨龙, 赵萍, 等. 氮化硅陶瓷球材料性能参数测试及其相关性分析研究[J]. 机电工程, 2016, 33(6): 689-693.

ZHOU Fen-fen, YUAN Ju-long, ZHAO Ping, et al. Test and Correlation Analysis on Material Performance Para­meters of Silicon Nitride Ceramic Ball[J]. Journal of Me­cha­nical & Electrical Engineering, 2016, 33(6): 689-693.

[9] 张珂, 王定文, 李颂华, 等. 氮化硅陶瓷球研磨去除机制试验与仿真研究[J]. 润滑与密封, 2020, 45(7): 16-22.

ZHANG Ke, WANG Ding-wen, LI Song-hua, et al. Ex­peri­ment and Simulation Study on the Material Removal Mode of Si3N4 Ceramic Balls in Lapping Process[J]. Lubrication Engineering, 2020, 45(7): 16-22.

[10] ZHANG Ke, SUN Jian, WANG He, et al. Experimental Research on High Speed Grinding of Silicon Nitride Ceramic Spindle[J]. Materials Science Forum, 2016, 874: 253-258.

[11] KUMAR A, GHOSH S, ARAVINDAN S. Experimental Investigations on Surface Grinding of Silicon Nitride Subjected to Mono and Hybrid Nanofluids[J]. Ceramics International, 2019, 45(14): 17447-17466.

[12] 周芬芬, 袁巨龙, 姚蔚峰, 等. 精密球超精密加工技术的研究进展[J]. 中国机械工程, 2019, 30(13): 1528-1539.

ZHOU Fen-fen, YUAN Ju-long, YAO Wei-feng, et al. Review on Ultra-Precision Machining Technology of Precision Balls[J]. China Mechanical Engineering, 2019, 30(13): 1528-1539.

[13] ZHANG Xiao-hong, ZHANG Zhi-cheng, DENG Zhao-hui, et al. Precision Grinding of Silicon Nitride Ceramic with Laser Macro-Structured Diamond Wheels[J]. Optics & Laser Technology, 2019, 109: 418-428.

[14] ZHANG X H, WEN D, DENG Z H, et al. Study on the Grinding Behavior of Laser-Structured Grinding in Silicon Nitride Ceramic[J].The International Journal of Advanced Manufacturing Technology, 2018, 96(9-12): 3081-3091.

[15] 吴玉厚, 王浩, 孙健, 等. 氮化硅陶瓷磨削表面质量的建模与预测[J]. 表面技术, 2020, 49(3): 281-289.

WU Yu-hou, WANG Hao, SUN Jian, et al. Modeling and Prediction of Surface Quality of Silicon Nitride Ceramic Grinding[J]. Surface Technology, 2020, 49(3): 281-289.

[16] SUN Jian, WU Yu-hou, ZHOU Peng, et al. Simulation and Experimental Research on Si3N4 Ceramic Grinding Based on Different Diamond Grains[J]. Advances in Me­chanical Engineering, 2017, 9(6): 168781401770559.

[17] 吴玉厚, 王浩, 李颂华, 等. 氮化硅陶瓷磨削热特性与表面成形机制[J]. 表面技术, 2019, 48(12): 360-368.

WU Yu-hou, WANG Hao, LI Song-hua, et al. Grinding Thermal Characteristics and Surface Forming Mechanism of Silicon Nitride Ceramics[J]. Surface Technology, 2019, 48(12): 360-368.

[18] 吴玉厚, 王维东, 李颂华, 等. 干湿磨条件下氧化锆陶瓷表面粗糙度实验[J]. 沈阳建筑大学学报(自然科学版), 2017, 33(6): 1080-1087.

WU Yu-hou, WANG Wei-dong, LI Song-hua, et al. Experiments of Surface Roughness of Zirconia Ceramics under Wet and Dry Grinding[J]. Journal of Shenyang Jian­zhu University (Natural Science), 2017, 33(6): 1080-1087.

[19] 袁巨龙, 项震, 吕冰海, 等. 变曲率沟槽高精度球体精研工艺优化实验研究[J]. 浙江工业大学学报, 2019, 47(2): 140-145.

YUAN Ju-long, XIANG Zhen, LYU Bing-hai, et al. Research on Optimization Experiment for Precision Balls with Variable-Radius Groove in Finishing Process[J]. Journal of Zhejiang University of Technology, 2019, 47(2): 140-145.

[20] 王旭, 赵萍, 吕冰海, 等. 滚动轴承工作表面超精密加工技术研究现状[J]. 中国机械工程, 2019, 30(11): 1301- 1309.

WANG Xu, ZHAO Ping, LYU Bing-hai, et al. Research Status of Ultra-Precision Machining Technologies for Wor­king Surfaces of Rolling Bearings[J]. China Mechani­cal Engineering, 2019, 30(11): 1301-1309.

[21] 郭伟刚, 袁巨龙, 周芬芬, 等. 基于偏心式变曲率沟槽的高精度球体加工理论与试验研究[J]. 机械工程学报, 2019, 55(9): 183-190.GUO Wei-gang, YUAN Ju-long, ZHOU Fen-fen, et al. Theoretical and Experimental Research on Processing Balls with Eccentric Variable-Radius V-Groove[J]. Journal of Mechanical Engineering, 2019, 55(9): 183-190.

[22] 李颂华, 李雪, 吴玉厚. 全陶瓷主轴–轴承单元的动力学研究[J]. 沈阳建筑大学学报(自然科学版), 2015, 31(1): 140-148.

LI Song-hua, LI Xue, WU Yu-hou. Dynamic Research on the Full-Ceramic Spindle-Bearing Unit[J]. Journal of Shenyang Jianzhu University (Natural Science), 2015, 31(1): 140-148.

[23] 马志飞, 梁国星, 张昊, 等. 单颗磨粒高速磨削Ti6Al4V仿真与试验验证[J]. 工具技术, 2019, 53(4): 49-53.

MA Zhi-fei, LIANG Guo-xing, ZHANG Hao, et al. Simulation and Experimental Investigation of High-Speed Grinding Ti6Al4V with Single Grain[J]. Tool Engineering, 2019, 53(4): 49-53.

[24] 杨军, 李志鹏, 李伟, 等. 基于不同单颗磨粒模型的微细磨削力研究[J]. 湖南大学学报(自然科学版), 2018, 45(8): 54-62.

YANG Jun, LI Zhi-peng, LI Wei, et al. Study on Micro- Grinding Force Based on Different Single Abrasive Particle Models[J]. Journal of Hunan University (Natural Sciences), 2018, 45(8): 54-62.

[25] 肖燏婷, 吴晓峰, 蔡姚杰, 等. 无理偏摆式平面研磨加工均匀性的数值模拟[J]. 机械工程学报, 2021, 57(13): 232-241.

XIAO Yu-ting, WU Xiao-feng, CAI Yao-jie, et al. Nu­merical Simulation on Uniformity of Plane Lapping with Irrational Swinging Method[J]. Journal of Mechanical Engineering, 2021, 57(13): 232-241.

[26] 李颂华, 韩涛, 孙健, 等. HIPSN陶瓷高效精密磨削工艺优化试验研究[J]. 表面技术, 2018, 47(9): 287-295.

LI Song-hua, HAN Tao, SUN Jian, et al. Optimization Experiment on HIPSN Ceramic High Efficient and Preci­sion Grinding Process[J]. Surface Technology, 2018, 47(9): 287-295.

[27] 李颂华, 王科冲, 孙健. 磨削加工中顺逆磨研究现状与发展[J]. 兵器材料科学与工程, 2021, 44(1): 111-119.

LI Song-hua, WANG Ke-chong, SUN Jian. Research Status and Development of Grinding Process under down and up Grinding[J]. Ordnance Material Science and Engineering, 2021, 44(1): 111-119.

[28] FENG Guang, GUO Ji-bao, ZHANG Guo-jun. Material Removal Characteristics of Ultra-Precision Grinding Silicon Carbide Ceramics[J]. Advances in Applied Ceramics, 2020,119(4): 175-182.

[29] 张珂, 王定文, 李颂华, 等. 氮化硅陶瓷球研磨去除方式[J]. 金刚石与磨料磨具工程, 2019, 39(3): 38-44.

ZHANG Ke, WANG Ding-wen, LI Song-hua, et al. Material Removal Mode of Lapping Si3N4Balls[J]. Diamond & Abrasives Engineering, 2019, 39(3): 38-44.

Analysis on Lapping Trajectory of Si3N4Ceramic Ball and Its Effect Mechanism for Surface Quality

a,a,a,a,b,a,b

(a. School of Mechanical Engineering, b. National-Local Joint Engineering Laboratory of NC Machining Equipment and Technology of High-Grade Stone, Shenyang Jianzhu University, Shenyang 110168, China)

As an important factor reflecting the surface shape accuracy of the sphere, the motion trajectory during the lapping process of the sphere has not been introduced and analyzed in the current research. For the above reasons, the lapping trajectory of the ceramic ball is introduced into the process of studying the effect mechanism of the surface quality of the sphere, which can be more accurate. The work aims to analyze the effect of lapping trajectory on the surface quality of the ceramic ball under the same lapping liquid ratio and abrasive type, but the different lapping disc rotation speed, load applied by the lapping device and abrasive particle, and clarify the optimal lapping parameters of silicon nitride ceramic ball processed by taper lapping, so as to improve the surface quality of the ceramic ball. Through the optimal lapping parameters, a silicon ceramic ball with good surface quality and high precision can be fabricated. Firstly, the relative motion model between the taper lapping disc and the silicon nitride ceramic ball was established during the lapping. On the basis of the established model, MATLAB was used to simulate the lapping trajectories of the silicon nitride ceramic ball under different lapping parameters. By analyzing these lapping trajectories, the effect of the lapping parameters on the motion state during the lapping process of the ball was obtained. Then, the taper lapping device was used for single-factor experiment verification, and the three variables involved in the experiment were set as the type of abrasive particles (particle size), the lapping disc rotation speed and the load applied by the lapping device. The experimental results were sampled, the surface roughness of the ball was measured by roughness meter, and the surface morphology of the lapping ceramic ball was detected by scanning electron microscope and ultra-depth three-dimensional microscope. Combined with the simulation analysis and experimental results, the effects of the lapping disc rotation speed, the load applied by the lapping device, and the size of the abrasive particles on the surface quality of the ball after processing were investigated. Combining the variation laws of lapping parameters obtained under different simulated lapping trajectories with the experimental results, the optimal lapping parameters obtained were: when the lapping disc rotation speed was 50 r/min, the applied load was 1.30 N and the abrasive particle type was W7, the surface roughness value of the ceramic ball obtained by processing was 0.009 6 μm, which basically met the quality requirements of G3-grade precision full-ceramic ball in actual production. The surface quality of the ceramic ball is greatly affected by the rotation speed of the lapping disc, the load applied by the lapping device and the size of the abrasive particles. With the decrease of the rotation speed of the lapping disc and the decrease of the load and the size of the abrasive particles, the lapping trajectory of the ceramic ball tends to be sparse, and the surface roughness shows a downward trend. Lapping silicon nitride ceramic ball by abrasive particles with smaller diameter at a lower rotation speed of the lapping disc and a smaller load applied by the lapping device is beneficial to improving the surface quality. The research results have important guiding significance for improving the surface quality of ceramic ball.

silicon nitride ceramic ball; taper lapping; lapping parameters; lapping trajectory; single-factor experiment; surface quality

TQ174.75

A

1001-3660(2023)01-0253-13

10.16490/j.cnki.issn.1001-3660.2023.01.026

2021–11–22；

2022–04–19

2021-11-22；

2022-04-19

国家自然科学基金（52105196）；辽宁省教育厅资助项目（LJKMZ20220936）；沈阳市中青年科技创新人才支持计划（RC210343）

National Natural Science Foundation of China (52105196); Program Funded by Liaoning Province Education Administration (LJKMZ20220936);Young and Middle-aged Scientific and Technological Innovation Talents in Shenyang Program (RC210343)

孙健（1986—），男，博士，副教授，主要研究方向为精密与超精密加工技术。

SUN Jian (1986-), Male, Doctor, Associate professor, Research focus: precision and ultra­precision machining technology.

田军兴（1987—），男，硕士，讲师，主要研究方向为精密与超精密加工技术。

TIAN Jun-xing (1987-), Male, Master, Lecturer, Research focus: precision and ultra­precision machining technology.

孙健, 陈伟, 姚金梅, 等. Si3N4陶瓷球研磨轨迹分析及其对表面质量的影响机制[J]. 表面技术, 2023, 52(1): 253-265.

SUN Jiana, CHEN Wei, YAO Jin-mei, et al. Analysis on Lapping Trajectory of Si3N4Ceramic Ball and Its Effect Mechanism for Surface Quality[J]. Surface Technology, 2023, 52(1): 253-265.

责任编辑：彭颋